干热岩热能重力热管采热系统数值模拟研究与经济性分析

黄文博，曹文炅，李庭樑，4，蒋方明

（1 中国科学院广州能源研究所先进能源系统研究室，广东广州510640； 2 中国科学院可再生能源重点实验室，广东广州510640； 3 广东省新能源和可再生能源研究开发与应用重点实验室，广东广州510640； 4 中国科学院大学，北京100049）

引 言

储量丰富的干热岩型地热资源是近年来国内外地热能开发利用研究的重点[1]。但是，作为目前开采干热岩的主流方式，增强型地热系统（enhanced geothermal system, EGS）却存在循环工质损失大、管道结垢腐蚀严重、井下连通困难和投资成本过高且风险大等问题[2]。

在这个背景下，一些研究者开始考虑采用井下换热器（downhole heat exchanger，DHE）系统来开采干热岩地热能。DHE 系统通过在地热井中设置一个由U 形管或套管组成循环系统，进而利用流体工质在管内的流动持续从井中开采热能。由于DHE系统的流体工质循环过程完全封闭，从根本上杜绝了管道的腐蚀和结垢，以及工质损失等问题。并且DHE 系统为单井采热，无须进行井下连通，可以很方便地建立在废弃的石油和天然气井口，从而大幅减少了钻井费用，降低项目投资风险。一些研究者已经对使用DHE 系统来开采干热岩热能的方案展开了实验和理论研究[3-8]。例如，Kohl 等[4]研究了置于一个深度为2302 m 的废弃油井中的井下换热器地热的采热性能，运行过程中其采热功率受到循环流量的影响，在40～200 kW 范围变化。Bu 等[6]对井下换热器的运行过程进行了模拟计算，结果表明当地温梯度为45℃/km，深度为4000 m 时，井下换热器的采热量可达800 kW，净发电量可达52 kW。Nian等[9]计算了一个深度为3000 m，井底温度为126℃的井下换热器系统采热性能；如果该系统在一年只运行3 个月的情况下，其产热功率可以达到700 kW。可以看出DHE 的单井采热量往往较低，通常都在1 MW以下，发电量在50 kW左右。

近期，Huang 等[10]提出将人工裂隙热储与单井重力热管采热相结合的技术方案，为干热岩单井式地热系统提供了另一种思路。以浅层地热系统的工程经验来看，地热井附近可渗透介质中的地下水流动[11-12]和自然对流作用[13-14]可以显著增加DHE 系统的采热性能。而热储与井下换热器的平均换热温差是影响热储中自然对流强度的关键因素[15]。采用U 形管或套管的单相流DHE 系统将地热能以显热的形式储存在循环工质中，当循环工质吸收地热能之后工质温度也会随之上升，难以在热储和井下换热器之间形成较大温差，限制了热储中的自然对流强度。而重力热管利用管内工质在重力作用下由液气相变而产生的自然对流效应，可将热量迅速地从高温端传输到低温端。同时，由于重力热管将热能储存在工质潜热中，其工质温度不会随着热量的吸收而增长，因此重力热管能够在采热过程中维持更高的传热温差，进而可以更充分地利用裂隙热储中的自然对流效应来强化系统的采热性能。

为了论证干热岩重力热管地热系统的技术经济性。本文将重力热管内部热质传递过程与干热岩热储内热流过程模型相结合，建立了干热岩重力热管地热系统数值模型。基于该模型，本文模拟了干热岩重力热管地热系统的长期运行过程，评估该系统的供热和发电潜力，并据此计算了重力热管地热系统的成本电价，还进一步将其与EGS和DHE 地热电站的成本电价进行了比较。研究成果将为重力热管在地热开发中的应用提供理论基础。

1 物理-数值模型

1.1 物理模型

在重力热管式干热岩采热系统运行过程中，热管管壁的温度变化会对热储中传热过程产生影响，尤其当热管周围存在可渗透的裂隙热储时，热管的温度会直接影响到裂隙热储中的自然对流强度；热储温度的变化也会使热管吸热量发生改变，进而对热管内部的气液两相流动传热过程产生影响。准确评估重力热管干热岩采热系统的运行过程，需要考虑热储中的渗流传热过程与热管内部气液两相流动传热过程的耦合作用。

图1 重力热管地热系统（a）与套管式井下换热器系统（b）模型示意图Fig.1 Schematic diagram of heat pipe(a)and downhole heat exchanger(b)geothermal system

图1 显示了研究所采用的系统模型。该模型将地下岩体区域视为多孔介质，通过设置不同的渗透率及孔隙率将地下岩体划分为不可渗透岩石和裂隙热储；对于热管内部气液两相流动传热过程，本研究将热管简化为一维模型，只考虑物理量在热管轴向上的变化，并将热管以变温边界的形式导入地下岩体区域的数值模型中，实现了热管内部过程与管外过程的耦合求解。进一步，本文还基于以上物理模型，模拟了套管式井下换热器地热系统的运行过程，并将其与重力热管地热系统进行了比较。

1.2 地下岩体数学模型

针对热储及岩石中的渗流和传热过程，本文采用了之前开发的裂隙热储热流耦合过程数值真模型[16-18]。该模型基于局部非热平衡思想，采用两个能量方程来分别描述裂隙热储中流体和岩石的温度场，可更加真实地还原采热过程中岩石-流体的换热过程。该模型已经多次应用于EGS 采热过程的数值仿真研究中[16-18]，并且Cao 等[19]还在该模型的基础上进一步考虑了温度、压力对热储中流体工质密度、黏度和比热容等物性参数的影响，可以对热储中的自然对流过程进行模拟。该模型的基本假设如下：

（1）地下岩体视为多孔介质；

（2）热储中充满流体工质；

（3）流体工质为单相流动；

（4）忽略基岩和盖岩的渗透性，流体工质的损失量为零；

（5）不考虑循环流体与岩石的化学反应；

（6）忽略岩石热应变导致的热储孔隙率以及渗透率的变化。

在此基础上，模型求解的主要控制方程为：连续性方程

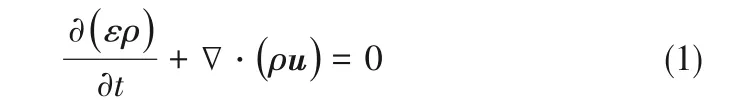
动量方程

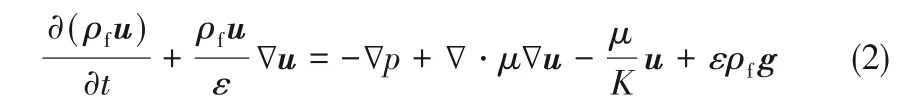
流体的能量方程

岩石的能量方程

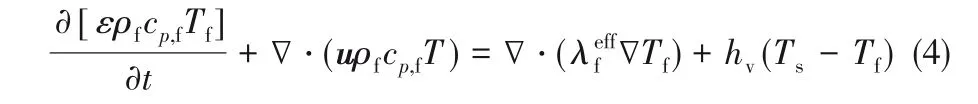
能量方程考虑了热储中的流体和岩石间的非热平衡现象，在一个等效体积单元内采用了两个能量方程来分别描述流体和岩石中能量平衡，同时采用牛顿冷却定律来描述流体和岩石之间的传热过程，认为其热流量等于温差和等效体积传热系数的乘积，hv表示该等效体积传热系数，该参数不仅与流体和岩石的物性有关，还与裂隙开度和等效体积单元内的裂隙数目有关，Jiang 等[16]给出了理想的平行裂隙模型下hv的计算方法。

1.3 单井采热数学模型

图1右侧虚线方框中显示了本次研究中使用的两种采热管道设计方案。

（1）重力热管开采方案。该方案管内为两相流，通过流体工质在重力作用下由气液相变而产生的自然对流，来实现热量的快速传递[图1(a)]。

（2）套管式地下换热器采热方案。管内为单相流，冷工质通过外侧环形槽道流入，工质吸收地热能温度升高之后从内管流出，从而实现地热能的持续开采[图1(b)]。

1.3.1 重力热管 重力热管通过管内气液相变形成的自然对流效应，实现热量自下往上的高效传输。而常规结构的重力热管受限于积液效应、气液卷携等问题，有效传输距离通常在100 m 以内。针对以上问题，研究者们提出了很多改进方案。Vasil'Ev[21]提出在重力热管内部设置液体回流管路用于避免气液卷携现象，使得超长重力热管在地热领域的应用成为可能。 Mashiko 等[22]进一步提出了在回液管侧壁设置多个喷嘴，通过喷淋的方式保持蒸发段内壁的润湿，进而避免蒸发段的积液问题。基于以上系统，Kusaba等[23]开展了较大型的示范性实验，热管总长为150 m，结果显示该系统能够以80℃的蒸汽温度输出90 kW 的采热量。Zhang 等[24]搭建了地热热管实验台，研究了设置内管和翅片结构，以及采用纳米流体对热管相变性能的影响。张龙等[25]对井深为3000 m 的超长重力热管进行了实验研究，实验中采用了金属网吸液芯和分流管等改进结构，在34.3℃的蒸汽温度下取得了174 kW 的传热量。可以看出，通过管内结构的改进能够在一定程度上避免常规重力热管存在的积液效应、气液卷携等问题。

本次研究中假设重力热管系统通过管内的结构优化能够实现如下性能：

（1）热管底部不存在积液，即在热管底部凝液流量与蒸汽流量都为0；

（2）管内无气液卷携作用，管内压力变化由蒸汽流动阻力决定，并且满足管道中湍流流阻的经验公式；

（3）管内处于相平衡状态；

（4）热管顶部为定温冷凝。

在此基础上，管内模型求解的主要控制方程如下：

连续性方程

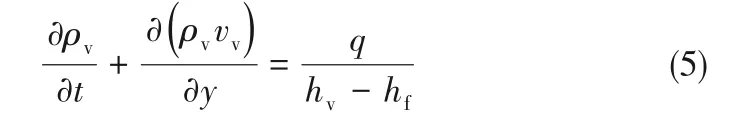
动量方程

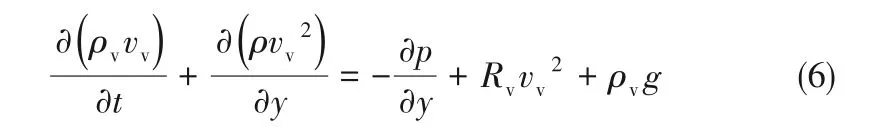
能量方程

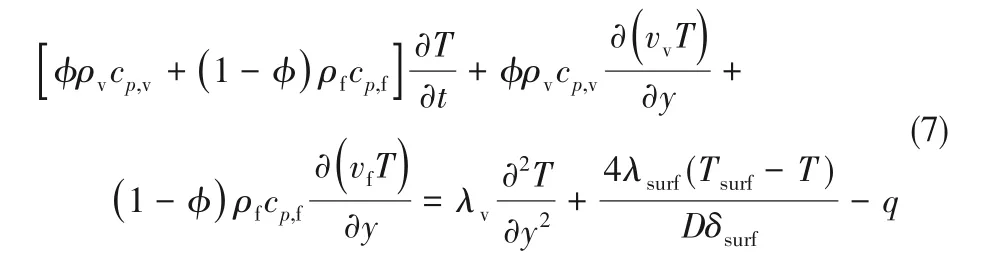
由于蒸汽质量的增加/减少量等于凝液质量的减少/增加量，并且假设在热管底部蒸汽流量与回液量都为0，可推知在管内任意横截面上蒸汽质量通量与凝液质量通量互为相反数：

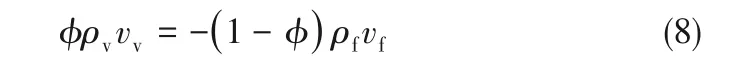
根据式(8)可以将能量方程式(7)简化为：

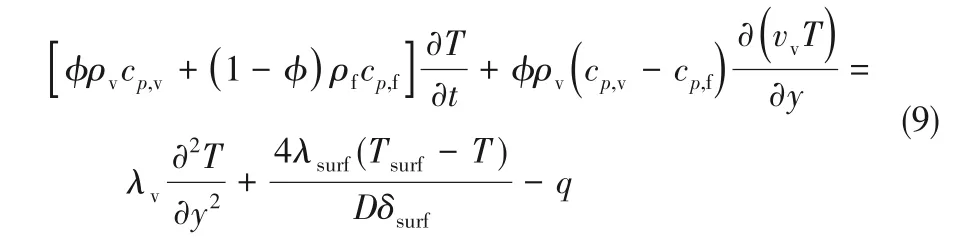
式中，v 表示速度在轴向上的分量；q 表示相变热量；下角标v和f分别表示气相和液相；φ表示气相体积分数；Tsurf、δsurf、λsurf分别表示管壁温度、厚度和热导率；式(6)中的流动阻力项根据假设（2）得来，其中Rv表示蒸汽流阻，可以根据Swamee 等[26]提出的管道流阻的经验公式进行计算：

式中，e表示管道粗糙度；D 表示管道当量直径；Re 表示流体Reynolds 数。式（10）适用于10-8＜e/D＜0.01，5000＜Re＜108。

式(5)、式(6)、式(9)为热管内部过程的控制方程，共包含vv、p、T、Tsurf、q 五个变量，为了使控制方程封闭需要加入两个额外方程。根据假设（3）可得管内的温度与压力满足工质的饱和温度-压力曲线：

管壁上的热通量qsurf满足：

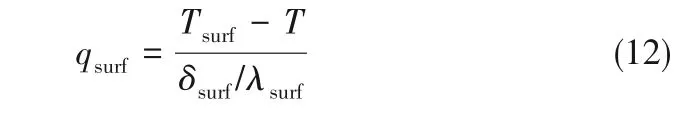
在计算过程中，qsurf从管外控制方程的求解中获得，然后用于求解管内方程；而管内方程求解完毕之后，可以得出管壁温度Tsurf，然后再以温度边界的形式用于求解管外控制方程。在计算过程中，管内方程中的qsurf和管外方程中的Tsurf每个迭代步都会进行一次修改，从而实现管内过程与管外过程的强耦合求解。

1.3.2 套管式地下换热器 对于套管式地下换热器，本次研究同样采用了一维简化模型，并对内、外管的温度进行区分，其控制方程如下：

质量方程

动量方程

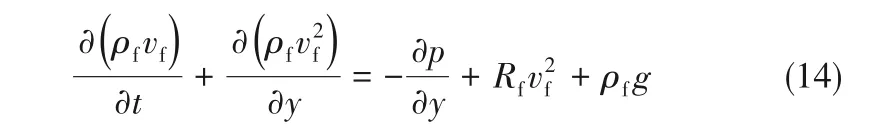
注入管（外管）的能量方程

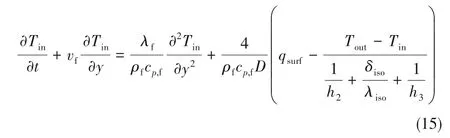
产出管（内管）的能量方程

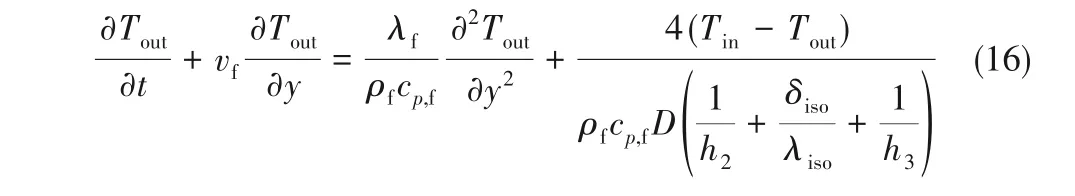
式中，ρiso、λiso分别表示保温管厚度和热导率；h2、h3分别为外管流体对内管壁、内管流体对内管壁的对流传热系数，其大小由充分发展的湍流管道中对流传热的无量纲经验公式计算得到：

式中，Pr表示流体工质的Prandtl数。

而管壁上的热通量qsurf满足：

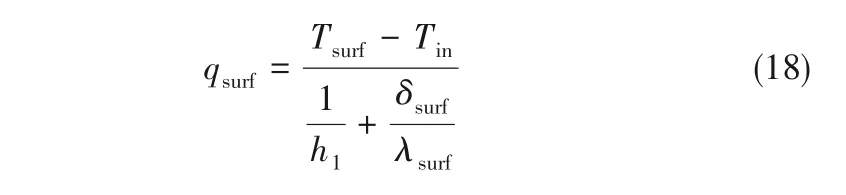
式中，h1为外管流体对外管壁的对流传热系数。与重力热管模式迭代方式相同，qsurf从管外控制方程的求解中获得，并用于求解管内方程，而管壁温度Tsurf能以温度边界的形式用于求解管外控制方程，通过迭代使控制方程收敛之后再进入下一个时间步。

1.4 参数设置

图2显示了本次研究中单井采热系统的几何模型。其中，采热管道直径为0.3 m，管长为4500 m。对于有热储的采热系统，设置热储为直径50 m 的圆柱体，其中心位于地下4000 m处，高度为1000 m，同时为了更好地利用热储中的自然对流作用，该系统还在管壁周围设置有宽度为0.1 m 的自然对流槽道。地下岩体区域的参数设置如下：地下岩石的密度为2650 kg/m3，比热容为1000 J/(K·kg)，热导率为2.1 W/(℃·m)，等效体积传热系数取为1 W/(K·m3)，该值参考文献[16,20]中使用的值；对于不可渗透岩石，其孔隙率和渗透率都为0；对于热储区域孔隙率为0.05，渗透率为10-12m2，并在比较算例中考虑了渗透率为10-11～10-14m2的情况；对于管体与井孔间的夹层区域，认为其孔隙率为0.15，渗透率为10-8m2，等效体积传热系数取为100 W/(K·m3)，以上参考Huang 等[10]研究中采用的参数；地表温度为30℃，地温梯度为0.045℃/m；计算过程中地表及计算区域底部都设为定温边界，其温度始终与初始温度相等，而计算区域侧边界则设置为绝热边界。

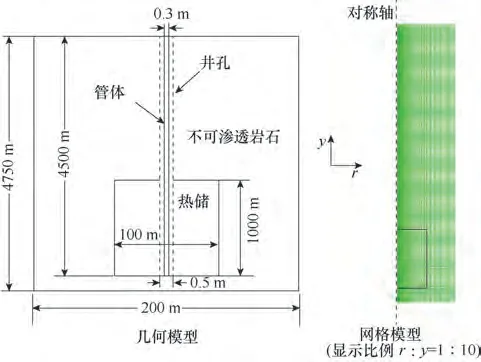
图2 几何与网格模型Fig.2 Geometric dimension and computational mesh

对于重力热管采热方案，本次研究中考虑管径为0.3 m的热管，管壁厚度为0.02 m，热导率为50 W/(℃·m)（参考碳钢物性）；管内工质采用水；热管顶端饱和温度为100℃；在周围岩石初始温度低于110℃的管道外壁，设有厚度为1 cm 热导率为0.025 W/(℃·m)的保温层。对于套管式采热方案，数值模型中考虑外管管径为0.3 m，内管管径为0.2 m的套管，管壁厚度均为0.01 m；内管设有厚度为1 cm 热导率为0.025 W/(℃·m)的保温层，流体工质由外管注入，内管流出；流体工质采用水，注入温度为30℃，循环流量为6 t/h(1.667 kg/s)；管壁粗糙度为0.1 mm。

热储中的流体工质可以采用水或CO2。考虑到CO2具有更高热膨胀系数和更小的黏度，有助于热储中自然对流的形成[10]，并且与CO2地质封存相结合提供系统的综合收益，在本次研究中采用了CO2作为热储中的工质。在开采过程中，流体工质的温度变化通常在100℃以上，工质密度、黏度和比热容等参数都会出现较大幅度的改变。因此在本次研究中采用了与Cao 等[19]相同的变物性模型，将流体工质的密度、黏度、热导率和比热容视为工质温度和压力的函数，并在数值计算时于每一个迭代之前进行修正。

计算基于Fluent 软件进行，并利用了UDF 功能实现了上述数学模型。计算模型采用二维轴对称模型，以井筒中心轴作为对称轴。计算网格共计15498 个，经网格和时间步独立性测试，系统采热量计算的数值差分误差小于1%。

2 单井采热方案性能比较

基于以上模型，本文模拟了重力热管与套管式地下换热器两种单井地热系统30年的运行过程，并对两种系统的采热量与发电量进行了比较。

地热系统的采热量Q 和发电量E，采用式（19）、式（20）进行计算：

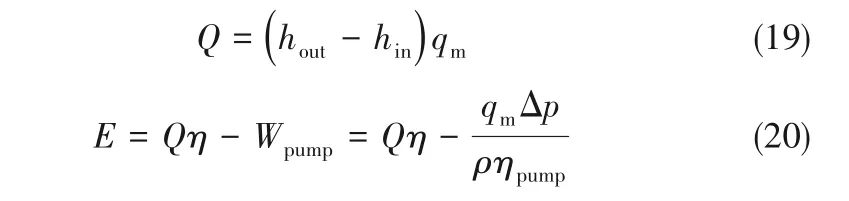
式中，hin为流入工质的比焓；hout为流出工质的比焓；qm为工质循环的质量流量；Wpump为套管式地下换热器的泵功消耗，对于重力热管地热系统该值为0；ηpump为 水 泵 效 率，取 为0.8[27]；η 为 热 电 转 化效率[8,27]：

式中，ηoi、ηm、ηg分别为汽轮机内效率、汽轮机机械效率和发电机效率，取值依次为0.8、0.97、0.98[8,27]；ηth为理想热效率，可由卡诺定理计算得到：

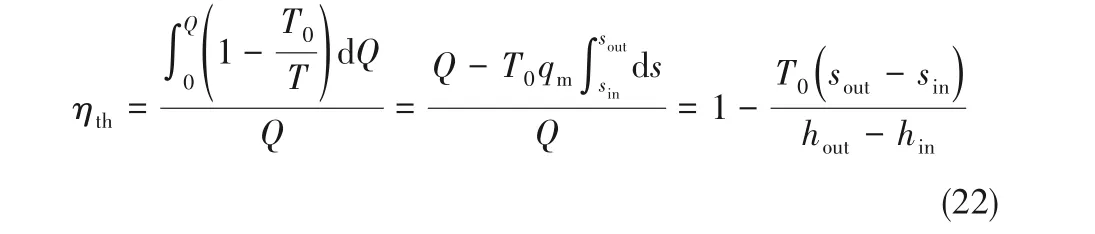
式中，T0为环境温度，按25℃计算；sin为流入工质的比熵；sout为流出工质的比熵。

2.1 采热性能与发电量

从图3（a）中可以看出，存在裂隙热储（渗透率为10-12m2）时，重力热管式采热系统的采热量（1560 kW）远高于套管式采热系统（850 kW）。然而，当不存在裂隙热储（渗透率为0）时，套管式采热系统的采热量（650 kW）高于热管式采热系统（410 kW）。对于重力热管采热方案，裂隙热储产生的自然对流作用能够使该方案采热量提升280%以上；但对于套管式采热方案，裂隙热储只能使其采热量提升约30%。很明显，相对于套管式采热方案，重力热管式采热方案能够更加充分地利用热储中的自然对流作用。

图3 重力热管式和套管式地热系统采热量（a）与发电量（b）比较Fig.3 Comparison of heat extraction rate(a)and electric power production(b)between heat pipe and DHE geothermal system

通过式(20)、式(22)，可根据两种单井地热系统采热过程的模拟结果计算出系统的净发电量，结果如图3（b）所示。当存在裂隙热储时，重力热管地热系统的采热量（1560 kW）是套管式地热系统采热量（850 kW）的1.8倍，而前者的发电量（240 kW）则是后者（100 kW）的2.4 倍。可以看出，重力热管地热系统的热电转化效率明显更高。这是因为重力热管地热系统产出为气态工质，可以通过冷凝进行恒温放热；而套管式地热系统产出为液态工质，其放热过程会伴随工质温度的下降，从而降低了其热电转化效率。根据式(22)可计算得到100℃的水蒸气与164℃的液态水所能够获得的卡诺效率大致相等。因此重力热管传热系统能够在更低的采热温度下，维持较高的热电转化效率，从而大幅提升了地热电站的产出能力。

2.2 热储中的自然对流效应

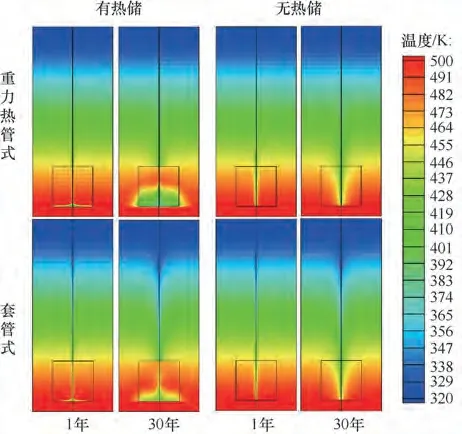
图4 有、无热储时重力热管与套管式地热系统的温度场变化情况（轴向与径向坐标显示比例为1∶10）Fig.4 Temperature field variation in the heat pipe and DHE geothermal systems with or without a fractured reservoir(axial to radial=1∶10 for better view)

为了对热储中的自然对流效果进行评估，分别显示有、无热储的重力热管系统与套管式地下换热器系统在1 年和30 年开采时间下的温度场（图4）。可以看出，对于无热储算例，其温度场为典型热传导式温度场，热管壁面对热储度的影响随着时间缓慢地在热储中扩散开来。当存在裂隙热储时，从其1～30 年的温度场的变化过程中可以看出，随着采热过程的进行，被井筒冷却后的流体流向热储底部，并在底部区域逐渐积累。

在管体附近选取了热储的顶部、中部和底部（深度分别为3550、4000 和4450 m）的三个区域，对其渗流场进行了局部放大，如图5所示。可以看出，在管体附近的槽道中存在较强的垂直向下流动，这是由于槽道中的流体被管体冷却之后密度增大，并在重力的作用下向下流动。同时，当热储底部的槽道中聚集大量密度较大的冷工质时，槽道内部的压力会高于周围热储，因此冷工质会不断地从槽道底部流向热储中。并且，该过程会在管体上部区域产生虹吸效应，使热储中的热流体不断补充到上部的槽道中，从而增大了管体周围环境的平均温度，提升了系统采热量。

从图4 可以看出，热管式地热系统开采30 年后在热储底部所积累的冷流体要明显多于套管式地热系统，说明热管式地热系统在裂隙热储中的自然对流强度明显高于套管式地热系统。进一步，从图5 中可以看出，重力热管式采热系统槽道中的最大流速要明显高于套管式采热系统，这说明重力热管式采热系统的槽道能通过热虹吸效应从热储中吸入更多的热工质，从而获得更高的采热量。

图6 显示了在有热储的情况下，套管式和重力热管式地热系统的管壁热通量与管内温度分布情况。从图6（a）中可以看出，在中浅层区域，套管式换热器管外的热通量要高于重力热管式换热器；但在3500 m 以下的热储区域内，重力热管式换热器管外的热通量大幅高于套管式换热器。图6（b）显示了两种采热方式管壁温度的分布情况。套管式井下换热器管内为单相流动，冷流体在外管与内管的环空中向下流动，并通过外管壁面从岩石中吸收热量，当工质吸收热量时其温度也会随之上升。而在热储区域，自然对流作用使得壁面热通量明显上升，也同时导致套管内部工质温度迅速上升，导致管壁与岩石温差减小，从而降低了热储中的自然对流作用。但对于重力热管采热系统，管内工质通过相变将热量储存在气体工质的潜热中，不会导致管内温度的上升。从图6（b）中可以看到，在3500 m 以下的热储区域，热管壁面的平均温度大致为110℃，比套管式井下换热器的管壁温度低40℃左右。很明显，重力热管采热系统能在热储区域内获得更大的传热温差，从而可以更好地利用热储中的自然对流作用来强化系统的采热性能。

图5 采热进行30年时有热储的重力热管式地热系统热储内部的渗流场Fig.5 Seepage flow in the reservoir of heat pipe geothermal system at 30 a into the process

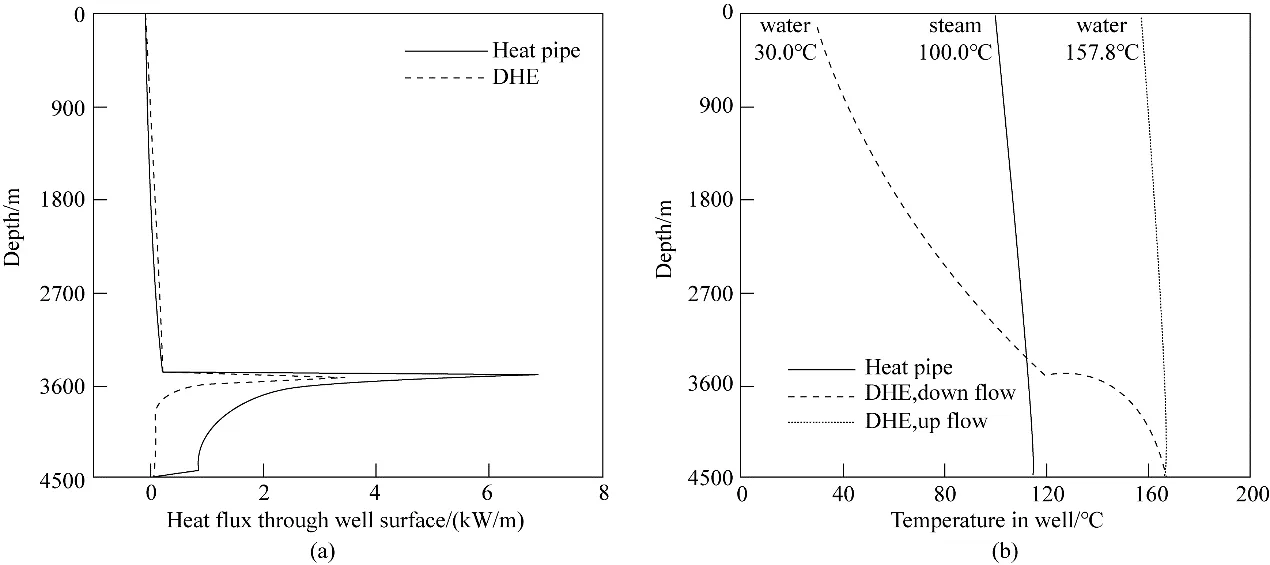
图6 采热进行30年时有热储的重力热管式和套管式地热系统壁面的热通量（a）和温度（b）分布情况Fig.6 Heat flux through well surface(a)and temperature in well(b)along the well-depth direction for the heat pipe and DHE geothermal systems with a reservoir at 30 a into the process

热储中自然对流的产生对裂隙热储的渗透率具有一定的要求。在以上算例中热储渗透率设定为10-12m2，为了显示渗透率对热储自然对流强度的影响，本文进一步模拟了渗透率为10-11、10-13、10-14m2时系统的运行情况。从图7 中可以看到，渗透率大于10-13m2时，对比无热储算例，裂隙热储中的自然对流作用能使重力热管地热系统采热性能提升190%以上；同时，当热储渗透率大于10-12m2时，进一步提升热储渗透率对系统采热性能的影响并不是十分明显，当渗透率为10-11m2时，其采热量仅比渗透率为10-12m2的算例高出4.5%。将以上现象结合图5 中的渗流分布情况可以推测出，当渗透率小于10-14m2时，槽道底部的冷工质向热储中的渗流速度较慢，因此冷工质会在槽道中大量聚集，从而降低管体周围环境的平均温度，进而降低系统采热量；而当渗透率大于10-12m2时，槽道底部的流体工质可以顺利地流入热储中，不会在槽道中产生明显聚集，因此进一步提升渗透率并不会对系统采热性能产生影响。在之前的研究工作中[10]，已对影响该系统热储中自然对流强度的其他因素（如热储半径、高度、渗流槽道、热管温度等）进行了较为详细的论述分析。

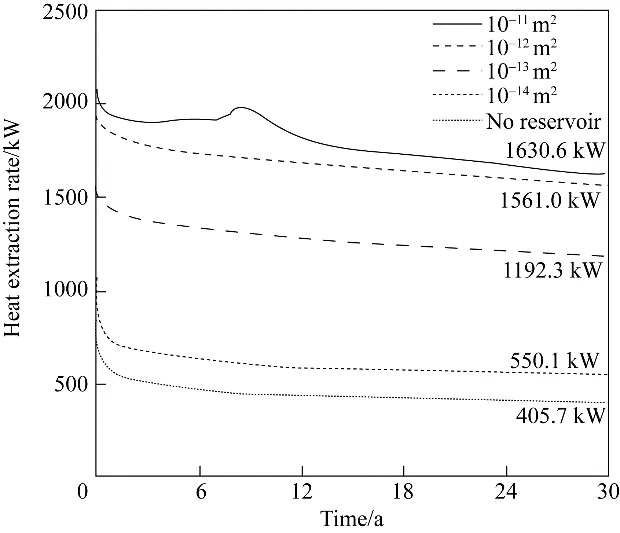
图7 热储渗透率对重力热管地热系统采热量的影响Fig.7 Influence of reservoir permeability on the heat extraction performance of gravity heat pipe system

3 发电经济性评估

基于前文中的模拟结果，本部分将对重力热管地热系统的全生命周期的平均发电成本进行计算，并与DHE 和EGS 地热电站进行比较。从前文中的模拟结果中可以看出：热储对套管式地热系统性能的提升幅度较小，而对重力热管式地热系统的提升幅度较大。考虑到热储的压裂会明显增加单井采热系统的建设成本，如果热储对系统采热量的提升幅度较小，建立人工热储反而会降低系统整体经济性。因此在评估两种单井采热系统的经济性时，分别选择了有热储的重力热管式采热方案和无热储的套管式采热方案进行评价。

综上，本次研究将对以下三种地热发电方案进行经济性评估：

（1）有热储的重力热管式采热方案，简称为“重力热管方案”；

（2）无热储的套管式采热方案，简称为“套管方案”；

（3）EGS方案。

3.1 成本电价模型及计算依据

现金流折现法是研究可再生能源电价成本时的常用方法[28-30]。这种方法参考了资本在该行业中的折现率，并将这一收益作为项目资金的使用成本，用于计算电站的运营期内的总成本。该成本电价计算公式为[30]：

式中，cLCOE为发电成本；CCAP为项目总投资；CO&M为系统年均运行维护费用；为系统生命周期内的平均发电量；γ 为资本折现率，本次研究采用火电站的常规折现率8%[31]；tyear为电站年运行时间，取360 d；n 为系统运行寿命，单井式地热系统采热温度不会随着采热过程出现明显下降，并且也没有常规地热系统存在的腐蚀结构问题，本次研究中认为单井地热系统的使用寿命为50年。

对于单井式地热系统，总投资主要包括四个部分：钻井总费用、井内改造费用、热储改造费用和电厂建设费用。

系统的运行维护费用主要为地热电站的运维费用。钻井总费用不仅与岩性及地质构造有关，并且还会随深度的增加而大幅上升。在本次研究中采用了与Huang 等[32]相同的方法来计算钻井费用：在0～1000 m 深度钻井费用计为1000 CNY/m，深度每增加1000 m 钻井费用增加1000 CNY/m。本次研究中井深为4500 m，据此计算得其钻井费用为1250万元。

井内改造费用主要为管体及管内结构成本：4500 m 管材总重约352 t，管材单价约为0.75 万元/吨，据此估算管体总价为264万元；热管内部结构费用大致估算为160 CNY/m，总计72 万元。本次研究中，套管方案仅考虑管体费用，计264 万元，而重力热管方案的管体与管内结构总费用约为336万元。

热储水力压裂的各项费用占比从高到低依次为支撑剂费用、水费、水泵功耗、化学激发剂费用及其他费用[33]。对于EGS热储，为了实现井下连通，压裂半径通常在500 m 左右，需要多次压裂，而单次水力压裂费用大致为250 万元[32]。对于本次研究中的单井采热系统，其热储直径仅为50 m，所需的压裂面积仅为前者的1/100，压裂过程中消耗的支撑剂、水及泵功远小于EGS 热储压裂过程中的消耗量。考虑到相关热储工程技术还在研发中、实际数据缺乏，故本次研究中将热储体积压裂所需总费用估计为500万元。

地热电站建设成本大致在14000 ～35000 CNY/kW（2000～5000 USD/kW, 2019）[29]，而地热电站的年均 运 行 维 护 成 本 为555～1733 CNY/kW（73～228 EURO/kW,2018）[34]，本次研究中的地热电站建设成本及维护成本取以上成本的中位数，分别为24500 CNY/kW和1144 CNY/kW。

3.2 发电经济性比较

对于重力热管及套管式两种单井地热电站，根据3.1 节中测算标准来估算其投资及运维费用，其发电量则参考2.1 节中的模拟结果；对于EGS 方案，其投资费用及电能产出参考了Cui 等[8]和Lu[35]对法国苏尔士EGS 电站投资成本及发电量的估算结果。基于以上数据，对三种地热电站的经济性进行了计算比较，其结果见表1。

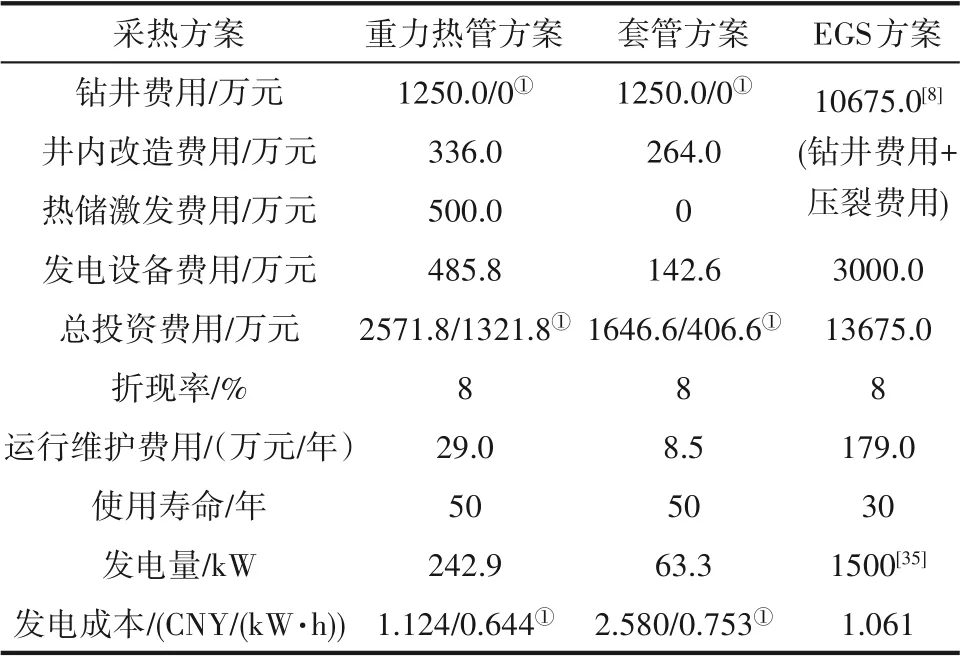
表1 三种采热系统发电经济性测算结果Table 1 Economic evaluation of the three geothermal power stations

从表1 中可以看出，EGS 方案的投资成本（13675.0 万元）远远高于其他两种方案。而套管方案的投资成本最低，仅为1646.6 万元。考虑到单井采热方案无须进行复杂的井下连通工程，可以更加充分地利用现有的废弃油气井。因此对于两种单井式开采方案，本文进一步给出了不包含钻井成本的评估结果。可以看出，当利用废弃油气井建设时，套管方案的投资成本仅为406.6万元。

表1中还给出了三种采热方案发电成本的计算结果。对于EGS 方案，其发电成本为1.061 CNY/(kW·h)，在三种采热方案中成本最低；重力热管方案发电成本（1.124 CNY/（kW·h））与EGS 方案非常接近；而套管方案发电成本（2.580 CNY/（kW·h））最高，是其他方案发电成本的2 倍以上。当利用废弃的油气井来建设单井式采热系统时，两种单井采热方案总投资成本会大幅降低，尤其对于套管方案，其投资总额下降幅度高达75.3%。在这种情况下，重力热管方案、套管方案的发电成本分别下降到0.644 CNY/（kW·h）、0.753 CNY/（kW·h），有望在上网电价较高的地区实现商业化运行。值得注意的是，对于我国北方等存在大量供暖需求的地区，可以在供暖季利用发电之后的尾水或部分高温热水（蒸汽）进行供暖，如果考虑供暖所带来的额外收益，以上三种地热系统的发电成本会进一步降低。

3.3 重力热管方案电价成本敏感性分析

由于地区条件的不同，以及产业技术的发展，重力热管的各项成本及系统性能可能会出现一定幅度的变化。本文将影响重力热管地热系统电价成本的各项参数以-75%～75%的变化幅度进行改变，用于显示其电价成本对各项参数的敏感性。所考虑的参数包括：折现率、钻井费用、热储激发费用、井内改造费用、电站设备费用、运行维护费用、系统寿命及发电量。计算结果如图8所示。

图8 成本电价对各项参数的敏感性Fig.8 Parameter sensitivity analysis of electricity-production cost

从图8 中可以看出，在重力热管地热系统各项费用成本中，钻井费用对系统发电成本的影响最大。当钻井费用从-50%～50%变化时，对应的发电成本为0.884～1.364 CNY/（kW·h）。而热储改造费用、井内改造费用、电站设备费用和运行维护费用对系统发电成本影响程度相对较小，当这些参数从-50%～50%变化时，发电成本的变化范围大致为1.030～1.220 CNY/（kW·h）。

当系统寿命从12.5年增长到25年时，系统的发电成本从1.701 CNY/（kW·h）降低到1.269 CNY/（kW·h）。但系统寿命进一步从25 年增长到50 年时，系统的发电成本仅从1.269 CNY/（kW·h）下降到1.124 CNY/（kW·h），并且进一步增加系统寿命几乎不会对其经济性产生影响。

地热系统的发电量的变化对其经济性的影响最为明显，当发电量从-50%～50%变化时，对应发电成 本 的 变 化 为2.249～0.75 CNY/（kW·h）。Huang等[10]的研究显示对于重力热管地热系统，当热管管壁与热储之间的温差增大100%时，由于热储中自然对流作用的增强，热管采热量的提升幅度约200%。本次研究中热管管壁平均温度大约为110℃[图6(b)]，热储平均温度为210℃，温差约为100℃；如果地温梯度增加到0.055℃/m，热储温度会上升到250℃，此时温差约为140℃，提升幅度为40%。参考文献中的研究结果[10]，此时系统采热量及发电量的提升幅度约为70%。结合图8 中成本电价随系统发电量的变化情况可大致估计，当地温梯度为0.055℃/m时，系统发电成本低于0.7 CNY/（kW·h）。

4 结 论

本文针对干热岩重力热管地热系统开发了全新的数值模型，能够对重力热管内部相变-流动过程与干热岩热储中渗流过程进行耦合求解。基于该模型，本文模拟了管长为4500 m 的重力热管地热系统与套管式地下换热器系统的运行过程，并研究了裂隙热储中的自然对流现象对这两种单井式地热系统性能的影响。进一步，本文参考了目前实际工程中的施工成本，对重力热管地热电站的成本回收电价进行了估算，并与EGS 和套管式地热系统进行了比较。得到以下结论。

（1）在重力热管底部设置裂隙热储能够明显提高系统采热性能。当热储渗透率大于10-13m2时，裂隙热储中的自然对流作用能使重力热管地热系统采热性能提升193.9%。

（2）对于单井式采热系统，重力热管采热方案能够更加有效地利用热储中的自然对流作用来提高系统采热量，并且能够获得更高的热电转化效率。当井底存在裂隙热储时，重力热管地热系统的采热量是套管式地热系统的1.8 倍，其发电量则是后者的2.4倍。

（3）重力热管地热系统发电量可达242.9 kW，成本电价约为1.124 CNY/（kW·h），与EGS 电站发电成本接近，但其投资总额仅为EGS 电站的约1/6，并且技术不确定性小，项目投资风险较低。

（4）当利用废弃油气井建设重力热管地热系统时，其成本电价仅为0.644 CNY/（kW·h）。并且与套管方案相比，重力热管方案的发电量约是套管方案的4 倍，能够更加充分地利用废弃油气井区的地热资源，具有规模化应用的潜力。

（5）钻井费用与地温条件对重力热管地热系统的经济性有很大影响。而热储改造费用、井内改造费用、电站设备费用和运行维护费用对系统发电成本影响程度相对较小。据估计，当地温梯度大于0.055℃/m 时，系统发电成本将低于0.7 CNY/（kW·h）。