基于导热形状因子的泡沫金属导热特性分析

2021-04-09杨振姚元鹏吴慧英

化工学报 2021年3期

杨振，姚元鹏，吴慧英

（上海交通大学机械与动力工程学院，上海200240）

引言

具有优异传热性能的泡沫金属材料在热储存[1]、能源器件温控[2]等领域（如工业余热蓄存回收、电子芯片散热、锂电池热管理等）应用十分广泛。这主要得益于泡沫金属高热导率与高度扩展的换热表面。其中，等效热导率（ETC）作为衡量泡沫金属导热特性的关键热物理参数，其精确计算对应用泡沫金属材料的热系统设计、性能评估至关重要。

为预测泡沫金属ETC，研究人员通常基于实测泡沫金属孔隙率与金属骨架、填充介质热导率构建相应理论模型。Calmidi等[3]以十二面体表征泡沫金属结构，并将泡沫骨架韧带与结点分别以2D圆柱和方块近似，首次提出了计算泡沫金属ETC的2D结构模型。Bhattacharya 等[4]将泡沫骨架结点假设为球形，更好地刻画了实际泡沫金属结构。Boomsma等[5]采用Kelvin 十四面体表征实际泡沫结构并将泡沫骨架韧带、结点分别近似为三维圆柱、方块，提出了预测ETC 的3D 结构模型。Dai 等[6]进一步引入泡沫骨架韧带取向影响，对Boomsma 等[5]的模型进行了修正和改进，提高了ETC 计算精度，但该模型中韧带、结点间的几何关系与物理实际存在难以调和的矛盾。Yang 等[7]同样基于十四面体泡沫结构（将泡沫骨架结点近似为长方体）提出了预测ETC的3D结构模型，避免了上述韧带、结点间的几何矛盾。需要指出，上述泡沫金属ETC 理论预测模型均基于各向同性的泡沫结构假设，且多关注泡沫骨架结构及其韧带、结点构型的合理简化，但模型预测结果与大量实验数据存在显著偏差（甚至高于20%）。

另外，有研究指出实际泡沫金属的多孔结构在各向存在显著差异。Gong 等[8]将沿泡沫结构拉伸方向与其垂直方向的胞径比定义为各向异性率，发现泡沫金属各向异性率最高可达1.46。Perrot等[9]以泡沫孔胞最大尺寸与最小尺寸之比表征孔胞形变程度，并证实了基于该方法可以对孔胞几何参数进行准确预测。此外，Jang 等[10]和Manonukul 等[11]的研究结果均表明，实际泡沫金属孔隙结构不满足各向同性结构假设。实际上，受重力、黏度等因素影响，泡沫金属在制备过程中往往会在重力方向存在一定程度拉伸形变，即其多孔结构在各向存在固有差异[12]，进而会导致泡沫金属各向导热特性差异显著。Bodla 等[13]数值计算了沿泡沫金属三个主要方向的平均ETC，发现沿不同方向的ETC 计算结果间相对偏差可达15%。Kumar 等[14]定向拉伸了Kelvin 十四面体以模拟实际泡沫结构形变，结果表明定向拉伸泡沫孔胞将增大该向ETC。Zafari 等[15]和Iasiello等[16]基于计算机断层扫描技术数值重构了泡沫金属孔隙结构，进而通过直接数值分析发现：泡沫金属ETC 取决于计算所沿的方向。以上分析表明，现有建立在各向同性基础上的ETC 理论预测模型计算结果与实验数据间的显著偏差，可归因于已有模型未能纳入实际泡沫结构定向形变影响。

鉴于此，本文将通过理论分析引入一个可考虑泡沫结构定向形变影响的导热形状因子（m），并基于文献报道的大量ETC 实验数据对m 进行计算和分析。进而，通过导热直接数值模拟建立m 与泡沫金属孔胞定向形变参数（即沿泡沫金属宏观传热方向与其垂直方向的胞径比）间的关联，形成定向预测ETC 的新方法。最后通过实验数据对上述方法进行验证，并将该方法与已有基于各向同性泡沫结构假设的ETC 理论模型作对比，以凸显其用于预测实际泡沫金属ETC的优势。

1 泡沫金属导热形状因子

1.1 导热形状因子

首先，任取一个孔隙率为ε、体积为VCV的控制体[包括金属骨架（将其简化为矩形，体积为Vs）与其孔隙内填充介质部分]做分析（图1）。该控制体上下端面（面积为ACV，间距为LCV）存在恒定温差（T1-T2），故其宏观传热方向为竖直向下。为考虑实际泡沫金属多孔骨架迂曲变化效应，假设骨架相对控制体内宏观热流方向发生倾斜，倾斜角度为θ（θ 表征实际多孔泡沫结构沿控制体宏观传热方向的形变程度，其变化范围为0°～90°）。

如图1 所示，泡沫骨架长度Ls与横截面积As分别为

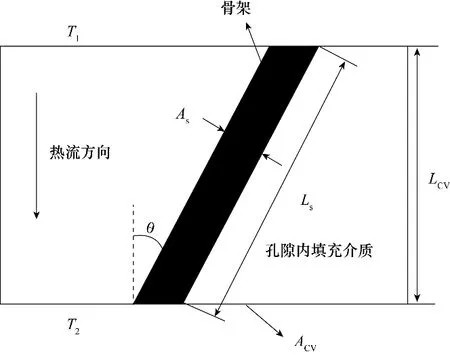
图1 泡沫金属控制体示意图Fig.1 Schematic diagram of the control volume of metal foam

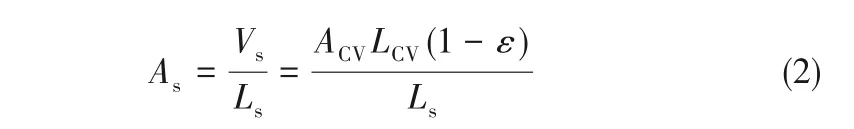
进而基于傅里叶导热定律，可推得金属骨架定向ETC（keff,s）[17]为：

式中，ks为金属骨架热导率。由于定温边界条件下泡沫骨架与填充介质间导热可忽略不计[18]，易得填充介质部分定向ETC（keff,f）为：

式中，kf为填充介质热导率。综合式（3）和式（4），最终可得整个控制体定向ETC为：

由式（5）可知，cos2θ 即为本文所提出的导热形状因子。令m=cos2θ，可得：

需要指出，理想泡沫金属（各向均匀同性，且各元胞几何结构完全相似）θ 值保持恒定，即其导热形状因子为确定参数（记为m0）。考虑到实际泡沫结构在各向存在固有差异，下面将基于文献报道的大量ETC 实验数据，通过式（6）对相应m 进行计算、分析，以揭示其变化规律。

1.2 基于实验数据的导热形状因子分析

基于式（6），通过给定泡沫金属样品的keff、ε、kf和ks数据，即可求得文献报道的实验数据所对应m值。图2 所示为m 随泡沫金属内不同填充介质（包括空气、水以及石蜡）的变化。由图2 可见，仅改变填充介质，m变化可忽略。显然，由于泡沫金属本身结构不受填充介质影响，因此m 亦不会受其影响，同时也验证了m作为导热形状因子的合理性。

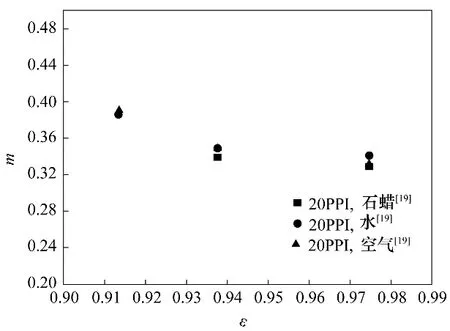
图2 不同填充介质时m的变化Fig.2 Variations of m with the filling media

图3 不同孔隙率、孔密度时m的变化Fig.3 Variations of m with the porosity and pore density

图3 给出了m 随泡沫金属孔隙率和孔密度的变化。由图可见，孔隙率或孔密度的变化均会对m 产生明显影响；且m 随孔隙率、孔密度的变化呈现出显著的随机波动现象，并无固定趋势或规律可循。事实上，泡沫金属结构难以由基于统计平均的孔隙率和孔密度参数完全确定，因此其m 值即使在相同孔隙率和孔密度时亦会存在不确定性波动。此外，不同实验中样品测定方向未统一，亦会造成m 计算结果的不同程度变化。需要指出，已有研究大都认为泡沫金属导热特性受孔隙率影响显著而受孔密度影响较小，但基于m 的分析则证实，孔密度对导热亦有不可忽略的影响，值得学界予以重视。

图4 进一步汇总了基于大量ETC 实验数据（涵盖不同材质、孔隙率与孔密度的泡沫金属样品）计算所得m 值。由图可见，不同实验数据对应的m 随机波动现象十分突出。故结合前述分析可知，对于任意泡沫金属样品，仅知其材质与孔隙率、孔密度参数，仍无法准确预测其ETC，须进一步纳入实际泡沫结构定向形变影响。为此，本文提出了基于导热形状因子定向预测泡沫金属ETC的新方法。

图4 基于大量实验数据[3,13,21-28]计算所得m波动变化Fig.4 Fluctuations of m calculated on a basis of a large amount of experimental data[3,13,21-28]

2 泡沫金属ETC定向预测

鉴于泡沫金属定向形变效应对其导热的重要影响，本部分首先引入表征实际泡沫结构形变的定向形变参数Ψ（定义为沿泡沫金属宏观传热方向与其垂直方向的胞径比）。进而，通过导热直接数值模拟建立m 与Ψ 间的关联，形成基于导热形状因子的定向ETC 预测新方法。最后，将该方法应用于实际泡沫金属样品ETC 预测，并与文献报道ETC 预测模型做比对，以验证本文方法的可靠性。

2.1 泡沫金属代表性单元体数值重构

首先采用图5所示体心立方结构及其定向形变结构进行泡沫金属代表性单元体数值重构[29]（ε=0.956，其各向孔胞直径分别为a、b、c，Ψ=b/a）。其中，图5（a）所示为各向同性泡沫结构；图5（b）为对各向同性泡沫结构定向拉伸（这里考虑Y 方向的拉伸，即b＞a，a=c）后所得各向异性泡沫结构。

下面将基于上述代表性单元体对泡沫铝-空气稳态导热问题进行直接数值模拟，以建立导热形状因子与定向形变参数间的关联。

2.2 泡沫铝-空气稳态导热问题与直接数值模拟

泡沫铝-空气（铝热导率为202.4 W·m-1·K-1，空气热导率为0.0265 W·m-1·K-1）稳态导热问题如图6所示。其中，代表性单元体上下端面（面积为AREV，间距为LREV）存在恒定温差（T1-T2），端面间热流为Q（宏观导热沿Y轴负方向）；此外，其余四个外表面均为绝热表面，且泡沫铝骨架与空气交界处温度、热流保持连续。

根据以上条件，进一步假设泡沫铝和空气的物性不随温度变化，则该纯导热问题能量控制方程为：

图5 泡沫金属代表性单元体数值重构[29]Fig.5 The numerical reconstruction of representative elementary volume of metal foam[29]

其边界条件如下：

上述能量方程由ANSYS FLUENT17.0求解器基于有限体积法在给定边界条件下数值求解（采用非结构化网格对图6 所示代表性单元体进行网格划分，经网格无关性验证后确定网格数为2481360个），当能量残差小于10-7时可认为计算结果收敛。进而根据傅里叶导热定律计算泡沫金属定向ETC（keff）：

本文通过逐步改变参数Ψ 以模拟孔胞的定向形变，重复上述计算步骤并结合式（6）即可给出m随Ψ变化的关联式。

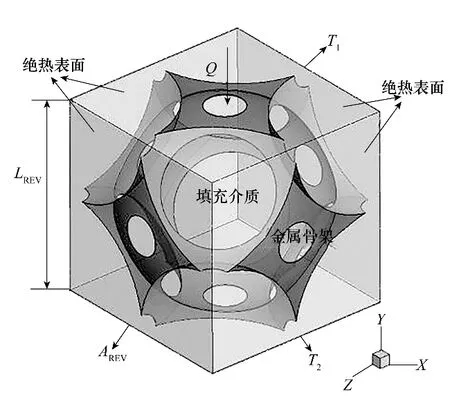
图6 泡沫铝-空气稳态导热问题Fig.6 A steady thermal conduction problem of aluminum-air

2.3 导热形状因子无量纲准则关联式

数值计算所得无量纲导热形状因子m/m0（对于各向同性泡沫结构，m0约为0.35[4,22]）随形变参数Ψ的变化由图7 给出。由图可见，m/m0随Ψ 增大而递增，即表明泡沫金属ETC 随孔胞拉伸方向形变程度增大而增大。这是因为定向拉伸泡沫孔胞会减小金属骨架在该向的迂曲度，也即减小了该向的导热热阻，最终表现为m 增大。进一步，为便于考量泡沫结构定向形变效应对泡沫金属导热特性的影响，本文以最小二乘法拟合建立了导热形状因子与定向形变参数间的无量纲准则关联式：

基于式（12），即可进一步由式（6）对实际泡沫金属ETC进行理论预测。

2.4 基于导热形状因子的ETC预测

为验证本文所提ETC 预测方法的可靠性，本节将基于前述导热形状因子对图8 所示姚元鹏等[30]实验中采用的泡沫铜-空气多孔介质样品（ε=0.942）ETC 进行预测。首先在图8 所示泡沫铜样品截面图近似均布地选取16个泡沫孔胞，测量样品沿宏观传热方向与其垂直方向的泡沫孔胞直径，并计算形变参数Ψ。进而，由式（12）、式（6）分别确定其导热形状因子和等效热导率。

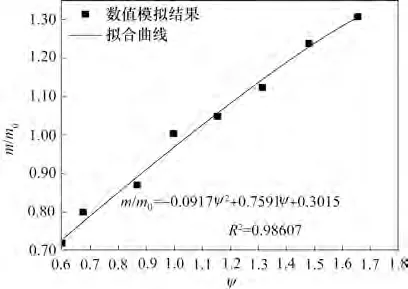
图7 m/m0随定向形变参数的变化Fig.7 Variation of m/m0 with the directional deformation parameter

本文方法计算所得ETC、姚元鹏等[30]报道实验结果及已有理论预测模型[3-5]所计算ETC 结果均汇总于表1。由表1可见，Calmidi等[3]模型、Bhattacharya等[4]模型、Boomsma 等[5]模型与实验结果[30]间相对偏差分别为14.27%、16.55%和42%，显著高于本文基于m 的ETC 计算结果与实验结果[30]间平均相对偏差（仅为0.77%）。可见，相比基于各向同性结构假设的理论预测模型，本文通过考虑实际泡沫金属孔胞形变效应影响，显著提高了ETC预测精度。

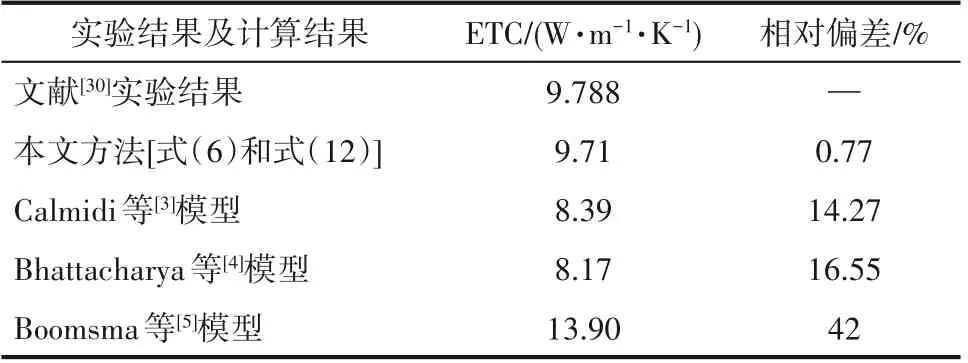
表1 不同ETC预测方法计算结果与实验结果偏差汇总Table 1 Relative deviations between experimental data of ETC and ETC results predicted by different methods

3 结论

图8 文献[30]实验所用泡沫铜样品截面图（ε=0.942，以空气为填充介质）Fig.8 Sectional view of copper foam sample employed in the experiment of Ref.[30](ε=0.942,with air as filling medium)

（1）m随泡沫金属材质、孔隙率及孔密度的变化呈现出显著的随机波动现象，无固定趋势或规律可循。需注意，与现有研究认为泡沫金属ETC 受孔密度影响较小的结论不同，基于m 的分析结果表明，孔密度对泡沫金属导热亦有重要影响。

（2）实际泡沫结构形变效应对泡沫金属导热影响显著，故对于实际样品，仅由金属材质、孔隙率和孔密度参数无法准确预测其ETC，还需考虑多孔结构定向形变影响。

（3）本文基于导热形状因子定向预测泡沫金属ETC 的方法（平均相对偏差0.77%）相比已有基于各向同性结构假设的ETC 理论预测模型（计算偏差＞14%）能显著提高ETC预测精度。

符号说明

A——面积，m2

a——X方向孔胞直径，m

b——Y方向孔胞直径，m

c——Z方向孔胞直径，m

k——热导率，W·m-1·K-1

L——长度，m

m——导热形状因子

Q——热流量，W