分层超立方网络的可靠性评估

刘西蒙，张郁芳，周书明，李小燕

（1.福州大学数学与计算机科学学院，福建 福州 350108；2.福州大学网络安全福建省高校重点实验室，福建 福州 350108；3.福建师范大学数学与信息学院，福建 福州 350007）

1 引言

随着多处理器系统规模不断扩大，处理器发生故障的情形不可避免。为了确保系统的稳定运行，需要对处理器进行测试和诊断，从而修复或更换有故障的处理器，以提高系统的可靠性。

故障诊断是评估系统可靠性和可用性的关键研究。系统中识别故障处理器的过程称为系统级诊断[1]。最早的系统级诊断模型由Preparata、Metze和Chien[1]提出，称为PMC 模型。PMC 模型通过相邻2 个处理器互相测试来进行诊断。Maeng 和Malek[2]提出了基于比较的MM 模型，该模型是通过一个处理器把任务发送到与它相邻的2 个处理器，然后比较它们的测试结果来进行诊断。随后，Sengupta 等[3]提出了MM*模型，该模型是MM 模型的一种特殊情况，在该模型下，每个处理器均对与它有直接物理相连的任意2 个不同处理器的测试结果进行比较。在系统级诊断中，如果系统可以检测出不超过t个故障处理器，则称该系统为t-可诊断的。在t-诊断系统中可以实现的t的最大值称为诊断度[1]。由于系统的最小度的限制，传统的诊断度很小。为进一步提高系统的诊断能力，Zhang 等[4]提出了一种新的度量方法，称为h-额外条件诊断度，并研究了超立方网络的h-额外条件诊断度。图G的h-额外条件诊断度（用(G)表示）是指在满足G中每个无故障分支至少包含h+1个顶点的条件下，G可以保证识别的最大故障顶点数目。Lin 等[5]研究了一些正则网络在PMC 模型下的h-额外条件诊断度（h=1 或2）。Huang 等[6]分析了交错群图在PMC 模型下的h-额外条件诊断度。Liu 等[7]研究了分层立方网络在PMC 模型和MM*模型下的h-额外条件诊断度。LYU 等[8]确定了一般正则网络在PMC模型和MM*模型下的h-额外条件诊断度（h=1或2）。Sun 等[9]研究了完全立方网络在PMC 模型和MM*模型下的h-额外条件诊断度。

t/s-诊断策略（即系统最多可以识别出t个故障顶点，其中至多s个无故障顶点被误诊为故障顶点）是一种十分高效的系统级诊断策略。Somani 等[10]基于t/s-诊断策略提出了t/s-诊断度，并研究了超立方网络和星形网络在PMC 模型下的t/s-诊断度；Fan 等[11]研究了双射连接网络的t/s-诊断度；Yang等[12]提出了立方网络的(4m-h)/3-诊断算法；Zhou等[13]给出了星形网络的t/s-诊断度；Lin 等[14]讨论了符合某些条件的正则网络的t/s-诊断度，并提出了一种t/s-诊断算法；Liang 等[15]研究了关于超立方网络在PMC 和MM*模型下的t/s-诊断度和t/s-诊断算法。此外，Xie 等[16]提出了关于超立方类网络的时间复杂度较低的t/s-诊断算法；Li 等[17]研究了数据中心网络DCell 在PMC 和MM*模型下的t/s-诊断度。然而，大多数网络在MM*模型下的t/s-诊断度和t/s-诊断算法尚未得到研究。

Malluhi 等[18]提出了一种新的互连拓扑，称为分层超立方网络，其拓扑结构适用于大规模并行系统，且通信效率较高。目前，关于分层超立方网络可靠性问题的研究较少，严重制约了分层超立方网络的应用和推广，基于此，本文对n维分层超立方（HHCn,n-dimension hierarchical hypercube）网络（后文简称HHCn）在PMC 模型和MM*模型下的h-额外条件诊断度和t/s-诊断度展开研究，设计了相应的t/s-诊断算法，并分析其时间复杂度。

2 准备工作

2.1 术语与符号

对于以下未定义的图论和网络术语，可以参考文献[19]。网络可以拓扑为图G=G(V,E)，其中每个顶点u∈V表示一个处理器，每条边(u,v)∈E表示处理器u和v之间的连接。在图G中，顶点v的邻集N G(v)表示在图G中与v相邻的任意顶点u的集合，即NG(v)={u∈V|(u,v)∈E}。类似地，子集S⊆V的邻集N G(S)表示与S中的某些顶点相邻但是不包含S本身的顶点的集合。由S导出的G的子图用G[S]表示，其顶点集为S，边集为{(u,v)|(u,v)∈E,u,v∈S}。根据邻域和子集邻集的定义可知，N G[S]=N G(S)∪S。当G在上下文中语义明确时，为方便起见，将省略下标G。顶点u在G中的度定义为d(u)=|N G(u)|。集合M和N的对称差集表示为

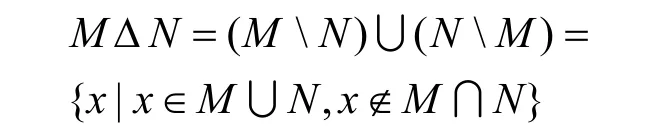
对于任意子集F⊂V(G)，符号G-F表示从图G中删除F中所有顶点，并删除至少有一个末端顶点在F中的边所得到的图。G-F的每个极大连通子图称为图G的一个连通分支，如果G-F是不连通的，则称F为点割集。G1≅G2表示G1与G2同构。mc(G) 表示图G的最大连通分支的顶点数目。表示{1,2,3,…,n}。图G的h-额外连通度是指使G-F不连通，并且剩余的每个连通分支的顶点数目不小于h+1的集合F的最小基数，用κh(G)表示。D表示PMC模型或MM*模型，(G,D)表示图G在PMC 模型或MM*模型下的h-额外条件诊断度。在本文中，“图”“网络”“系统”含义相同。

2.2 PMC 模型和MM＊模型

在PMC 模型中，对于系统G=G(V,E)中任意2 个相邻顶点u和v，当且仅当u测试v时，(u,v)∈E。G(V,E)中的测试结果集用函数σ:E→{0,1}表示，σ称为系统症候。用u测试v的结果表示为σ(u,v)。当u无故障时，如果v也无故障，则σ(u,v)=0；否则，σ(u,v)=1。如果u有故障，则σ(u,v)的值是不可靠的。

在MM*模型中，系统G=G(V,E)的比较方案可以刻画为一个多重图M(V,L)，其中V和L分别为G的顶点集和边集。若2 个顶点u和v都与顶点w相邻，则u与v可以通过w进行比较，即(u,v)w∈L。σ(u,v)w表示顶点w对2 个顶点u和v执行比较的结果。符号σ称为系统症候，定义为图G中所有比较结果的集合。当w无故障时，如果u和v都没有故障，则σ(u,v)w=0；否则，σ(u,v)w=1。如果w有故障，则σ(u,v)w的值可能为1 或0。在MM*模型中，如果(u,w),(v,w)∈E，则(u,v)w∈L。

引理1[20]对于系统G=(V,E)中的任意2 个不同故障子集F1和F2，当且仅当存在一个顶点u∈V-(F1∪F2)和一个顶点v∈F1ΔF2使(u,v)∈E时，F1和F2在PMC 模型下才是可区分的。

引理2[3]对于系统G=(V,E)中的任意2 个不同的故障子集F1和F2，当且仅当满足以下条件之一时，F1和F2在MM*模型下才是可区分的。

1) 有2 个顶点u,w∈V-(F1∪F2)，并且有一个顶点v∈F1ΔF2使(u,w)∈E和(v,w)∈E。

2) 有2 个顶点u,v∈F1-F2，并且有一个顶点w∈V-(F1∪F2)使(u,w)∈E和(v,w)∈E。

3) 有2 个顶点u,v∈F2-F1，并且有一个顶点w∈V-(F1∪F2)使(u,w)∈E和(v,w)∈E。

2.3 分层超立方网络

Malluhi 等[18]提出了分层超立方网络，它将n维带环立方网络[21]中的环用超立方网络替代。下面介绍分层超立方网络的定义和性质。

定义1[18]n维分层超立方网络HHCn用图来定义，其中顶点集为{(X,Y)|X=an-1an-2…a m,Y=am-1am-2…a0}，ai∈{0,1}，0≤i≤n-1，n=2m+m且m≥ 1。HHCn的顶点连接规则如下。

1) (A,Bl)对于所有0≤l≤m-1。

2) (Am+dec(B),B)，其中dec(B)是B的十进制值。

HHCn是由2n个顶点组成的(m+1)-正则二部图，每个顶点的度数为m+1，其中n=2m+m。HHCn由 22m簇组成，每个簇与m维超立方网络Qm同构。每个簇用Ci表示，i∈<22m＞。Q2m结构与HHCn结构如图1 所示（其中，m=2，n=6）。

图1 Q 22结构与HHC6结构

情况2X中的顶点至少分布在2 个不同的簇中，如图2 所示。

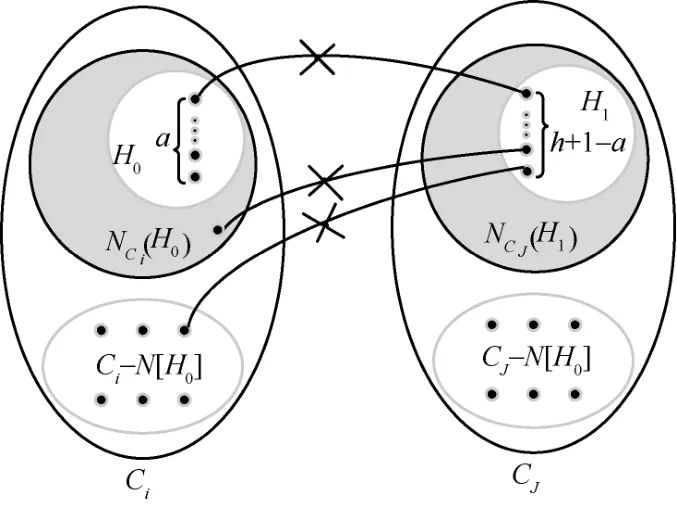
图2 引理7 情况2 示意

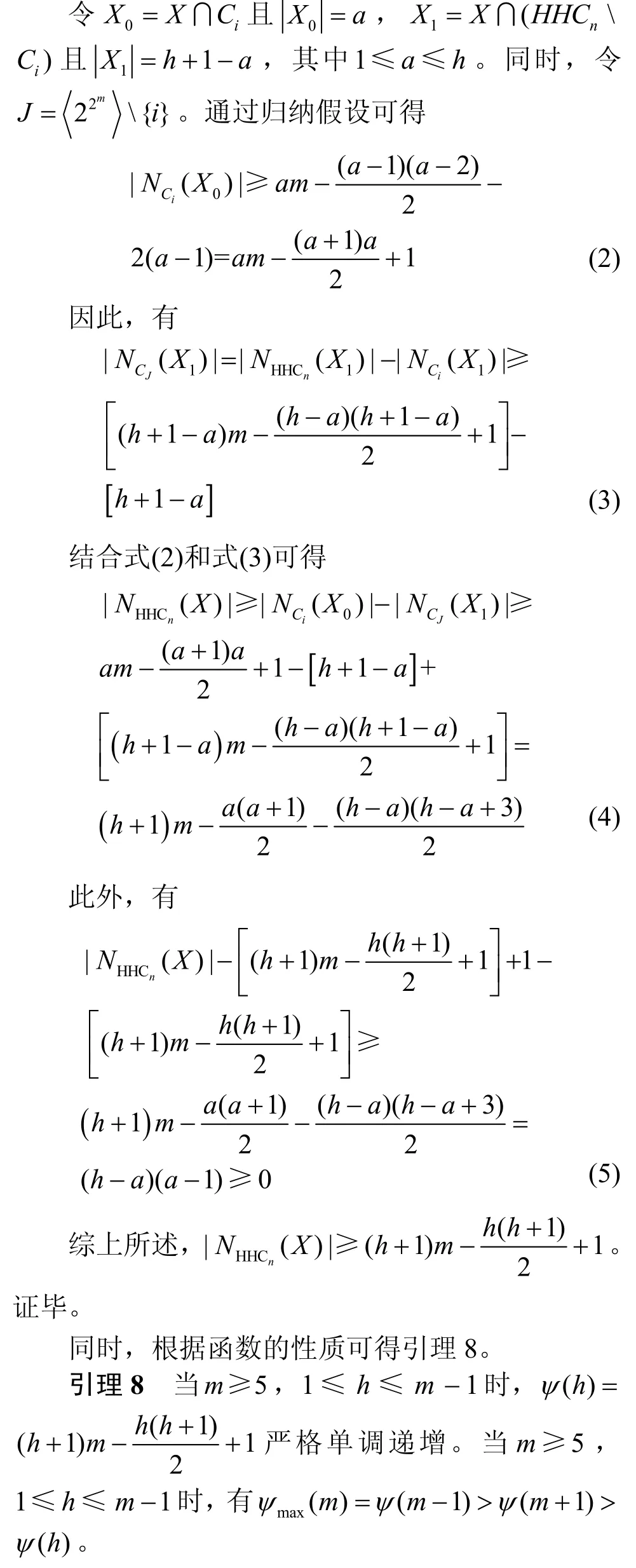
3 分层超立方网络的h-额外条件诊断度

本节将对分层超立方网络在2 个不同的模型下的h-额外条件诊断度进行研究。

定义2[4]在图G=G(V,E)中，当G-F是不连通的且G-F的每个分支至少含有h-1 个顶点时，称故障集F为h-额外故障集。

定义3[4]对于图G=G(V,E)中任意一对不同的h-额外故障子集F1,F2⊂V满足|F1|≤t和|F2|≤t，且F1,F2是可区分的，则称图G是h-额外条件t-可诊断的，使图G是h-额外条件t-可诊断的t的最大值，称为图G的h-额外条件诊断度，记作～t h(G)。

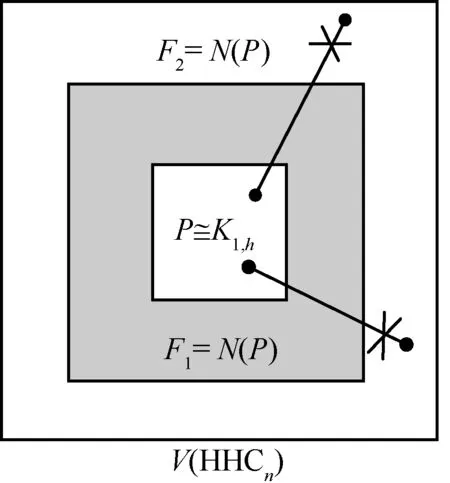
图3 引理10 示意

证明记P是HHCn中一个簇C1的一个顶点子集，其中HHCn[P]≅K1,h，F1=N(P)且F2=F1∪P。设S=N(P) ∩(HHCn-C1)，通过引理5 和HHCn的性质可得

因此，根据引理4 和引理9 可知引理11 成立。证毕。

根据引理10 和引理11，可以得出定理1。

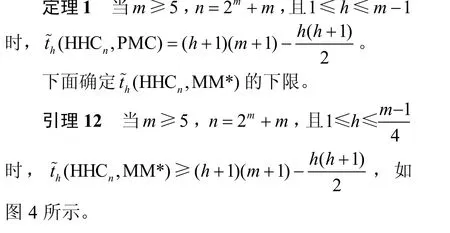
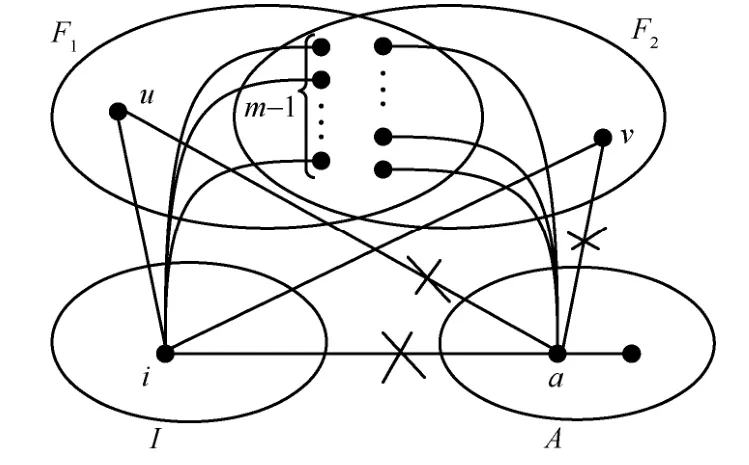
图4 引理12 示意

声明1J不包含孤立的顶点。

假设I(≠∅)是J中的一组孤立顶点集。显然，对于任意i∈I有I≤2n-1，N(i)⊆F1∪F2。此外，|F1F2|≥ 1，|F2F1|≥ 1。否则，如果F2F1=∅（或者F1F2=∅），则F1⊆F2。也就是说N(i)⊆F2，则i是HHCn-F2中的一个孤立顶点，这与h≥ 1的条件相矛盾。另一方面，如果在F1F2中存在2 个顶点u和v使(u,i),(v,i)∈E，则(F1,F2)是可区分的，这与假设相矛盾。如果不存在顶点u∈F1F2使(u,i)∈E，则HHCn-F2中的i是一个孤立顶点，这与h≥ 1的条件相矛盾。因此，N(i) ∩(F1F2)=1。同样地，N(i) ∩(F2F1)=1。因此，有

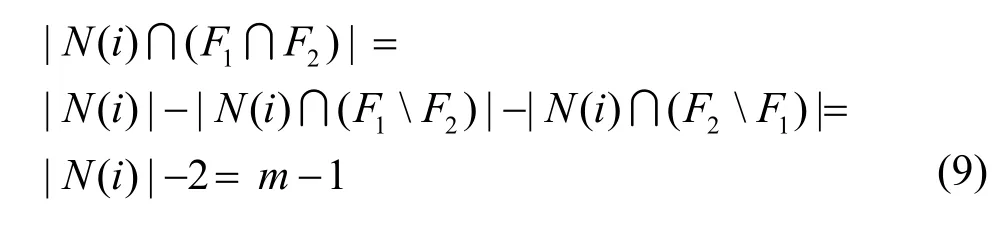
所以，|F1∩F2|≥ |N(i) ∩(F1∩F2)|=m-1。

令A=JI，接下来证明A≠∅。利用反证法，假设A=∅，可得

这是矛盾的，证毕。

根据引理10 和引理12，可以得出定理2。

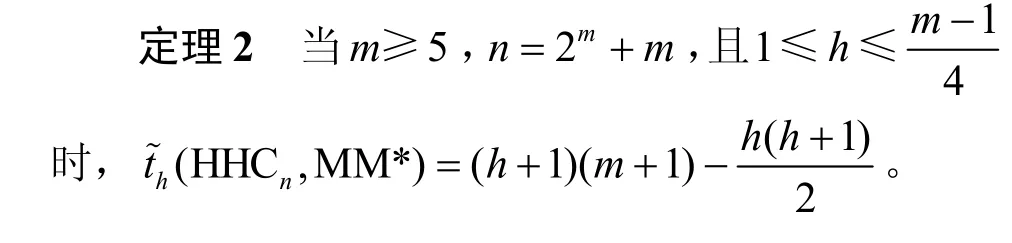
4 分层超立方网络的t/s-诊断度

本节将研究HHCn在PMC模型下以及MM* 模型下的t/s-诊断度（m≥5，n=2m+m，1≤s≤m-1）。此外，还将设计相应的t/s-诊断算法。

定义4[10]给定一个系统G，当系统中的故障顶点数目不超过t时，若对于任意症候σ，系统可以将所有故障顶点都分离在一个故障集合F′中，且F′包含至多s个无故障顶点，即F′≤|F|+s，则称这个系统是t/s-可诊断的。满足系统是t/s-可诊断的最大的t值称为t/s-诊断度。

定义5[12]给定系统G=(V,E)和在G中由故障集产生的症候σ。若T0(G)是G的0-测试子图，则需满足T0(G)是G的一个子图，同时V(T0(G))⊆V且E(T0(G))={(u,v)∈E,σ(u,v)=σ(v,u)=0}。

引理13[12]在PMC 模型下给定一个系统G=(V,E)以及在G中由故障集产生的症候σ，有如下结论。

1) 令u,v是G中的 2 个相邻顶点。如果σ(u,v)=σ(v,u)=0，则要么顶点u和v均无故障，要么顶点u和v均存在故障。

2) 令C为T0(G)的分支，则C中的所有顶点要么都是故障的，要么都是无故障的。

定义6[17]给定系统G=(V,E)及在G中由故障集产生的症候σ。令x⊆V，顶点x的0-比较子集表示为C0(x)={c∈V|∃a∈V,σ(x,a)c=0}。G的0-比较子图记为T′(G)，表示为G的一个子图，其中，V(T′(G))⊆V且E(T′(G))={(x,c)∈E|c∈C0(x),x∈C0(c)}，如图5 所示。

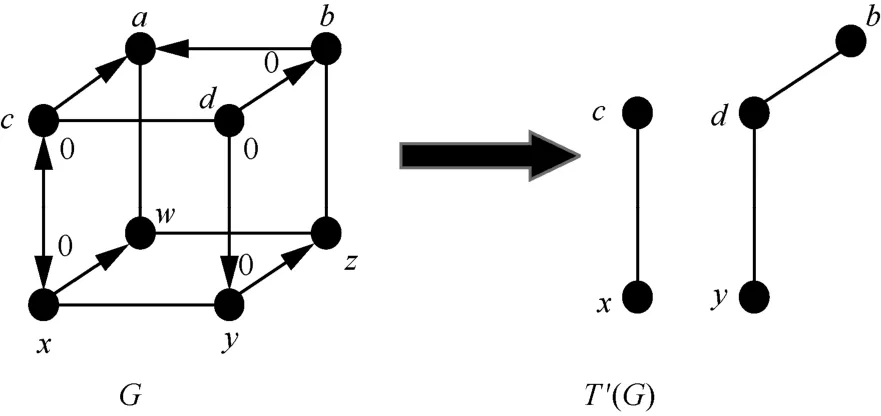
图5 G 的0-比较子图 T ′(G)的说明

引理14[17]给定一个至多包含t个故障顶点的系统G=(V,E)，以及在G中基于MM*模型由故障集产生的症候σ，有如下结论。

1) 如果对于任意2 个顶点x,y∈V且(x,y)∈E使y∈C0(x)和x∈C0(y)，则x和y具有相同的状态（即同为故障或无故障）。

2) 对于连通分支R⊆T′(G)，R中的所有顶点要么都是故障的，要么都是无故障的。

3) 如果T′(G)的连通分支R满足|V(R)|≥t+1，则R中的所有顶点都是无故障的。

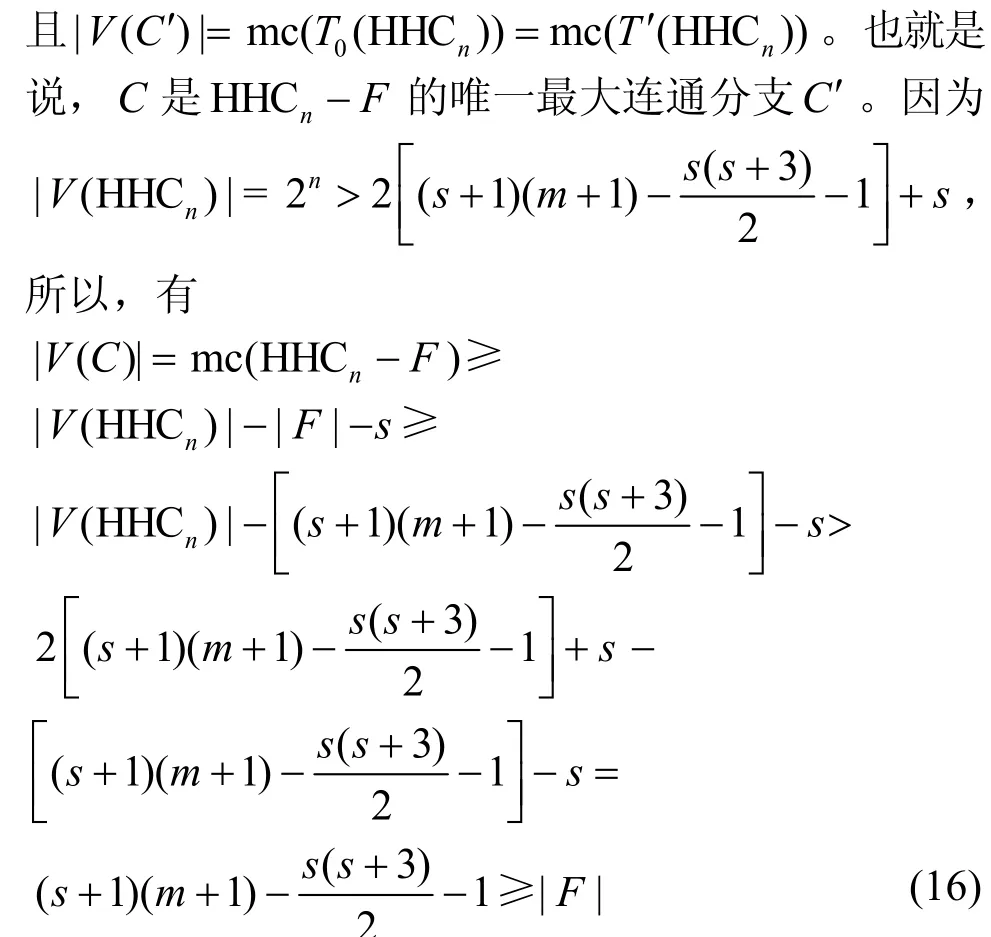
根据引理13中结论2)和引理14中结论2)可知，C中的所有顶点均为无故障，因此引理15 成立。证毕。

证明设F是HHCn的故障集，F′是所有故障顶点和可疑顶点的集合，C为T0(HHCn)或T′(HHCn)的最大连通分支。通过考虑F的大小进行证明。

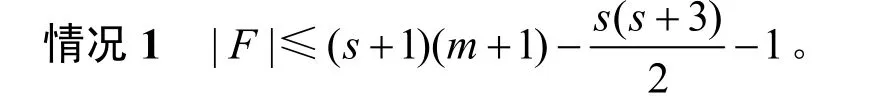
根据引理15 可得

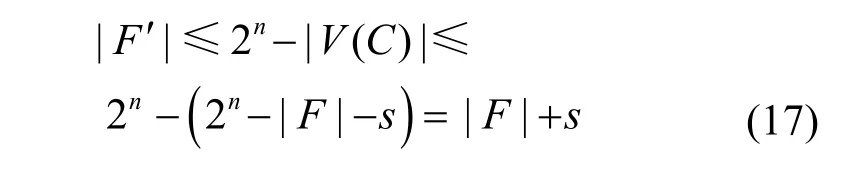
F′中最多包含s个无故障顶点。因此，在此情况下，定理3 成立。

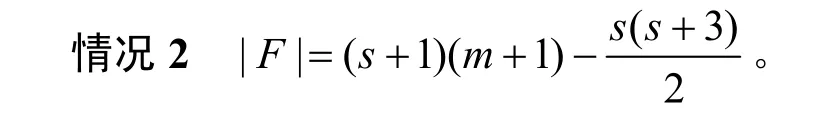
输出故障顶点集F′和无故障顶点集Y，其中F′∪Y=V(HHCn)

1) 初始化F′=∅，Y=∅，U=V(HHCn)，其中，∅表示空集。

2) 检查HHCn中所有的测试结果。↔表示2个顶点u和v在PMC 模型下相互测试。删除测试结果是1 ↔ 0、0 ↔ 1、1 ↔ 1的边，并将0 ↔ 0的边添加到E′中。令T0(HHCn)为E′的导出子图。

3) 获得无故障顶点的集合C。通过广度优先搜索在T0(HHCn)中获得最大连通分支C，并将C中的所有顶点添加到Y中。令U=U-Y。

4) 对于前面步骤中每个未诊断的顶点v，如果它的相邻顶点u∈C且σ(u,v)=1，则将v添加到F′中。令U=U-F′。

根据定理3 中情况2 可知，如果可疑顶点的数目超过s+1 个，则所有的可疑顶点都是无故障的。如果可疑顶点的数目少于s个，那么定理4 显然成立。

这意味着F′最多包含s个无故障顶点。因此，定理4 成立。证毕。

定理5当m≥ 5，n=2m+m，且1≤s≤m-1时，算法t/s-HHCn-DIAG-PMC 的时间复杂度为O(NlogN)，其中N=|V(HHCn)|。

证明算法t/s-HHCn-DIA G-PMC 主要时间成本在于获取T0(HHCn)的最大连通分支C，广度优先搜索算法最多运行O(N(m+1))次。因为log(2m+1)=m+1 ≤log(N)，所以获取T0(HHCn)的最大连通分支C的时间复杂度为O(NlogN)。其他每步的时间复杂度至多为O(N)。因此，算法t/s-HHCn-DIA G-PMC 的时间复杂度为O(NlogN)。证毕。

本文提出了一种在MM*模型下通过深度优先搜索（DFS,depth first search）定位HHCn的无故障连通分支的算法DFS-MM*，如算法2 所示。然后基于DFS-MM* 算法，提出了一个针对HHCn的t/s-诊断算法t/s-HHCn-DI AG-M M*，其中，T表示无故障的顶点集合，F′表示通过此算法被诊断为故障顶点的集合，H表示为未诊断(可疑)的顶点集合。

算法2DFS-MM*

输入HHCn中由故障集F产生的症候σ，顶点集R和顶点x∈HHCn

由定理3 中情况2 可知，若可疑顶点的数目超过s+1，则所有可疑顶点都是无故障的。相反，如果可疑顶点的数目小于s，那么定理6 显然成立。

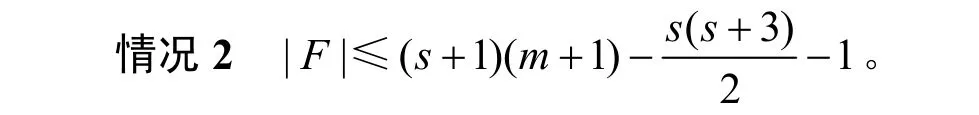
由引理3 可知，HHCn-F中存在一个唯一的最大连通分支K且V(K)≥V(HHCn) -|F|-s，那么HHCn中除去最大连通分支K外剩余的小连通分支至多包含s个顶点。根据t/s-HHCn-DIAG-MM*算法，当|V(K)|≥V(HHCn) -|F|-s＞t+1时，K中的所有顶点被诊断为无故障。在t/s-HHCn-DIAG-MM*算法中，如果|F′ |=t，则H中的所有顶点被诊断为无故障，没有顶点被误诊；如果|F′ |≠t，则将所有未诊断（可疑）顶点分离到F′中。因此，F′=V(HHCn)-T，其中T被诊断为无故障的顶点的集合。则有

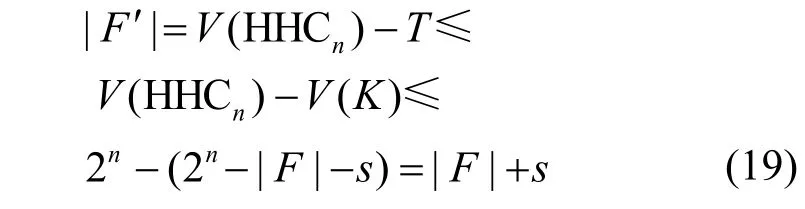
这意味着F′最多包含s个无故障顶点。因此，定理6 成立。证毕。

定理7当m≥ 5，n=2m+m，且1≤s≤m-1时，t/s-HHCn-DIAG-MM*算法的时间复杂度为O(NlogN)，其中N=|V(HHCn)|。

5 比较结果

在系统级诊断中，如果系统可以检测出不超过t个故障处理器，则称该系统为t-可诊断的。在t-诊断系统中可以实现的t的最大值称为诊断度，即传统诊断度[1]。根据t-可诊断的定义可知，分层超立方网络的传统诊断度为m+1 。本节对本文研究的分层超立方网络的h-额外条件诊断度、t/s-诊断度与传统诊断度进行比较分析，结果如图6 所示。

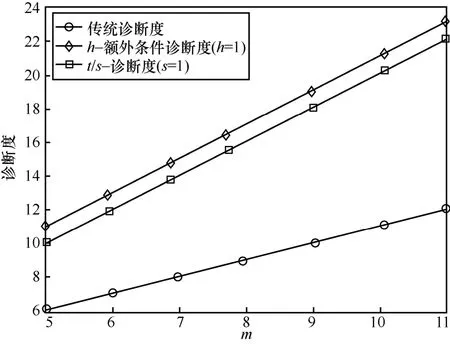
图6 HHCn 在3 种诊断策略下的故障诊断度（n=2m+m）

由图6 可知，当m≥5 时，分层超立方网络的h-额外条件诊断度、t/s-诊断度均大于传统诊断度，且分层超立方网络的h-额外条件诊断度是传统诊断度的h+1 倍，t/s-诊断度是传统诊断度约s+1 倍。因此，与传统诊断度相比，h-额外条件诊断度和t/s-诊断度提高了网络的诊断度，能更好地评估分层超立方网络的可靠性。

6 结束语

本文的研究成果有利于进一步评估分层超立方网络的可靠性，为分层超立方网络的应用和推广奠定了的理论基础。在接下来的工作中，可以考虑使用t/s-诊断算法监控分层超立方网络中的故障服务器。此外，郭晨等[26]研究了交换交叉网络在PMC模型下的(t,k)-诊断度，熊茜等[27]研究了交换超立方网络在PMC 模型下的(t,k)-诊断度，受其启发，分层超立方网络在PMC 模型和MM*模型下的(t,k)-故障诊断问题将是下一个研究内容。