基于无线供能反向散射通信系统安全性的稳健机会约束优化算法设计
2021-04-09郝万明谢金坤孙钢灿朱政宇周一青
郝万明,谢金坤,孙钢灿,朱政宇,周一青
(1.郑州大学河南先进技术研究院,河南 郑州 450003;2.郑州大学信息工程学院,河南 郑州 450001;3.郑州大学产业技术研究院,河南 郑州 450001;4.中国科学院大学计算技术研究所,北京 100049)
1 引言
随着物联网(IoT,Internet of things)技术的快速发展,无线传感器开始大规模部署。因传感器节点部署环境的随机性和复杂性,很难通过更换电池或接入电网为其供电。另外,频繁的信息交互与窃听者的存在也带来了能量短缺和信息安全问题。因此,如何解决节点能量短缺问题以及保证其数据安全是未来IoT 发展的关键[1]。
为解决无线传感器节点能量短缺问题,无线供能通信系统(WPCS,wireless powered communication system)和反向散射通信系统(BCS,backscatter communication system)被提出。WPCS 通过在终端用户嵌入能量收集模块,使终端用户可以通过无线的方式从专用能量站或环境中已存在的射频信号收集能量,提高了为其供电的灵活性[2]。然后,学者提出以下3 种可行的技术方案。1) 将WPCS 与IoT 技术相融合,通过部署专用的能量基站为传感器节点提供能量,传感器节点利用收集到的能量以传统的信息传输方式进行数据通信[3-4]。2) 将BCS与IoT 技术相融合,传感器节点通过反射调制的方式,将自身信息加载到外来射频信号上,实现低功耗数据传输[5],文献[6]的实验结果表明,BCS 中传感器节点的功耗大约为11 μW,远小于传统无线通信系统的功耗。3) 将WPCS 与BCS 相结合,形成无线供能反向散射通信(WPBC,wireless powered backscatter communication)系统[7-8]。由于传感器节点所处环境的复杂性,通过WPCS 收集到的能量是有限的,可能不足以激活能量基站覆盖范围的所有传感器节点进入工作状态[9]。相比于WPCS,采用BCS 的节点不需要产生射频信号和进行数模转换,因此可以进一步降低传感器节点工作的能量门限值,使其能够在一个较低能量值的情况下进入工作状态。对比以上3 种方案可得,WPBC 系统可以同时具有WPCS 和BCS 的优点,极大降低了系统功耗,更加适用于能量受限的传感器网络[10]。
传统的供电方式是通过明线、对称电缆及光纤等有线线路对设备进行直接供电。虽然有线供电可以保证系统的安全性和可靠性,但是复杂的布线和昂贵的铺设成本在一定程度上限制了其进一步发展。IoT 的传感器节点数量巨大,而且其分布环境也是复杂的、人为不可控的,导致有线供电极端困难。随着无线通信的快速发展,通过无线方式对IoT设备进行供电引起了工业界和学术界的广泛关注,WPCS 应运而生。
在能量传输过程中,无论采用的是传统有线供电方式还是新型无线供电方式,对于供电过程本身,一般不考虑电力在传输过程中的安全性问题,更关注电力在传输过程中的损耗问题。但是,无线供电与传统的有线供电在工作原理上存在本质区别。无线供电一般是以信号的无线传输为载体,通过信号本身携带的能量实现能量或信息传输。另外,信号在实现能量传递的过程中关注能量的转化效率,而在实现信息传递的过程中关注信息传输的安全性问题。所以,作为无线供电主要方式的WPCS与传统的有线供电方式相比,虽然在一定程度上解决了有线铺设的开销问题,但是由于无线供能同时伴随着信息的传输,为系统信息传输的安全性带来了隐患,因此在WPCS 中需要考虑其安全性。文献[11]对有线供电和WPCS 的优缺点进行了分析总结,将WPCS 作为有线供电的一种补充方式,以此来克服有线供电的缺点,并提出了一种基于双频双网体系结构的专用无线供电网络,来满足WPCS 对安全性和可靠性的需求。文献[12]在传统IoT 的基础上,提出了电力IoT 的概念,总结了电力IoT 的体系架构和技术支撑,并强调了WPCS 是实现电力IoT 的关键技术。
对于信息安全,传统方法是在网络层从密码学的角度进行考虑,通过设计各种加解密算法来提高系统的安全性,加解密算法越复杂,其安全性越高。由于IoT 中传感器节点体积、造价和计算能力等均有限,因此利用密码学实现信息安全并不现实。近年来,物理层安全(PLS,physical layer security)吸引了不少研究者的关注,它可以作为上层加密方法的一种补充或替代,通过物理层相关技术提高IoT中的安全性[13-16]。人工噪声(AN,artificial noise)是一种在物理层增强系统安全的有效手段,通过在发射端加入AN,以牺牲部分发射功率为代价,人为增大合法用户和窃听者之间的信道条件差距,保证在合法用户不受较大影响的同时对窃听者进行强干扰,从而实现安全传输[17]。另外,波束成形技术可以通过控制信号的传输方向增加目标接收机的接收信号强度来提高保密率。文献[18]研究了基于WPCS IoT 系统的安全传输问题,在传感器节点进行反射调制时引入AN,从而对窃听者进行人为干扰,来提高系统的安全性;并分别在理想信道状态信息(CSI,channel state information)和非理想CSI 情景下,考虑总功率约束、能量因果关系约束和功率分配系数约束,提出一种联合优化发射总功率、功率分配系数的方案,实现系统总保密率最大化。文献[19]考虑了一个全双工的WPCS IoT 系统,在总传输时间和波束成形系数的约束条件下,联合优化传输时隙和波束成形向量,实现系统总保密率最大化。
为了进一步提高WPCS 的能量效率和性能,越来越多的学者开始研究WPBC 系统中的安全问题。文献[9]研究了基于多用户资源分配的安全问题,考虑系统保密率和最小收集能量约束,提出一种联合优化反射时间、载波和人工噪声的方案,使系统安全速率最大化。文献[13]研究了单输入单输出(SISO,single input and single output)的WPBC 系统中的PLS 问题,通过弗里斯传输方程建立信号传输功率损耗模型,并讨论了该模型下获得保密率的条件。文献[14]考虑了一个多输入多输出(MIMO,multiple input multiple output)的WPBC 系统,在能耗受限的条件下最优化系统保密率,并提出一种有效的预编码方案。文献[20]研究了多用户MIMO 的WPBC系统,提出一种联合优化预编码矩阵、人工噪声协方差矩阵和功率分配系数的方案,实现系统安全速率最大化。但是在对WPBC 系统进行性能分析时,CSI 起着关键的作用。考虑到WPBC 系统中前向链路和反射链路之间的相关性以及系统对能耗的限制,传统的信道估计技术并不能直接应用于WPBC系统中。目前,大多文献假设通过信道估计技术可获得理想CSI[21-22],尽管这种假设可以使问题分析变得相对简单,但由于无线信道的随机特性,估计的CSI 往往会存在一定误差[23-24]。因此在对系统性能进行分析时,需要将信道估计误差考虑在内。
考虑到信道估计误差对整体系统性能的影响,文献[25]研究了多输入单输出(MISO,multiple input single output)的WPCS 的安全通信问题,并将其提出的算法拓展到非理想CSI 的通信场景,分别讨论了不加入AN 和加入AN、理想CSI 和非理想CSI的交叉场景。然而,文献[25]只考虑了WPCS 的能量收集方式,没有考虑结合反向散射通信来进一步降低系统的能耗。文献[26]研究了SISO 的WPBC系统稳健资源分配问题,并基于信道不确定性,研究了最大化多用户传输速率最小值的优化问题。文献[27]针对反向散射辅助的无线供能通信网络中由于信道质量差异导致的用户能效不公平问题,提出一种基于最大最小准则的资源分配方法,考虑用户服务质量与能量因果约束,并以最大最小化用户能效为目标,将优化问题建模为混合整数非凸分式规划问题,提出一种迭代算法来获取原优化问题的最优解,有效地保障用户能效的公平性。然而文献[26-27]均未考虑系统的安全问题。
综上所述,目前对考虑存在信道估计误差的WPBC 的稳健安全性问题还没有得到很好的研究。为提高通信系统安全性和可靠性,进一步降低系统能耗,本文做了如下研究。首先,建立WPCS 和BCS 结合的低功耗WPBC 安全通信系统模型。考虑存在信道估计误差条件下建立最大化用户数据传输速率最小值的优化问题,并满足最小收集能量约束、最大窃听速率约束、反射率约束和误差概率约束。由于所建立的问题含有不确定参数,直接获得解析解存在较大困难。考虑信道估计误差一般服从高斯分布,本文利用伯恩斯坦型不等式的安全逼近方法,将含参数摄动的约束条件和目标函数转换为确定性的形式。然后,结合不等式的性质,引入相应的辅助变量,将确定性优化问题转换为凸优化问题。最后,利用标准的凸优化算法进行求解,仿真结果表明了所提算法的有效性。
2 系统模型
如图1 所示,为方便讨论,考虑由单个全双工信号接入点(AP,access point)、单个用户和单个窃听者组成的WPBC 系统,其中AP 配置两根天线,用户和窃听者均配置单根天线。但所提算法不局限于典型的射频识别(RFID,radio frequency identification)系统,同样适用于传感器网络[13]。假设用户为无源设备,AP 采用WPCS 工作方式,同时为用户发送信息和无线充电。用户采用反射调制方式,将传输的数据经过调制后发送至AP,从而实现用户和AP 之间的数据传输。但是,窃听者可以通过无线信道窃听用户传输的数据,为系统带来安全隐患。本文采用准静态衰落信道模型,保证信道在一个数据传输阶段内不变,其中hrt、htr、hre、hte分别表示AP 和用户之间的通信链路、用户和AP之间的反射链路、AP 和窃听者之间的通信链路、用户和窃听者之间的窃听链路。
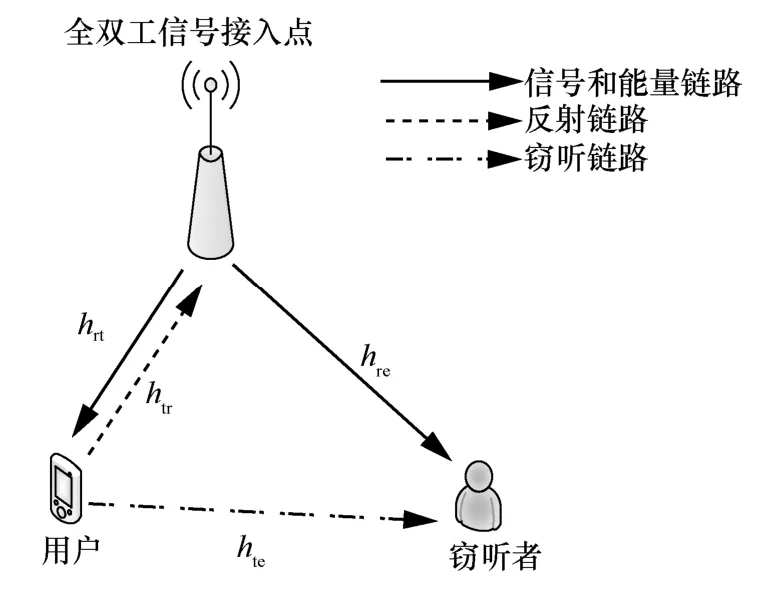
图1 系统模型
假设AP 配置的两根天线分别用于发送和接收信号,本文的主要参数及其含义如表1 所示。

表1 本文的主要参数及其含义
用户的内部结构如图2 所示,其由天线、能量收集单元、编码器、微控制器单元等组成。用户通过调节天线阻抗,可以在反射信号和接收信号这2 种工作状态间进行切换[26],从而使入射的射频信号为电路供电或传输自身信号。假设AP 的发射功率为p,用户的反射率为α,能量收集效率系数为η,由图2 可知,AP 的发射功率中(1 -α)p部分可以用于能量转换。
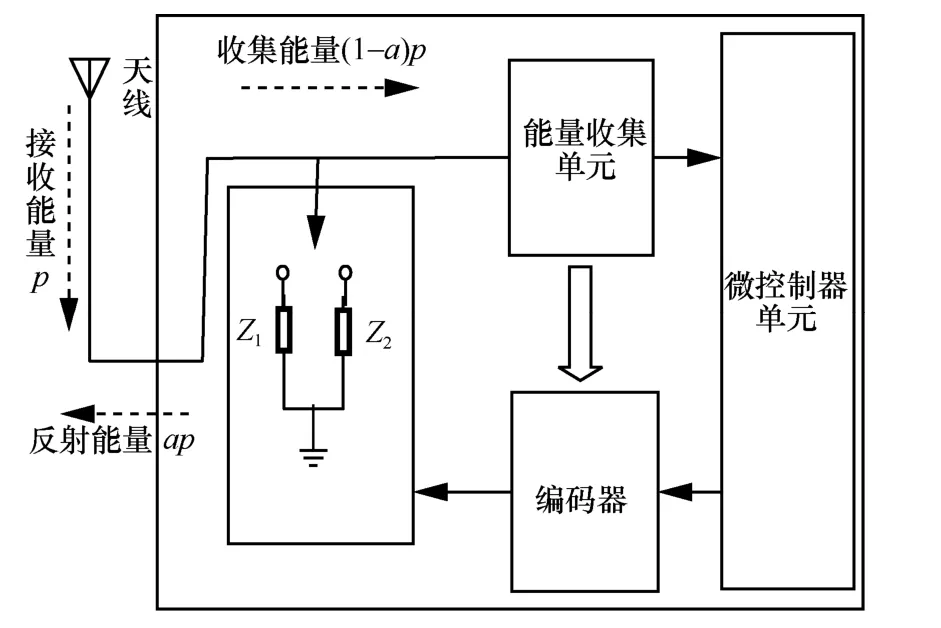
图2 用户的内部结构

其中,等式右边第一项是用户信号经过调制后反射传送至AP 的有用信号,第二项是用户端的背景噪声经过反射传送到AP 的噪声,第三项是AP 端背景噪声。
由于载波信号w在WPBC 系统中一般是已知的,不会对窃听者造成干扰[9],消除这两部分外,窃听者接收到的信号为
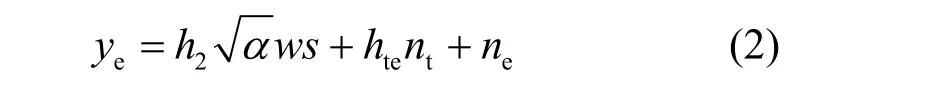
其中,等式右边第一项是窃听者接收的用户信号经过调制后发送至AP 的信号,第二项是用户端的背景噪声经过反射传送至窃听者的噪声,第三项是窃听者端背景噪声。
根据图2 可得,用户收集到的能量为
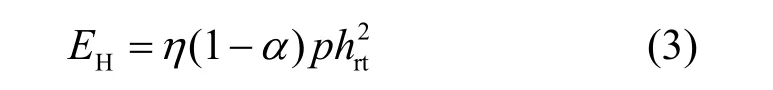
为保证用户正常工作,收集的能量须满足

其中,EC表示用户工作需要消耗的能量,计算式为[28]
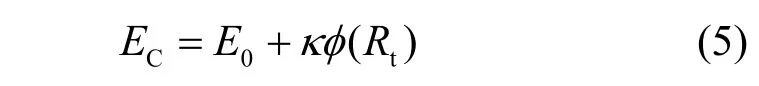
其中,E0和κ均为常数,φ(Rt)表示与数据传输速率Rt相关的功耗,一般取φ(Rt)=Rt[29]。
根据式(1)和式(2)可得,AP 和窃听者接收的信干噪比(SINR,signal to interference plus noise ratio)分别为
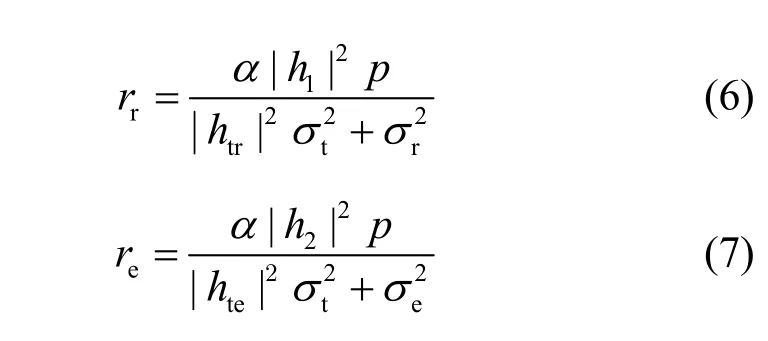
则用户的数据传输速率Rr和窃听者的数据传输速率Re可分别表示为

上述的讨论中,并没有考虑信道估计误差的影响,但是在实际的WPBC 系统中,因为无线信道的随机性,获得完美CSI 的假设过于理想,不满足实际物理通信场景。
综上所述,本文考虑稳健机会约束优化问题,不确定的信道增益由其估计值和加性估计误差组成。因为信道估计误差的存在,在极端情况下可能不满足约束条件,可将问题转化为机会约束问题,允许所做的决策在一定程度上不满足约束条件,但该决策使约束条件成立的概率不小于某一足够小的置信水平。大多数稳健优化的文献在进行系统设计时,都假设信道估计误差服从CSCG 分布[28-30],在采用最小均方误差对信道状态信息进行估计时,信道估计误差将近似满足CSCG 分布[31]。本文考虑信道估计误差服从均值为0 的CSCG 分布的情况,即
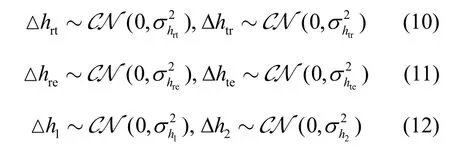
因此,本文的目的是在不超过所允许窃听者最大速率的同时最大化用户需求的最小数据传输速率,其稳健机会约束优化问题可以描述为
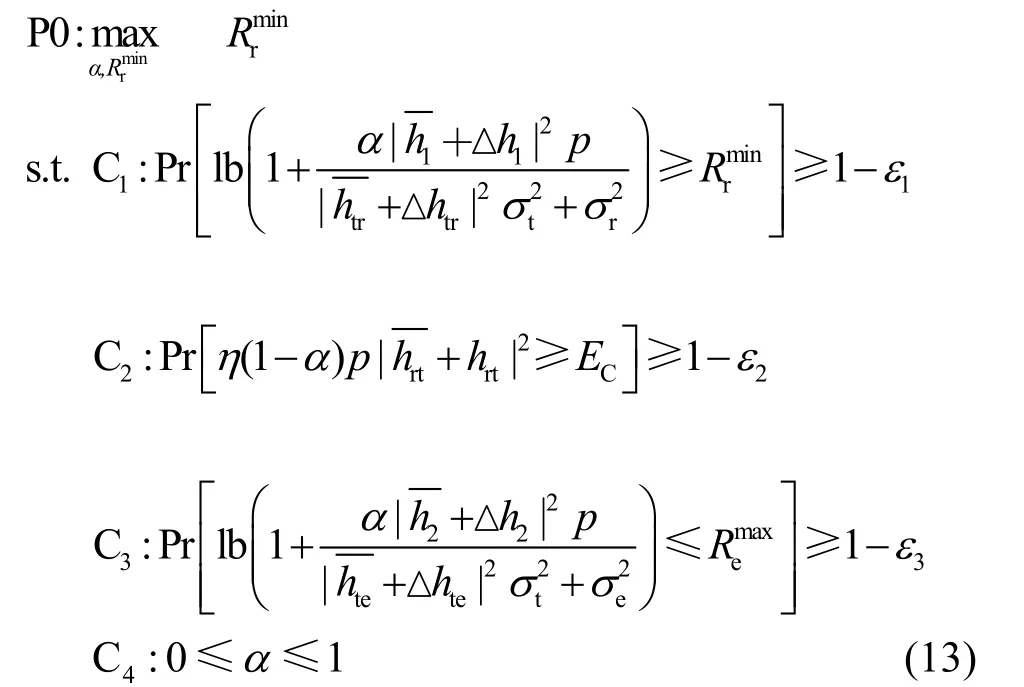
其中,P r[·]表示对应事件发生的概率,ε1、ε2、ε3表示对应事件出错概率的上界。约束条件 C1是用户数据传输速率约束,表示在信道估计误差存在的情况下,用户的数据传输速率至少以1-ε1的概率满足该约束条件。约束条件 C2是最小能量收集约束,表示用户收集的能量大于消耗能量这一事件发生的概率不小于1-ε2。约束条件 C3是窃听者数据传输速率约束,表示存在信道估计误差的情况下,窃听者的传输速率不大于某一常数的概率至少为1-ε3。约束条件 C4表示反射率约束。
3 算法设计
3.1 稳健机会约束优化问题描述与转换
式(13)中包含因信道估计误差而产生的不确定参数,属于机会约束规划的范畴。根据机会约束规划理论可知,机会约束规划的解法大致有2 种。1) 将机会约束规划转化为确定性规划,然后用确定性规划的理论去解决;2) 通过随机模拟技术处理机会约束条件,并利用遗传算法的优胜劣汰,得到机会约束规划的目标函数最优值和决策变量最优解集。本文采用第一种解法,通过伯恩斯坦型不等式的安全近似方法,将原不确定性问题转化为确定性优化问题。
引理1如果Y是复埃米特矩阵,Y∈HN×N,x是服从CSCG 分布的随机向量,x~CN(0,IN),IN表示N阶单位矩阵,u是列向量,满足u∈CN×1,且满足函数关系
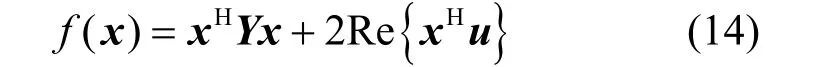
则对于任意非负常数δ>0,有[30]


A1的推导证明见附录1。

详细的推导证明见附录2。
根据引理1,令式(15)中的δ=-lnε1,通过不等式的缩放可得,式(22)是式(17)成立的充分条件。
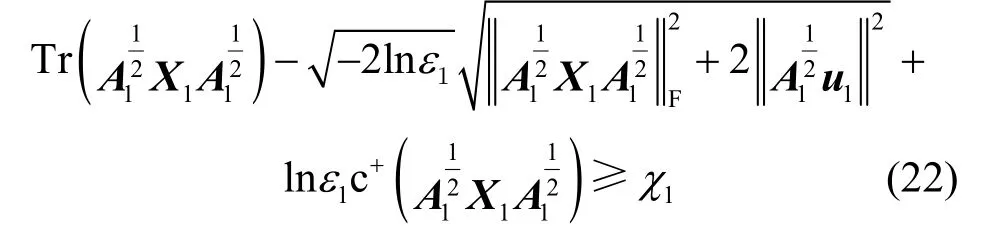
因此,具有机会约束形式的式(17)可以转换为具有确定形式的不等式(22)。
不等式(22)依然含有多个参数且不易处理,引入2 个辅助变量θ1、θ2,根据不等式的性质,式(22)可以进一步转换为
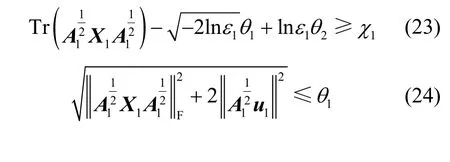
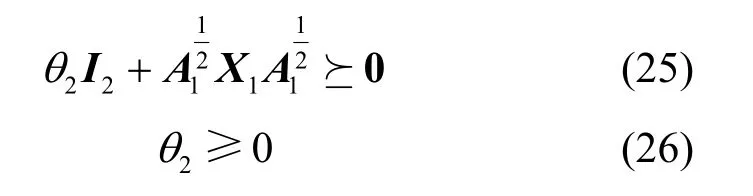
式(24)可以进一步写成二阶锥约束的形式,即

对于约束条件C2,令△hrt=σhrte2,其中e2~CN(0,1),则约束条件 C2可以转换为
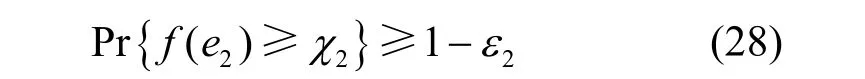
其中,有

根据引理1,条件约束式(28)可以转换为式(33)具有确定形式的不等式
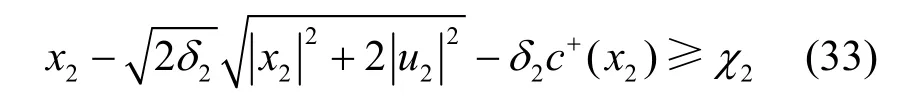
其中,δ2=-lnε2。结合引理1,通过不等式的缩放可得,式(33)是式(28)成立的充分条件。因为式(33)是非线性约束,引入2 个辅助变量θ3、θ4,式(33)可以进一步转换为
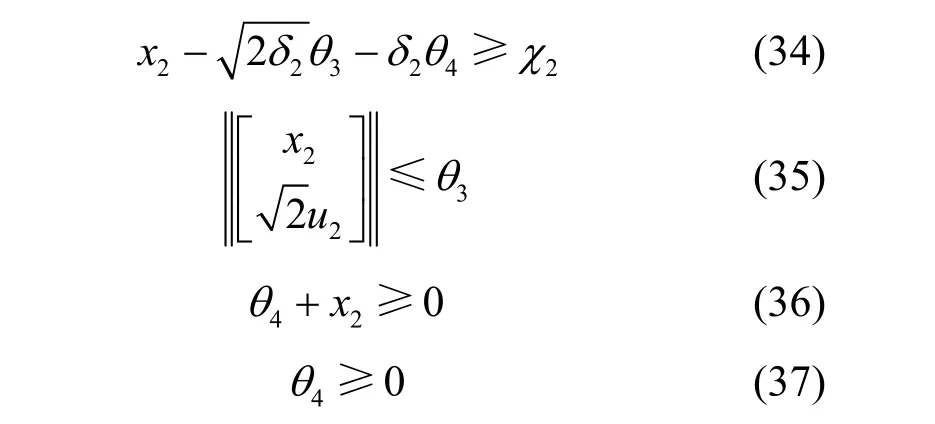
同理,对于约束条件 C3,定义一个信道估计误差向量v3=[Δh2,Δhte]T,v3服从CSCG 分布,满足v3~CN(0,A3),其中,A3表示v3的协方差矩阵,即
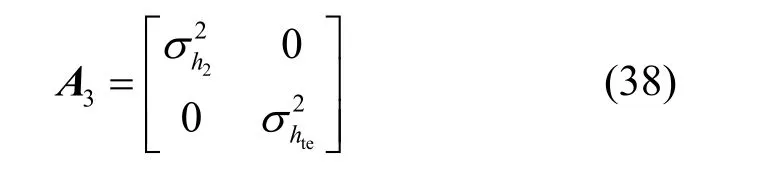
A3的推导证明见附录3。
令v3=,其中e3~CN(0,I2),则约束条件 C3可以转换为
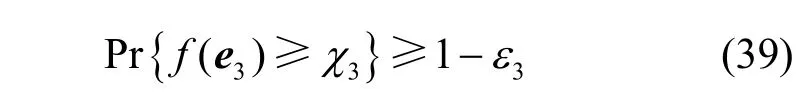
其中,有

详细的推导证明见附录4。
根据引理1,令式(15)中的δ=-lnε3,由不等式的缩放可得,式(44)是式(39)成立的充分条件。
因此,具有机会约束形式的式(39)可以转换为具有确定形式的不等式(44)。不等式(44)依然含有多个参数且不易处理,引入2 个辅助变量θ5、θ6,根据不等式的性质,式(44)可以进一步转换为
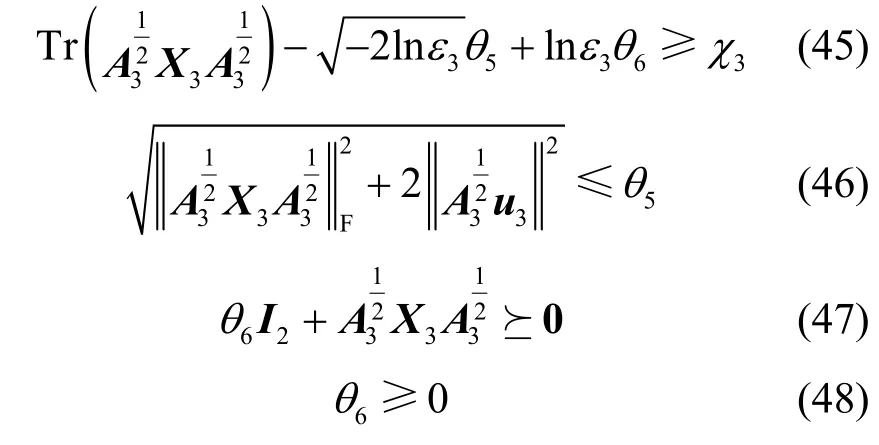
式(46)可以进一步写成二阶锥约束的形式
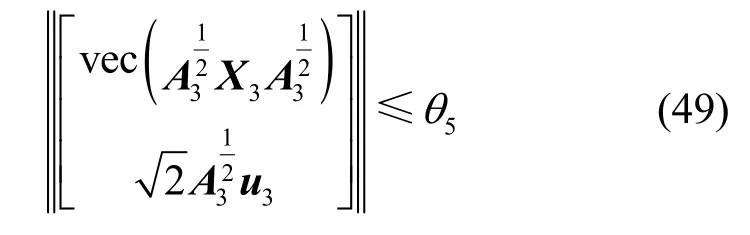
最终,通过利用引理1 中的伯恩斯坦型不等式,把最初的稳健机会约束优化问题P0 转换为容易处理的确定型稳健优化问题P1

其中,约束条件 C5表示反射率约束,约束条件 C6是用户数据传输速率约束 C1的等价转换,约束条件C7是最小能量收集约束 C2的等价转换,约束条件C8是窃听者数据传输速率约束 C3的等价转换。
3.2 稳健机会约束优化算法设计
经过转换之后得到的最终问题P1 是一个凸优化问题,可以利用凸优化工具箱CVX 求解。完整的稳健机会约束优化算法流程如算法1 所示。
算法1稳健机会约束优化算法
1) 形成最初问题P0;
2) 利用引理1,将机会约束1C 转换为确定形式的不等式约束式(22);
3) 利用引理1,将机会约束 C2转换为确定形式的不等式约束式(33);
4) 利用引理1,将机会约束 C3转换为确定形式的不等式约束式(44);
5) 引入辅助变量θ1、θ2,将不等式约束式(22)转换为凸约束式(23)、式(25)~式(27);
6) 引入辅助变量θ3、θ4,将不等式约束式(33)转换为凸约束式(34)~式(37);
7) 引入辅助变量θ5、θ6,将不等式约束式(44)转换为凸约束式(45)、式(47)~式(49);
8) 最终将最初的稳健机会约束优化问题P0 转换为凸优化问题P1;
9) 初始化相应的参数,利用CVX 工具箱求解凸优化问题P1。
3.3 稳健机会约束优化算法动态适配能力分析
本文在第2 节提出了该算法适应的最简单的系统模型,然后对该算法进行了详细的推导和说明,但该算法同样适应于用户较多的传感器网络。
在3 个节点模型的基础上,继续增加节点个数,相比于问题P0,约束条件的个数和约束变量都会相应增加。但是节点个数的增加并没有对算法的基本框架造成影响,仅增加了该算法的时间复杂度以及前期对CSI 估计的工作量[32],该算法依然具有较好的动态适配能力。另外,CSI 估计是由信号接入点完成的,而且信号接入点是有源设备,一般只考虑终端设备的能耗问题,不考虑信号接入点的能耗问题。所以随着传感器节点数量的增加,系统的能量开销会随着CSI估计工作量的增加而相应地增加。
4 仿真结果分析
本文通过MATLAB 仿真平台对所提算法进行仿真,通过仿真结果对所提模型的性能进行分析。
假设能量收集效率系数η=0.6,用户工作需要消耗的能量EC与用户数据传输速率的关系满足功率分别为=10-2W、=10-2W=10-2W。EC=0.3Rr-0.6。AP、用户和窃听者端背景噪声的信道系数采用d-αh,其中α=3表示信道衰落指数,d表示对应设备之间的距离。假设信道估计误差的均方差均为 0.05,即σhrt=σhtr=σhte=σhre=σh1=σh2=0.05。机会约束条件 C1、C2、C3失配的误差上界均设为0.05,即ε1=ε2=ε3=0.05。定义系统的保密率为C=[-Re]+,其中,[·]+=max(·,0)[26]。
为了更好地体现所提算法的效果,在仿真时,将传统的非稳健优化[26]作为一个基准算法进行参考,即直接把估计的信道当作理想信道进行求解。
图3 给出了系统保密率C随信号AP 发射功率p的变化关系。从图3 中可以看出,随着AP 发射功率p的增加,系统保密率C随之增大。因为随着AP 发射功率p的增加,用户可以转化更多的能量来实现更高的数据传输速率。而且,随着AP 发射功率p的增加,用户的数据传输速率的变化要大于窃听者的数据传输速率的变化,从而保证对于窃听者不同的数据传输速率的限制,都能满足对系统保密率的要求。
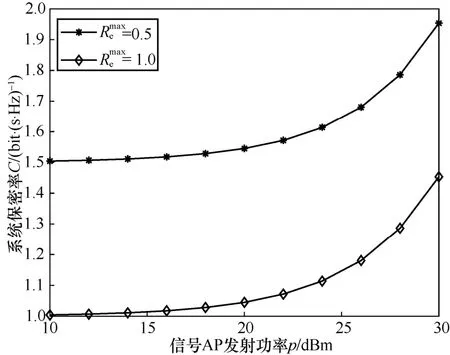
图3 系统保密率C 随信号AP 发射功率p 的变化关系
图4 给出了用户的和系统保密率C与所允许的窃听者最大传输速率的关系。从图4 中可以看出,用户的和系统保密率C均随所允许的窃听者最大传输速率的增加而单调递增,这是因为用户的数据传输速率Rr和窃听者的数据传输速率Re具有相同形式的表达式。Re的增加是由AP发射功率p的变大而造成的,p的增加带来用户的同步增加。从用户的的变化趋势和系统保密率C的取值可以进一步得出,随着所允许的窃听者最大传输速率的增加,用户的会以更快的速度增加,从而保证了系统保密率要求,确保了系统的安全性。
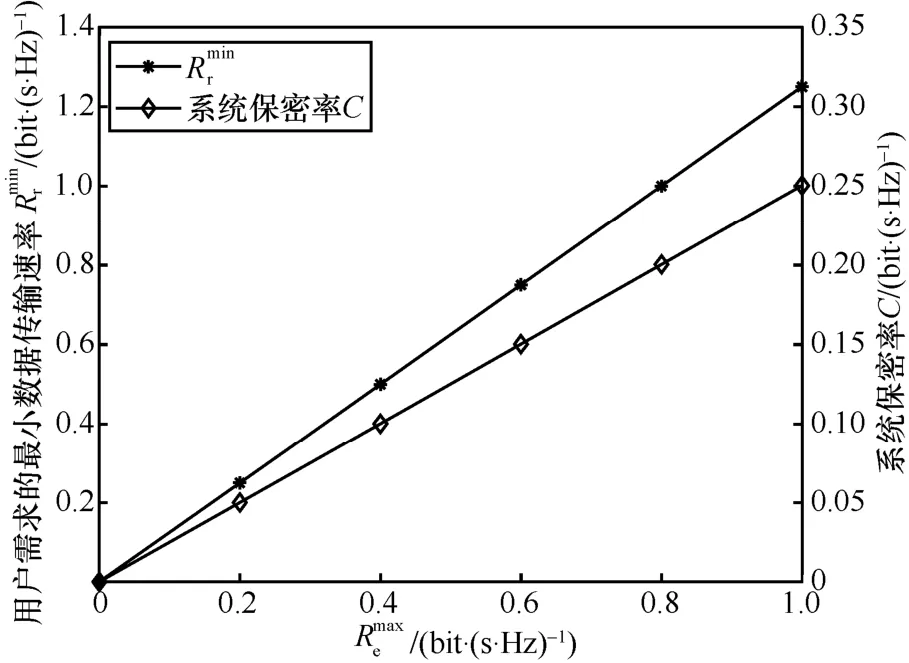
图4 用户的和系统保密率C 与所允许的窃听者最大传输速率的关系
图5 给出了用户的随信道h1估计误差的变化关系。从图5 中可以看出,随着信道h1估计误差的增加,本文算法中用户的随之减小。这是因为信道h1表示信号AP 和用户之间的整个数据传输链路,信道h1估计误差的大小代表了信道估计算法的性能,信道h1估计误差越大,说明信道估计方法得到的信道状态信息和实际信道的状态信息偏差越大,对系统保密率的影响越大。同时,在相同的条件下,通过非稳健优化对应的仿真结果可知,用户的不会随着信道估计误差h1的变化而变化。而且,当信道h1估计误差在可以接受的范围内,本文算法得出的用户的要优于非稳健优化对应的用户的。
图6 给出了用户的随信道h2估计误差的变化关系。从图6 可以看出,随着信道h2估计误差的增加,用户的n随之减小。因为信道h2表示信号AP、用户和窃听者之间的窃听链路,信道h2估计误差的大小反映了信道估计算法的性能,信道h2估计误差越小,说明信道估计方法得到的信道状态信息和实际信道的状态信息越吻合,对系统保密率的影响越小。在相同的条件下,对比非稳健优化对应的仿真结果可以看出,本文算法要优于非稳健优化算法。

图5 用户的随信道h1 估计误差的变化关系
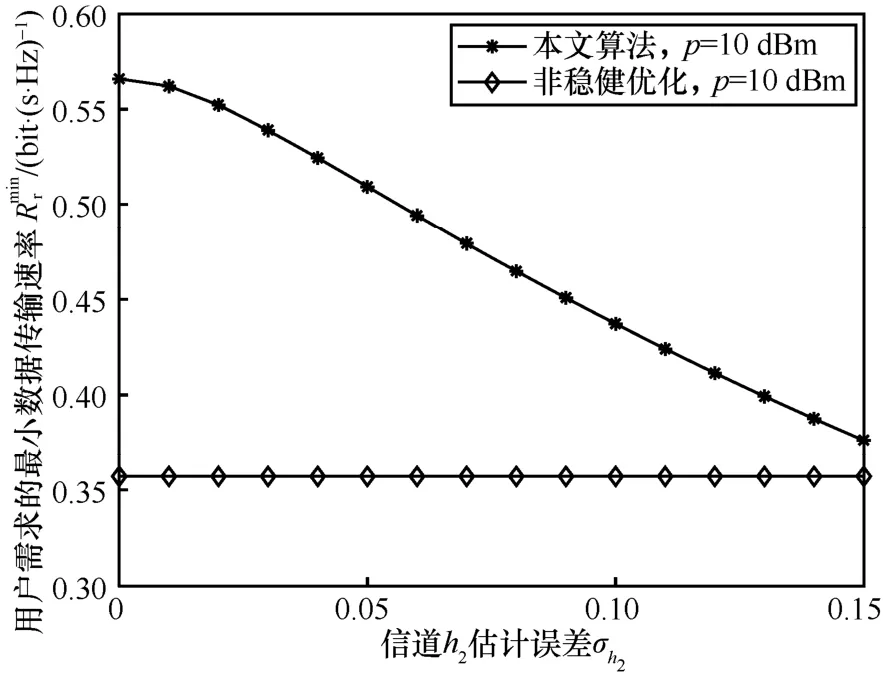
图6 用户的随信道 h2估计误差的变化关系
比较图5 和图6,分析本文算法对应的用户的受信道h1估计误差和信道h2估计误差的影响,可以进一步发现,无论是随着信道h1估计误差的增加,还是信道h2估计误差的增加,用户的都呈下降趋势。造成这一结果的主要原因是无线信道是随机变化的,无论在实际中采用什么信道估计方法,都不能做到完全消除误差,只能将误差降低到可以接受的范围。虽然受2 种信道估计误差的影响,系统的保密率都呈下降趋势,但是2 种变化趋势对应的变化率存在明显的差别,用户的受到数据传输链路h1估计误差的影响比受到窃听链路h2估计误差的影响更大,所以在实际应用中将信道估计误差考虑在内更加合理。这一对比结果说明了通过克服信道不确定性、提高网络稳健性,可以达到安全通信的目标。
5 结束语
本文对基于无线供能的BCS 的安全性进行研究。考虑用户与窃听者的传输速率约束、最小能量收集约束和设备反射率约束,建立基于信道不确定性的稳健机会约束优化模型。利用伯恩斯坦型不等式的安全近似方法,将优化问题中的机会约束条件转换为确定形式的不等式约束,将原问题转换为确定性的优化问题;根据不等式的性质,引入辅助变量,将该问题转换为凸优化问题,利用CVX 工具箱获得了最初问题的解。通过仿真得出,所提的稳健优化算法明显优于非稳健优化算法。而且可以发现,在现实存在信道估计误差的场景中,信道估计误差会对系统性能造成影响。所提算法考虑WPBC,将WPCS 和BCS 结合,实现低功耗通信,来解决IoT中能量短缺问题,当传感器节点数量较多时,该算法能够动态适配。同时所提算法将信道的不确定性联合传输速率进行考虑,较好地解决了信道状态信息失配和窃听者同时存在的安全通信问题。
附录1 式(16)的证明
A1表示v1的协方差矩阵,其中v1=[△h1,△htr]T,由协方差矩阵的定义可知
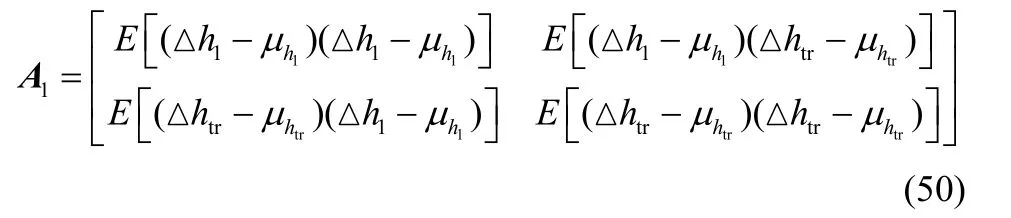
其中,协方差公式为
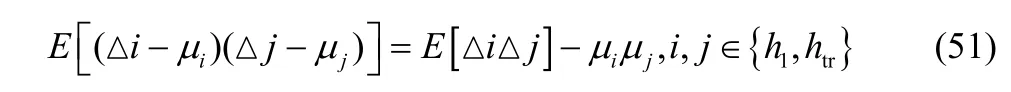
根据式(10)和式(12)可知,μh1=μhtr=0,因为变量的二阶原点矩等于其对应的方差,所以A1的主对角线元素就是对应变量的方差,即。因为信道h1和信道htr的估计是相互独立的,所以其信道估计误差信道△h1和△htr也是相互独立的,因此A1的副对角线元素都是0。由以上推导可得
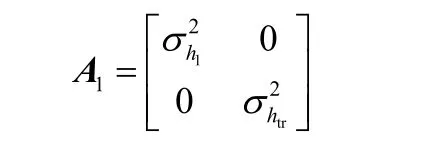
证毕。
附录2 式(17)的证明
为了方便讨论,使用一阶泰勒展开式对约束条件1C 进行展开可得
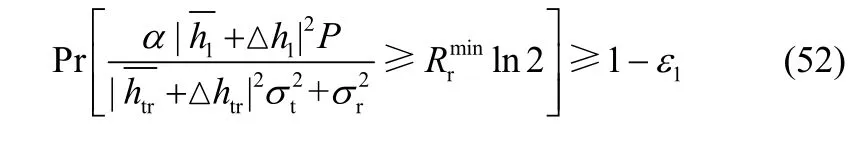
其中,有
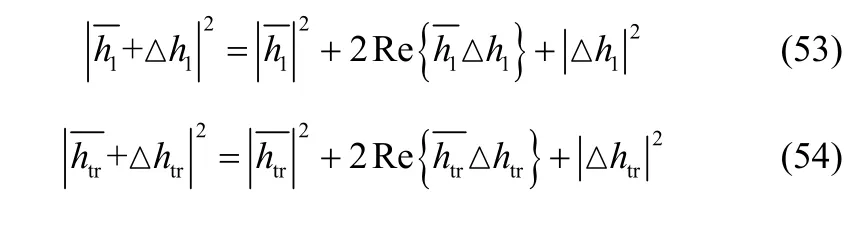
根据二次型和矩阵的对应关系,任意给定一个向量x=[x1,x2],则含有变量x1,x2的二次齐次函数为
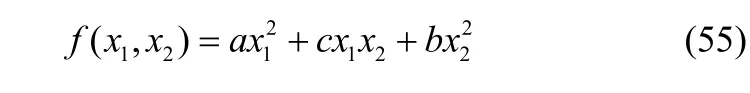
可以用矩阵的形式进行表示,即

其中,
称为该二次型对应的矩阵。
基于以上的知识,可以推导出式(17)及相关参数。证毕。
附录3 式(38)的证明
A3表示v3的协方差矩阵,其中v3=[△h2,△hte]T,由协方差矩阵的定义可知
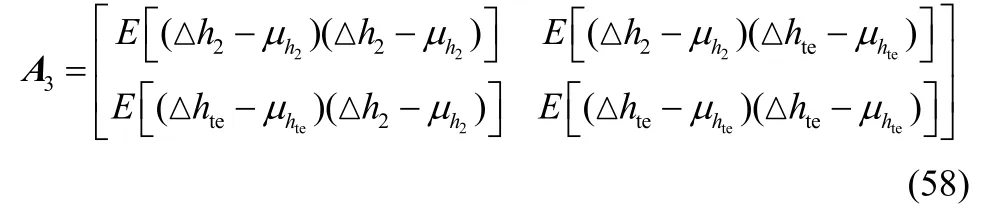
其中,协方差公式为
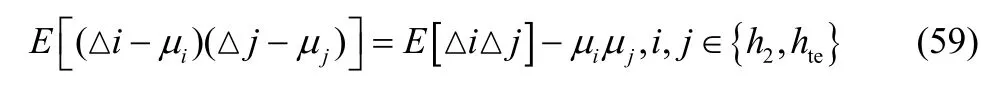
根据式(11)和式(12)可知,μh2=μhte=0,因为变量的二阶原点矩等于其对应的方差,所以A3的主对角线元素就是对应变量的方差,即。因为信道h2和信道hte的估计是相互独立的,所以其信道估计误差信道2h△ 和△hte也是相互独立的,因此A3的副对角线元素都是0。由以上推导可得

证毕。
附录4 式(39)的证明
为了方便讨论,使用一阶泰勒展开式对约束条件C3进行展开可得
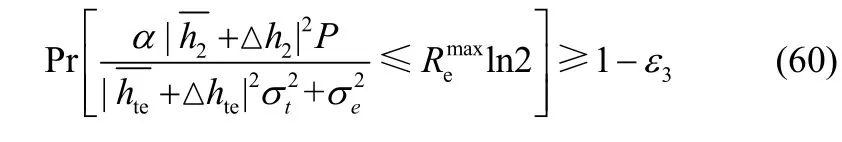
其中,有
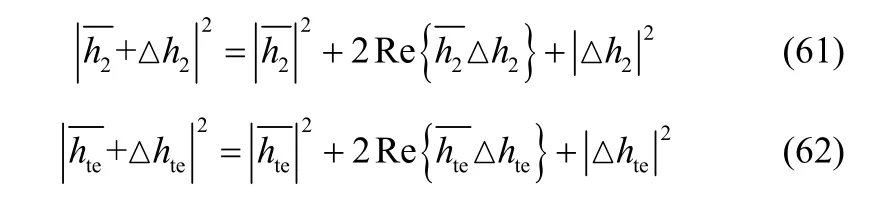
根据二次型和矩阵的对应关系,任意给定一个向量x=[x1,x2],则含有变量x1,x2的二次齐次函数为
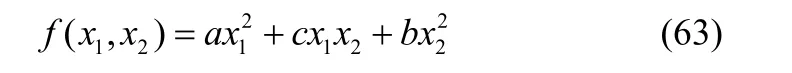
可以用矩阵的形式进行表示,即

其中

称为该二次型对应的矩阵。
基于以上的知识,可以推导出式(39)及相关参数。证毕。
