木结构燕尾榫节点应力分析研究*

张 俊 李源河 李英洁 徐伟涛 姚利宏

（1.内蒙古农业大学材料科学与艺术设计学院，内蒙古 呼和浩特 010018; 2.国家林业和草原局林产工业规划设计院，北京 100010)

木结构古建筑是一种以木构架为承重系统，墙体作围护结构的建筑[1]。榫卯节点是木构架的主要连接方式，其柱端与梁端分别制成卯口和榫头形式，将梁端的榫头插入柱顶预留卯口中[2]，形成一种凹、凸结合的特殊结构系统。在地震荷载下，榫卯节点多通过节点间摩擦滑移与挤压进行消震减震，是木结构耗能的主要部位[3-4]，具有一定的拉伸、压缩、弯曲和抗扭强度和半刚性特点[5-7]，其对木结构建筑整体稳定性起着至关重要的作用。

燕尾榫有“万榫之母”之称，是梁柱构件典型的节点连接形式之一。李义柱[8]试验发现燕尾榫节点的刚度与节点转角成反比，弯矩与节点转角成正比，其滞回环形状均呈反Z形，具有显著的“捏拢”和“滑移”效应。周乾等[9]对比燕尾榫与直榫发现，两者卯口处都有不同程度拉、压、剪破坏，且燕尾榫更为严重，榫头更易破坏。张令心等[10]发现燕尾榫节点榫颈与卯口处最易发生破坏，木材的材性和节点的形状均会影响破坏的形式。杨娜[11]首先构建了燕尾榫节点初始刚度与极限弯矩的回归模型，并依此推导出古建筑木结构整体结构计算的燕尾榫节点三参数幂函数模型。吴洋等[12]发现燕尾榫底部受力最为集中，额枋两端受力相对薄弱，拔榫是燕尾榫主要的破坏形式。罗勇[13]得到了准确的燕尾榫木构架弯矩-转角滞回曲线。本文在已有燕尾榫节点受力研究基础上，从模型比例与等材方面展开研究，利用ABAQUS对其进行拔榫量与应力分析，以期为后续燕尾榫节点受力分析研究提供参考。

1 燕尾榫节点受力机理

在燕尾榫节点连接梁枋时，因其限制了沿榫宽和榫深方向的自由度，只允许沿榫厚方向的移动，因此具有良好的接合强度。本文利用ABAQUS有限元分析软件模拟不同等材与不同比例的燕尾榫节点，分析其在单调加载和低周循环往复加载下的力学性能。

如图1 所示，假定燕尾榫节点向下转动为正方向[14]。榫头沿着榫颈转动时，由于上部与卯口挤压，受到来自卯口的压应力N2，同时还受到来自卯口与榫头上表面间的反向摩擦力f。榫头下部正向转动时，相对卯口滑移量较少，摩擦力可忽略不计，主要受与卯口之间(垂直于枋长方向)的斜向合力N3[15]。

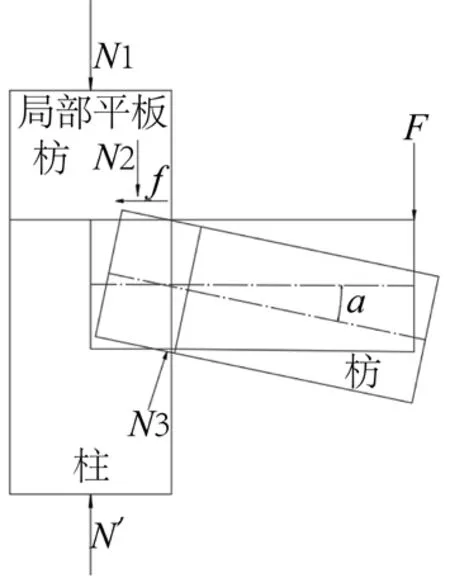
图1 燕尾榫节点加载受力示意图Fig.1 Schematic diagram of the stress on the dovetail joint

2 有限元模型建立

2.1 木材材性定义

木材顺纹本构模型和横纹本构模型分别如图2a、b所示，其中横纹本构模型考虑了弱强化段[16]。图中εcu为木材顺纹极限压应变，εco为木材顺纹受压屈服应变，εtu为木材顺纹受拉屈服应变，Ecs为木材顺纹受压弹性模量，Ets为木材顺纹受拉弹性模量。εL为木材横纹受压屈服应变，εN为木材横纹受压极限应变，E1为木材横纹受压弹性段模量，E2为木材横纹强化阶段的受压弹性模量，σL为木材的横纹受压强度，σN为木材横纹强化段结束时的受压强度。

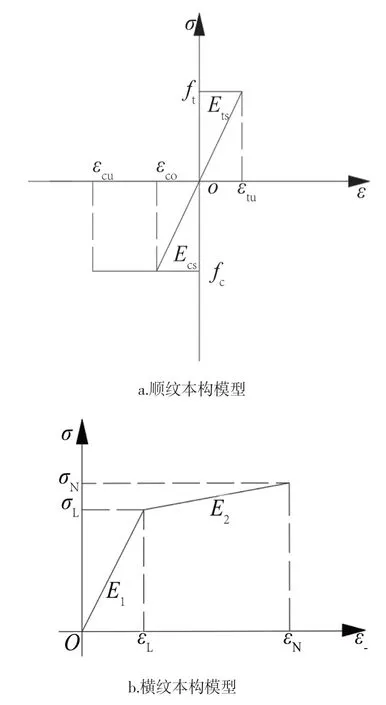
图2 木材本构模型Fig.2 Constitutive model for wood

ABAQUS软件中木材弹性特征用工程弹性常数来定义。本次模拟试验选择樟子松材（Pinus sylvestris）为研究对象，其弹性工程常数见表1[17]。

表1 樟子松弹性工程常数Tab.1 Engineering constants of Pinus sylvestris var. mongolica Litv.

2.2 节点模型建立

依照《营造法式》“材分制”标准[19-20]，设计了模型比例1∶3.2、1∶2.2、1∶4.4的二等材燕尾榫节点（依次命名为YS-1、YS-2、YS-3）与模型比例1∶3.2三等材燕尾榫节点（YS-4）。燕尾榫节点缩尺模型尺寸通过现代国际基本单位与宋尺转换得出，节点尺寸示意图如图3所示。

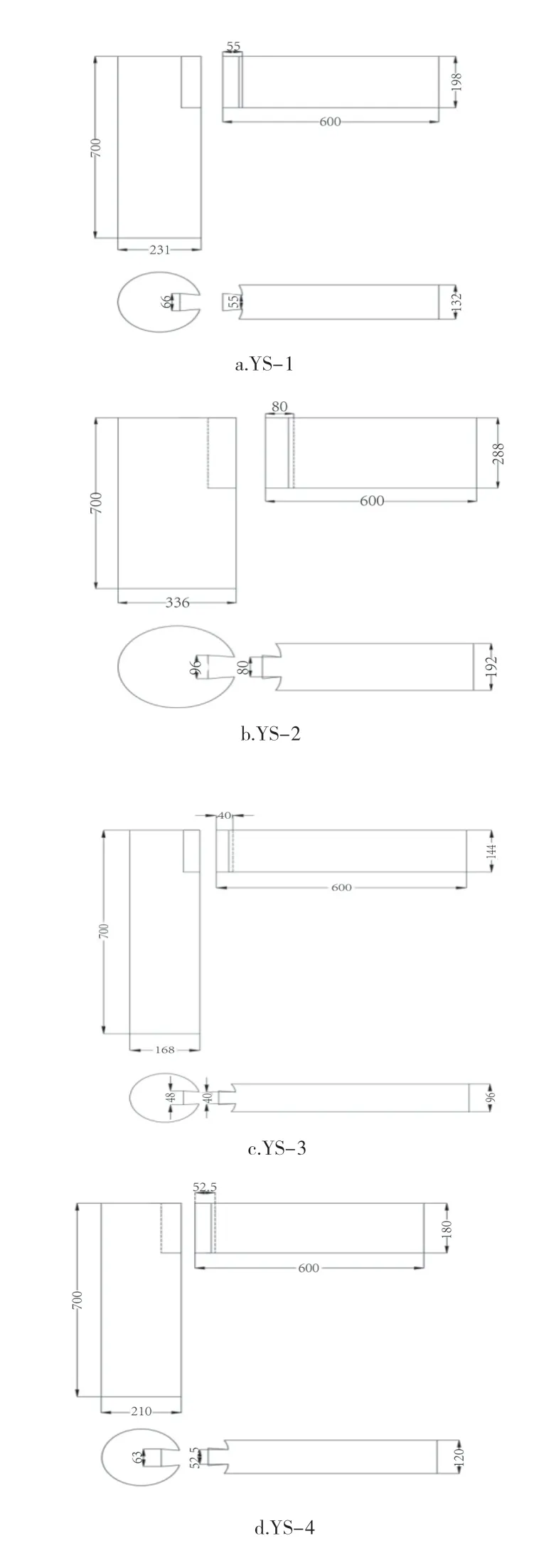
图3 燕尾榫节点尺寸示意图Fig.3 Dimensional diagram of dovetail joint

2.3 摩擦参数定义

燕尾榫节点的榫头与卯口接触面上存在切向和法向作用。接触面之间为法向作用时，定义接触方式为“硬接触”[21]，不限制榫卯节点接触面间的压力。当两接触面相互分离压力为零时，作用其面上的接触约束被解除。接触面之间为切向作用时，榫卯节点接触面产生摩擦力。由于在柱顶局部平板枋施加了轴向均布荷载，为了保持局部平板枋与柱接触，因此两者之间采用绑定连接[22]。榫头与卯口部位，选择柱端卯口作为从面，榫头作为主面；柱顶端面与局部平板枋接触部位，主面选择柱顶端面，从面选择局部平板枋接触底面。

2.4 网格与单元定义

采用C3D8R（三维八节点六面体单元）与Hex扫掠网格划分机制对燕尾榫节点模型进行网格划分与单元定义[23-24]，对枋、柱与局部平板枋分别选取44、34 mm与24 mm网格进行划分。采用这种网格优点是运算精度高，位移求解结果精准，当网格出现变形扭曲问题时对分析精度影响较小，弯矩作用时一般不会发生剪切自锁。

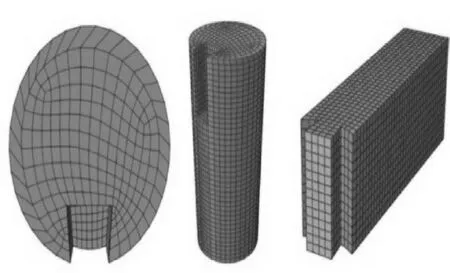
图4 燕尾榫节点网格划分Fig.4 Meshing of dovetail nodes

2.5 边界条件定义与载荷施加方式

根据燕尾榫节点实际受力情况，对立柱采用一端固结，另一端铰接的边界条件。模型中柱顶部分在x、z方向施加位移约束，y、z方向施加转动约束；柱脚施加x、y、z方向的位移约束与y、z方向转动约束，使其位移和转角均为0。为防止柱顶截面出现应力集中现象，将柱顶轴向载荷转化为均布载荷。节点边界条件定义与施加载荷方式如图5所示。

模型通过3个分析步来实现加载：初始步为定义边界条件；接触步考虑计算结果的收敛，在枋端施加小段位移，使榫头与卯口无缝接触；分析步对枋施加单向载荷与低周往复循环载荷[25]。

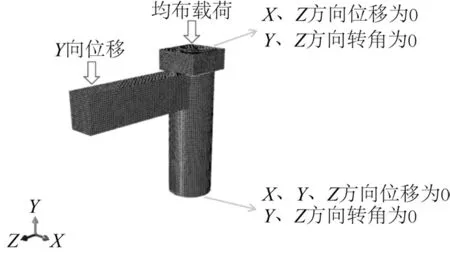
图5 边界条件与载荷施加方式Fig.5 Boundary conditions and loading methods

3 结果与分析

3.1 拔榫量

随着控制位移的增加，榫头与卯口发生挤压变形，导致节点松动，榫头逐渐拔出卯口。当拔榫量超过一定限度时，节点失去承载能力甚至脱榫，严重影响结构的稳定与安全。图6为YS-1、YS-2、YS-3、YS-4在 0.08 rad转角时的榫头拔榫量。

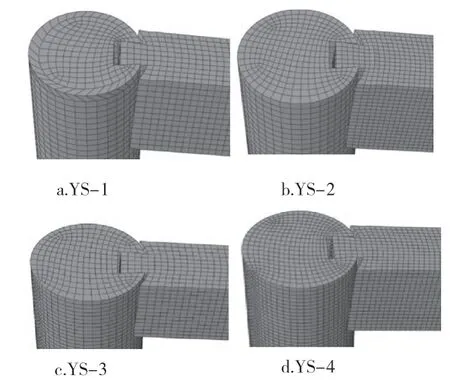
图6 燕尾榫节点拔榫量示意图Fig.6 Dovetail joint drawing

由图7可知，YS-1、YS-2、YS-4在第一级控制位移下的拔榫量较为接近，均为1.76 mm左右，YS-3拔榫量明显较小，其值为0.66 mm。YS-1、YS-2、YS-3与YS-4在最后一级控制位移下的最大拔榫量分别为13.5、17.8、4.9 mm与11 mm，表明模型比例越大拔榫量越小，且同模型比例下二等材节点榫头拔榫量大于三等材节点。

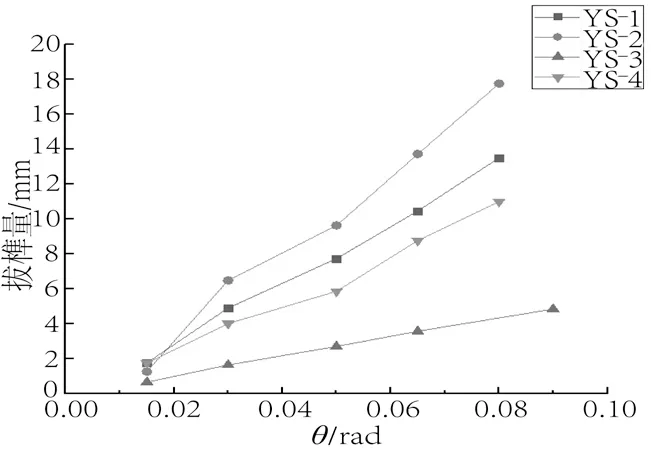
图7 燕尾榫节点拔榫量-转角关系Fig.7 Dovetail joint pull-out angle relationship

3.2 应力

由于木材是一种各向异性材料，应建立木材的三维坐标系，并定义榫卯节点的顺纹与横纹方向。本文规定S11为顺纹方向应力，此方向榫头分上下两侧，其中一侧受拉，一侧受压；S33为横纹（径向）方向应力，榫头沿右上和左下方向受到来自卯口的压应力。

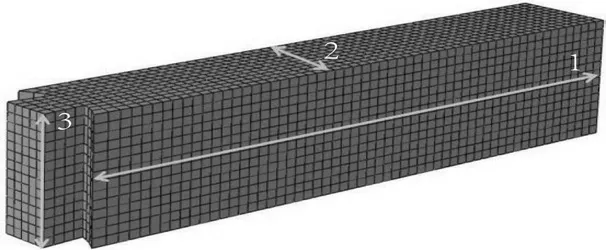
图8 榫头的顺纹与横纹方向Fig.8 The direction of the lines and lines of the tenon

3.2.1 顺纹方向

YS-1、YS-2、YS-3 与YS-4 在0.015、0.035、0.05、0.065rad和0.08rad时的应力云图如图9 所示。当节点向右加载时，榫头沿顺纹方向左侧受拉，右侧受压，颜色越深表明受力值越高，且拉力与压力值随着转角的增大而增加。在0.08rad时YS-1 拉应力与压应力分别为9.3MPa与18.2MPa，YS-2 拉应力与压应力分别为10.5MPa与14.4MPa，YS-3 拉应力与压应力分别为9.1MPa与13.6MPa，YS-4 拉应力与压应力分别为13.9MPa与17.8MPa，可见压应力明显大于拉应力。通过应力云图也可观察到0.08 rad时榫头左侧榫额与榫头右侧榫颈处已经屈服。但拉压应力均未超过木材顺纹抗拉抗压强度，即未达到破坏阶段。

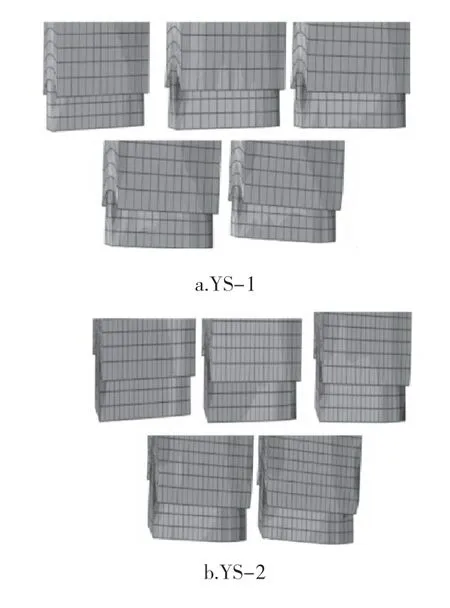
图9 燕尾榫节点榫头S11 应力云图Fig.9 S11 stress contour of dovetail joint tenon

3.2.2 横纹径向方向

YS-1、YS-2、YS-3 与YS-4 在0.015、0.035、0.05、0.065rad和0.08rad时的应力云图如图10 所示。当节点循环加载时，S33应力受力形式为：榫头左下部和右上部受到来自卯口横纹径向方向的压应力，且压应力与变形量随转角的增大而增加。在0.08rad时YS-1榫头左下部和右上部所受的压应力分别为4MPa与6MPa，YS-2 榫 头 压 应 力 分 别 为4.7 MPa与5.8MPa，YS-3 榫头压应力分别为3.5MPa与4.1MPa，YS-4 榫头压应力分别为5 MPa与4.9MPa。只有YS-3 榫头左下部与右上部应力值均未超过木材横纹径向抗压强度（4.55MPa），YS-3 沿横纹径向没有出现明显的塑性变形。

图10 燕尾榫节点榫头S33 应力云图Fig.10 S33 stress contour of dovetail joint tenon

3.2.3 剪应力

由于剪应力也是随着转角的增大而增加，因此直接取节点0.08 rad时的最大剪应力进行对比。由图11可得，榫头与榫颈的剪应力方向相反，榫头与榫颈两侧均承受较大的剪力。YS-1、YS-2、YS-3 与YS-4 的最大剪应力分别为2.5、2.9、1.8MPa与3.0MPa，均未超过极限剪应力。因此，加载过程中未发生木材材料剪切破坏。

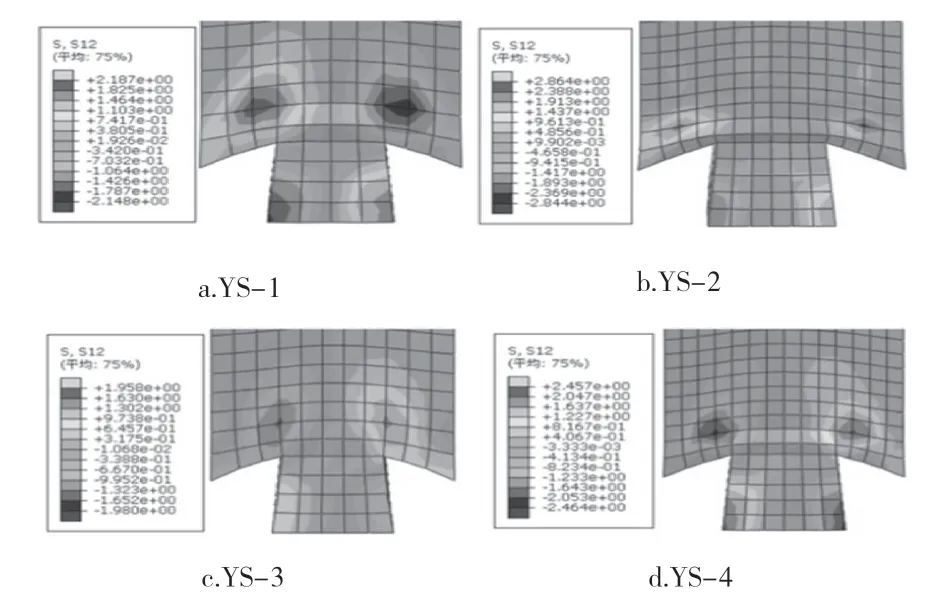
图11 燕尾榫节点榫头S12 应力云图Fig.11 S12 stress contour of dovetail joint tenon

3.2.4 榫头等效塑性应变

榫头等效塑性应变（PEEQ）是指榫头在循环控制位移加载中，所受的拉伸和压缩应变绝对值的和。由图12 可以看出，在0.08 rad时榫颈已经发生了非常明显的塑性变形，随着加载位移级数的增加，榫头的挤压与塑性变形也愈发明显。PEEQ值呈线性增长，在榫头端部的PEEQ值最小，榫颈处PEEQ值达到最大。

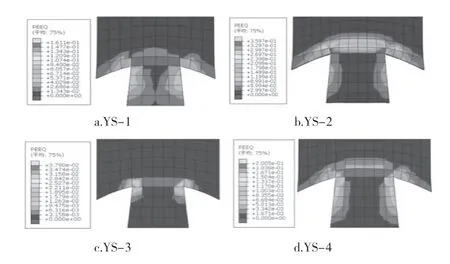
图12 燕尾榫节点PEEQ应力云图Fig.12 PEEQ stress cloud diagram of dovetail joint

4 结论

燕尾榫节点的榫头拔榫量随模型比例增加而减小，同模型比例下二等材节点的榫头拔榫量大于三等材节点。YS-1、YS-2、YS-3 与YS-4 的拉应力和压应力均未超过木材顺纹极限抗拉与抗压强度。YS-1、YS-2 与YS-4 榫头左下部和右上部横纹方向所受压应力均超过横纹径向抗压强度，即节点进入了二次强化阶段；YS-3 榫头未超过木材横纹径向抗压强度，因此该节点未产生明显塑性变形。4 个节点所受剪应力均未超过极限剪应力，因此节点未发生木材材料剪切破坏，而榫头端部的PEEQ值最小，榫颈处PEEQ值最大。