基于单变量函数分解的结构区间静力响应分析

魏彤辉 孟广伟 左文杰 李锋

(吉林大学 机械与航空航天工程学院，吉林 长春 130025)

在实际工程中，设计参数的名义值总是受到一定程度的不确定性影响。为了能够对工程系统进行真实可靠的评估，人们在数值模拟中引入了不确定性分析[1- 2]。概率论是处理参数不确定性的传统方法，它利用采集到的统计数据来证明所假设的统计分布，若分布概型推断错误，则将使计算结果产生较大误差。在这种情况下，可以使用非概率方法来量化和处理不确定性。非概率方法中的区间集发展多年，理论比较完备，常被用来描述不确定性[3]。区间集是将参数的不确定性引入区间数，即已知不确定变量位于两个规定的边界之间，但不假设区间内的统计分布。因此，当不确定参数的变化范围已知，且可用信息不足以确定该范围内的分布类型时，宜采用区间集来处理不确定性。

近年来，学者们提出了许多区间分析方法来求解结构的静态响应，包括顶点法[4- 5]、区间配置法[6- 7]、区间摄动法[8- 13]等。例如，Qiu等[4]利用克拉默规则和凸集理论给出了顶点解定理的证明方法，并扩展了这一定理来进行结构的静力分析[5]。众所周知，随着区间刚度矩阵单元数的增加，顶点法的计算速度呈指数增长，这对于大型结构是不可接受的。Wu等[6]利用切比雪夫多项式级数提出了一种新的区间分析方法，用于计算非线性动力系统的响应边界。Liu等[7]提出了一种贝叶斯配置方法，用于含有界但未知不确定参数的结构静力分析。这两种方法从本质上来说，均是一种代理模型，并且适用于线性和非线性结构系统，但是为了满足一定的精度要求，通常需要大量的样本点，尤其当区间参数较多时，其计算成本呈指数增长。

为了提高含大量区间参数的静力结构的计算效率，Chen等[8]利用摄动技术和区间扩展进行了区间静力位移分析。随后，吴杰等[9]基于一阶Taylor展开法与区间数学，将静力和动力学响应区间优化问题转化为一个确定性优化问题。受到文献[8]的启发，Xia等[10]提出了改进的一阶区间摄动有限元法，并将其推广到声场和声固耦合问题的声压响应预测上。上述的区间摄动法都只考虑了一阶摄动近似，但一阶区间摄动法在大不确定度区间变量下很难达到预定的精度，甚至会因为线性近似使响应结果失真，而改进的一阶区间摄动有限元法在不确定参数增多时的计算效率又太低。有鉴于此，Chen等[11]基于二阶Taylor展开与区间运算求解了结构静态响应区间的上、下界；Fhjita等[12]在求解二阶Taylor展开摄动量时，考虑了目标函数在不确定变量区间内的极值点；尹盛文等[13]在二阶Taylor展开的基础上推导了声学二阶区间摄动有限元法。但对于高阶非线性的区间函数，二阶Taylor展开的计算精度仍得不到保证，而且在计算效率方面也不再具有优势。

可以看出，上述文献在提高计算结果的准确性和计算效率方面做了大量的工作，但是大多数的理论研究忽略了计算效率和结果准确性之间的平衡。例如，现有的顶点法[4]和区间配置法[6]通常需要大量的样本计算，而基于低阶Taylor展开[8，11]的区间有限元法因其高阶项被忽略，最高只包含Taylor级数的前二阶项，但对于强非线性函数，高阶项对结构响应有着非常重要的影响，这就将区间有限元法的应用限制在了一个小的不确定度范围内。另外，在求解结构响应时需要对响应函数求导，而强非线性函数的求导较困难，甚至无法求导。

综上，文中提出了单变量函数分解区间有限元法——首先利用高阶Taylor展开得到单变量函数分解的区间表达式，将n维结构响应函数展开成含n个一维函数的和函数；然后将区间变量的端点值代入近似响应函数，最终得到结构静力位移响应的上、下界。

1 问题描述

结构系统静力学的有限元控制方程为

Ku=F

(1)

式中：K∈Rn×n，为总体刚度矩阵；u∈Rn×1，为结点位移向量；F∈Rn×1，为载荷向量。由于制造缺陷、测量误差和载荷波动等原因，很多情况下，结构的物理和几何属性存在不同程度的不确定性。

假设结构参数向量α是不确定的，根据区间数学中的区间向量记法，有

(2)

(3)

(4)

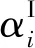
(5)

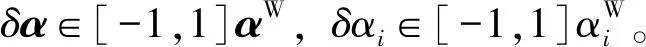
(6)

在现有不确定性信息的基础上，将所有的不确定参数视为不确定但有界(或区间)的参数。在这种情况下，结构刚度矩阵和载荷向量都是区间不确定向量αI的函数，式(1)可写成如下形式：

K(αI)u=F(αI)

(7)

易知，结点位移向量u也是αI的函数。因此，具有区间参数的精确结构静态位移是一个集合，可表达为

Ω=u(αI)={u：u∈Rn，K(α)u=F(α)，∀α∈αI}

(8)

原则上，集合Ω是由Moore等[14]定义的非凸多面体，这使得极难获得式(8)中解集的确切特征。在实际工程中，工程师们感兴趣于结构响应的边界，因此，一项重要的工作是预测静态位移的上、下限，其定义为

(9)

由式(9)给出的响应边界，可以很容易地判断结构响应的界限。但是不确定参数和结构响应之间的映射通常是非常复杂或不可知的，为了得到计算结果，将调用大量的有限元做确定性分析，这在实际工程中将非常昂贵且难以处理。为了减少计算量，同时确保结果的准确性，学者们提出了一些方法，其中基于低阶Taylor展开的方法[5，13，15- 16]已被应用于实际工程，且取得了良好的效果。

2 区间摄动有限元法

2.1 一阶区间摄动有限元法

根据式(7)给出的区间有限元方程，计算得位移响应如下：

u(αI)=K-1(αI)F(αI)

(10)

对位移响应u(αI)在区间中点αC处进行一阶Taylor展开：

(11)

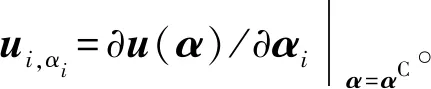
(12)

(13)

式中，eΔ=[-1，1]。基于一阶Taylor展开的线性近似，可得位移响应的最大和最小值分别为

(14)

2.2 二阶区间摄动有限元法

为了提高计算精度，将二阶Taylor展开引入区间位移分析。对u(αI)在区间中点进行二阶Taylor展开：

(15)

式中，G(αC)和H(αC)分别为梯度向量和Hessian矩阵在区间中点αC的取值，相应的G(αC)和H(αC)可分别表示为

(16)

(17)

其中∂2u(αC)/(∂αi∂αj)为响应函数对区间变量的二阶偏导数。将式(12)两边关于αj求微分，可得

(18)

对于n维区间变量，H(αC)为n维方阵，当不确定变量总数n较大时，其计算成本很高。为了简化计算和提高计算效率，Chen等[11]只考虑了Hessian矩阵的对角元素，将位移响应近似为

(19)

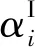
(20)

将式(20)代入式(19)，可得

(21)

根据式(21)，在变化区间αI内，n维位移响应的上、下界可表示为

(22)

3 基于单变量函数分解的区间有限元法

式(11)和(15)最高只包含Taylor展开的二阶项，忽略了高阶项，而高阶项对强非线性函数有很重要的影响。假设响应函数在区间参数向量的中点有一收敛的Taylor级数[17]，那么，u(αI)可表示为

(23)

(24)

同理，可以得到其他单变量的Taylor展开式：

(25)

然后，将式(24)和(25)求和，得到单变量函数的和表达式为

(26)

再对式(26)进行移项，可以得到

(27)

最后，将式(27)代入式(23)并忽略残余项R2，可以得到响应函数的单变量函数分解表达式：

(28)

可以发现，u1(αI)与真实响应u(αI)的误差为R2。此外，与一阶Taylor(式(11))和二阶Taylor(式(15))相比，u1(αI)包含了低阶Taylor展开式中单变量的所有高阶项。

对式(28)进行区间展开，可得u1(αI)的上界和下界如下：

(29)

式(29)中，u1(αI)在不确定域中任意点的响应近似由其n个一维子函数的值计算得到，且n为大于1的整数。同时，每个子函数只包含一个不确定参数，其他参数则用其中点值代替。

假设存在n个区间变量，且u(αI)是单调的，则可通过将区间变量的端点和中点代入式(29)来计算u(αI)的边界，由此式(29)可改写为

(30)

因此，文中方法仅需进行2n+1次确定性分析就可得到u(αI)的边界值。图1给出了n=2时文中方法所需全部样本点的分布示意图。与常用作单调区间响应精确解的顶点法相比，文中方法的样本数呈线性增长，而顶点法则为指数增加。

图1 n=2时文中方法的样本分布

可以看出，式(30)的应用前提是结构响应具有单调性，对于非单调的函数，可以在单变量函数分解的基础上，结合子区间法[18]等方法进行求解。

4 测试函数

为了证明文中方法可高效且准确地求解高维强非线性函数，列举如下的含8个不确定参数的区间算例：

(31)

在本算例中，令8个不确定参数的区间范围相同，均为[5-5×λ，5+5×λ]，其中λ为式(6)所定义的相对不确定度。在区间分析中，扫描法常被视作单调和非单调响应函数的精确解(Exact)[6]，因此本算例利用扫描法得到Exact。为了叙述方便，将一阶和二阶区间摄动有限元法、基于单变量函数分解的区间有限元法分别简写为IFE-first、IFE-second 和IFE-ufd。当λ为0.3时，利用Exact、IFE-first、IFE-second和IFE-ufd得到测试函数的边界值、中点误差和不确定性误差，计算结果列于表1。

表1 利用不同方法得到的测试函数区间结果

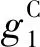
由表1的计算结果可以得出以下两点结论。

1)相比于IFE-first，由IFE-second得到的区间值更接近精确解，中点误差也更小，因此，一阶线性逼近对于非线性函数且带有大范围区间变量的结构的计算精度较差。此外，IFE-second和IFE-first的不确定性误差相同，表明这两种方法的区间值半径相同。

2)相比于IFE-first和IFE-second，显然，由IFE-ufd得到的边界值与精确解基本一致，尤其是IFE-ufd的中点误差为0.00。另外，考虑到利用IFE-second求解区间值的过程中，需要求取区间函数对区间参数的偏导数，而文中方法仅需线性地代入区间变量的中点和端点值就可得到区间函数的边界值，因此对实际工程具有更好的适用性。

为了测试IFE-ufd对不同变化范围的区间参数的稳定性，令λ由0.0变化到0.6，并利用上述4种方法求解测试函数的区间值，结果见图2。

从图2可以看出：当区间范围由小变大时，IFE-second和IFE-first与精确解之间存在明显偏差，尤其当λ为0.6时，这两种方法基本失效；而随着λ的增大，文中方法一直保持着较高的计算精度，曲线变化趋势与精确解几近相同。

同一图例符号对应的两条曲线分别表示相应区间方法的上界和下界

5 算例

图3为十杆桁架的示意图。桁架结构参数为：杆①-⑥长度L=3.6 m，截面积A①-⑥=0.03 m2，杆⑦-⑩截面积A⑦-⑩=0.02 m2。边界条件为：节点5和6为固定端，节点4受垂直作用力P1，节点2受垂直作用力P2和水平作用力P3。材料为Q235-A，

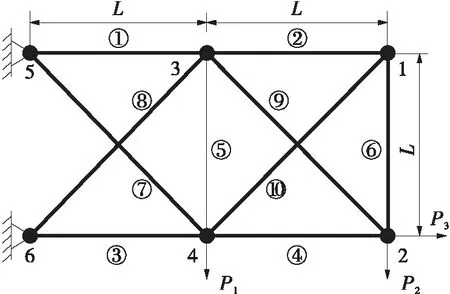
图3 十杆桁架示意图

相应的弹性模量以E表示。由于材料误差和载荷不确定性，P1、P2、P3和E被视作区间参数。表2中列出了各区间参数的信息。

表2 十杆桁架的区间参数信息1)

依据上述给定的条件，利用文中方法、IFE-second和IFE-first分别计算十杆桁架中节点2的垂向位移区间。文中方法的计算步骤如下：首先利用式(28)将十杆桁架位移函数分解为4个一维函数；由于分解后得到的一维函数仍然是隐式函数，因此调用十杆桁架的有限元程序求解各个区间变量的端点，以及区间变量中点处节点2的垂向位移；将得到的垂向位移代入式(30)，获得十杆桁架节点2的位移区间。

表3列出了不确定度λP和λE为0.2时节点2的静态位移区间、中点误差和不确定性误差。需要注意的是，IFE-first和IFE-second在求解响应函数对区间变量的偏导数时，对于数值算例可以直接求得，对于工程算例则需得到载荷阵和刚度阵，然后利用式(12)和(18)分别得到一阶和二阶偏导数。

表3 λP和λE为0.2时桁架节点2的位移区间

从表3可看出，与IFE-first相比，IFE-second和IFE-ufd的位移区间与精确解更为接近，但是由IFE-ufd计算得到的中点误差和不确定性误差比IFE-second的更小。再考虑到IFE-ufd因不需要求取桁架响应函数对区间参数灵敏度和刚度阵的逆而拥有更少的耗时，可以得出结论：文中方法具有准确性和适用性。

图4给出了当相对不确定度λP和λE变化时，利用IFE-ufd和Exact分别计算得到的桁架节点2的位移区间曲面。

图4 λP和λE对桁架节点2位移区间的影响

从图4可以看出：随着λP和λE的增大，桁架位移区间也在不断增大；同时，IFE-ufd与精确解的变化曲面非常接近。表明在整个不确定域内，文中方法均具有较好的计算稳定性。

6 结论

文中提出了一种单变量函数分解的区间有限元法，用于求解含区间参数的结构响应问题。与一阶和二阶区间摄动有限元法相比，单变量分解表达式包含了Taylor展开式中所有高阶单变量项，因此没有限制响应函数的非线性。在响应函数单调时，仅需计算变量端点和中点处的响应值，就可以得到响应的上、下界，方法简便、实操性强且无需求解响应函数的灵敏度和刚度阵的逆。数值算例结果表明，文中方法对具有强非线性且大范围变动的区间函数具有较快的计算速度和较高的计算精度。