高速铁路车-轨-桥耦合系统实时混合试验的高效计算方法

古泉 张德宇 国巍 武际亮 袁彬 周惠蒙 王涛

(1.厦门大学 建筑与土木工程学院，福建 厦门 361005；2.中南大学 土木工程学院，湖南 长沙 410075；3.中国地震局工程力学研究所 地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080)

实时混合试验是在拟动力试验的基础上发展而来的一种试验方法，又称实时子结构拟动力试验[1]。与拟动力试验相同，实时混合试验把试验对象分为两部分，将结构中难以进行准确数值模拟的部分作为试验子结构，其他具有明确力学特性的部分作为数值子结构[2- 4]。对于实时混合试验中数值子结构的计算，国内外学者提出了许多积分算法来提高积分的速度、准确性和稳定性，例如Newmark族积分算法[5]、CR[6]和KR-α[7]积分算法。而对于试验中出现的时滞问题，学者们也提出了许多经典的时滞补偿方法[8- 11]。在高速铁路系统的实时混合试验中，可以将列车作为试验子结构用振动台加载，桥梁作为数值子结构用有限元计算。但由于列车的运行速度往往很快，可以达到350 km/h，轨道梁的数值模型必须足够长，且列车试验子结构的控制要求精确的计算，必须采用足够精细化的车和桥梁模型，这就导致模型规模非常大，计算极其耗时[12]；同时，实时混合试验要求实时性，每一步都需要在极短时间内完成，对数值计算速度的要求很高[13]。因此，已有的积分算法方法不能满足高速铁路系统实时混合试验对计算速度和精度的要求。为解决这一难题，文中提出一种高速铁路车-轨-桥耦合系统实时混合试验的高效计算方法——移动荷载积分法。在进行实时混合试验之前将桥梁数值子结构计算所需要的数据进行存储，在实际计算时只需要将每一时步对应的数据进行抽取和计算，即可得到当前时步桥梁数值子结构的位移响应，从而可以在保证计算精度的同时获得较高的计算效率。

1 实时混合试验的移动荷载积分法

1.1 基于线弹性系统的移动荷载积分法

对于线弹性桥梁系统，随时间连续移动的轮轨作用力可以按照以下方式叠加，作用于桥梁结构上：

(1)

式中：x为桥梁位置；t为时间；n为计算的总时间步数；下标k为计算时步；tk表示第k时间步，xk表示当前时刻轮轨力的作用位置，对于以速度v运行的列车，tk与xk的关系为xk=vtk；F(xk，tk)为tk时刻作用于桥梁xk位置处的轮轨作用力，由混合试验测得；Lk(x，t)为tk时刻作用于桥梁xk位置处的三角形单位脉冲函数。f(x，t)与Lk(x，t)的函数图像如图1所示。

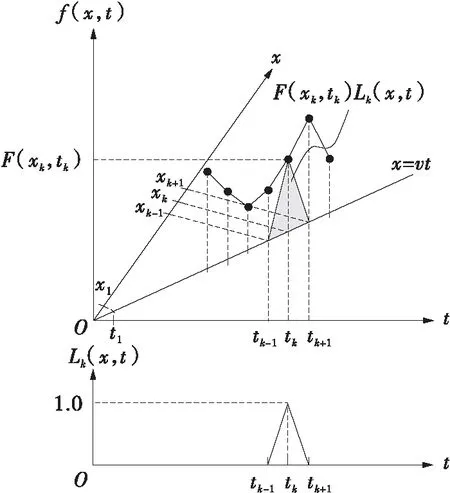
图1 f(x，t)与Lk(x，t)的函数图像

在线弹性结构中，桥梁在任意(x，t)处的位移可根据线性叠加原理计算：

(2)

式中：uk(x，t)为三角形单位脉冲Lk(x，t)所引起的位移响应，是位置x与时间t的二元函数，当k=1时，其函数图像如图2所示；u(x，t)也是位置x与时间t的二元函数，其函数图像如图3所示。

由式(2)可知，u(x，t)的叠加计算需要先计

图2 uk=1(x，t)的函数图像

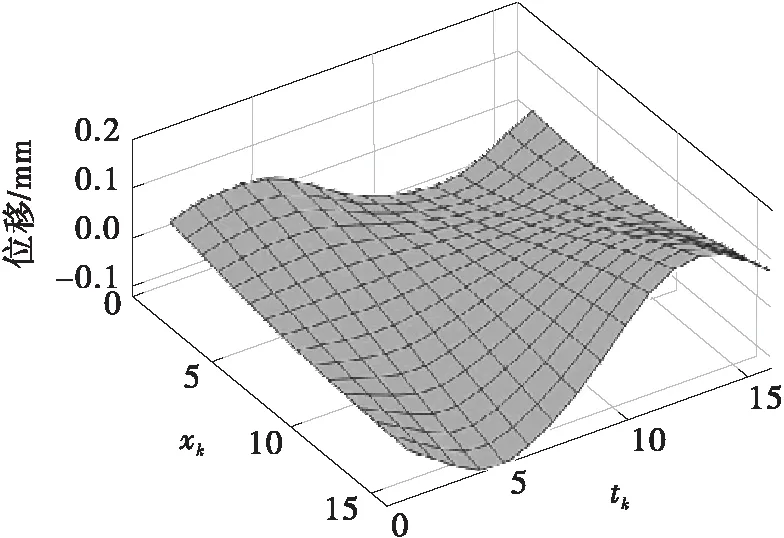
图3 u(x，t)的函数图像

算出uk(x，t)并进行存储，计算时再进行读取和叠加，所需要的总数据量是由计算的总时间步数决定的。在高速铁路车-轨-桥耦合系统的实时混合试验中，桥梁模型具有较大的总长度且时间步长极小，由式(2)计算u(x，t)的过程中需要存储和输入极大的数据量，每一步的计算耗时过长，无法满足实时混合试验的控制要求。

车桥实时混合试验模拟桥上行车的过程，在确定的车速以及时间步长下，每一时刻对应的桥上的轮轨作用力位置都是唯一的。由于在实时混合试验中每一时间步仅需要计算当前时刻轮轨作用力作用位置处的桥梁响应，而不需要计算桥梁的完整响应，因此对于各个时刻作用于对应位置上的单位脉冲来说，无需存储完整的结构反应函数，只需要存储单位脉冲作用时间后各时刻轮轨力在桥梁作用点处的位移响应。从大量数据中抽取这些特定点的数据，只存储最少的有效数据(如图4所示)，并在此基础上进行叠加计算，其他数据即为无效数据。

对于线性系统，在i时刻轮轨力作用位置处施加单位脉冲力，在j时刻对应位置处产生的位移响应记为uij(t)。对于动力分析来说，uij为一个矩阵，整个结构储存位移响应的数据结构如式(3)所示。

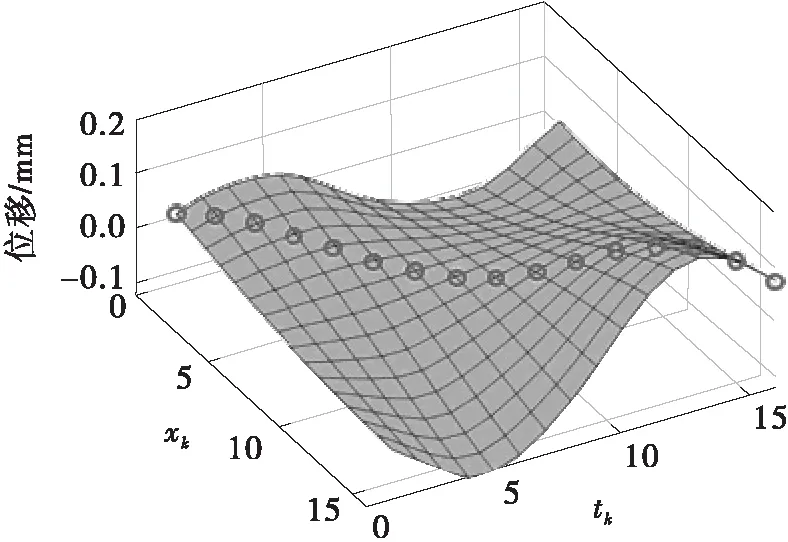
图中圆点表示有效数据点

在同时存在多个移动荷载的情况下，每个荷载分别采用这个数据结构，最终计算时对所有的数据进行线性叠加。在进行叠加计算时，只需要提取当前时刻之前作用的单位脉冲的响应数据中对应当前时刻的那部分进行叠加，而不需要对所有存储的响应数据进行叠加，可极大提高计算效率。

(3)

以i时刻为例，使用优化后的数据存储矩阵，特定时刻桥梁特定位置处的位移响应的计算过程为

(4)

式中，fn为tn时刻作用于桥梁对应位置处的真实轮轨作用力，即混合试验中所测得的实时轮轨力的大小。

由式(4)可知，为了计算每一时步轮轨力作用位置处的位移，从单位移动脉冲荷载作用下记录的整体响应中提取所需要位置的响应，形成数据矩阵，计算时仅需要提取对应数据进行线性叠加。因此，对于n时刻的响应计算，文中算法只需对n个数据进行叠加，极大地提升了计算速度。

由上文可知，移动荷载积分法要求在计算前事先存储好并在计算过程中实时读取一个维度为n×n的数据矩阵(n为计算的总时间步数)。即使这样，在实时混合试验中n的取值也可能比较大，因此这一过程会耗时较多。而事实上轮轨力的影响范围有限，足够远处(比如桥梁3～5跨以外)的影响可忽略不计，因此在实际计算中，矩阵U的列数n取有限值。考虑到移动荷载的有效影响范围确定，而行数会一直增加直到桥梁最末端，值得说明的是，该方法适用于桥梁跨度较小的连续梁桥或简支梁桥的情况，对于大跨度桥梁并不适用。在混合试验中，可以分批次读取数据矩阵，每次读入适当行(比如n行)，减少计算过程中单次读取的数据量，从而减少内存占用量并提高计算效率。

上述算法是基于线弹性系统和位移叠加法进行的，下面基于弹塑性数值子结构方法[14- 15]将移动荷载积分法拓展到局部非线性系统。

1.2 基于弹塑性数值子结构的移动荷载积分法

对于桥梁局部某些桥墩处可能出现非线性的情况，基于弹塑性数值子结构方法，桥梁整体仍采用最初的线性模型进行分析，而非线性区域构件则被隔离出来采用非线性模型计算[14]。计算线性和非线性构件的内力差值，将其作为非线性修正力加到桥梁节点上，非线性修正力作为外加荷载所引起的位移叠加在线性桥梁位移上，得出真实的非线性桥梁的位移响应，相当于在移动荷载引起的桥梁响应基础上再叠加一个非移动的荷载导致的响应。值得说明的是，非线性修正力引起的位移响应也可作为移动荷载叠加法的特例，基于式(4)计算得到，只是式(3)中矩阵取法不同，需保持荷载位置不变。

下面简单介绍数值子结构方法中非线性修正力的计算方法。

基于有限元的整体结构运动方程为

(5)

将式(5)按Newmark-β法对时间t进行离散:

(6)

式中，α、β为引入参数，Fn+1为等效外荷载。

在式(6)的左右两边同时加上Kun+1项并整理得

(7)

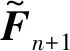
(8)

文中将非线性材料的本构关系直接编写进程序中，计算非线性构件的内力，并使用式(8)得到非线性修正力。

2 实时混合试验中的移动荷载积分法验证

文中试验的数值子结构模型采用如图5所示的轨道-桥梁系统，总长度为330 m，共11跨，轨道与桥梁的参数取值见表1。

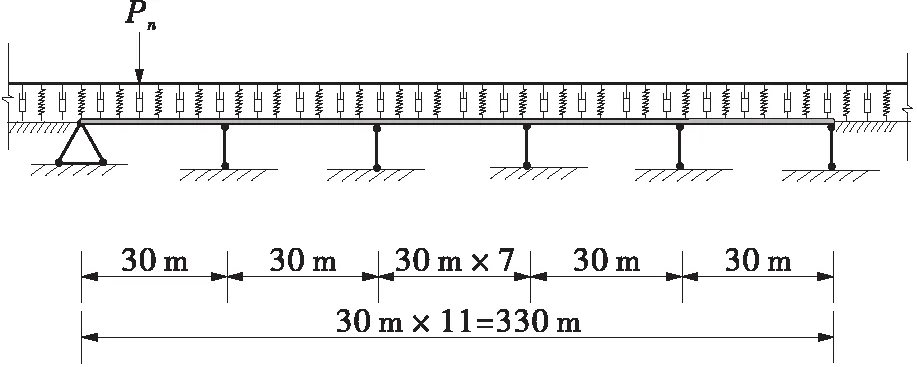
图5 轨道-桥梁系统

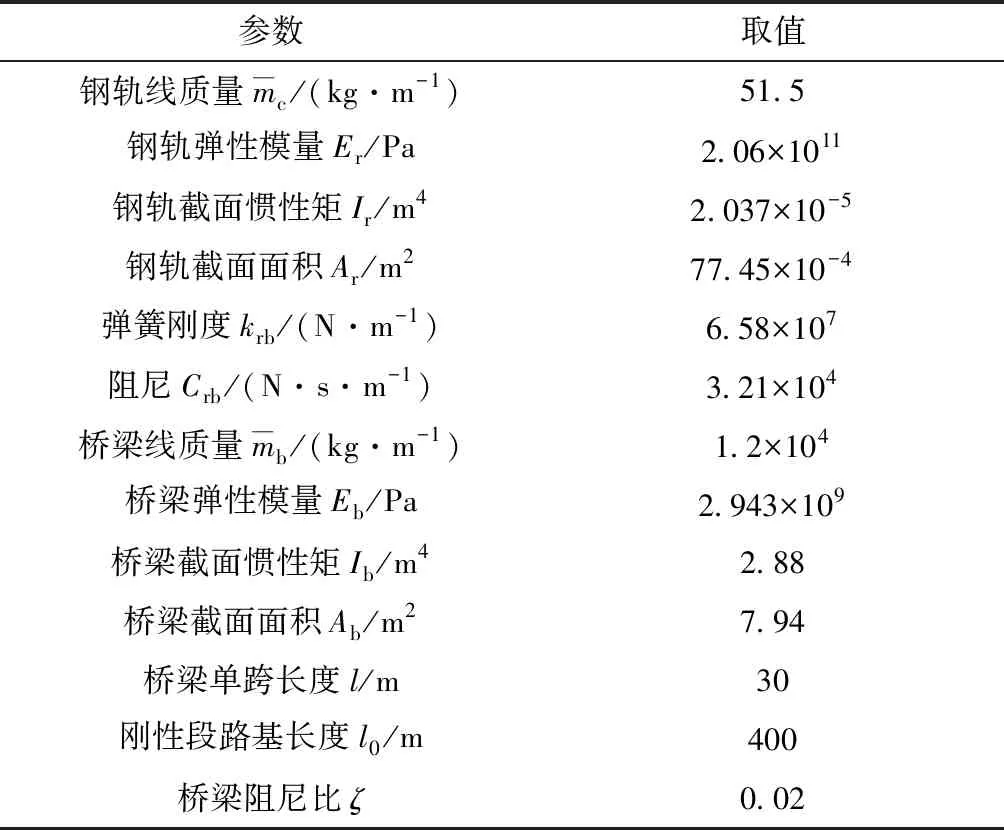
表1 轨道-桥梁系统的参数表

试验中采用如图6(a)所示的振动台系统，该振动台为电液式振动台，台面尺寸为1 m×1 m，可承载的最大荷载质量为10 t，可加载的有效频率为0.1～50.0 Hz，最大输出加速度为1.2g。选取四分之一CRH380A高铁机车车体(1个轮对)作为试验子结构。试验的时间步长为1/128 s，行车速度为230 km/h。为简化研究问题，对列车1个转向架中的1个轮对单独划分进行研究，如图6(b)所示。试验子结构的各项参数见表2。

(a)振动台系统

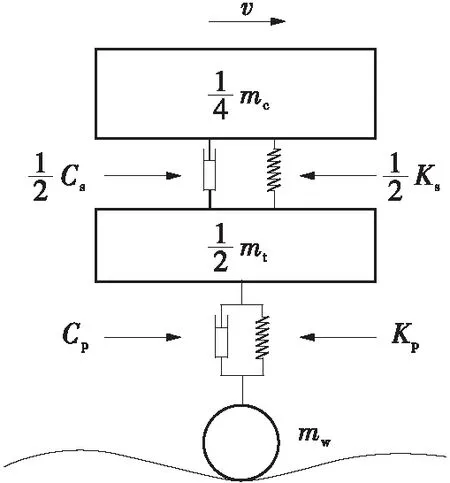
(b)简化后的四分之一车体模型

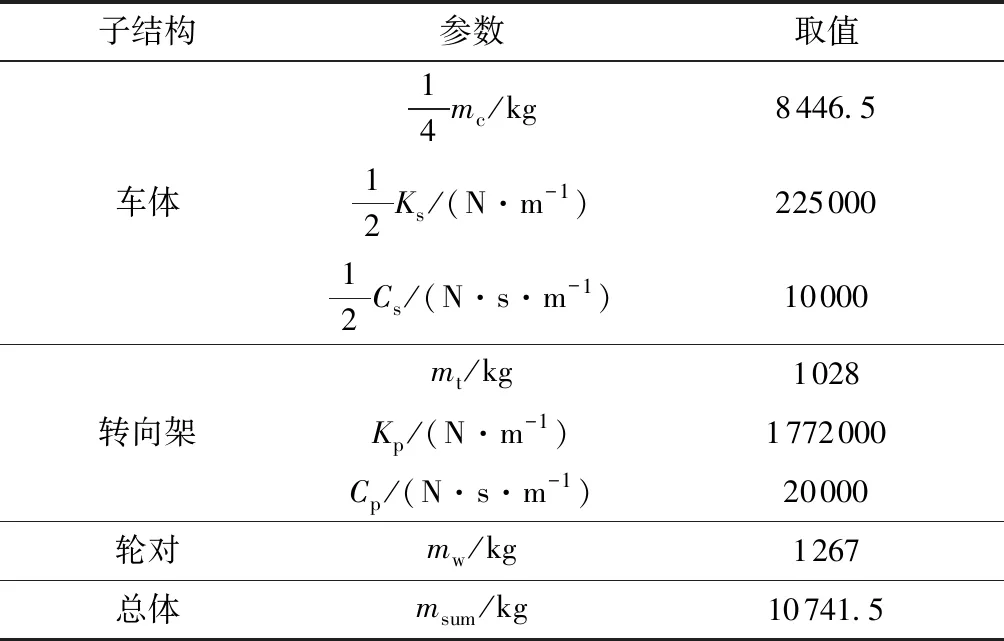
表2 试验子结构的参数1)

1)表中，mc、mt、mw分别为车体、转向架和轮对的质量，Ks、Kp分别为车体与转向架、转向架与轮对之间的弹簧刚度，Cs、Cp分别为车体与转向架、转向架与轮对之间的阻尼，msum为总质量(含轮对)。

在实时混合试验中，将轨道-桥梁系统作为数值子结构，通过移动荷载积分法计算出当前时步的位移响应，车体作为试验子结构，通过振动台加载并根据设备上的传感器实际测得的加速度计算出当前时步下的轮轨作用力。采用自适应时间序列(Adaptive Time Series)的时滞补偿方法[16](简称ATS方法)以减小桥梁数值子结构计算得出的位移命令信号与车辆子结构接收的输入信号之间的幅值及相位误差。

文中的实时混合试验使用Pulsar迭代控制方法(ICS)来进行系统响应的复现，通过Matlab/Simulink平台实现实时仿真，利用Simulink Real-time实时系统工具箱将Simulink编译的模型运行在另一台目标主机(xPC-Target)上，Simulink Real-time支持SCRAMNet接口，使用SCRAMNet将Pulsar系统中的各类信号实时向外发送，同时将外部的控制指令读入Pulsar。

2.1 线弹性系统下的移动荷载积分法验证

本节验证移动荷载积分法应用于实时混合试验中的线弹性系统的可行性与效果。在应用移动荷载积分法进行计算前，需要先计算出车辆行驶前自重荷载所引起的轨道-桥梁系统的初始位移，并将单位脉冲荷载按照实际计算时的时间步依次加载到轨道-桥梁模型上的相应位置，记录当前加载情况下桥轨所有节点的全时程位移响应。根据所记录的全部加载情况对应的位移响应，选取其中单位脉冲作用时间之后各时刻轮轨力在桥梁作用点处的位移响应，即图4中的有效数据点，形成式(3)中的移动荷载积分法的基本数据矩阵。然后根据式(4)即可计算得到每一时步下轨道-桥梁系统的位移响应。

试验流程如图7所示。将第i步移动荷载积分法计算出的位移加载到试验子结构上，通过振动台测出的加速度计算出第i+1步的轮轨力，将其加载到数值子结构，再计算出第i+1步的位移，将其加载到试验子结构上，不断重复这个过程直至试验完成。

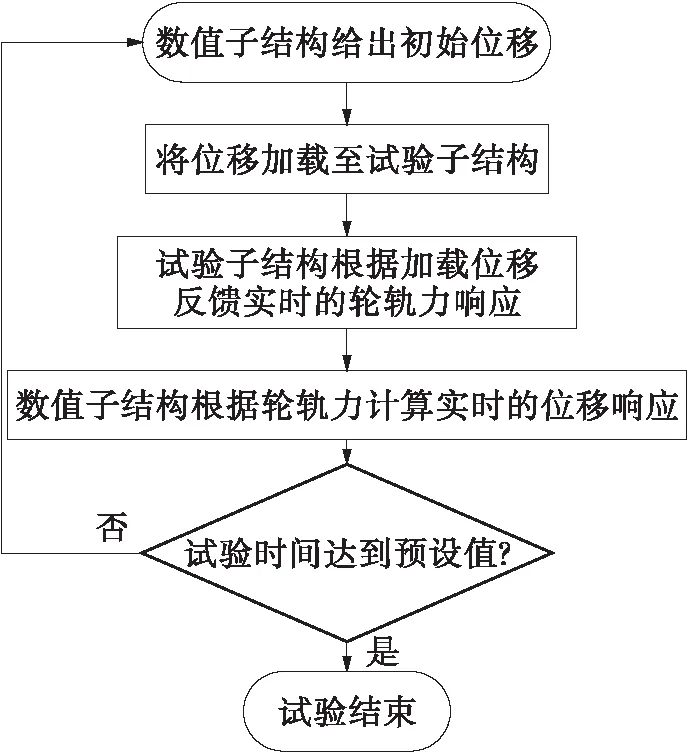
图7 线弹性系统下的实时混合试验流程

图8是试验过程中轮轨力随时间变化的情况。在OpenSees中建立与试验相同的轨道-桥梁数值模型，将试验过程中记录下的轮轨力按对应时间步进行加载，对比数值求解的结果与试验子结构记录的命令信号，如图9所示。使用ATS方法进行时滞补偿后，本次试验的平均时滞为9.9 ms。将试验中的命令信号时滞处理后，与数值解进行对比，结果如图10所示。所得结果验证了移动荷载积分法应用于线弹性系统下的实时混合试验的可靠性。

图8 线弹性系统下的试验轮轨力

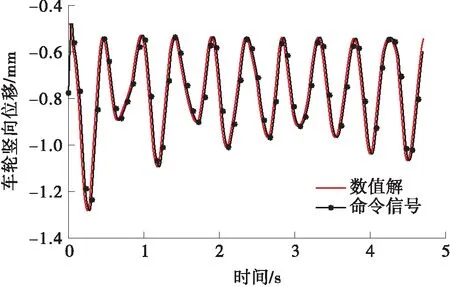
图9 线弹性系统下数值信号与命令信号的对比

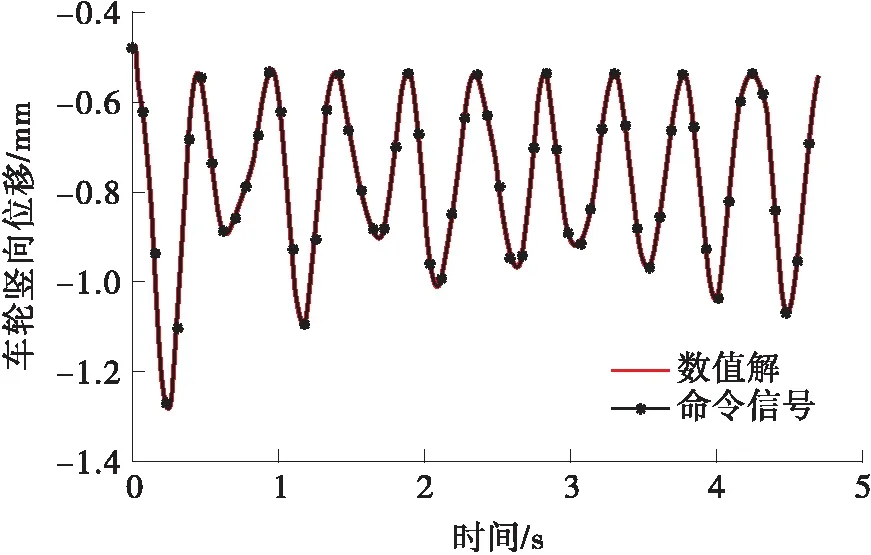
图10 线弹性系统下消除时滞后数值信号与命令信号的对比

2.2 非线性系统下的移动荷载积分法验证

本节验证基于弹塑性子结构方法的移动荷载积分法应用于实时混合试验中的非线性系统时的可行性。在2.1节算例的基础上将跨中处的支座替换为非线性支座来模拟桥梁局部非线性问题。非线性支座采用Duffing材料，材料本构关系如下：

σ=E(ε+γε3)

(9)

式中，E=13.89 MPa，γ=-3 000，σ、ε分别为应力和应变。

与2.1节相同，选取四分之一CRH380A高铁车体机车(1个轮对)作为试验子结构，试验的时间步长为1/128 s，行车速度为230 km/h。

该算法应用于非线性系统时的计算过程比较复杂，下面结合算例作具体介绍。首先将本算例中的非线性结构用2.1节算例中的线性结构来代替，此时整个桥轨系统均为线弹性(即转化为线弹性问题)，将单位荷载按照时间步依次作用于轨道-桥梁模型上的相应位置，记录当前加载情况下桥轨所有节点的全时程位移响应。根据记录的全部加载情况对应的位移响应，形成移动荷载积分法的基本数据矩阵。考虑非线性系统与线性系统之间的内力区别，在基本数据矩阵之外，需要编制其他两类数据矩阵。第1类矩阵(矩阵A)是单位荷载在当前时步作用下非线性节点处的位移响应。本算例中的非线性支座的两端均为非线性节点，故需要记录单位荷载按照时间步依次作用于轨道-桥梁模型上相应位置时两个节点的全时程位移响应。根据记录的非线性节点的位移响应，形成对应的数据矩阵，用于后续计算非线性修正力。第2类矩阵(矩阵B)是单位荷载作用于非线性节点时轨道-桥梁模型各节点的位移响应。在本算例中，将单位荷载按照时间步依次作用于非线性节点上，记录下当前加载情况下轨道-桥梁模型各节点的全时程位移响应，然后形成对应的数据矩阵。

在编制完所需的数据矩阵进行实际计算时，先根据移动荷载积分法的基本矩阵计算出线性情况下当前时步对应位置处的位移响应，再根据矩阵A计算出当前时步下非线性节点处的位移，使用该位移并结合程序中非线性材料的本构关系公式计算当前时步下非线性节点处的非线性修正力，根据矩阵B计算出非线性修正力作用于非线性节点时荷载作用位置处的位移响应，叠加之前得到的线性情况下的位移响应，最终得到结构真实的位移响应。

具体的实时混合试验流程如图11所示。将第i步移动荷载积分法计算出的位移加载到试验子结构上，通过振动台测出的加速度计算出第i+1步的轮轨力，将其加载到数值子结构。数值子结构首先根据轮轨力计算出线弹性系统下当前时步轮轨力作用位置处的位移响应，然后计算出当前时步的非线性修正力，由非线性修正力对线弹性系统下的位移响应进行修正，最终计算出第i+1步的位移，将其加载到试验子结构上，不断重复这个过程直至试验完成。

图11 非线性系统下的实时混合试验流程

图12是非线性系统下试验过程中轮轨力随时间变化的情况。同样将试验过程中记录下的轮轨力按对应时间步加载到OpenSees中的数值模型进行计算，对比数值求解的结果与试验子结构记录的命令信号，如图13所示。使用ATS方法进行时滞补偿后，本次试验的平均时滞为8.6 ms，将命令信号根据试验时滞处理后，与数值解进行对比，结果如图14所示。所得结果验证了基于弹塑性数值子结构的移动荷载积分法应用于非线性系统下的实时混合试验的可靠性。

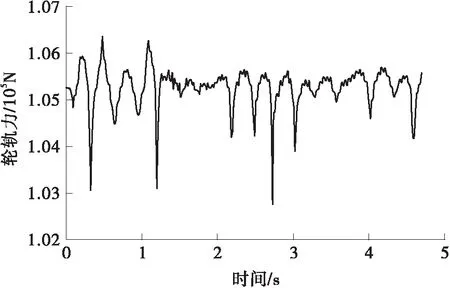
图12 非线性系统下的试验轮轨力

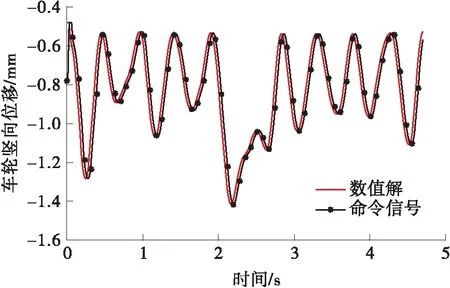
图13 非线性系统下数值信号与命令信号的对比

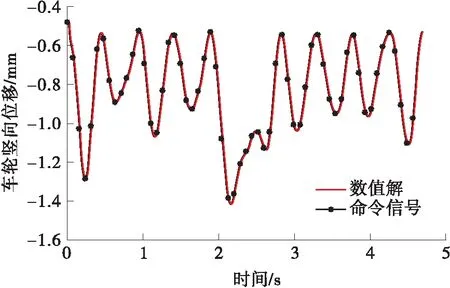
图14 非线性系统下消除时滞后数值信号与命令信号的对比

3 结语

为高效、精确地进行高速铁路车-轨-桥耦合系统实时混合试验的计算和模拟，提出了一种新型计算方法——移动荷载积分法，并得到如下结论。

1)将移动荷载积分法应用于实际的高速铁路系统实时混合试验中，试验中每一时步的操作(数值计算、数据交换、时滞补偿和作动器加载等环节)均可在1/128 s内完成，满足实时混合试验对于计算速度的要求。需要注意的是移动荷载积分法仅适用于线弹性桥梁结构；当出现局部非线性时，结合弹塑性数值子结构方法可以较好地解决。

2)将消除时滞后数值求解的结果与试验子结构记录的命令信号进行对比，发现试验结果拥有可靠的精度——在线弹性系统下，误差为1×10-10量级；在非线性系统下，误差为1×10-5量级。

文中选取四分之一CRH380A高铁机车车体(1个轮对)作为试验子结构，未考虑轮对间的动力叠加效应，在实际应用中，应考虑其影响。