大时滞系统中Smith控制算法改进与应用
2021-04-08曹学海邱国鹏卢文杰
曹学海,于 敏,邱国鹏,卢文杰
(三明学院,福建 三明 365000)
在实际生产应用中,由于工况复杂,外界因素多变等原因,大部分控制系统存在时滞现象。面对时滞系统闭环特征方程具有时滞项的问题,传统PID控制不能立刻产生抑制作用[1-2]。针对系统时滞问题,史密斯提出了Smith预估控制方案,通过预估系统的动态特性并进行补偿,减少超调量和加速调节过程[3]。由于该方案是基于精确数学模型而设计的,对模型参数变化适应能力差,而实际生产过程中,往往无法获得精确的数学模型,在一定程度上限制Smith预估控制器的应用范围。在PID控制算法优化研究方面,文献[4]用模糊控制器作为系统控制器,利用模糊控制良好的鲁棒性,提高控制系统的性能。虽然模糊控制无需精确的数学模型,抗干扰能力强,鲁棒性良好,但是它主要依靠操作人员的工作经验和直观判断,导致模糊控制的精度不高。为了提高系统控制的精度,将PID控制器与模糊控制相结合的模糊PID复合控制器在实际生产中得到应用[5]。然而在具有滞后特性的控制系统中,模糊PID复合控制算法在模糊切换时控制系统的稳定性无法得到保障[6-7]。文献[8]将模糊PID自适应控制器当作系统控制器,在线自适应调整系统参数,改善了模糊切换导致的不稳定状况,但是一旦模型失配,仍然难以取得理想的控制效果。与此同时,Smith预估器的优化研究也在不断地进行,文献[9]将Smith预估控制与神经网络相结合构造了一种补偿Smith-RBF神经网络控制策略,利用RBF神经网络进行实时参数调整,增强了系统的抗干扰能力。文献[10]将自适应思想与Smith预估器相结合,实现大时延和环境参数未知情况下的有效控制。文献[11]对Smith预估模型参数实现了多目标优化,有效地克服了系统的非线性。
本文针对实际生成过程中常规PID-Smith控制器在滞后时间多变的环境下存在着超调量大、稳定性弱等缺点,提出一种改进型模糊自适应Smith预估控制器,实验结果表明该方案在一定程度上减少了被控对象因系统时间滞后带来负面影响。
1 常规Smith预估控制器
针对滞后系统中闭环特征方程含有纯滞后项的问题,史密斯提出一种预估补偿控制的方法,在反馈控制基础上,引入一个预估补偿环节,使闭环特征方程不含纯滞后项。通过预估被控模型的动态特征,利用预估模型进行时滞补偿,形成一个没有时间滞后的被控模型,具体结构如图1所示。

图1 常规Smith预估器的基本结构
图中Gm(s)为预估模型无滞后的部分,exp(-Lms)为预估模型纯滞后的部分,两者的结合Gm(s)exp(-Lms)为Smith预估模型的传递函数,Gp(s)exp(-Ls)为实际被控模型的传递函数,系统控制器Gc(s)为PID控制器。当模型精确时,即Gm(s)=Gc(s),Lm=L,得到的闭环系统传递函数为:
(1)
其特征方程为
1+Gc(s)Gp(s)=0
(2)
从(2)式中可看出,在实际被控对象与预估模型完全一致的前提下,通过Smith预估补偿作用,闭环系统的特征方程式中的纯滞后项被消除了,只是它的输出滞后了一个L的时间。但是在绝大部分具有滞后特性的控制系统中,实际被控模型的参数通常受到外界影响,具有时变性、不确定性。当实际被控对象与预估模型有误差时,则有
(3)
由(3)式可知,实际被控对象和预估模型的误差越大,即Gp(s)与Gm(s)以及L与Lm相差越大,补偿效果就越差。因为纯滞后为指数形式,所以纯滞后的误差比Gm(s)的误差影响大,即Lm的精度更关键。
2 改进型预估控制算法的设计
2.1 模糊自适应PID控制
模糊自适应PID控制的系统结构主要是由PID控制调节器和模糊推理机两部分构成,其具体结构如图2所示。模糊自适应PID控制器以误差e以及误差的变化率ec作为模糊控制器的输入信号,PID控制器的参数kp、ki、kd作为输出信号。模糊控制规则的作用下对PID控制器参数实时修正,满足不同时刻的e以及ec对PID参数自整定的需求。输出变量的值为kp、ki、kd的原始值分别加上控制参数的增量Δkp、Δki、Δkd,计算方法如下:
(4)
(5)
(6)

图2 模糊自适应PID控制器结构图
在模糊自适应PID控制器中,模糊推理机的输入变量为e和ec,Δkp、Δki、Δkd作为模糊推理机的输出。取e、ec、Δkp、Δki、Δkd的基本论域分别为[-10,10]、[-1,1]、[-3,3]、[-0.03,0.03]、[-0.03,0.03],并将误差e和误差的变化率ec以及输出量Δkp、Δki、Δkd的模糊子集均定义为{负大、负中、负小、零、正小、正中、正大},且简记为{NB、NM、NS、ZO、PS、PM、PB},同时量化到[-3,3]的区域内。由于三角形的隶属函数具有灵敏度高的优点,因此本文模糊自适应PID控制器中的输入输出变量均用三角形函数作为模糊子集的隶属度函数。根据实际控制经验,在具有时滞特性的控制系统中,在不同误差和误差变化率自动调整下,模糊自适应PID的控制参数的变化符合以下3条规律[14]:
①当误差e偏大时,取偏大的kp和偏小的kd,为了减小系统超调量,取ki=0;
②当误差e和误差的变化率ec处于中等大小时,取偏小的kp,取适中的ki和kd;
③当误差e偏小时,kp和ki取偏大值,kd取适中值,为了抑制系统大幅度振荡,误差的变化率ec偏小时,kd取偏大值;反之,kd取较小值。
根据以上规律建立模糊规则表,见表1-表3。

表1 Δkp的模糊规则表

表2 Δki的模糊规则表

表3 Δkd的模糊规则表
2.2 模糊自适应PID-Smith预估控制器
由于Smith预估器都是基于精确数学模型而设计的,对模型的变化敏感,滞后时间变化更关键。
本文提出一种改进型模糊自适应PID-Smith控制器,其基本结构如图3所示。

图3 改进型模糊自适应PID-Smith的基本结构
在图3中,R(s)为系统控制输入,Y(s)为系统控制输出,Gp(s)为实际被控模型的无时滞部分,exp(-Ls)为实际被控模型的纯时滞部分。Gm(s)为预估模型无时滞部分,exp(-Lms)为预估模型的纯时滞部分,一阶滤波器与Gm(s)的参数保持一致。改进型控制算法采用模糊自适应PID控制器作为系统控制器,并在常规Smith预估器时滞环节前引入了一个内反馈环和一个一阶滤波器,降低系统对滞后时间失配的敏感度。
3 仿真实验
生产过程中典型的滞后系统可以简化成一个滞后环节和一个惯性环节相串连的形式,其传递函数一般可描述为:
G(s)=K·exp(-Ls)/(Ts+1)
(7)
式中,K为对象模型的开环增益;T为时间常数;L为滞后时间;s为复变量。设定目标值为100,PID参数取kp=1.8、ki=0.05、kd=0.2。以被控对象G(s)=e-30s/(60s+1)。由于L/T=0.5,故可视为大滞后系统。当预估模型的滞后时间Lm=30保持不变,实际被控模型的滞后时间L分别为30、40、50、60时,并在1500~2000秒的时候施加25~30的动态干扰信号,将常规Smith预估方案与改进方案进行仿真对比实验,实验结果如图4-图7所示。

图4 被控模型滞后时间L为30的仿真对比图
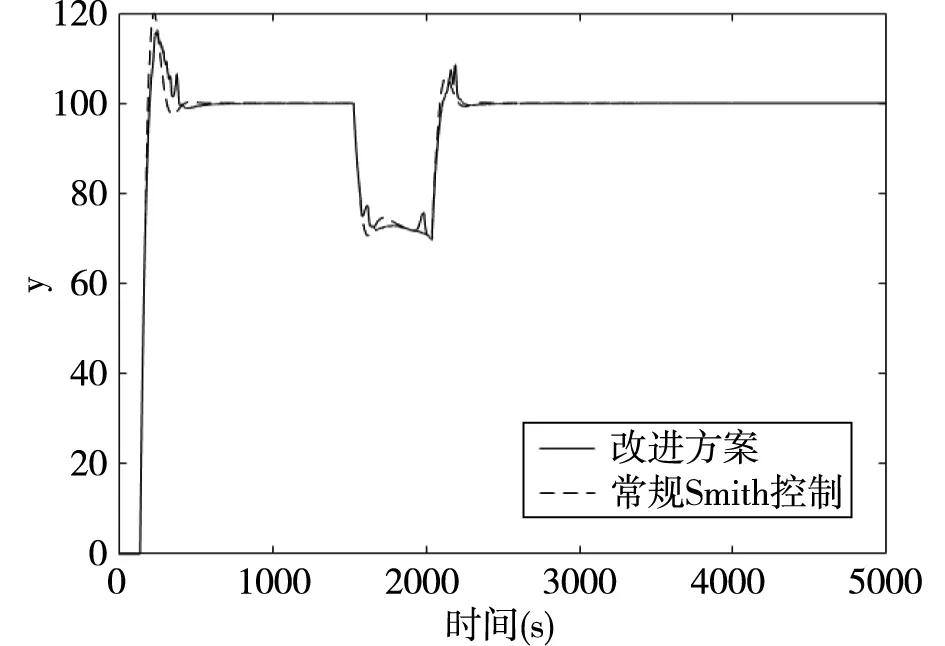
图5 被控模型滞后时间L为40的仿真对比图
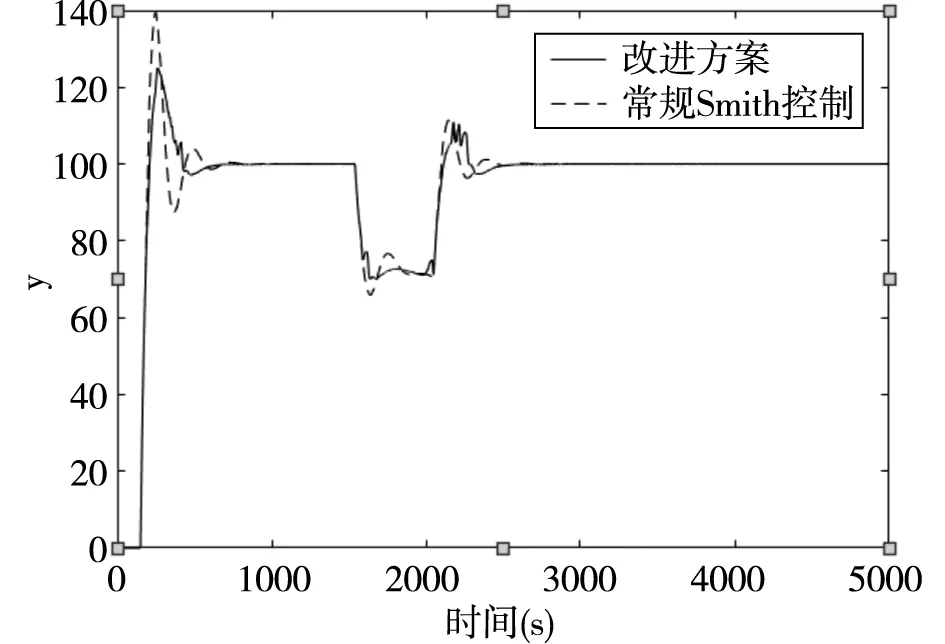
图6 被控模型滞后时间L为50的仿真对比图
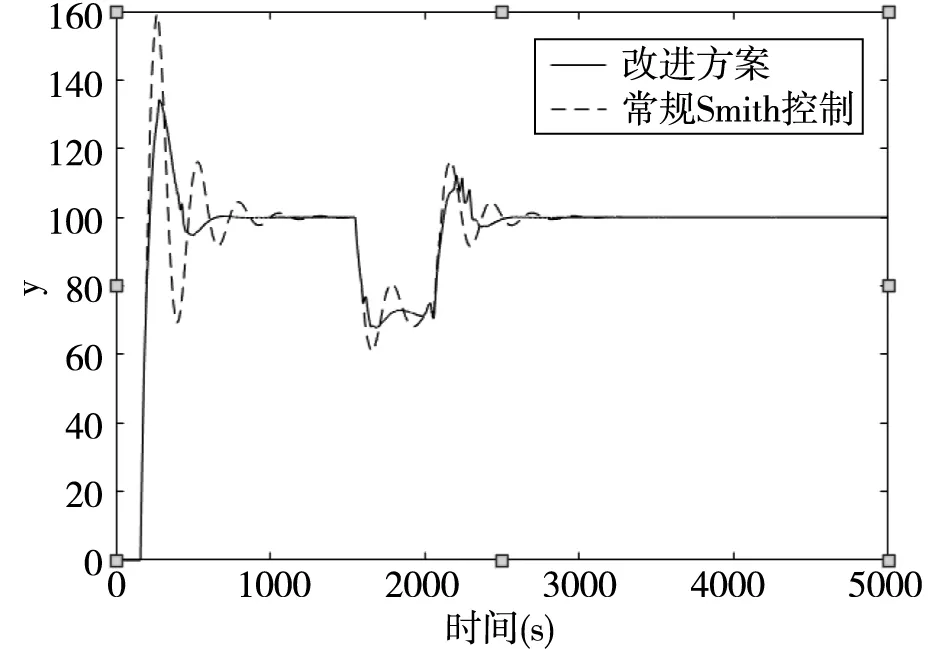
图7 被控模型滞后时间L为60的仿真对比图
通过对图4-图7的分析,得到的仿真实验结果如表4所示。
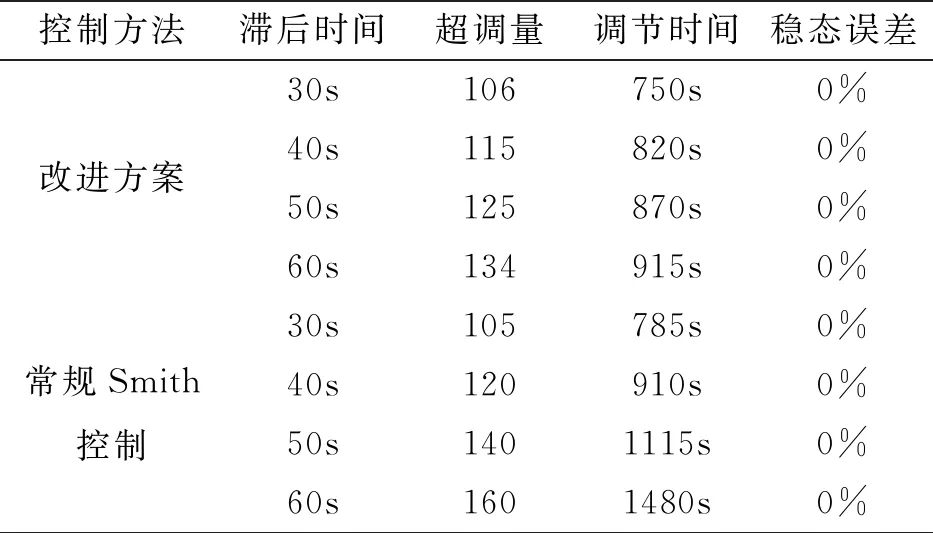
表4 仿真实验关键数据对比表
仿真对比实验表明:在模型精确的时候,即预估模型和被控模型的滞后时间均为30时,改进方案与常规Smith控制仿真曲线基本一致;随着被控模型的滞后时间增大为40、50、60时,改进方案受影响较小,在一定程度上减小了系统振荡范围,改善了系统超调量。
结语
本文在研究具有滞后特性的控制系统时,针对常规Smith预估控制器对精确模型的依赖性问题,结合自适应控制和模糊控制理论,提出一种新型的模糊自适应PID-Smith预估控制方案。仿真结果表明:在滞后时间波动的情况下,该方案在一定程度上改善了滞后系统中控制不稳定和超调量大的问题,取得了良好的控制效果,具有一定的实用性。
