基于杂波扩展的STAP投散射干扰方法
2021-04-08张剑云周青松
王 坤,张剑云,周青松
(国防科技大学电子对抗学院,合肥,230037)
与地面雷达相比,机载预警(AEW)雷达系统在提供连续侦察和监视方面具有很大的优势。但机载雷达波束对地面的下俯角较大,使得雷达接收到的杂波功率很大。此外,运动引起的杂波谱多普勒展宽导致对低多普勒目标的可检测性下降。空时自适应处理(STAP)通过隐式平台运动补偿实现最优杂波抑制,在AEW雷达系统中得到了广泛应用[1-5]。在电子对抗领域,对STAP的干扰是一个越来越受关注的研究课题,薛冰心等人基于线性调频信号距离和多普勒频移的耦合关系研究了频移假目标干扰[6],秦兆锐等人研究了移频灵巧噪声干扰[7],沈佳琪等人研究了间歇采样转发干扰[8],赵燕慧等人研究了延时混叠转发干扰[9],李骥阳等人研究了基于间歇采样的卷积调制干扰[10-11],张嘉曦研究了延迟转发干扰[12],谌诗娃等人研究了投散射式伪杂波干扰[13-14],这些干扰方法均为相干干扰,需要对雷达信号进行截获和采样,其中投散射式伪杂波干扰明确了采用干扰机主瓣对准雷达主瓣的方式来截获雷达信号,而其它几种干扰方法并未说明。考虑到AEW雷达应用的超低副瓣技术,若干扰机作为单独平台,这几种干扰方法应该也是采用主瓣对主瓣的方式来截获雷达信号,这使得干扰机本身被雷达发现的概率大增。根据干扰路径的不同,这些干扰可以分为直接路径干扰和多路径干扰。频移假目标干扰、间歇采样转发干扰、延迟转发干扰都是直接路径干扰,干扰波束需要指向雷达。投散射式伪杂波干扰则是一种多路径干扰,干扰机主瓣对准地面,利用地物散射特性和雷达、干扰机、地面运动特性产生类似杂波的干扰信号,通过地面散射进入雷达主瓣以达到干扰效果,当干扰机本身在雷达主瓣内时,这种干扰方法功率利用效率不如直接路径干扰。
本文结合两类干扰方法的优点,提出一种基于杂波扩展的STAP投散射干扰方法,干扰机本身不在雷达主瓣内,降低了自身被发现的概率,不对雷达直达信号进行截取和采样,而是对雷达信号经地面散射的杂波信号进行截取和采样,由于杂波相当于地面环境对原雷达信号进行调制,保证了与原信号的相干性,经采样、调制、延时转发给雷达后能获得相干增益,利于达到干扰效果。采用投散射的方式,通过选择合适的投射位置使干扰信号经地面散射进入雷达主瓣,使不在雷达主瓣内的干扰机能对雷达进行主瓣干扰。
1 功率计算
本节主要给出干扰机接收到的雷达直达波功率和雷达杂波功率计算公式。若杂波功率大于直达波功率,则说明对杂波信号而非直达波信号进行截取和采样具有可行性。
1.1 干扰机接收到的雷达直达波信号功率
机载预警雷达、干扰机和目标的空间配置见图1,雷达主瓣对准目标,干扰机不在雷达主瓣内。雷达A的飞行高度为HA,与干扰机J距离为RJ,相对于干扰机的方位角为φjr,俯仰角为θjr,发射功率为Prt,工作波长为λ,天线增益为Gr(φ,θ)。干扰机飞行高度为HJ,天线增益为Gr(φ,θ),相对于雷达的方位角为φrj,俯仰角为φrj,则根据基本雷达方程,干扰机接收到的雷达直达波功率为:
(1)

图1 雷达、干扰机、目标配置图
1.2 干扰机接收到的雷达杂波信号功率
干扰机除了接收到雷达直达波外,还能接收到经地面散射的雷达杂波信号。满足到雷达和干扰机的距离之和相等的散射点在空间中形成若干个椭球,它们与地面相交形成若干个椭圆,即干扰机接收到的雷达杂波等距离环。下面以距离之和为R的椭球为例,通过选择合适的坐标系,求出椭球与地面相交形成的杂波等距离环的解析表达式。

图2 雷达、干扰机几何配置图
如图2所示,以雷达地面投影点A′为原点,雷达、干扰机连线的地面投影为轴,AA′为轴,垂直AA′和JJ′所在平面作y′轴建立坐标系。以雷达和干扰机连线为轴,连线段中点为原点o,在AA′和JJ′所在平面内作轴垂线为轴,平行于y′轴作y轴建立坐标系,则在坐标系中椭球为标准椭球,其长轴为R,焦距为RJ,其方程为:
(2)
通过旋转和平移可以得到在坐标系中通过地面某散射点(xi,yi,0)的椭圆方程为:
(3)
通过将式(3)展开为二元二次方程的形式:
(4)
可以将椭圆的半长轴a、半短轴b分别表示为:
(5)
其中:
(6)

图3 杂波等距离环示意图
杂波等距离环如图3所示,内侧椭圆即为式(3)表示的椭圆,外侧的不规则形状则是由干扰机接收机分辨单元所形成的,这些分辨单元将整个杂波环分为m块,其中第i块杂波块P的面积即为图3中阴影部分所示,φji为P相对于干扰机投影点J′的方位角,φ1和φ2由干扰机波束宽度φjB决定,满足:
(7)
以J′为原点建立极坐标系,可以将椭圆方程改写为:
(8)
式中:rj为雷达干扰机地面投影距离;r(φ)为某杂波块到J′的距离;φ为其对J′的方位角,用l表示rj+B/2A,可将r(φ)表示为φ的函数形式:
(9)

由此,杂波块P的面积可以用积分表示为:

(10)
式中:Δ是干扰机接收机距离分辨单元在地面的投影,Δ=cτsecθji,c为光速,τ为雷达脉冲宽度,θji为P相对于干扰机的俯仰角。根据文献[15]中给出的表面杂波雷达方程,干扰机接收到杂波块P散射的功率为:
(11)
式中:φri、θri为P相对于雷达的方位角和俯仰角,φji为P相对于干扰机的方位角;σ0为散射系数;r1为P到雷达的距离;r2为P到干扰机的距离。干扰机接收到该杂波环的杂波总功率为:
(12)
2 信号模型
2.1 干扰机接收到的雷达直达波信号模型
机载预警雷达A、干扰机J和杂波块几何配置如图4所示,雷达以速度vA沿x轴方向飞行,干扰机以速度vJ飞行,飞行方向与x轴夹角为δj。
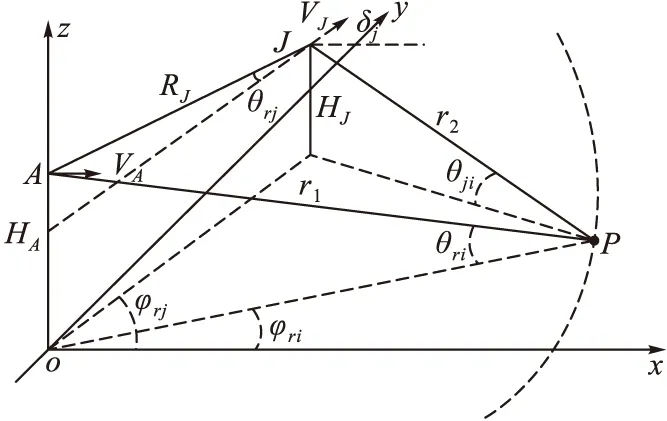
图4 雷达、干扰机、杂波块几何配置图
假设雷达发射信号为:
st(t)=Re[AtE(t)ejwct]
(13)
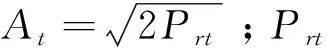
vr=vAcosθrjcosφrj-vJcosθrjcos(φrj-δj)
(14)
干扰机接收到的信号为Re[ArE(t-τ)ejωc(t-τ)],其中τ=(RJ-vrt)/c,由相对运动产生的多普勒频移为vr/λ。
2.2 干扰机接收到的雷达杂波信号模型
如图4所示,杂波块P到雷达、干扰机的距离之和R2w=r1+r2是随时间变化的,不妨设t=0时,R2w=R0。在t时刻,干扰机接收到的信号是雷达在t-τ(t)时刻发射的,此时有:
R2w(t-τ(t))=R0-(vAcosφricosθri+
vJcos(φrj-δj)cosθji)(t-τ(t))
(15)
可以解出:
τ(t)≈
(16)

(17)
根据文献[1],干扰机接收到的由杂波块P散射的信号为:
(18)

假设杂波回波可等效为NC个独立杂波块散射信号之和,由于各信号多普勒频移不同,各信号是相互独立的,干扰机接收到的总的杂波信号sjr(t)可以写为:
(19)
2.3 雷达接收到的干扰信号模型

(20)
式中:fj是干扰机对式(19)表示的接收信号进行调制处理得到的虚假多普勒频率。机载雷达的天线阵列布局如图5所示,为线性侧视阵列,则干扰机接收的单一散射块干扰信号的时间相位项和空间相位项分别为:
(21)
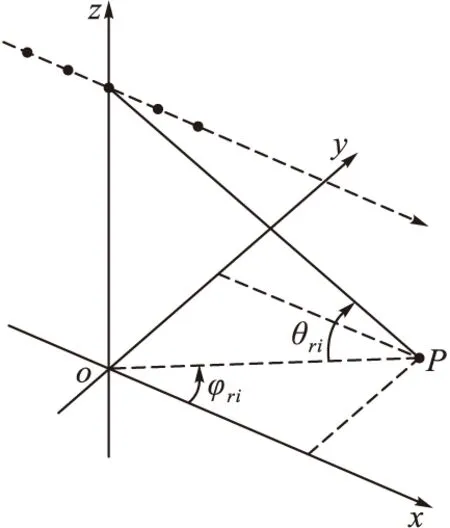
图5 雷达天线阵列布局
加上传感器方向图D(φ),阵列方向图G(φ,m),地面反射率L(φ),那么在第m个时刻第k个传感器接收到的一个距离单元总的干扰信号为:
jmk=
(22)
3 干扰基本原理
3.1 投散射式伪杂波干扰原理

(23)
fdj可以表示为方位角φri和虚假多普勒频率fj的函数:
fdj=F(φri,fj)
(24)
由于fdj的方位依存性,伪杂波干扰信号的功率谱与杂波功率谱类似,具有空时二维性,如图6所示,文献[14]中将其称为伪杂波。从图6(b)可以清楚地看到伪杂波谱占据了所有的方位,通过控制fj可以使伪杂波谱在空时平面上沿多普勒频率方向平移。


图6 伪杂波干扰下的功率谱(fj=450Hz)
与杂波相同,伪杂波在单一维度上是无法滤除的。STAP处理器像处理杂波一样处理伪杂波。伪杂波干扰前、后在40°方位角上的改善因子如图7所示,可以看到干扰后,不仅了产生一个杂波凹口以滤除杂波,还产生了一个伪杂波凹口以滤除伪杂波。其它方位角上的改善因子图与此类似。通过调整fj可以使伪杂波谱在空时二维平面上平移进而使伪杂波凹口沿多普勒频率方向平移,当目标的多普勒频率fdt和方位角φrt满足式(24),即fdt=F(φrt,fj)时,目标被伪杂波凹口覆盖,STAP处理器在滤除伪杂波的同时将目标也滤除了。

图7 伪杂波干扰前、后改善因子对比(φrt=40°)
由以上分析可知,要使伪杂波凹口准确覆盖目标需要知道目标的多普勒频率、方位角和所在距离单元等先验信息。这种对先验信息的高要求是投散射伪杂波干扰方法的最大短板。若干扰指标要求使目标处的响应下降10 dB以上,定义伪杂波凹口宽度D为改善因子-10 dB处对应的归一化多普勒频率范围,则由图7可知,当目标先验归一化多普勒频率误差超过D/2时,将不满足干扰指标要求。
与传统的转发式干扰形成具有不同多普勒频率或不同距离的假目标不同,投散射式伪杂波干扰利用STAP处理器特性将真实目标信息滤除,而传统转发式干扰下STAP能同时获取真实目标和假目标信息,且真实目标与假目标具有相同的方位信息。
3.2 基于杂波扩展的投散射干扰原理
由式(20)可知基于杂波扩展的投散射干扰相当于位于同一位置的NC部干扰机同时进行伪杂波干扰,干扰机的功率PJ需分配到这NC个干扰信号上,每个干扰信号的功率为PJ/NC。干扰后的功率谱如图8所示,可以看到干扰功率谱相当于将图6中的伪杂波谱压扁,将功率分配到更多空时位置上。


图8 基于杂波扩展的投散射干扰下的功率谱(fj=450Hz)
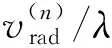
(25)
干扰前、后在40°方位角上的改善因子如图9所示,可以看到干扰后,在杂波凹口外还产生了一个很宽的干扰凹槽,当目标落入该凹槽时,其响应下降将超过25 dB,从而能达到干扰要求。对比图7可以看到相比于伪杂波干扰,基于杂波扩展的投散射干扰大大降低了对目标先验信息准确性的要求。
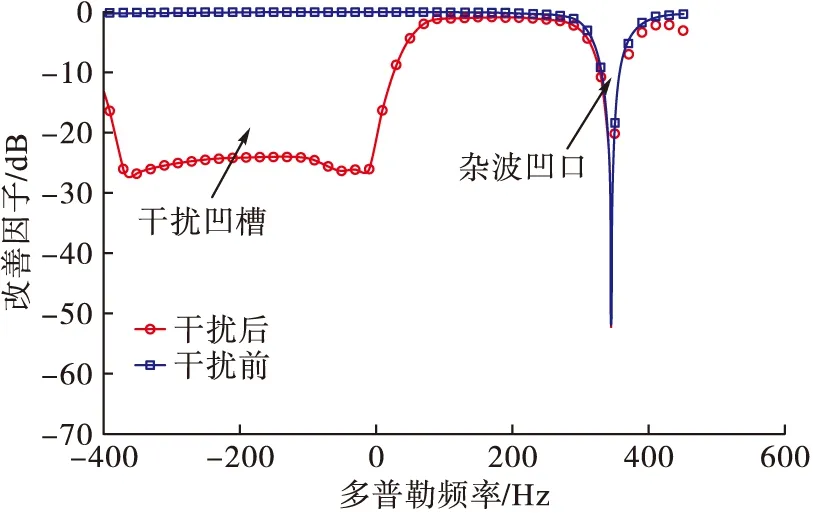
图9 基于杂波扩展的投散射干扰前、后改善因子对比
4 仿真实验
本节主要通过仿真实验比较干扰机接收到的雷达直达波功率和雷达杂波功率,验证截获雷达杂波而非雷达直达波的可行性。通过与伪杂波干扰进行仿真对比验证所提干扰方法的有效性。雷达系统参数由表1给出。
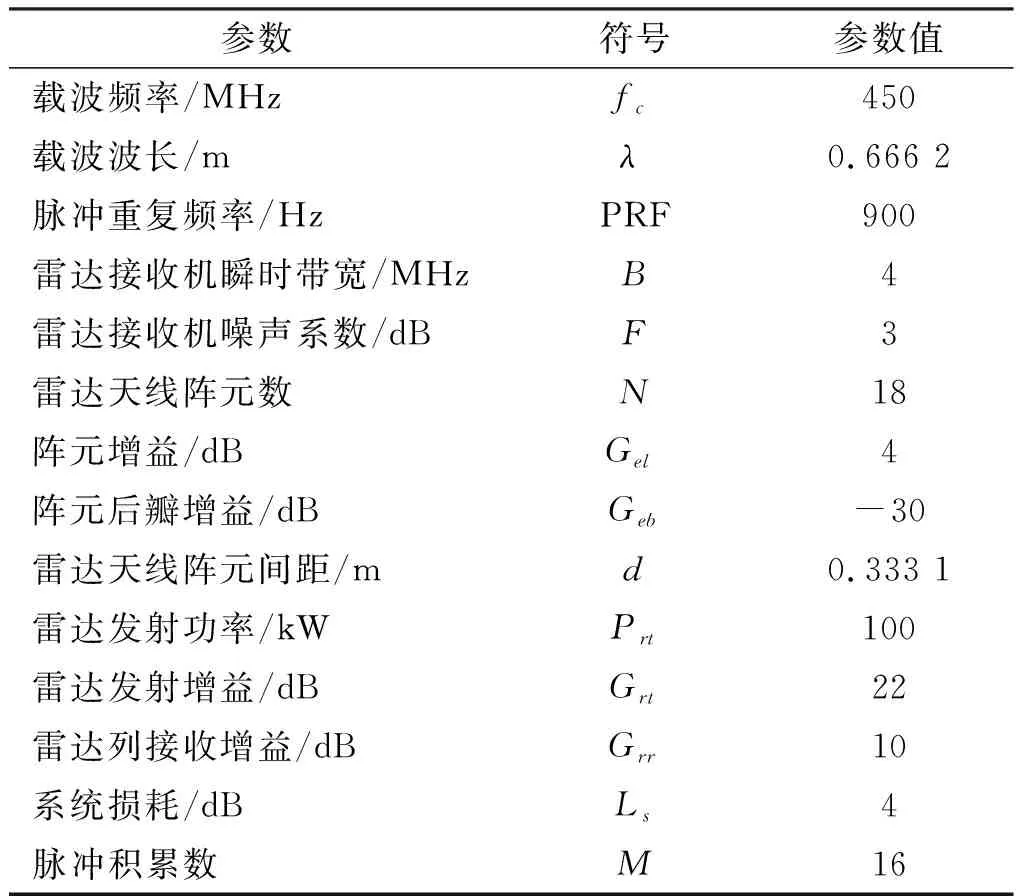
表1 雷达系统参数
基于杂波扩展的投散射干扰将功率分配到NC个子干扰信号上,不妨按角度将NC设为360。干扰机发射功率Pjt为500 W,干扰机发射增益Gjt为18 dB,干扰机天线后瓣增益Gjb为-30 dB,雷达天线阵元和干扰机天线均采用余弦方向图,雷达天线阵元合成的波束指向目标,干扰机天线指向目标所在方位上的伪杂波块,运动平台参数由表2给出,经计算可知目标多普勒频率为-60.041 5 Hz,方位余弦为0.766。

表2 运动平台参数
4.1 功率比较

图11比较了RJ=120 km时干扰机收到的雷达直达波功率和不同地形条件下的雷达杂波功率。随着R2w增大雷达杂波功率减小,由于对偶性,干扰功率也会随着R2w增大而减小,因此选择投射位置时应使R2w尽可能小,此时在几种地形条件下杂波功率均大于直达波功率。这验证了截获雷达杂波信号而非雷达直达波信号的可行性。
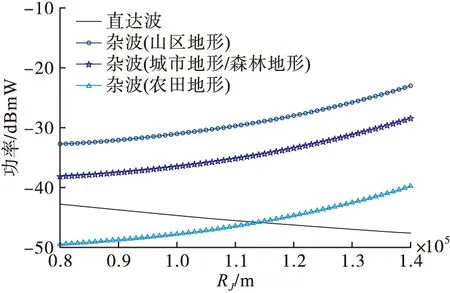
图10 指定R2w下直达波和杂波功率比较

图11 指定RJ下直达波和杂波功率比较
4.2 干扰效果对比
图12是2种干扰条件下雷达STAP处理器目标方位上改善因子的对比,可以看到伪杂波干扰在目标所在的多普勒频率处形成了一个窄而深的凹口,使目标的响应下降了40 dB。基于杂波扩展的投散射干扰则以目标多普勒频率为中心形成一个宽而较浅的凹槽,使宽约0.4归一化多普勒频率(记为F)的多普勒频率范围上的响应均下降了25 dB左右。

图12 干扰后雷达STAP改善因子对比
图13和图14分别是2种干扰后雷达STAP最优响应。图13中伪杂波干扰后,伪杂波凹口覆盖目标,使目标处响应极低,目标多普勒信息和方位信息均被滤除。

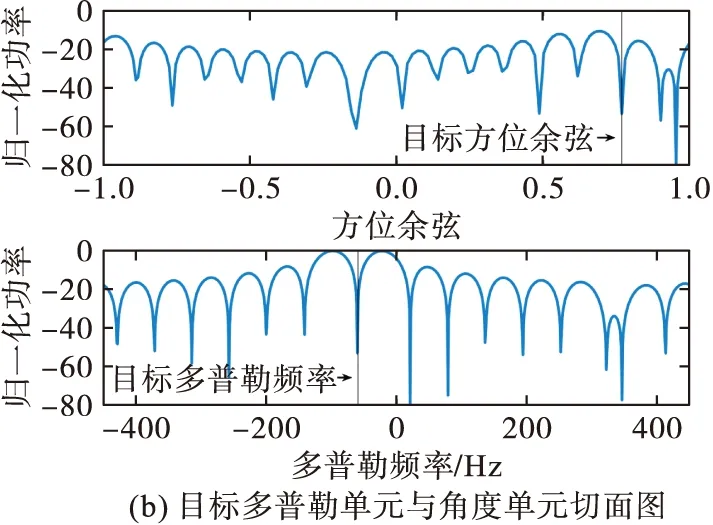
图13 伪杂波干扰后STAP最优响应
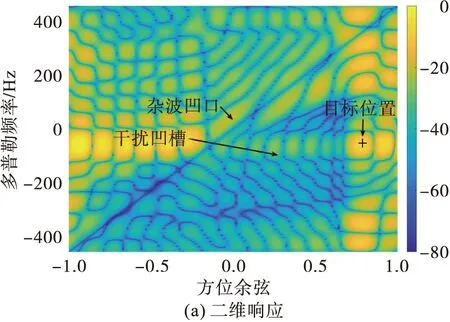
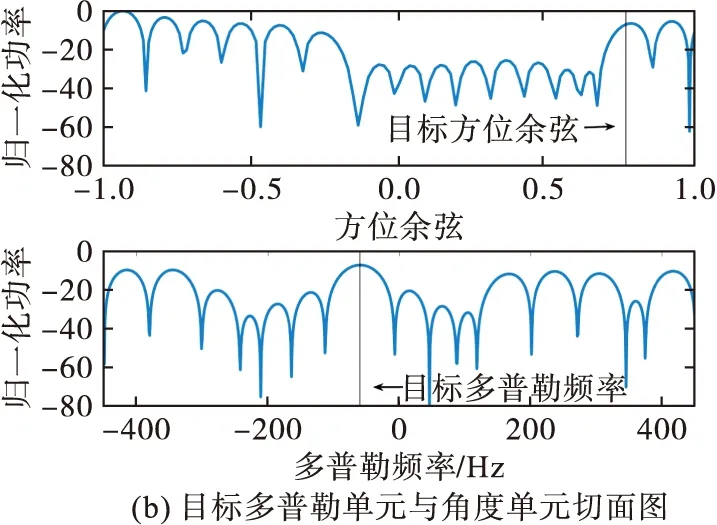
图14 基于杂波扩展的投散射干扰后STAP最优响应
从图14(a)可以看到基于杂波扩展的投散射干扰在目标空时位置附近形成了一个很宽的凹槽,使凹槽内的响应均下降,从图14(b)可以看到干扰后虽然目标处响应仍能取得峰值,但已经不是唯一的峰值,相当于形成了若干假目标,与频移假目标干扰仅能形成多普勒频率上的假目标不同,基于杂波扩展的投散射干扰在方位上也形成了假目标。
从干扰效果来看,伪杂波干扰无疑优于基于杂波扩展的投散射干扰,但伪杂波干扰对先验信息准确度要求较高,图15和图16分别是目标先验多普勒频率信息误差0.03F时2种干扰条件下的STAP最优响应,对比图13和图14可以看出基于杂波扩展的投散射干扰的效果没有变化,而伪杂波干扰效果明显变差,因此,从对目标先验信息误差容错性方面,基于杂波扩展的投散射干扰要优于伪杂波干扰。
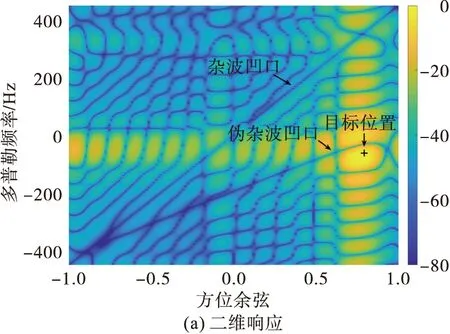
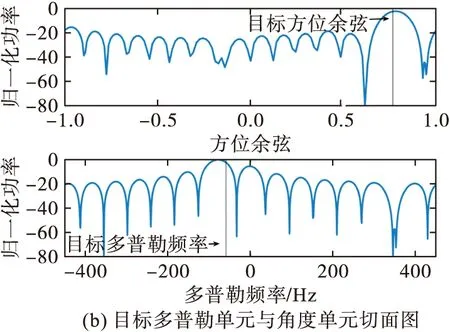
图15 伪杂波干扰后STAP最优响应(误差为0.03F)
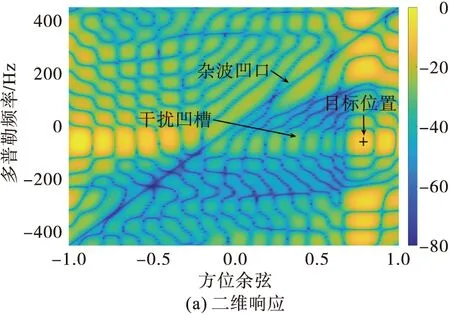
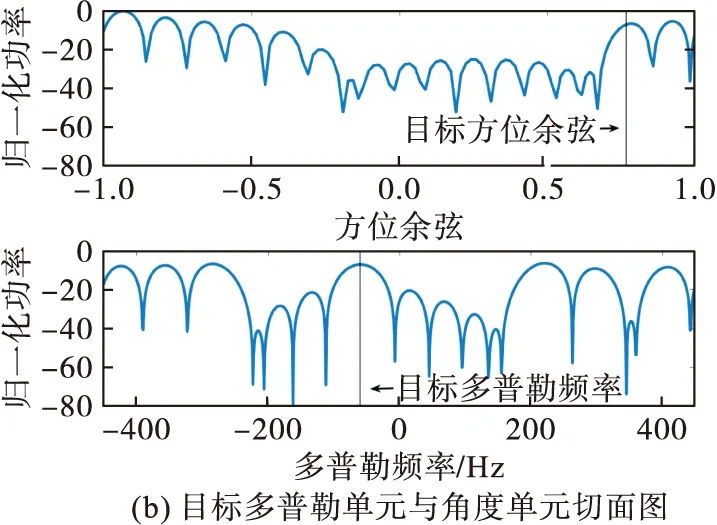
图16 基于杂波扩展的投散射干扰后STAP最优响应(误差为0.03F)
5 结语
本文研究了一种基于杂波扩展的STAP干扰方法。在雷达信号截获方面,对雷达杂波而不是直达波进行截获,解决了在雷达主瓣截获直达波信号被发现概率较大的问题,且杂波信号相当于地面环境对原雷达信号进行了一次调制,保持了相干性,能够获得相干增益,通过仿真比较了干扰机接收到的雷达杂波和直达波的功率,验证了可行性。在干扰时,采用投散射的方式,在雷达副瓣内通过地面散射的方式使干扰信号进入雷达主瓣,形成一个很宽的干扰凹槽,相比于伪杂波干扰,对目标先验信息准确性要求较低,更容易覆盖目标,使目标响应下降,不再是空时平面上的唯一峰值,达到在方位和多普勒频率上均形成假目标的效果。仿真结果验证了这种干扰方法的有效性。在实践中,由于目标准确先验信息并不容易获得,因而基于杂波扩展的投散射干扰较伪杂波干扰更实用,当进一步增加干扰功率时,可以在很宽的频率范围内达到伪杂波干扰的效果。
本文中的干扰方法主要针对传统的STAP技术、考虑到压缩感知理论在STAP中的应用日益增加[15-20],下一步将展开该干扰方法时稀疏恢复STAP技术的干扰效果。
