融合仿真数据的小子样圆概率误差评估
2021-04-08宁小磊吴颖霞赵新
宁小磊, 吴颖霞, 赵新
(中国华阴兵器试验中心, 陕西 华阴 714200)
0 引言
在直升机机载空地导弹、简易制导火箭等装备鉴定和定型试验中,圆概率误差(CEP)作为武器系统攻击精度指标[1],历来备受承试方重视。传统CEP试验方法主要依据现场实弹飞行试验和数理统计理论进行,但随着装备单子样价格的日益昂贵,能够获取的现场实弹数据越来越少。若仍采用传统试验评估方法,则存在CEP评估精度不高的问题。综合应用仿真手段融合评估是解决上述问题的有效途径,但如何融合实弹/仿真数据实现CEP的一体化评估,目前尚未有被各方广泛认同的操作方法[2-4]。
Bayes方法能够充分利用先验信息和现场数据实现参数的后验统计推断[2],因此可以用来融合实弹/仿真数据[3-5],但该方法存在先验分布确定的问题[6-8],当先验信息失真时估计精度甚至下降。目前在试验评估领域使用先验分布的基本条件是仿真数据和实弹飞行数据通过数据相容性检验[9-11]。但在小子样情况下,由于抽样随机性现场试验抽样分布与总体分布很可能存在较大差异,这时即使仿真数据和实弹飞行数据相容性较好,但仍存在仿真先验分布和总体分布不是同一分布的风险,造成“错误”的使用先验分布[7-8]。针对这一问题,文献[10]采用加权自助抽样技术构造了先验分布;文献[6]通过引入修正幂参数构造带幂函数的先验分布,以控制验前信息对验后估计的影响;文献[8]通过加权计算仿真先验分布和无信息先验分布,构造了混合先验分布;文献[5]通过考虑先验信息可信度构造了先验分布,并改进了后验加权系数的计算方法。上述文献针对仿真数据的融合评估,提出了一些科学构造先验分布的改进方法,但本质上都是通过加入无信息先验分布减少仿真先验参加计算后验参数的权重,是一种相对保守的改进策略,并未充分利用先验信息。
针对上述问题,本文提出一种基于“有效样本”的实弹与仿真数据融合算法与小子样CEP评估方法。使用重要性抽样中抽样效率的评估模型度量仿真先验分布与总体分布之间的偏差,确定考虑先验信息有偏差时的先验分布。融合评估时在仿真样本权重的计算上同时依据仿真先验分布与总体分布之间的偏差和样本量调整。当仿真数据不好甚至仿真信息失真时,该方法能够有效避免因仿真数据“淹没”现场数据导致评估结果无效甚至错误的问题。
1 CEP计算及问题分析
1.1 计算CEP的基本方法
以瞄准点或平均弹着点为中心,包含50%弹着点的半径就是CEP,国家军用标准GJB102A-98弹药系统术语和国家军用标准GJB6289-2008地地弹道式导弹命中精度评定方法分别定义了CEP,二者的区别在于是否考虑弹着点的系统误差。通常系统误差比随机误差小且可以修正,因此又近似地把瞄准点作为平均弹着点。
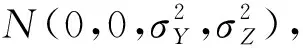
(1)
当σY=σZ=σ时,进行适当变换,可得
CEP=1.177 4σ.
(2)
为了计算CEP,总是估计出未知参数σ后,代入(2)式求取。
1.2 计算CEP的Bayes方法
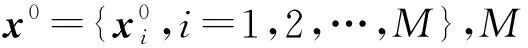
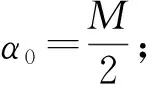
则方差σ2的Bayes估计[2]如下:
1) 当μ已知时,有
(3)

2) 当μ未知时,有
(4)
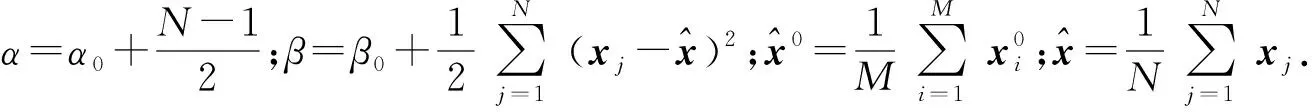
根据上述描述,则CEP的Bayes估计为
CEPB=1.177 4B.
(5)
1.3 问题分析
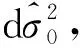
(6)
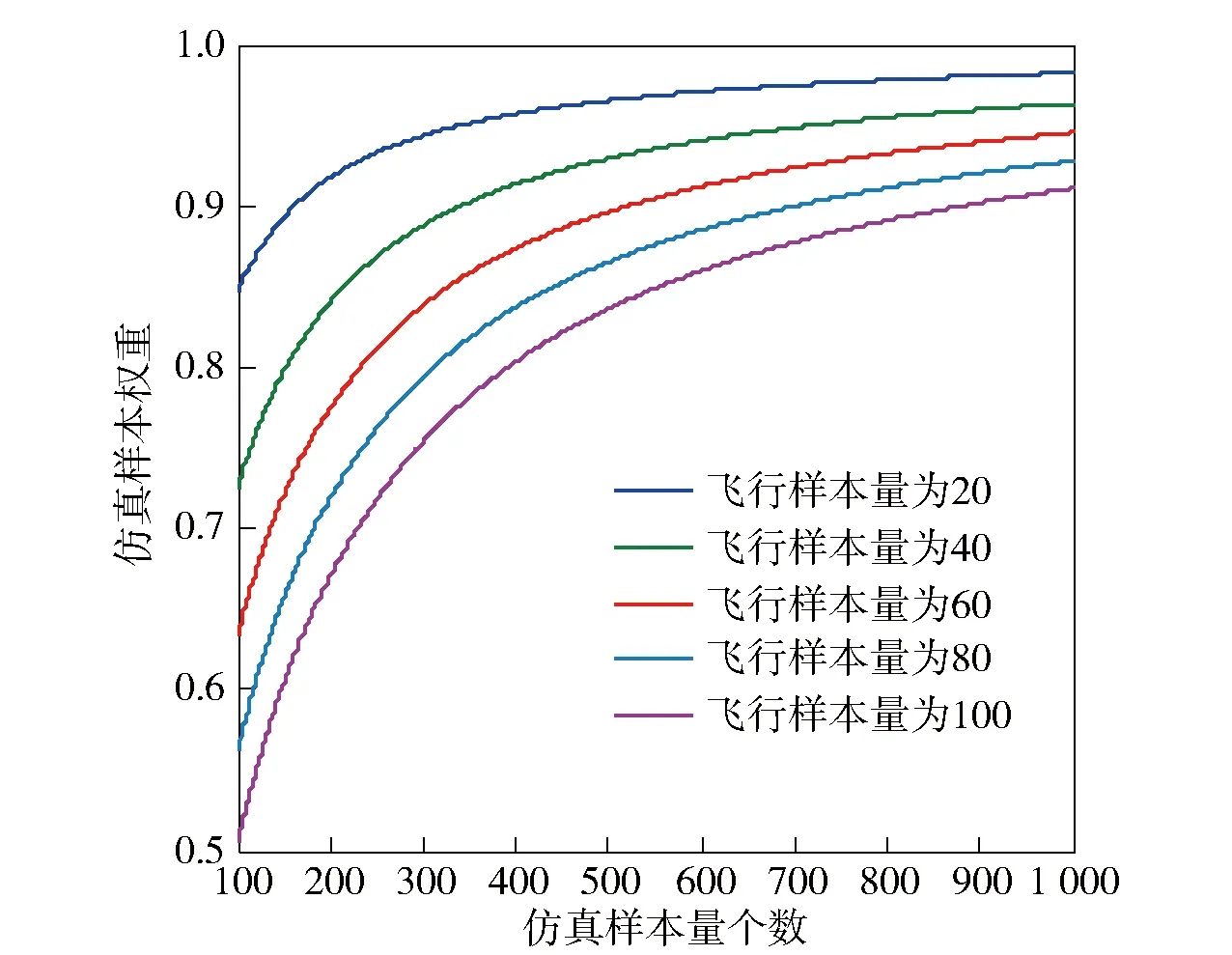
图1 仿真样本权重Fig.1 Weights of simulation samples

图2 CEP估计误差Fig.2 Estimated error of CEP
2 基于重要性抽样确定仿真先验分布
2.1 改进思路
为了防止第1节所述问题发生,一个有效的解决方法是当仿真先验分布与总体分布有偏差时,根据“偏差”修正仿真先验分布,适当调整仿真样本参与Bayes估计的权重,且当两个分布之间的偏差比较小时增大仿真样本权重,当两个分布之间的偏差较大时减小仿真样本权重,从而避免Bayes方法估计时仿真样本权重不受“偏差”的影响,解决仿真数据“淹没”实弹试验数据的问题。
为实现上述改进,需要度量仿真先验分布与总体分布之间的偏差,同时还需要根据这种偏差确定改进后的仿真先验分布,实现仿真样本权重的合理调整。为此,本文提出运用重要性抽样方法中抽样效率的评估模型度量仿真先验分布与总体分布之间的偏差,在此基础上提出一种基于“有效样本”的飞行/仿真数据融合算法与小子样CEP评估方法,根据偏差调整仿真数据参与CEP评估的比例,融合评估时仿真样本权重同时依据仿真先验分布与总体分布之间的偏差和样本量调整。
2.2 基于重要性抽样确定仿真先验分布的应用分析
2.2.1 重要性抽样方法
使用Monte Carlo方法求取如下积分:
(7)
式中:I为积分值;x为积分变量;D为积分区域;h(x)g(x)为被积函数。将被积函数拆分为h(x)和g(x),则h(x)可视为统计量,g(·)为概率分布函数。假设从g(·)中抽取样本x={xk,k=1,2,…,NMC},其中NMC为抽样样本量,则
(8)
为了降低Monte Carlo抽样方差,使计算资源集中在感兴趣的重要区域抽样,减少那些函数值几乎为0对估计结果影响甚微的区域抽样,提出重要性抽样方法[12-13],其主要思想是首先从一个容易抽样的实验分布π(·)中产生独立样本,然后在估计中引入重要性权重来校正偏差,即
(9)
式中:π(·)为重要性分布函数。重要性抽样的另一个好处是当直接从分布函数g(·)中抽样困难(例如抽样消耗大、周期长、过程复杂等情景)甚至是抽样不可能时,重要性抽样方法给出一个可操作的实现(7)式计算的技巧。
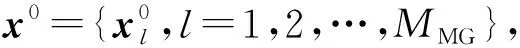
(10)

(11)
式中:x为实际观测数据样本,一般为真实系统输出,是真实值的函数或与真实值相关。文献[13]对(11)式所示重要性权重的高斯分布计算模型合理性进行了讨论,并指出能够反映“加权样本与真值越接近,其权重越大,反之权重越小”这一规律的任何函数都可用来计算重要性权重,只是与(11)式的高斯分布函数相比,没有高斯分布函数平滑[13]。
2.2.2 重要性抽样方法的抽样效率
(12)
式中:u为被估对象估计值;var(·)为方差运算。
(13)
重要性抽样统计量的方差与直接抽样方法统计量的方差之差为
(14)
从(14)式中可见,要求重要性抽样统计量的方差小于直接抽样方法统计量的方差,就需要w(x)=g(x)/π(x)<1,对重要性分布函数的选择提出了理论要求,根据该要求文献[12-13,15-16]给出了最优的重要性分布函数是后验分布函数g(·),但由于真实后验分布函数的形状事前不知道,这个最优的重要性抽样分布只是理论上的。评价抽样方法是有效的,一般可由抽样方法得到的估计量的方差大小进行评定。文献[12,15-16]提出了一种评价重要性抽样的有效方法和衡量重要性分布函数性能的基准量,定义重要性分布函数的相对数值效率(RNE)[16]为
(15)
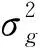
2.2.3 重要性抽样在仿真先验分布确定中的应用
在导弹等高价值类装备鉴定/定型试验中,破坏性实弹飞行试验消耗很大,一般是抽样困难事件或小样本抽样。模拟仿真实验由于其经济性、无破坏性等优势,抽样容易。假设X为实弹飞行试验样本,g(·)为真实分布,可视X为从g(·)抽取的样本,但从g(·)中抽样是困难的高价值事件;X0为仿真实验样本,π(·)为仿真实验分布,可视π(·)为重要性分布函数。根据装备鉴定/定型试验中两种试验手段的特点,可以利用重要性抽样思想,从容易抽样的重要性分布π(·)中抽取大量合适样本,然后在估计中引入实弹飞行样本X和重要性权重w来校正偏差,从而达到提高小样本实验估计精度的目的。
重要性抽样方法在仿真先验分布确定中的应用过程具体如下:抽取仿真样本X0,用实弹飞行试验数据X修正仿真样本估计权重,具体步骤为:
1)计算仿真样本权重。估计均值μ时,重要性权重w为
(16)
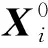
估计方差σ2时,由于σ2=EX2-(EX)2,把X2作为样本观测信息,则重要性权重w为
(17)

2)按(15)式计算仿真样本权重的方差,并计算RNE.
3)计算等效样本KES,公式如下:
(18)
式中:round(·)为取整函数。(18)式可解释为KES个权重样本相当于从目标函数(总体分布)中抽取KES个独立同分布样本。KES称为有效样本或等效样本,就是用一个“虚拟”的抽样样本量表征先验分布精度,或者说是先验分布与总体分布之间的偏差。其工程意义可以解释为从仿真先验分布中抽样,并基于仿真样本进行评估,其评估误差相当于基于KES个实弹试验样本量的评估误差。
KES具备以下基本性质:
1) 当仿真分布与总体分布相同时,KES=M.
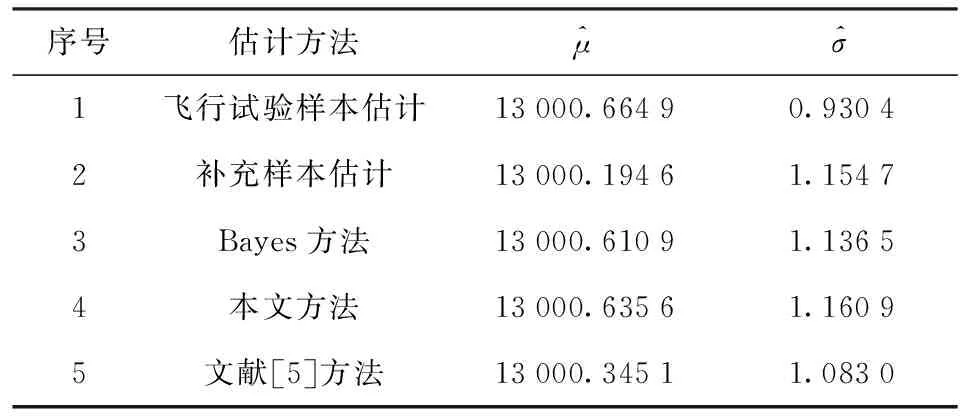
2) 当仿真分布与总体分布有偏差时,KES 3) 0≤KES≤M. 当仿真实验分布与真实分布相同时,仿真样本与飞行样本为独立同分布抽样,样本权重相同。此时w(X)=1,var(w(X))=0,有KES=M,相当于M个实弹样本的估计精度。 使用重要性抽样方法抽样效率模型度量仿真先验分布与总体分布偏差L,将仿真实验样本量M适当地等效为“平行”的实弹飞行试验样本量KES,并由此确定面向试验评估的仿真先验分布如下: IG(α′0,β0), (19) 小子样CEP评估步骤具体总结如下: 步骤2确定仿真先验分布。 通常系统误差比随机误差小且可以修正,因此可以近似地把瞄准点作为平均弹着点,计算时认为μ=0,CEP评估时仅用试验数据估计方差σ2,其共轭先验分布形式如下: IG(α′0,β0). (20) (20)式中超参数α′0的计算过程如下: Forj=1:N fori=1:M (21) end (22) end (23) 则有 (24) 根据(19)式、(24)式,得到先验分布如下: (25) 步骤3根据(3)式,B的Bayes估计为 (26) 步骤4根据(4)式,CEP的Bayes估计为 (27) 采用绝对误差绝对值ECEP、绝对误差方差及均方误差(MSE)等指标,定量对比本文算法和传统方法性能,绝对误差和MSE评价指标计算如下: (28) (29) 图3给出了10次Monte Carlo实验在不同精度(用dσ表示) 仿真先验条件下CEP估计的绝对误差绝对值,模拟计算中现场飞行试验样本量N=10. 从图3中可见,本文方法相比基于飞行样本的估计方法、基于仿真样本的估计方法、Bayes方法在不同精度仿真先验条件下,绝对误差均较小,尤其在仿真先验精度较差的情况下,本文方法的估计精度明显好于Bayes方法,如图3(c)~图3(g)所示。 图3 不同方法求解CEP绝对误差绝对值曲线Fig.3 Estimated errors of CEP of different methods after 10 Monte Carlo tests 图4给出了10次Monte Carlo实验使用不同方法计算CEP的绝对误差和均方误差曲线。由图4可见:基于飞行样本的估计方法精度不受仿真实验影响;随着仿真实验精度变差(标准差误差变大),本文方法、基于仿真样本的估计方法、Bayes方法估计精度均有所下降,但本文方法的估计精度最高,其次是Bayes方法,尤其当仿真先验信息失真时,本文方法仍能够给出保持一定精度的估计结果。由此可见,本文方法在仿真先验信息失真时,估计性能比传统方法明显有优势。同时需要指出,在装备试验与评估领域,提高仿真模型与仿真实验精度以及有效的试验数据融合算法都是提高基于实弹/仿真数据融合综合估计CEP的有效方法。 图4 10次Monte Carlo仿真实验估计误差曲线Fig.4 Absolute value errors and MSEs of 10 Monte Carlo simulation experiments 为了更充分对比算法性能,进行10 000次Monte Carlo实验,实验中模拟现场抽样的样本量N=20. 图5给出了dσ=0.1 m时不同方法的估计误差对比。图6给出了dσ=0.3 m时不同方法的估计误差对比。图7给出了dσ=0.5 m时不同方法的估计误差对比。以上场景分别模拟计算不同精度仿真先验信息情况下不同估计方法的估计精度。为了使结果具有实际意义,评价计算时分别以CEP真值和从总体分布抽样10 000次的大样本统计结果作为对比依据。图5~图7中1代表绝对误差绝对值平均值,2代表绝对误差绝对值方差,3代表MSE. 由图5~图7可见:随着仿真先验分布与总体分布距离偏差变大,基于仿真样本的估计、Bayes估计、本文方法的估计误差均有所增大,但本文方法相比基于仿真样本的估计、Bayes估计方法估计精度下降速率较慢,表明本文方法在仿真先验信息失真时仍能保持一定的精度,估计鲁棒性较好;在dσ=0.1 m时,本文方法10 000次Monte Carlo实验绝对误差的均值、MSE最小,表明本文方法估计精度最高。 图5 dσ=0.1 m估计误差曲线对比图Fig.5 Comparison chart of estimated error curves for dσ=0.1 m 图6 dσ=0.3 m估计误差曲线对比图Fig.6 Comparison chart of estimated error curves for dσ=0.3 m 图7 dσ=0.5 m估计误差曲线对比图Fig.7 Comparison chart of estimated error curves for dσ=0.5 m 为了检验现场抽样样本量对试验评估的影响效应,在dσ=0.1 m条件下进行1 000次Monte Carlo实验,图8给出了不同样本量下的估计误差。从图8中可见:随着飞行样本量的增大,不同估计方法的估计绝对误差、绝对误差方差、MSE均有所减小,且增大到一定数量时各种方法的估计精度基本一致;在小子样情况下,本文方法的估计绝对误差、 图8 dσ=0.1 m时飞行试验样本量与估计误差曲线示意图Fig.8 Comparison chart of estimated error curves in the condition of different flying samples for dσ=0.1 m MSE均较小,表明本文方法在小子样估计精度上的优劣性;小子样情况下,基于仿真样本的估计、Bayes估计方法绝对误差方差最小,这是因为仿真实验的经济性优势可实现大样本抽样,其大样本估计稳定性较好,本文方法绝对误差方差次之,相比基于仿真样本的估计、Bayes估计方法稍大,但仍比飞行试验估计结果小,随着飞行样本量的增大,各种方法绝对误差方差逐渐趋于一致。 表1 不同方法确定的先验分布超参数 表2 不同方法的估计误差对比 案例1[8]在武器落点精度试验中,6个实际纵向落点偏差样本为:X=[0.77 m,5.60 m,14.64 m,-9.79 m,17.6 m,-12.1 m];补充样本为X0=[-11.32 m,-1.65 m, 12.97 m,-27.91 m,-10.88 m,8.32 m,-14.95 m,3.61 m,-5.03 m, 0.28 m]. 采用各种方法得到的估计结果如表3所示。 表3 不同方法给出的估计结果比较 案例2武器落点位置服从正态分布N(μ,σ2),获得飞行试验子样和折合后补充的样本分别为X=[13 000.646 5 km 13 000.385 0 km 12 999.273 9 km 13 001.614 4 km 13 001.404 9 km];X0=[13 002.267 8 km 13 002.575 1 km 12 999.882 1 km 12 999.410 7 km 12 999.346 6 km 13 001.628 5 km 12 997.937 0 km 13 001.209 0 km 13 000.838 0 km 13 000.162 7 km 13 000.324 5 km 12 999.768 4 km 13 000.060 7 km 12 999.316 3 km 13 001.042 7 km 12 999.096 7 km 12 998.676 4 km 12 999.853 4 km 13 000.215 4 km 13 000.281 9 km]。表4给出了直接利用5个飞行试验样本计算、使用补充试验样本计算、经典Bayes估计、本文方法和文献[5]方法(物理可信度p=0.91)的估计结果对比。 表4 不同方法给出的估计结果比较 本文针对仿真数据应用于CEP评估时的问题,提出一种基于“有效样本”的飞行/仿真数据融合算法与小子样CEP评估方法。根据偏差L调整仿真样本权重,当偏差L小时仿真样本权重大,当偏差L大时仿真样本权重小,从而有效解决了仿真数据“淹没”现场实弹数据的问题和仿真先验信息失真时估计效果较差的难题。实验和应用案例表明,在估计精度和稳定性方面,本文方法均具有较好的性能。 参考文献(References) [1] 井沛良, 段宇, 韩超, 等. 基于高斯混合模型和期望最大化算法的非高斯分布圆概率误差估计方法研究[J]. 兵工学报, 2019, 40(2): 369-376. JING P L, DUAN Y, HAN C, et al. Circular error probable estimation method based on Gaussian mixture model and expectation maximum algorithm for non-Gaussian distribution[J]. Acta Armamentarii, 2019, 40(2): 369-376.(in Chinese) [2] 张金槐,唐雪梅.Bayes方法[M].修订版.长沙:国防科技大学出版社,1993:1-3,54-57. ZHANG J H,TANG X M.Bayes method[M].Revised edition.Changsha: National University of Defense Technology Press,1993:1-3,54-57.(in Chinese) [3] 陈维义, 程晗, 刘国强, 等. 考虑仿真可信度的舰炮射击精度贝叶斯估计[J]. 系统工程与电子技术, 2018, 40(11): 2598-2603. CHEN W Y, CHENG H, LIU G Q, et al. Bayesian estimation for naval gun’s firing accuracy considering reliability of simulation[J]. Systems Engineering and Electronics, 2018, 40(11): 2598-2603.(in Chinese) [4] 孙锦, 李国林, 许诚. 基于仿真信息的反舰导弹小子样靶场试验综合评定方法[J]. 系统工程理论与实践, 2014, 34(4): 1077-1088. SUN J, LI G L, XU C. Synthetical evaluation method of anti-ship missile in range trial in condition of small sample based on simulation information[J]. Systems Engineering-Theory & Practice, 2014, 34(4): 1077-1088. (in Chinese) [5] 黄寒砚,段晓君,王正明.考虑先验信息可信度的后验加权Bayes估计[J].航空学报,2008,29(5):1245-1251. HUANG H Y, DUAN X J,WANG Z M. A novel posterior weighted estimation method considering the credibility of prior information[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5):1245-1251.(in Chinese) [6] 杨华波,夏青,张士峰,等.Bayes修正幂验前方法在制导精度评定中的应用[J].宇航学报,2009,30(6):2237-2242. YANG H B, XIA Q, ZHANG S F, et al.A Bayesian modified power prior approach with application in guidance precision evaluation[J].Journal of Aeronautics, 2009, 30(6): 2237-2242. (in Chinese) [7] 段晓君,黄寒砚.基于信息散度的补充样本加权融合评估[J]. 兵工学报, 2007, 28(10): 1276-1280. DUAN X J, HUANG H Y. Weighted Bayesian fusion evaluation based on information divergence of prior sample[J]. Acta Armamentarii, 2007, 28(10): 1276-1280. (in Chinese) [8] 段晓君,王刚.基于复合等效可信度加权的Bayes融合评估方法[J].国防科技大学学报,2008,30(3):90-94. DUAN X J, WANG G. Weighted Bayesian fusion evaluation basing on composite equivalency model [J].Journal of National University of Defense Technology, 2008,30(3):90-94.(in Chinese) [9] 杨华波,张士峰,蔡洪.利用构造性仿真进行导弹精度评估[J].国防科技大学学报,2005,27(2):27-30. YANG H B, ZHANG S F, CAI H. Evaluation of missile precision by using construction simulation[J]. Journal of National University of Defense Technology, 2005, 27(2): 27-30. (in Chinese) [10] 闫志强,蒋英杰,宫二玲, 等.基于修正权值混合验后的导弹精度融合评估[J].系统工程与电子技术, 2011, 33(3):712-716. YAN Z Q, JIANG Y J, GONG E L, et al. Synthetic evaluation of missile precision based on mixed posteriors with modified weights[J]. Systems Engineering and Electronics,2011,33(3):712-716. (in Chinese) [11] 唐雪梅,张金槐,邵凤昌.武器装备小子样试验分析与评估[M].北京:国防工业出版社, 2001: 1-3. TANG X M, ZHANG J H, SHAO F C. Test analysis and evaluation of weapon systems in small-sample circumstances[M]. Beijing: National Defense Industry Press, 2001: 1-3. (in Chinese) [12] 梁彦,潘泉,杨峰,等.复杂系统的现代估计理论及应用[M].北京:科学出版社,2009:170-177. LIANG Y, PAN Q, YANG F,et al. Model estimation theory of complex system and its application[M]. Beijing: Science Press, 2009:170-177. (in Chinese) [13] 黄小平,王岩,缪鹏程.粒子滤波原理及应用[M].北京:电子工业出版社,2017:89-92. HUANG X P, WANG Y, MIU P C. Particle filter principle and applications [M].Beijing: Publishing House of Electronics Industry, 2017:89-92. (in Chinese) [14] 郭永红,宋彪,赵东阳,等. 基于极限学习机模型的粒子滤波无设备定位方法研究[J].兵工学报,2019,40(8):1740-1746. GUO Y H, SONG B, ZHAO D Y, et al. Research on extreme learning machine model-based particle filter tracking method for device-free localization[J]. Acta Armamentarii, 2019, 40(8): 1740-1746. (in Chinese) [15] 刘军.科学计算中的蒙特卡罗策略[M]. 北京:高等教育出版社, 2013:23-29. LIU J. Monte Carlo strategy in scientific calculation[M]. Beijing: Higher Education Press, 2013:23-29. (in Chinese) [16] GEWEKE J. Bayesian inference in econometrics model using Monte Carlo integration[J]. Econometrica, 1989, 57(6): 1317-1339.2.3 基于重要性抽样确定的仿真先验分布

3 融合仿真数据的小子样CEP评估步骤

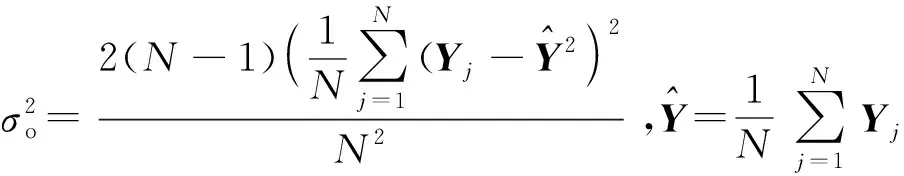
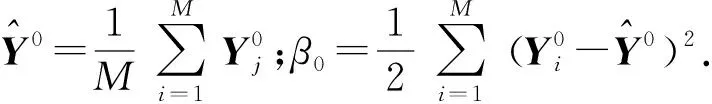
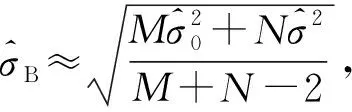
4 仿真实验与分析
4.1 场景描述

4.2 仿真结果与分析



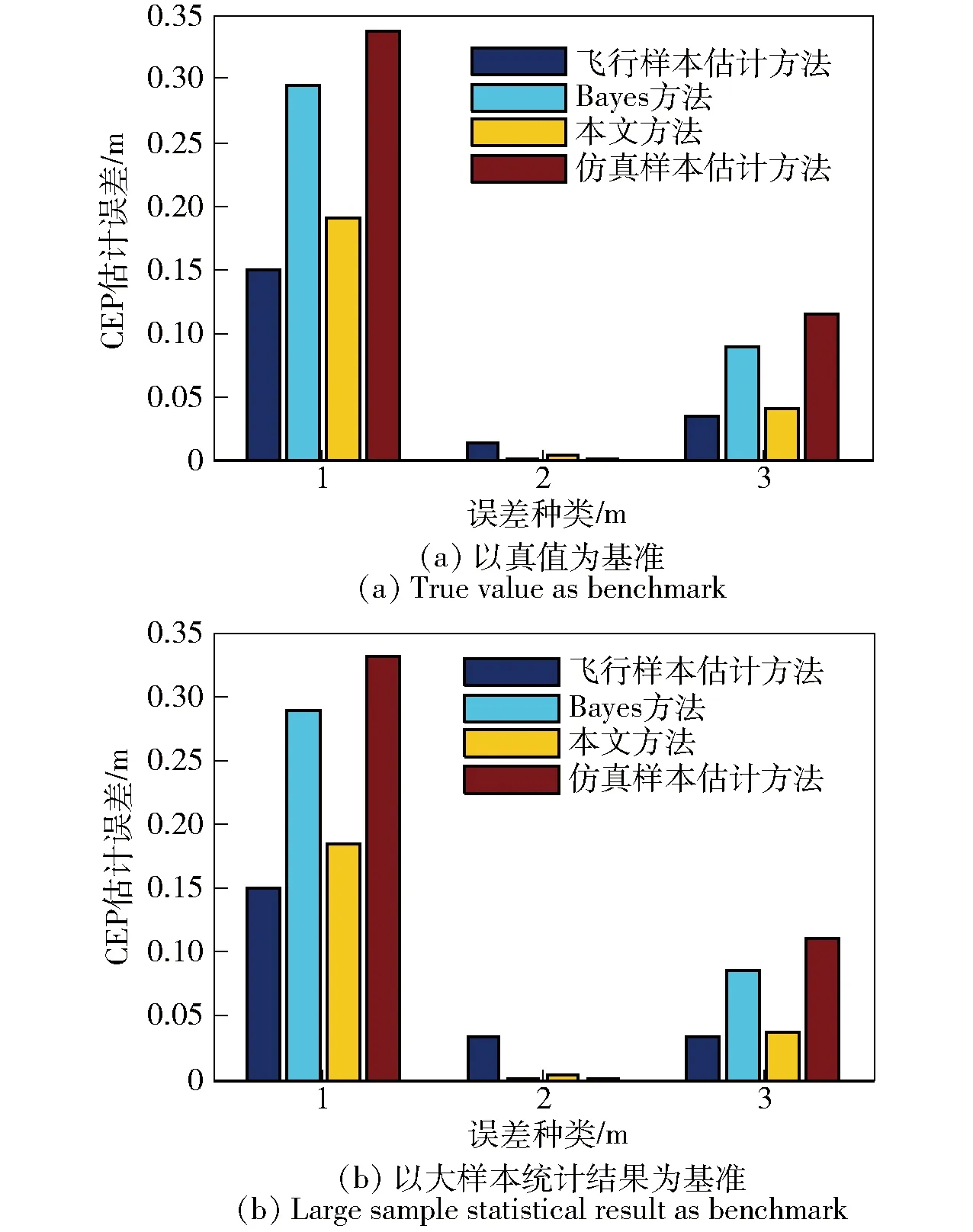
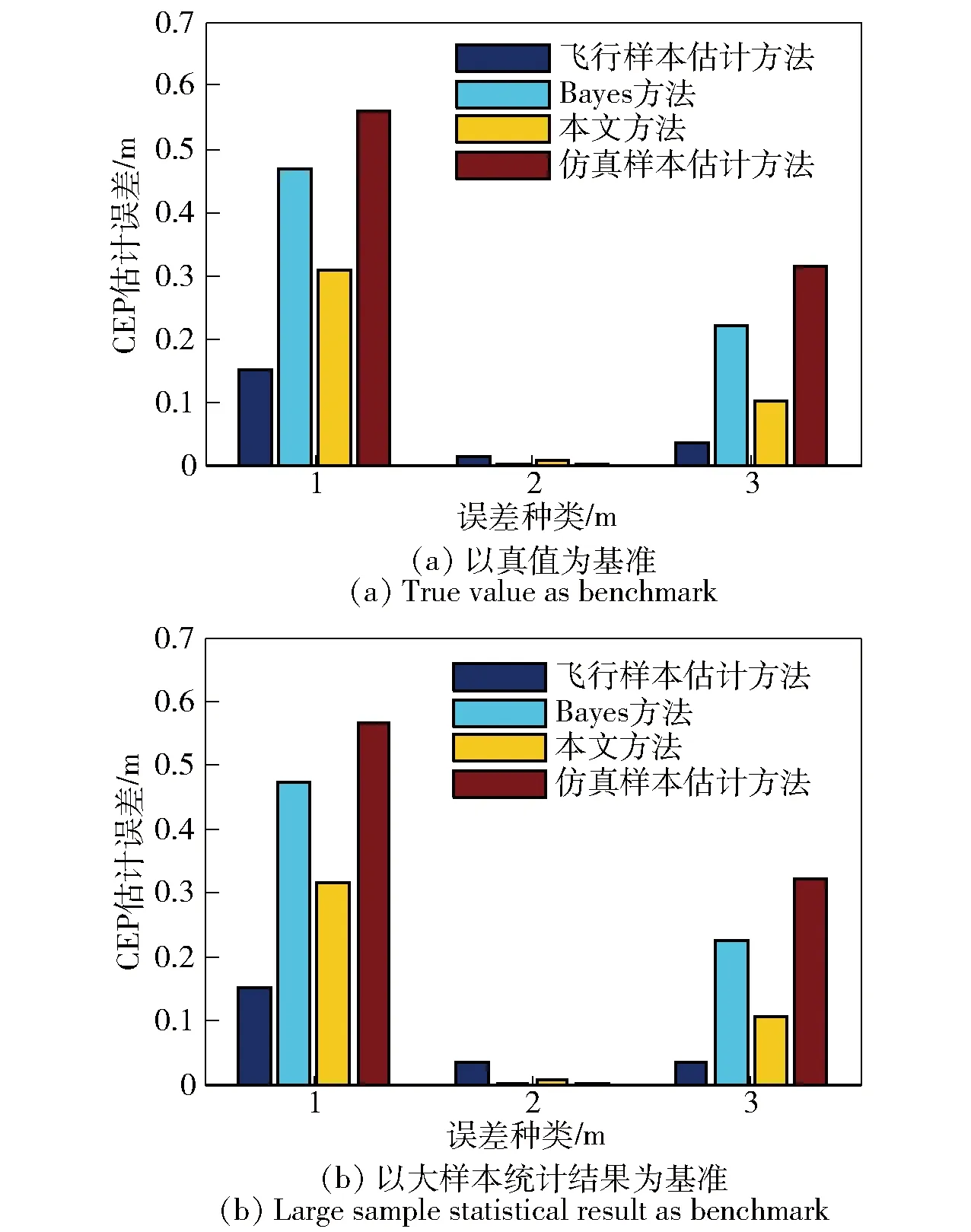
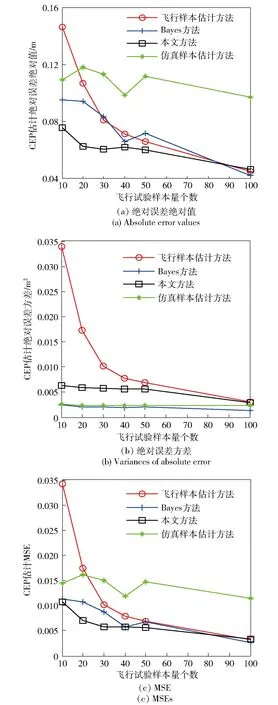



5 应用案例
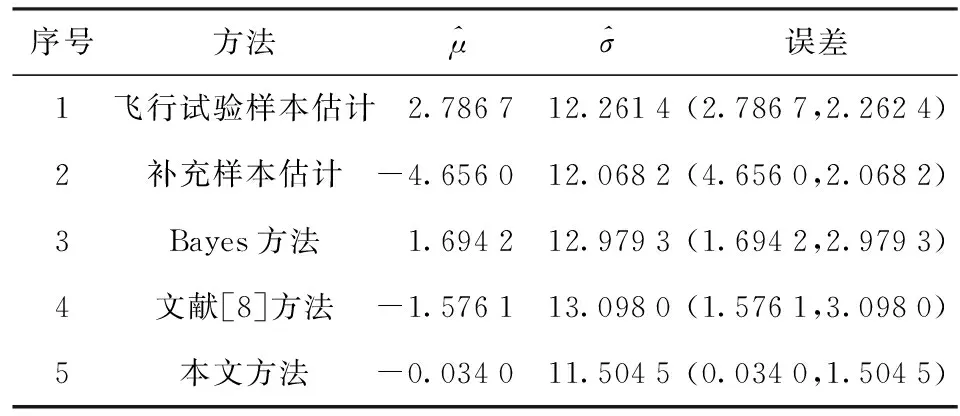
6 结论
