弹丸初速可调的电磁轨道炮对空射击策略

张志勇， 王团团， 郭浩， 王亚飞

(江苏自动化研究所, 江苏 连云港 222006)

0 引言

电磁轨道炮具有初速快、射程远、威力大、精度高等优良特性[1]，已逐渐应用于对海攻击、对岸火力支援和近程防空反导等多种作战任务。不同于传统火炮，电磁轨道炮通过磁场与电流相互作用产生强大的电磁能推动弹丸出炮口[2-3]，弹丸初速可调，进而改变传统舰炮对目标的打击方式，如单炮多发同时弹着[4-5]以提高命中精度和火力密度。

针对舰炮弹丸初速可调，卢发兴等[6]利用Cramer-Rao下界理论推导出弹丸初速对预测目标位置误差影响的解析方程，定量评估了提高舰炮初速能够明显降低命中点预测误差。许俊飞等[7]对不同初速下新型舰炮的能力指标变化趋势进行了研究，发现对近距离目标，初速越大，单发命中概率越好，而距离较远时，初速的优势体现则不明显。吴威等[8-9]建立了弹丸对海上目标的命中概率模型，分析弹丸初速对目标命中概率的影响，证实对视距内海上目标存在最佳弹丸初速使命中概率最大并提出一种基于最大命中概率的射击诸元解算方法。Gallant等[10]使用7管“守门员”舰炮连续发射质量0.14 kg、弹径25 mm的弹丸，通过控制不同弹丸的初速可实现多弹同时打击来袭亚音速反舰导弹，实现大概率命中。

然而目前关于弹丸初速对目标命中概率影响的分析多集中在对海低速运动目标、单发射击上，缺乏对空中高速运动目标、全航路上连续射击的指挥决策研究。本文通过建立弹丸六自由度外弹道运动方程组以及弹丸对空中目标的命中概率模型，系统地分析了单管中口径电磁轨道炮单发射击、全航路连续射击下目标距离、弹丸初速对目标命中概率的影响，并据此提出一种射击策略可兼顾全航路累积命中概率和打击成本，为后续的射击指挥决策研究奠定基础。

1 命中概率模型

开展装备战斗损伤规律的研究，对提升部队实战化水平，打赢高新技术背景下的现代战争具有十分重要的意义[11]。电磁轨道炮弹丸动能大，可直接命中目标进行毁伤[12]。为简化运算，假设以水平矩形目标中心为瞄准点，得到目标命中界为Lx×Lz，Lx为x轴上命中边长，Lz为z轴上命中边长，且x轴和z轴上的随机误差分量相互独立(舰炮指向目标未来点方向为x轴，z轴垂直于x轴，目标水平向左为正)，则发射1发弹丸的命中概率[13]为

(1)

式中：φ(x)、φ(z)分别为弹着散布误差在x轴、z轴上的正态分布密度函数，即

(2)

ρ=0.476 9为正态常数，Sx为x轴系统误差，Ex为x轴随机误差。依据参考文献[9]确定Sx、Ex如下：

Ex=kEx·d，

(3)

(4)

式中：kEx为距离误差系数；d为目标命中距离；kSx为系统误差系数；Dx(T+η·T)为目标运动要素估计误差精度下限的x轴预测位置误差；T为滤波时间；η为预测时间参数，η=tf/T，tf为弹丸飞行时间。

(5)

式中：σx为x轴观测误差；Ti为数据采样间隔时间。

类似可得φ(z).

则对一个提前点发射n发的累积命中概率为

Pa=1-(1-P)n,n=1,2,3,…，

(6)

式中：P为该提前点上弹丸的单发命中概率。

对目标全航路发射n发的累积命中概率为

Pa=1-∏(1-Pni)，

(7)

式中：Pni为发射第n发弹丸对应的提前点i上的目标命中概率。

2 六自由度弹道方程

电磁轨道炮外弹道模型描述了弹丸离开炮口在大气中飞行的过程，考虑电磁轨道炮弹丸大射程、超高速飞行的特点，建立电磁轨道炮弹丸的刚体六自由度运动方程组[14-15]。模型建立中采用4个参考坐标系[16]：地面坐标系Axyz、弹体坐标系OxByBzB、弹道坐标系OxTyTzT和速度坐标系Oxvyvzv.

将弹丸质心动力学方程投影到弹道坐标系：

(8)

式中：FxT、FyT、FzT为电磁轨道炮合外力在弹道坐标系3个坐标轴上的分量；θ为弹道倾角；ψv为弹道偏角；m为弹丸质量；v为弹丸速度。

弹丸绕质心的动力学方程投影到弹体坐标系：

(9)

式中：JxB、JyB、JzB，ωxB、ωyB、ωzB，MxB、MyB、MzB分别表示弹体坐标系下的转动惯量、转动角速度和弹丸受到的合力矩。

在地面坐标系中建立弹丸的质心运动学方程和绕质心运动学方程，即(10)式，其中ϑ为俯仰角，ψ为偏航角，γ为倾斜角。为闭合方程组，根据地面坐标系、弹体坐标系、弹道坐标系和速度坐标系的几何关系[17]，可得几何关系方程(11)式，其中α为攻角，β为侧滑角，γv为速度倾斜角，(8)式～(11)式组成了电磁轨道炮弹丸外弹道运动方程组。

(10)

(11)

3 目标与弹丸相遇问题

对视距内同一个来袭目标进行打击，不同的目标距离和弹丸初速确定不同的弹丸外弹道。本文采用由近及远的改进迭代解命中方法，首先根据射击区间能力确定最近的目标打击距离，再利用给定的弹丸初速求取弹丸飞行时间并逐次反推弹丸与目标的相遇点。具体实施如下：

步骤1令Lmin为射击近界，Lmax为射击远界，射击区间为[Lmin，Lmax]，弹丸初速为v0，目标位置速度信息已知，则弹丸与目标的最近相遇点在射击近界Lmin上，弹丸飞行时间为tf0；

步骤2根据tf0确定射击时刻目标所在位置，以斜距离D0进行表示；

步骤3根据弹丸初速反求电磁轨道炮充电时间，确定每次射击时刻对应的目标斜距离D1、D2、D3…Dn；

步骤4令电磁轨道炮直瞄目标现在点D1，其弹丸飞行时间为tD1，计算目标D1经tD1/2时间后的斜距离为Di1，直瞄Di1对应的弹丸飞行时间为tDi1；

步骤5计算目标D1经(tD1/2 +tDi1)/2时间后斜距离为Di2；

步骤6若|Di1-Di2|>0.01 m，则认为弹丸与目标未相遇，计算直瞄Di2对应的弹丸飞行时间tDi2；

步骤7令Di1=Di2，计算目标D1经(tDi1+tDi2)/2时间后斜距离为Di2. 若|Di1-Di2|≤0.01 m，则认为弹丸与目标相遇，此时相遇点斜距离Dc1=Di2，同样方式确定Dc2、Dc3、…、Dcn；否则重复步骤5～步骤7，直到满足条件。

4 仿真结果分析

对于弹丸初速可控的舰炮，对目标进行打击时，可根据目标的远近，选择不同的弹丸初速以实现大概率命中目标的目的。首先分析单发射击、全航路连续射击下目标距离对命中概率的影响；然后讨论弹丸初速对目标命中概率的影响；最后重点分析如何在全航路上动态调整弹丸初速以达到较大的目标命中概率。

4.1 计算条件

假设某空中目标在x轴投影长度为12 m，在z轴投影长度为10 m. 目标速度vt=300 m/s，飞行高度H=100 m，捷径为0 m，俯冲角为0°. 滤波时间T=2 s，数据采样间隔ti=0.01 s. 观测误差σx=20 m，σz=15 m，随机误差系数kEx=1/300 rad，kEz=1×10-3rad，系统误差系数kSx=kSz=2.

根据美国海军研究署发布信息，电磁轨道炮可在32 MJ出口动能条件下，实现最大10发/min的射速。另外，其发布电磁轨道炮超高速射弹(HVP)的弹丸初速最大马赫数可达7，最大射程超过185 km，弹长609.6 mm，弹质量12.71 kg，杀伤方式为动能杀伤，本文根据其发布的HVP弹信息进行仿真计算。为方便讨论，对电磁轨道炮充电发射过程理想化如下：

1) 充电时间与出口动能为线性关系，且充电6 s，出口动能32 MJ；

2) 电磁轨道炮发射理想化，可持续无间断射击，即充电的同时亦可对目标进行打击且无延迟；

3) 电磁轨道炮连续射击间无扰动量。

根据上述假设，可得射速Fr、充电时间td和初速v0数学模型如下：

(12)

式中：floor()为向下取整函数。

4.2 目标距离

根据常规中大口径火炮初速为800～1 000 m/s、美海军发布HVP信息以及文献[9-10]，最终确定丸初速v0在1 000～2 300 m/s之间变化。

固定两弹丸初速为v1、v2(v1、v2为常值)，求单发射击下命中概率随目标距离变化规律，如图1所示，其中，v2>v1，L为目标距离。由图1可知，在不同弹丸初速下命中概率随目标距离增大而减小，在较小的目标距离下命中概率减小的幅值更大。另外在目标距离L位于500～8 000 m之间时，P(v0=v2)>P(v0=v1).

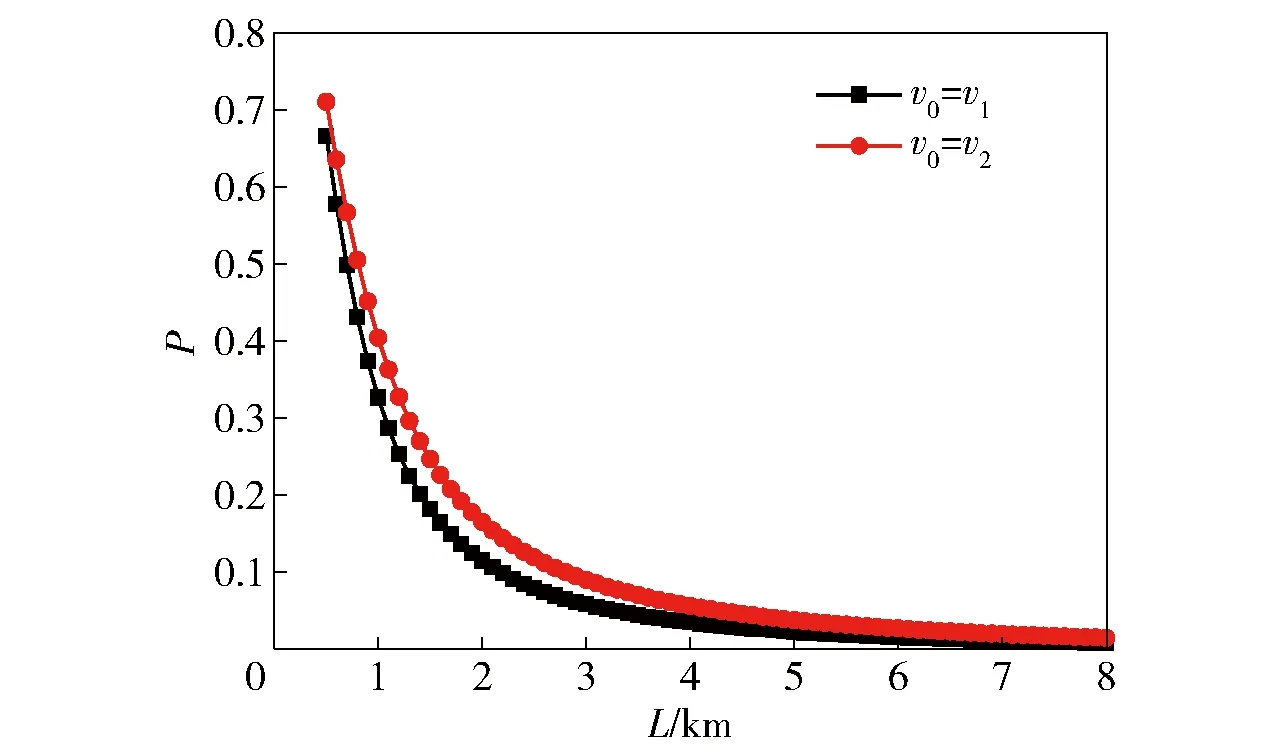
图1 单发射击下命中概率随目标距离变化曲线图Fig.1 Changing curves of hit probability with target distance during single-shot firing

当目标距离大于5 000 m后，目标距离对命中概率的影响已非常小，对目标的打击成本明显增大，故对超视距目标进行打击时，无控弹丸不能获得较好效果，应采用新型信息化制导弹丸以提高弹丸的命中率。

在全航路连续射击中，固定弹丸初速为v1，采用由近及远的解命中策略解算射击区间在1 000～6 000 m的目标累积命中概率，如表1所示。由表1可知：在全航路连续射击状态下，目标累积毁伤概率为58.26%；另单次射击中，目标距离越远，命中概率越小。图2为射击区间大小Ld=5 000 m、全航路连续射击下目标累积命中概率随射击近界的变化曲线图。由图2可知，与单发射击类似，在不同弹丸初速下目标全航路累积命中概率随射击近界的距离增大而减小，且在较小的射击近界距离下累积命中概率减小的幅值更大。

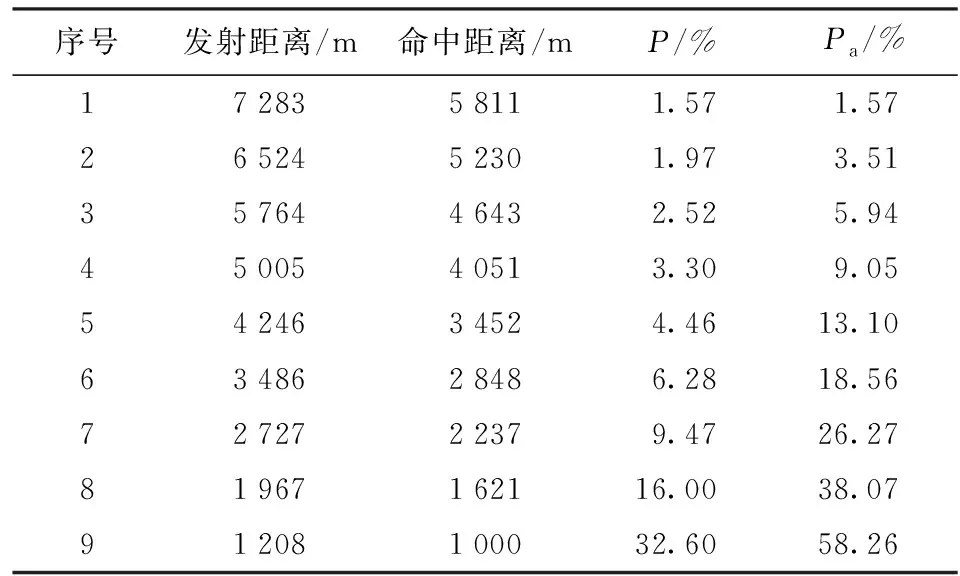
表1 v0=v1、Lmin=1 000 m、Ld=5 000 m下全航路目标命中参数

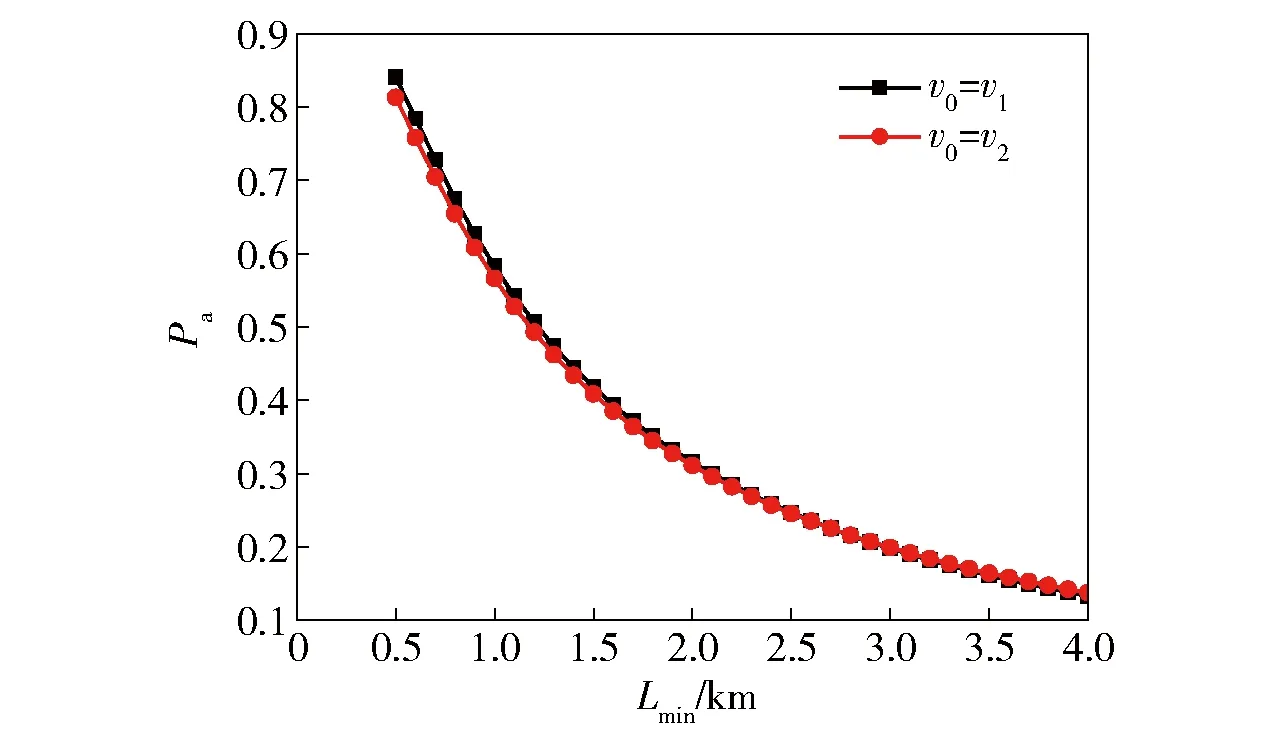
图2 Ld=5 000 m、全航路连续射击下累积命中概率随射击近界变化曲线图Fig.2 Changing urves of cumulative hit probability with Lmin under the conditions of whole-route continuous firing and Ld=5 000 m

故不论在单发射击还是全航路连续射击的指挥决策中，应首先保障在对空防卫射击近界上对来袭目标进行火力打击。

与单发射击不同的是，在全航路连续射击过程中，射击近界Lmin≈2 750 m时，Pa(v0=v2)=Pa(v0=v1)，即在Lmin<2 750 m时，并非弹丸初速越大，全航路累积命中概率越大。

4.3 弹丸初速

根据4.2节可知，Ld=5 000 m、全航路连续射击下存在Lmin=2 750 m，使得全航路累积命中概率Pa(v0=v2)=Pa(v0=v1)。为进一步讨论弹丸初速对目标命中概率的影响，令射击区间大小Ld=5 000 m，射击近界Lmin分别为2 000 m、3 000 m和4 000 m，研究全航路连续射击中弹丸初速变化对目标命中概率的影响。图3显示了Ld分别为5 000 m，Lmin分别为2 000 m、3 000 m和4 000 m，全航路连续射击下最后一发命中概率Pn、累积命中概率Pa和射击发数n与弹丸初速v0的关系曲线。由图3可知：在单发射击，同一个目标距离下Pn随弹丸初速增大而增大；而在Ld=5 000 m的3个射击区间内，全航路连续射击状态下，Pa随着弹丸初速整体趋势上先增大、后减小，在弹丸初速增大过程中，受射击发数的减小出现阶跃下降再逐渐增大的变化现象，出现多个概率极小值；另外在相同弹丸初速下，Pa(Lmin=2 000 m)>Pa(Lmin=3 000 m)>Pa(Lmin=4 000 m)。

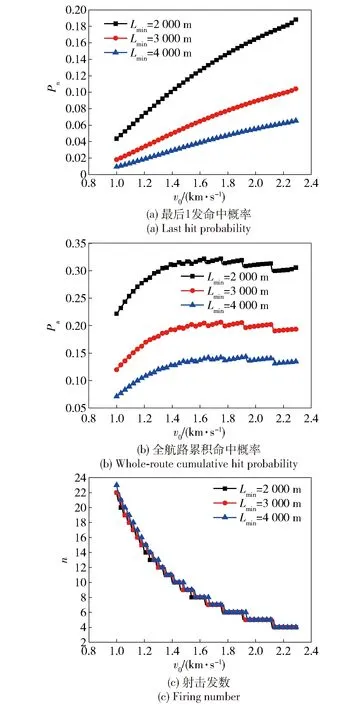
图3 Ld=5 000 m、不同射击近界、全航路连续射击下目标命中参数随弹丸初速变化曲线图Fig.3 Changing curves of cumulative hit probability with muzzle velocity under the conditions of whole-route continuous firing, Ld=5 000 m and different Lmin

图4显示了Lmin=2 000 m，Ld分别为2 000 m、5 000 m、8 000 m 3种射击区间下，全航路累积命中概率与弹丸初速的关系曲线。由图4可知：当射击近界相同，射击区间较小时，全航路射击发数较少，且目标距离较近，射击远界附近的单发命中概率较大，全航路累积命中概率受射击发数的影响较大，故在弹丸初速增大中，全航路射击发数减小，其累积命中概率出现较大阶跃幅度的下降；而当射击区间大小增大到一定程度，射击远界附近的单发命中概率已极小，射击发数对全航路累积命中概率的影响明显减小。

图4 Lmin=2 000 m、不同射击区间大小、全航路连续射击下累积命中概率随弹丸初速变化曲线图Fig.4 Changing curves of cumulative hit probability with muzzle velocity under the conditions of whole-route continuous firing, Lmin=2 000 m and different Ld

故在较小的射击近界和射击区间下，应合理调整全航路弹丸初速，避免陷入累积命中概率局部极小值。

4.4 射击策略

由图3(c)可知，随着弹丸初速的增加，在目标来袭过程的射击发数逐渐减少。在Lmin=2 000 m、Ld=5 000 m，弹丸初速最大时，即v0=2 300 m/s，射击发数为4发，其目标命中参数如表2所示。由表2可看出，全航路累积命中概率为30.63%。因累积命中概率同时受目标距离、弹丸初速和射击发数的影响，在全航路连续射击中，并非弹丸初速越大越好，应综合考虑目标距离、弹丸初速和射击发数以获得较优的射击策略。

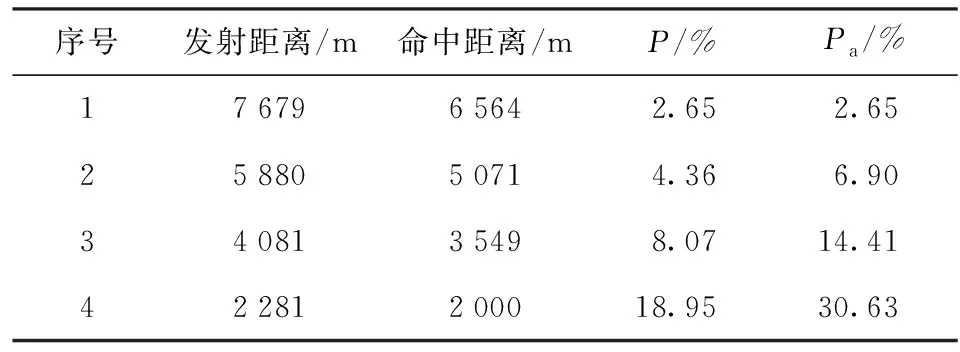
表2 v0=2 300 m/s、Lmin=2 000 m、Ld=5 000 m下全航路目标命中参数

首先选定3类典型速度模型如下：

(13)

v0=C,C为最优常值；

(14)

(15)

式中：j表示发射的第j发弹丸，为无量纲变量；速度模型2((14)式)中的C表示全航路连续射击，弹丸初速固定不变情况下，其值为C，累积命中概率最大。图5显示了速度模型1((13)式)和模型3((15)式)的变化规律，从中可看出：在速度模型1中，目标距离越近，弹丸初速越大；而速度模型3与之相反。

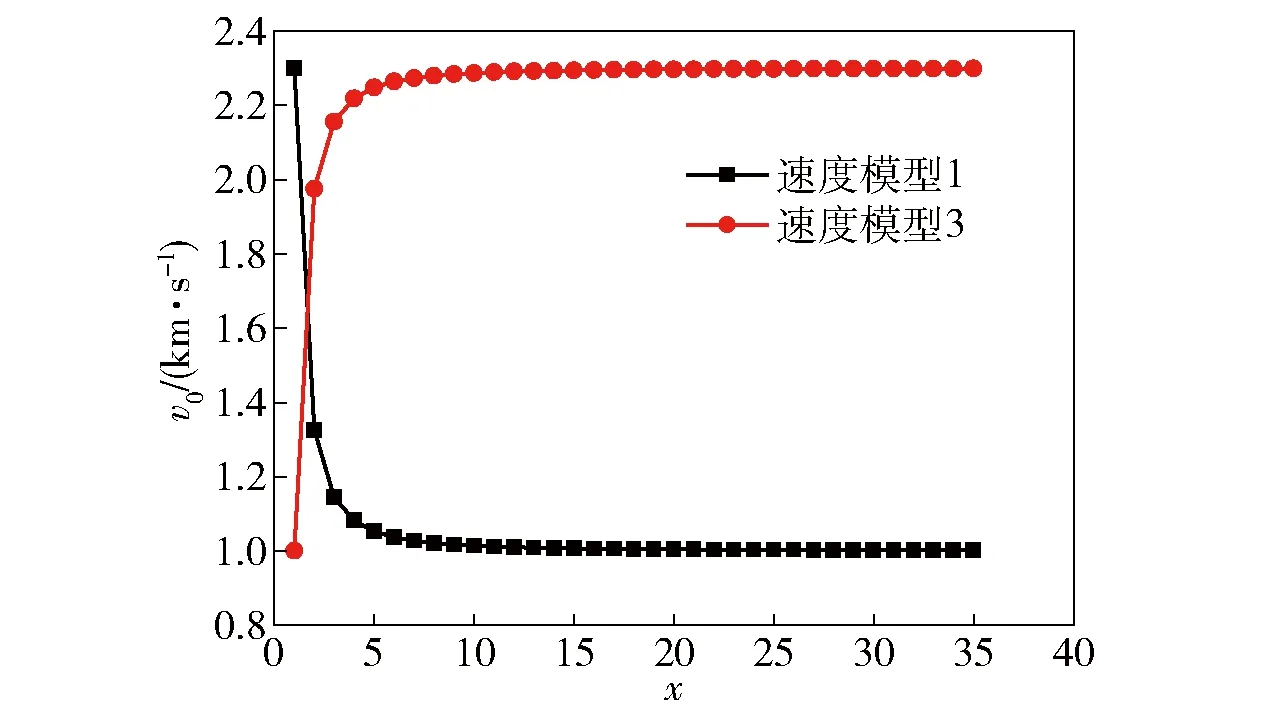
图5 速度模型1和模型3示意图Fig.5 Schematic diagram of speed models 1 and 3

为比较3种速度模型的射击策略优劣，计算Lmin=2 000 m，射击区间大小逐渐增大时3种速度模型下的命中参数如图6所示。由图6可知：速度模型3的射击策略中，全航路累积命中概率明显较低，而速度模型1的射击策略中，累积命中概率远大于后二者，但全航路射击发数较大，尤其在较大的射击区间下，打击成本相对较大；而速度模型2的射击策略中，其累积命中概率和打击成本介于二者之间。

图6 Lmin=2 000 m、不同速度模型、全航路连续射击下目标命中参数随射击区间大小变化曲线图Fig.6 Changing curves of target hit parameters with Ld under the conditions of whole-route continuous firing, Lmin=2 000 m and different speed models

为了兼顾全航路累积命中概率和打击成本，本文提出由近及远、有效射程内单发命中概率最大、射击远界同时弹着的射击策略，即：在射击区域内每一次射击下，确定一弹丸初速，使得该次射击中弹丸命中概率最大；而在射击远界附近，通过控制弹丸初速令多发弹丸同时弹着以提高命中率。在此称其为平衡射击策略。

为与上述3种速度模型对应下的射击策略对比，令射击区间相同，采用平衡射击策略方法，得结果如图7所示。由图7可知：与速度模型2射击策略相比，其射击发数基本相同，但全航路累积命中概率明显增大，接近于速度模型1，如表3中Ld=5 000 m对应的全航路命中参数，此时射击发数为8，累积命中概率Pa=34.66%；在相同条件，采用速度模型1对应的射击策略，虽累积命中概率Pa=37.82%，但其射击发数n=21，打击成本较大；采用速度模型2对应的射击策略，射击发数n=7，但累积命中概率Pa=32.18%，低于平衡射击策略的Pa.

图7 Lmin=2 000 m、平衡射击策略、全航路连续射击下目标命中参数随射击区间大小变化曲线图Fig.7 Changing curves of target hit parameters with Ld under the conditions of whole-route continuous firing, Lmin=2 000 m and balanced shooting strategy

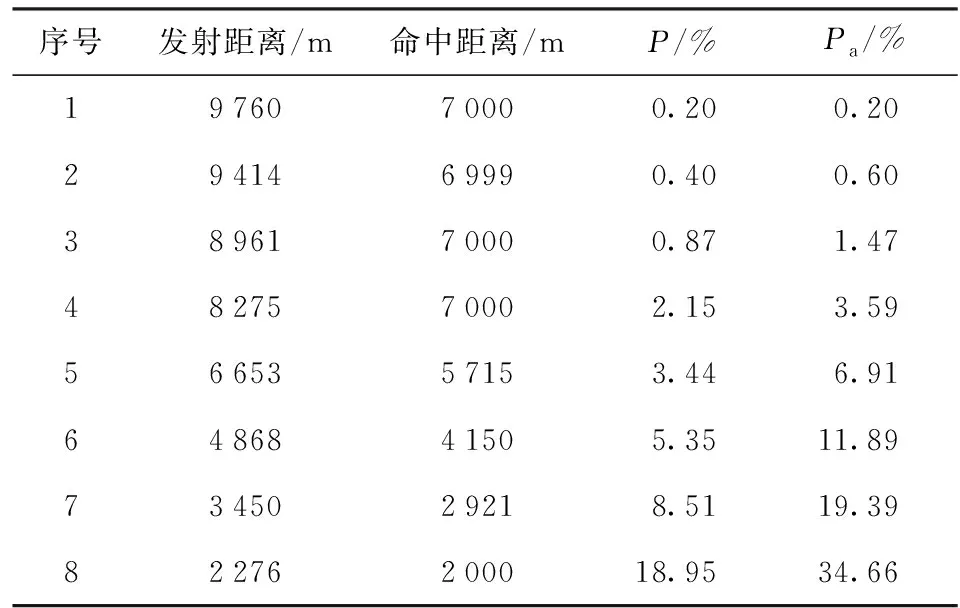
表3 Lmin=2 000 m、Ld=5 000 m、平衡射击策略下目标命中参数

5 结论

基于电磁轨道炮出炮口弹丸初速可调的特点，建立弹丸六自由度外弹道运动方程组以及弹丸对空中目标的单发射击、全航路连续射击的命中概率模型，分析了视距内弹丸初速对空中目标命中概率的影响，并据此提出一种由近及远、有效射程内单发命中概率最大、射击远界上多发同时弹着的全航路平衡射击策略方法。通过仿真计算，得到主要结论如下：

1) 在单发射击下，当弹丸初速相同，目标距离越近，命中概率越大；当目标距离相同，弹丸初速越大，命中概率越大。

2) 在全航路射击区间连续射击下，全航路累积命中概率随着弹丸初速增大，整体上呈先增大、后减小趋势，局部受射击发数减小出现阶跃下降，且射击区间越小，该现象越明显。

3) 由近及远、有效射程内单发命中概率最大、射击远界上多发同时弹着的全航路平衡射击策略，可兼顾目标命中概率和打击成本，以较小的打击成本下获得较优的作战效能。

参考文献(References)

[1] 付彩越. 美国海军新概念武器现状和发展[J]. 舰船科学与技术, 2017, 39(2): 151-154.

FU C Y. US Navy new concept weapon status and development trend[J]. Ship Science and Technology, 2017, 39(2): 151-154. (in Chinese)

[2] MCNAB I R, FISH S, STEFANI F. Parameters for an electromagnetic naval railgun[J]. IEEE Transactions on Magnetics, 2015, 37(1): 223-228.

[3] 张亚舟,李贞晓,田慧,等. 基于反向开关晶体管的脉冲电源在电磁发射中的应用[J]. 兵工学报, 2017, 38(4): 658-663.

ZHANG Y Z, LI Z X, TIAN H, et al. Application of pulse power supply with RSD switch in electromagnetic launch[J]. Acta Armamentarii, 2017, 38(4): 658-663. (in Chinese)

[4] 谢黎焱, 廖瑞, 王雪琴. 信息化条件下单炮多发同时弹着研究[J]. 指挥控制与仿真, 2009, 31(4): 30-32,36.

XIE L Y, LIAO R, WANG X Q. Study on single cannon multiple round time-on-target under informationizated condition[J]. Command Control & Simulation, 2009, 31(4): 30-32,36. (in Chinese)

[5] 吴威,卢发兴,许俊飞, 等. 初速可控舰炮制导炮弹对海射击多发同时弹着技术研究[J]. 电光与控制, 2019, 26(9): 79-83.

WU W, LU F X, XU J F, et al. On MRSI technique of guided projectiles of controllable muzzle velocity shipborne gun for sea target shooting[J]. Electronics Optics & Control, 2019, 26(9): 79-83. (in Chinese)

[6] 卢发兴,贾正荣,吴玲. 舰炮初速对命中点预测误差影响分析[J]. 海军工程大学学报, 2016, 28(3): 21-25.

LU F X, JIA Z R, WU L. Accuracy analysis of measurement noise whitening in target tracking[J]. Journal of Naval University of Engineering, 2016, 28(3): 21-25. (in Chinese)

[7] 许俊飞,卢发兴,王航宇, 等. 初速可调下的新型舰炮对海作战能力需求生成[J]. 北京理工大学学报, 2019， 39(2): 155-161.

XU J F, LU F X, WANG H Y, et al. Anti-sea combat capability requirement generation of new naval gun with adjustable muzzle velocity[J]. Transactions of Beijing Institute of Technology, 2019, 39(2): 155-161. (in Chinese)

[8] 吴威,吴玲,卢发兴. 基于最大命中概率的新型舰炮对海射击火控解算技术[J]. 电光与控制, 2019， 26(3): 44-48.

WU W, WU L, LU F X. Maximum hitting probability based fire control calculation for new shipboard gun against sea target[J]. Electronics Optics & Control, 2019, 26(3): 44-48. (in Chinese)

[9] 吴威,吴玲,卢发兴. 初速可控舰炮对海上目标命中概率的影响[J]. 火力与指挥控制, 2019, 44(2): 175-180.

WU W, WU L, LU F X. Influence of controllable muzzle velocity of shipborne gun on hitting probability of sea target[J]. Fire Control & Command Control, 2019, 44(2): 175-180. (in Chinese)

[10] GALLANT J, VANCAEYZEELE T, LAUWENS B, et al. Design considerations for an electromagnetic railgun firing intelligent bursts to be used against antiship missiles[J]. IEEE Transactions on Plasma Science, 2015, 43(5):1179-1184.

[11] 陈材,石全,尤志锋,等. 基于功能损伤的装备有效毁伤幅员仿真方法研究[J]. 兵工学报, 2020, 41(1):1-12.

CHEN C, SHI Q, YOU Z F, et al. Research on simulation method of effective damage area of equipment based on functional damage[J]. Acta Armamentarii, 2020, 41(1):1-12. (in Chinese)

[12] 王航宇,卢发兴,许俊飞,等. 舰载电磁轨道炮作战使用问题的思考[J]. 海军工程大学学报. 2016, 28(3): 1-6.

WANG H Y, LU F X, XU J F, et al. Application of shipborne electromagnetic rail gun in operation[J]. Journal of Naval University of Engineering, 2016, 28(3): 1-6. (in Chinese)

[13] 邢昌风,李敏勇,吴玲. 舰炮武器系统效能分析[M]. 北京: 国防工业出版社, 2008.

XING C F, LI M H, WU L. Effectiveness analysis of shipborne weapon system[M]. Beijing: National Defense Industry Press, 2008. (in Chinese)

[14] KESHMIRI S, MIRMIRANI M, COLGREN R D. Six-DOF mo-deling and simulation of a generic hypersonic vehicle for conceptual design studies[C]∥Proceedings of AIAA Modeling and Simulation Technologies Conference and Exhibit. Providence, RI, US: AIAA, 2004.

[15] KESHMIRI S, COLGREN R D, MIRMIRANI M. Development of an aerodynamic database for a generic hypersonic air vehicle[C]∥Proceedings of AIAA Guidance, Navigation, and Control conference and Exhibit. San Francisco, CA，US: AIAA, 2005.

[16] 尚晓兵. 电磁轨道炮外弹道射击精度分析与评估技术研究[D]. 哈尔滨：哈尔滨工业大学, 2015.

SHANG X B. Research on firing accuracy analysis and evaluation techniques of electromagnetic rail gun exterior ballistic[D]. Harbin: Harbin Institute of Technology, 2015. (in Chinese)

[17] 钱杏芳,林瑞雄,赵亚男. 导弹飞行力学[M]. 北京: 北京理工大学出版社, 2012.

QIAN X F, LIN R X, ZHAO Y N. Missile flight mechanics[M]. Beijing: Beijing Institute of Technology Press, 2012. (in Chinese)