二维浮体在聚焦波浪作用下的高频共振响应研究

朱显玲,吴英友,齐江辉

(1.武汉船舶职业技术学院 船舶与海洋工程学院, 武汉 430050) (2.广东海洋大学 海洋工程学院, 湛江 524088) (3.武汉第二船舶设计研究所 海洋核动力平台研究室, 武汉 430064)

海洋结构物的剧烈横摇运动是导致船舶或平台倾覆的主要原因,因此相对于其它五个自由度的运动来说横摇运动更加受到科研工作者的关注．驳船在进行货物装卸或特种作业时,对于船体的横摇运动有较高的要求．然而当遭遇波浪频率与驳船的固有频率接近时,船体的横摇运动会较为剧烈,这在线性波浪理论研究中已经被证实[1-2]．

然而在波高增大时,波浪的非线性波浪力变得更加明显,此时高频分量产生的共振现象通常会被忽略．而在不规则波作用下的模型试验和实际运行的平台如张力腿平台和重力式平台中常常可以观测到平台产生瞬态的大幅度共振运动,这种现象被称为“ringing”现象,其通常在平台遭遇较大和较陡的波浪后产生．“ringing”现象是一种近似瞬态的高频共振响应,其频率远高于波浪主导波的频率,其振动幅度可达到包括一阶、二阶波浪力及风动力共同作用达到的幅度,对海上结构物的安全有极大威胁[3]．在高频共振响应研究方面,文献[4]对规则波作用下的二维驳船结构高频共振响应现象进行了研究．文献[5]建立单自由度小尺度桩柱振动模型,在二维完全非线性数值波浪水槽中模拟了海上结构物在极端波浪作用下产生的高频共振响应．聚焦波浪与结构物的耦合作用方面已取得较多研究成果．在试验研究方面,文献[6-7]分别对多向聚焦波浪的影响以及多向聚焦破碎波浪的特性进行了试验研究;文献[8]等研究了极限波浪对圆柱的作用力,并与同尺度的五阶Stokes波进行了对比．在数值计算方面,文献[9]在数值波浪水槽中模拟二维聚焦波浪,并分析了不同聚焦波浪参数对圆柱波浪涌高及波浪力的影响;文献[10]通过数值模拟的方法对极限波浪与结构物的作用进行了研究．通常聚焦波浪与结构物的耦合作用方面均重点关注结构物的运动响应及波浪爬高,而研究表明,高频波浪载荷更容易使浮体产生ringing现象,且当浮体固有频率为波浪主频的3～5倍时最易诱导产生ringing．而聚焦波浪中的波浪分量高倍频率接近浮体的固有频率时,浮体也会出现ringing现象．对于聚焦波浪诱导结构物产生ringing现象的机理及聚焦波浪参数对聚焦波浪现象的影响则鲜有相关研究．文中建立完全非线性数值波浪水槽对聚焦波浪的船舶特性进行数值模拟,并进一步探讨聚焦波浪作用下结构物发生ringing现象的机理及规律,为海洋工程结构物的设计提供指导．

波浪与结构物的非线性相互作用一直是水动力研究的热门,各国的学者已经做了较多的有价值的研究工作[11-15]．根据势流理论及高阶边界元方法,建立了二维驳船结构物与波浪的完全非线性相互作用数值波浪水槽模型．聚焦波浪利用数值水槽的造波板按JONSWAP谱分布形式产生,为了消除由于物体产生的二次反射波浪,在入射边界附近布置人工阻尼层用于消波[13]．求解波浪载荷及运动时,采用间接求解法引入一个虚拟函数,从而可以在每一步直接求解波浪载荷及物体运动而不需要多次迭代．采用四阶Runge-Kutta法实现自由面及瞬时物体湿表面的更新[16]．为验证所采用数值模型的准确性,对数值水槽中聚焦波浪的传播规律与理论解和试验结果进行了对比验证．同时研究了聚焦波浪与浮体的相互作用．研究重点为高频波浪力诱导下的浮体高频共振响应,因此聚焦波浪的主频三倍频率设定为浮体横摇的固有频率,给出了聚焦波幅和频率对ringing现象的影响．

1 数学模型和数值求解

1.1 流场定义和坐标系

图1为浮体与波浪相互作用的坐标系定义和计算域定义．其中,SF为瞬时自由水面边界,SB为瞬时物面边界,SD为水底边界,d为水深．为准确描述物体的运动,共设置两组坐标系描述物体的运动．其中,oxyz坐标系为固定的大地坐标系,坐标原点为静水面处;o′x′y′z′是固定在物体上的随体坐标系,在初始时刻坐标系原点与大地坐标系原点重合．物体的质心和转动中心在大地坐标系下的坐标分别为Xc=(xc,zc)和X0=(x0,z0),在随体坐标系中的位置分别为X′c和X′0．

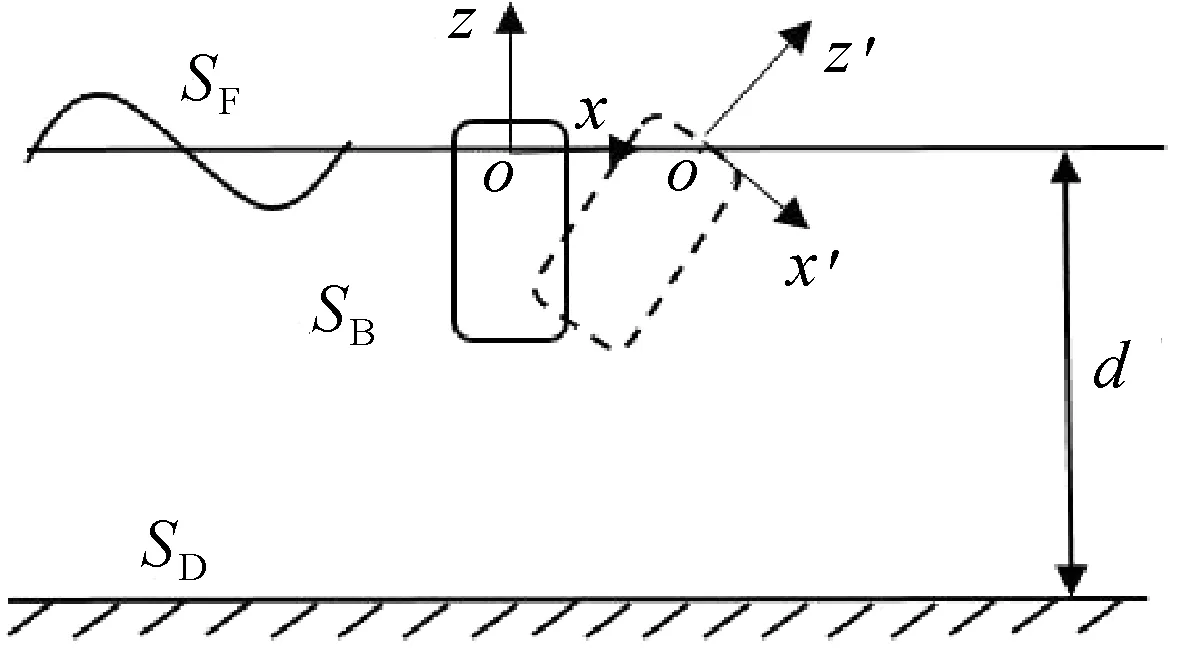
图1 坐标系和计算域定义Fig.1 Definition of coordinate system andcomputation domain

数值模拟的研究物体为二维驳船结构,物体的运动有横荡(sway)、垂荡(heave)和横摇(roll)．从向量角度,物体的运动可以表示为ζ=(ζ1,ζ2,ζ3)．由坐标转换可以得到空间中任一点在两组坐标系下的坐标关系为[17]：

(1)

式中:

(2)

1.2 初边值问题

势流理论假设流体无旋、无粘且不可压缩,同时速度势满足拉普拉斯方程．在瞬时自由水面SF满足非线性自由面条件,在瞬时物面SB和水底边界SD等固体边界满足不可穿透壁面条件．上述边界条件与初始条件一起就构成了关于速度势的初边值问题[14]：

在R内 (3)

在SF上 (4)

在SF上 (5)

在SB上 (6)

在SD上 (7)

式中：rb=(X-X0)为位置矢量；U为物体的平动速度；Ω为物体的转动速度．入射边界为造波板边界,通过给定造波板运动给出造波板上速度势的法向导数．

1.3 人工阻尼层消波

为防止波浪在出流边界反射,在水槽右端布置了人工阻尼层进行消波．而波浪在经过物体时,有可能会形成反射波浪,这会影响模拟结果．因此,同时在入射边界附近布置特殊的阻尼层,增加阻尼项后的自由面条件可写为[13]:

(8)

(9)

其中:

(10)

式中：x1为左端阻尼层在水槽中的截止位置；η*和φ*分别为流场中无结构物时的波面高度和速度势.在计算聚焦波浪与浮体相互作用前,计算相同工况下无浮体时聚焦波浪的传播从而得到η*和φ*．α0为阻尼系数,β0为岸滩宽度系数,取α0=1.0,β0=1.0,λ为特征波长[18]．

在整个流域内应用格林第二定理,上述初边值问题可以转换成边界积分方程．为保证数值结果的精度,数值离散方法采用高阶边界元法,同时利用二次形状函数插值保证各单元内物理量的连续性[12]．

由于物体的运动和造波板的运动使得计算域边界随时变化,因此在每一时间步均进行网格重新划分,这样可以避免网格发生变形而导致数值不稳定,进行网格重新划分后的新网格及节点的物理量可以通过插值进行更新．

2 波浪力和运动求解

作用在物体上的波浪力F={f1,f2}和力矩M={f3}可通过压强在瞬时物体湿表面SB上积分得到:

i=1,2,3 (11)

方法的难点在于速度势的时间导数∂φ/∂t的求解,通过数值差分得到速度势时间导数的方法不够精确,同时在浮体运动幅度较大时该方法便不再适用．解决上述问题的一个有效方法是Wu&Eatock Taylor提出的间接法解耦求解物体运动和波浪力[16]．引入虚拟函数ψi(i=1,2,3),其在计算域中满足拉普拉斯方程,在自由面上满足ψi=0,在物体表面和造波边界满足∂ψi/∂n=ni,在其他边界上满足ψi=0．物体的运动方程可以写为:

(12)

(13)

(14)

式中：mi,j为质量矩阵；Fe=[fe1,fe2,fe3]T为关于物体质心的外力和力矩；SN为固体边界之和；fei为作用在结构物上的外力．上述方法中,物体的加速度在求解物体速度势之后可以直接得到,从而将物体运动和物体受力解耦求解．

3 数值结果

3.1 聚焦波浪的传播

基于线性波浪理论,在水槽某一位置x=xb产生聚焦波浪的造波机信号为:

(15)

式中：T(fi)为造波机传递函数, 其中N为组成波的个数；ai为组成波的波幅;ki为组成波波数;xb和tb分别为假定聚焦位置和聚焦时刻．

通过模拟聚焦波浪的传播特性对上述数值模型的准确性进行验证．选取Baldock[19]试验中的Case D作为模拟工况．选择3种不同的波高进行模拟,其中各成分波周期范围为0.8～1.2 s,每组聚焦波包含29个组成波,各组成波波幅相同并按周期范围等间距分布．计算域长度为12λmin,深度为0.4 m,计算域消波区长度为1.94 m．造波边界与设定聚焦位置距离为xf=8.0 m,设定聚焦时刻为tf=16.0 s．由于聚焦波假定为各组成波的线性叠加,这就忽略了各组成波之间的非线性相互作用导致的实际聚焦位置和聚焦时刻与设定值有一定差异．实际的聚焦位置和聚焦时刻定义为xd和td,通过在设定聚焦时刻附近输出每个时刻的波面形状,其中波高值最大的即视作实际聚焦波面位置,对应的聚焦时刻则为实际聚焦时刻．通过收敛性分析,计算中网格节点间距设为Δx=λmin/40,时间步长设定为Δt=Tmin/60．

图2为3种不同输入波幅A=0.022,0.038,0.055 m时实际聚焦位置处的波面时间历程曲线，η为计算得到的波辐．图中也给出了Baldock的试验值和线性以及二阶理论解．从计算结果与试验值等的对比来看,数值结果与试验值吻合良好,可以验证所采用数值模型的准确性．同时可以看到,在A=0.022 m时数值结果与线性和二阶理论解之间的差异最小,但随着波幅的增大这种差异也会变大,同时随着波幅的增大聚焦波的波峰更大且更陡,波谷则更加平缓,这是由于波幅的增大使得各组成波之间的非线性相互作用增强．

图2 聚焦位置处波面升高时间历程曲线Fig.2 Time history of wave elevation at exact focuspoint with different wave amplitudes

3.2 浮体的高频共振响应

驳船结构物与波浪相互作用数值水池模型如图3．选择与文献[2]中相同的几何模型,坐标系如图3,其中物体的质心与转动中心重合,坐标为(0,-0.115),弹簧系数k=197.58 N/m,阻尼系数D11=c=19.8 N/(m·s-1),物体吃水B=0.25 m,物体宽度rd=0.5 m,物体质量m=125 kg,转动惯量I=4.05 kg·m2,水池深度h=λmax．

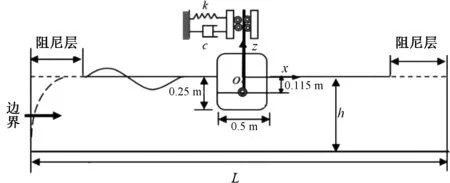
图3 弹簧系泊驳船结构浮体及数值水池示意Fig.3 Sketch of a floating barge in numerical wavetank with spring type mooring

浮体的固有频率根据频域无阻尼自由运动方程得到:

(16)

式中：mi,j与公式(12)中定义相同；am(i,j),Ki,j,Ci,j分别为附加质量系数、刚度系数和恢复力系数．刚度系数K11=k=197.58 N/m,K22=K33=0．恢复力系数C11=0,C22=5.016×103N·m-1，C33=91.965 N·m·rad-1．

驳船结构的附加质量am(i,j)为频率的函数,由线性理论可知,辐射力可以分解为附加质量力和阻尼力．通过给定驳船结构物一个强迫周期性运动,通过对物体受到的周期性辐射力进行傅里叶分析可以得到附加质量．而浮体的固有周期可以通过迭代得到,浮体3个方向的固有周期如表1，ωn，fn分别为浮体的固有圆频率、频率．

表1 浮体各方向固有频率Table 1 Natural frequencies of the floating barge

当入射波浪的三倍频率接近物体的固有频率时,物体很容易发生ringing现象．为了研究浮体在横摇方向的ringing现象,设定入射波浪的谱峰频率fp=fn/3=0.23 Hz．数值水槽长度L=8λp，其中λp为谱峰频率对应的波长,消波区域长度为组成波中最大的波长长度．造波板距指定的聚焦位置的距离xt=113.0 m,指定的聚焦时刻tf=25Tp．如同前文所述,实际聚焦位置和聚焦时刻是在数值水槽中没有浮体时计算得到．数值模拟选取波浪参数及聚焦位置等如表2，rd为浮体宽度，xd为实际聚焦位置．

表2 波浪参数及聚焦位置Table 2 Wave parameters and the focus position

进行数值收敛性分析,选取两种网格尺度和两种时间步长分别进行收敛性分析，如图4．Mesh a网格在浮体附近尺寸为Δx=λp/120=0.125,在远离浮体后网格增长率为1.1．在浮体表面垂向和水平方向网格数量分别设置为8和4,入射边界表面和出流面网格设置为60．Mesh b的网格尺寸为Mesh a的一半．对于两种网格尺寸时间步长均设定为Δt=Tp/60．为对时间步长的收敛性作分析,分别取Δt=Tp/60和Δt=Tp/120,两种情况下的网格均取Mesh a．图4中显示不同网格和不同时间步长下浮体的横摇运动时历曲线．可以看出两种网格尺寸以及两种时间步长下浮体运动曲线几乎吻合,因此后续计算中网格尺度及时间步长分别选定Mesh a和Δt=Tp/60，ξ3为浮体位移．

图4 浮体横摇运动收敛性分析(A/rd=0.8，fp=fn/3)Fig.4 Convergence study with mesh and time step formotion responds with A/rd=0.8 at fp=fn/3

探索浮体高频共振响应现象的特征．图5为入射波幅A/rd=1.6时浮体横摇运动的时间历程曲线．图6给出了在没有浮体时不同时刻数值水槽中的波形．从图6(b)中可以看出在(t-tf)>15 s时,聚焦波浪已经越过浮体,此时从图中仍可以看到浮体横摇方向有较大的运动幅度．实际上,在入射波谱峰频率的3倍频率设定为浮体横摇方向的固有频率时,聚焦波浪中各组成波之间的非线性相互作用就变得不可忽略．由于这种非线性作用,在聚焦波浪越过浮体之后,浮体仍会以高频振动的方式持续运动几个周期,这属于典型的ringing现象特征．

图6 数值水槽不同时刻聚焦波波形Fig.6 Wave profile along the waveflume at different times

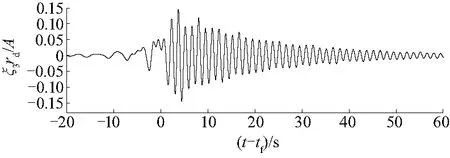
图5 浮体横摇运动时历曲线(fp=fn/3, A/rd=1.6)Fig.5 Roll motions of the barge with (fp=fn/3, A/rd=1.6)

为进一步研究高频共振响应的特性,计算分析了入射波浪频率对高频共振响应的影响,计算中选取入射波幅为A/rd=1.6．图7分别给出了fp=0.18、0.23、0.28 Hz时浮体的横摇运动响应．可以看出,在fp=fn/3=0.23 Hz时浮体的高频共振响应最为明显,而在入射波频小于fn/3时,高频共振响应现象有明显的减弱;而在入射波频大于fn/3时,高频共振响应仍旧非常显著．这表明导致浮体发生高频共振响应的入射波浪频率范围较大．

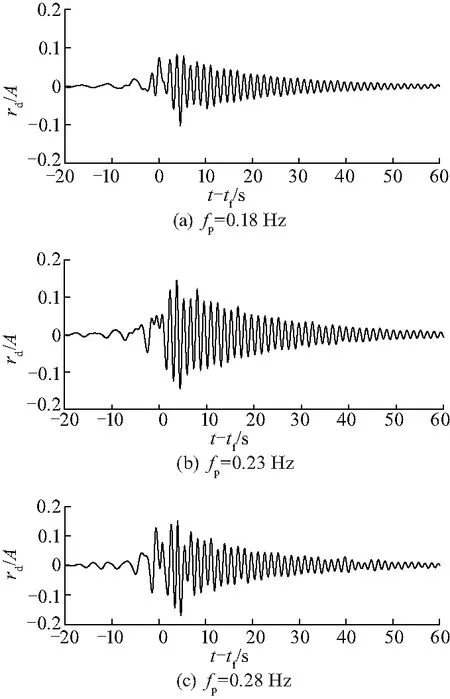
图7 不同谱峰频率时浮体横摇运动时历曲线(A/rd=1.6,fp=fn/3)Fig.7 Roll motions of barge with A/rd=0.8 atdifferent typical wave frequencies

图8为不同谱峰频率时物体横摇运动的响应谱对比(15s≤(t-tf)≤60 s)．从图中可以看出,在共振谱峰频率附近取谱峰频率(fp2=0.225 Hz,fp4=0.235 Hz)时,高频运动非常明显,总体来看计算结果与共振谱峰频率(fp3=0.23 Hz)时的计算结果相差不大．同时可以看出,不同谱峰频率下物体横摇运动谱中最大幅值均出现在f=3fp3=0.690 7 Hz时．但在远离共振谱峰频率取谱峰频率(fp1=0.18 Hz,fp5=0.28 Hz)时,高频运动的幅值相对于fp3=0.23 Hz时分别减少35%和42%．此外,浮体的固有频率是依据频域无阻尼线性理论方程求解得到,而由于波浪的非线性影响,浮体高频共振响应最明显时的频率可能要比浮体的固有频率大．所有上述表述均表明在海洋工程设计中避免入射波浪的三倍频率接近浮体固有频率的重要性,同时也强调了该类问题中波浪非线性特性所起的重要作用．

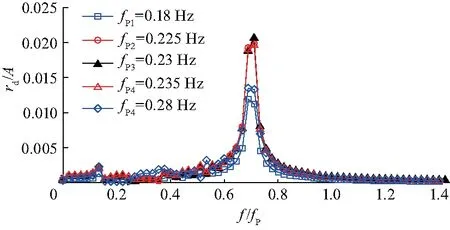
图8 不同谱峰频率下物体横摇运动响应谱对比(15 s≤(t-tf)≤60 s)Fig.8 Comparison of response spectra of rolling motionat different typical wave frequenics

4 结论

(1) 建立了二维完全非线性数值波浪水槽模型,基于该数值模型,研究了完全非线性聚焦波浪在数值水槽中的传播特性,数值计算结果与试验值对比良好,验证了所建立数值模型的准确性．

(2) 当入射波浪主频的三倍频等于物体横摇方向固有频率时,物体横摇运动发生明显的ringing现象,在聚焦波浪经过浮体之后的几个周期内浮体仍存在较大程度的ringing现象且ringing现象与入射波幅和谱峰频率密切相关．

(3) 入射波浪谱峰频率三倍频接近浮体固有频率时,高频共振响应幅值与谱峰频率三倍频等于固有频率时相差不大;谱峰频率三倍频远离浮体固有频率时(分别为固有频率的0.8倍和1.2倍),高频共振响应幅值与谱峰频率三倍频等于固有频率时分别减小35%和42%．

(4) 导致浮体发生ringing现象的入射波频率范围较大,同时由于波浪的非线性特性使得实际ringing现象最显著时对应谱峰频率的三倍频要比浮体的固有频率略大,上述情况均表明了在海洋结构物设计和运行过程中尽量避免入射波浪的三倍频接近浮体的固有频率的重要性．

参考文献(References)

[1] CHEN L F,SUN L, ZANG J, et al. Numerical study of roll motion of a 2-D floating structure in viscous flow[J]. Journal of Hydrodynamic, 2016, 28(4), 544-563.

[2] KOO W, KIM M H. Freely floating-body simulation by a 2D fully nonlinear numerical wave tank[J]. Ocean Engineering, 2004, 31(16):2011-2046.

[3] 于定勇, 徐德伦, 李瑞杰. 海上结构物的Ringing现象 [J]. 海岸工程, 1997, 16(3): 6-11.

[4] 齐江辉,周斌珍,郑亚雄. 二维驳船结构在规则波作用下的高频共振响应研究[J]. 江苏科技大学学报(自然科学版), 2019, 33(2): 9-13. DOI:10.11917/j.issn.1673-4807.2019.02.002.

QI Jianghui, ZHOU Binzhen, ZHENG Yaxiong. Research of the high frequency resonance of a two dimensionalbarge induced by regular waves[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2019, 33(2): 9-13. DOI:10.11917/j.issn.1673-4807.2019.02.002.(in Chinese)

[5] 庞红犁. 极端波浪作用下海上结构物高频共振响应的数值模拟研究 [D]. 天津: 天津大学,2003.

[6] 李金宣,柳淑学,孙一艳,等. 分布方向对三维聚焦波浪波面特性影响研究[J]. 海洋工程,2008,26(2):26-33.

LI Jinxuan, LIU Shuxue, SUN Yiyan, et al. Study on effect of directionality on 3D focusing wave characteristics[J]. Ocean Engineering, 2008, 26(2):26-33.

[7] 柳淑学,李金宣,HONH K. 多向聚焦波破碎的实验研究[J]. 水动力学研究与进展,2007,22(3):293-304.

LIU Shuxue, LI Jinxuan, HONG K. Experimental study on multi-directional focused wave breaking in wave basin[J]. Journal of Hydrodynamics,2007,22(3):293-304.(in Chinese)

[8] KIM N, KIM C H. Investigation of a dynamic property of drauper freak wave[J]. International Journal of Offshore and Polar Engineering, 2003, 13(1): 38-41.

[9] 孙一艳,柳淑学,臧军,等. 聚焦波浪对直立圆柱的作用[J]. 大连海事大学学报,2008, 34(1): 5-9.

SUN Yiyan, LIU Shuxue, ZANG Jun, et al. Experimental study of focused wave on a vertical circular cylinder[J]. Journal of Dalian Maritime University, 2008, 34(1): 5-9.(in Chinese)

[10] CORTE C, GRULLI S T. Numerical modeling of extreme wave slamming on cylindrical offshore support structures[C]∥16thInternational Offshore and Polar Engineering Conference, San Francisco, USA:[s.n.], 2006:394-401.

[11] KIM C H, RANDALL R E, KRAFFT M J, et al. Experimental study of kinematics of large transient wave in 2-D wave tank [C]∥Offshore Technology Conference, Houston, USA:[s.n.], 1990:195-202.

[12] FENTON J D. The numerical solution of steady water wave problems [J]. Computers & Geosciences,1988(14): 357-368.

[13] KOO W, KIM M H. Freely floating-body simulation by a 2D fully nonlinear numerical wave tank [J]. Ocean Engineering, 2004, 31(16):2011-2046.

[14] ZHOU B Z, NING D Z, TENG B,et al. Numerical investigation of wave radiation by a vertical cylinder using a fully nonlinear HOBEM [J]. Ocean Engineering, 2013:1-13.

[15] 刘源, 李进, 段晔鑫, 等. 波浪与多柱结构物的非线性相互作用[J]. 江苏科技大学学报(自然科学版), 2016,30(5):424-429.DOI:10.3969/j.issn.1673-4807.2016.05.003.

LIU Yuan, LI Jin, DUAN Yexin, et al. Reaearcn on nonlinear interaction of muti-structures and wave[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2016, 30(5):424-429. DOI:10.3969/j.issn.1673-4807.2016.05.003.(in Chinese)

[16] WU G X, EATOCK T R. The coupled finite element and boundary element analysis of nonlinear interactions between waves and bodies [J]. Ocean Engineering, 2003, 30(3): 387-400.

[17] 刘应中,缪国平. 船舶在波浪上的运动理论[M]. 上海：上海交通大学,1987.

[18] MARUO H. On the increase of the resistance of a ship in rough seas (I) [J]. Journal of Zosen Kiokai, 1957(19):235-237.

[19] BALDOCK T E, SWAN C, TYLOR P H. A laboratory study of nonlinear surface waves on water [J]. Philos Trans R Soc Long Ser A, 1996(354):649-76.