自适应Frank-Wolfe算法及其在矩阵填充上的应用

汪丽琴，喻高航，张亮亮

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

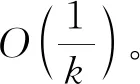
1 低秩矩阵填充模型

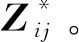
(1)

式中，δ表示对Z的秩的假设置信度，通常取某个正整数。模型(1)综合考虑了无噪音和有噪音的情况。由于秩函数是非凸且非连续的，计算模型(1)十分困难。Fazel[5]证明核范数在单元球上是秩的最紧凸松弛替代，随后，Candès和Recht[6]提出使用矩阵核范数代替秩来解矩阵填充问题，得到模型：

(2)

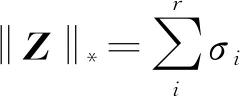
2 Frank-Wolfe算法

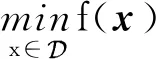
(3)

给出Frank-Wolfe算法。

算法1 用于解决问题(3)的标准Frank-Wolfe算法输入:x0∈,最大迭代步数K 当k=1,2,…,K时,(1)计算sk-1=argmins∈(2)搜索方向dfw=sk-1-xk-1(3)更新xk=xk-1+γdfw,其中γ∈[0,1]输出:xK

针对步骤3中步长的选取，本文使用精确线搜索策略，即γ=argminγ∈[0,1]f(xk+γdfw)。

由于核范数的对偶范数是算子范数，即‖Y‖=max‖X‖*≤1〈X,Y〉，因此最优化问题

minX〈X,Y〉 s.t.‖X‖*≤1

2.1 CGS算法

Lan等[8]使用Nesterov加速方法，提出FW算法的改进算法CGS。

算法2 FW算法的变体CGS算法输入:x0∈,最大迭代步数K 取βk∈R++,γk∈[0,1],和ηk∈R+,k=1,2,…,令y0=x0 当k=1,2,…,K时,(1)计算zk=(1-γk)yk-1+γkxk-1(2)计算xk=CndG f'(zk),xk-1,βk,ηk (3)更新yk=(1-γk)yk-1+γkxk输出:yK 子程序xk=CndG f'(zk),xk-1,βk,ηk 的步骤如下:(1)初始化g=f'(zk),u=xk-1,β=βk,η=ηk(2)令u1=u和t=1(3)令vt为子问题Vg,u,β(ut)maxx∈的最优解(4)如果Vg,u,β(ut)≤η,则令xk=ut,并跳转到步骤7,否则,进入步骤5(5)令ut+1=(1-αt)ut+αtυt,其中αt=min1,<β(u-ut)-g,υt-ut>β‖υt-ut‖2 (6)令t=t+1,并跳转到步骤3(7)返回xk

2.2 In-Face步骤

对于矩阵填充问题，FW算法的一个不足之处在于其中间解决方案的秩通常稳定增长，并在终止时产生一个高秩的解决方案，这对于大规模问题[13]可能在时间和空间成本上非常昂贵。

随后，Freund等[9]提出加In-Face步骤的拓展FW算法IF-(0,∞)，In-Face步骤是远离步骤的推广，远离步骤的具体细节见文献[14-15]。In-Face步骤沿着包含当前迭代的最小面选择最佳下降方向，通过沿着最小面移动到可行域的边界以达到低维面。该算法保持了低秩结构，且不会影响收敛。对于问题(2)，如文献[9]所述，包含点Xk核范数球NN(0,δ)的最小面由下列集合给出：

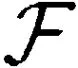
其中，Xk具有秩为r的薄SVDUΣVT，M为满足tr(M)=δ的半正定矩阵。薄SVD表示具有严格正奇异值的SVD，即，如果A=UΣVT是薄SVD且rank(A)=r，则U∈Rm×r，Σ∈Rr×r，V∈Rn×r。

本文考虑文献[9]中描述的由远离策略得到的In-Face步骤，它使用的方向如下：

3 自适应FW算法及其收敛性分析

为了提高FW算法的收敛率并降低迭代过程中的计算成本，本文提出嵌入秩下降步骤的矩阵填充问题的IF-CGS算法。

算法3 IF-CGS算法输入:初始迭代点x0∈,超参数c>0,最大迭代步数K 取βk∈R++,γk∈[0,1],和ηk∈R+,k=1,2,…,令y0=x0 当k=1,2,…,K时,(1)当yk-1在NN(0,δ-c)内部时,计算CGS:zk=(1-γk)yk-1+γkxk-1xk=CndG f'(zk),xk-1,βk,ηk yk=(1-γk)yk-1+γkxk(2)当yk-1在NN(0,δ-c)外部时,计算远离方向满足yk-1+dk∈Aff D(yk-1) 和∇f(yk-1)Tdk<0如果dk不存在,则跳转到步骤1,计算CGS,否则,进入步骤3(3)αstopk=argmaxα{α︰yk-1+αdk∈D(yk-1)}yAk-1yk-1+αstopkdk(4)如果f(yAk-1)≤f(yk-1),则进入步骤5,否则,跳转到步骤1(5)更新yk=yAk-1输出:yK

步骤1进行CGS计算，当秩增长到一定程度时执行步骤2，计算In-Face步骤下的迭代点更新，并在In-Face步骤和CGS步骤进行选择，若In-Face步骤下的目标值小于上一次迭代的目标值，则执行In-Face步骤，否则执行CGS步骤。在加In-Face步骤的CGS算法的框架下，接受任何不增加目标函数值的降秩步骤，允许算法维持较低秩的SVD，并且允许算法跳过不必要的CGS计算。

对{βk}，{γk}和{ηk}提供一种参数设置，得到其收敛性结果。

定理1如果IF-CGS算法中的参数{βk}，{γk}和{ηk}设置如下：

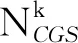
证明当下一个迭代点由步骤1选取，则有

4 数值实验与分析

分别使用FW，IF-(0,∞)，CGS，IF-CGS算法进行数值实验，从数据恢复精度和运行时间进行性能分析。

4.1 合成数据

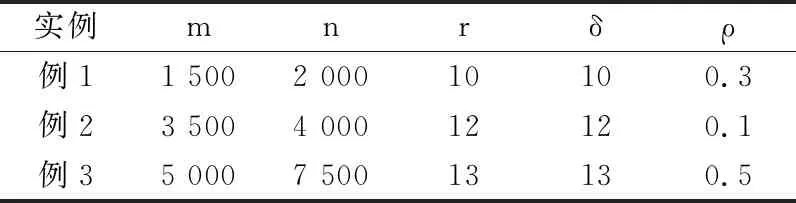
表1 中大型规模合成数据的参数设置

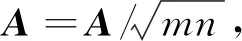
抽取观察数据的50%作为训练集，剩下的50%作测试集，例1运行150 s，例2 运行250 s，例3 运行500 s，超参数c设置为0.5，使用目标值和测试均方根误差(Root Mean Squared Error，RMSE)作为评估标准，用于衡量预测值与真实值之间的偏差，

实验结果如图1和图2所示。

图1 不同算法目标值随运行时间变化的情况

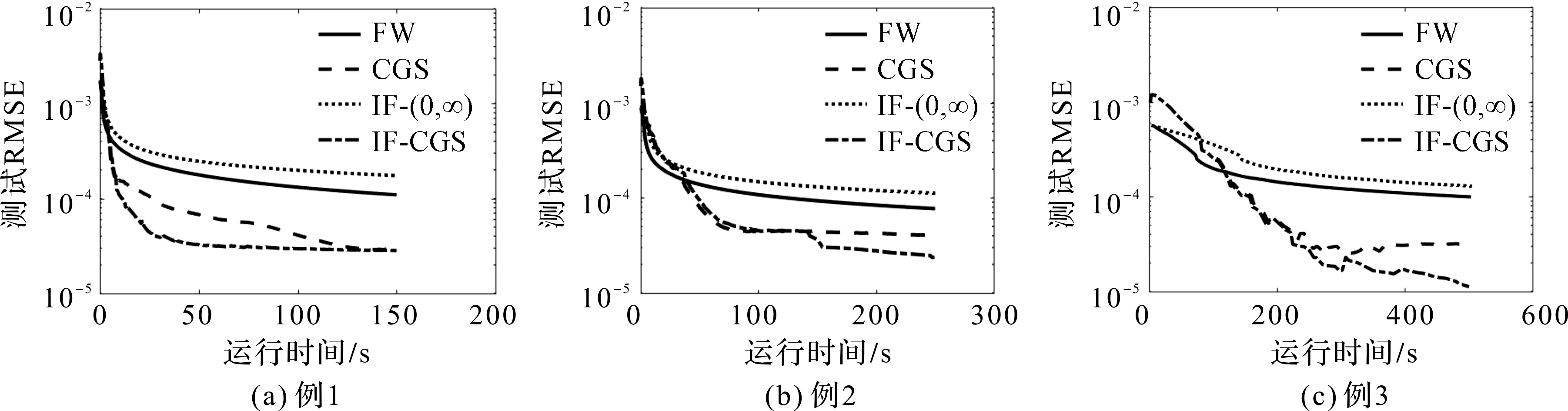
图2 不同算法测试RMSE随运行时间变化的情况

从图1和图2可以看出，IF-CGS算法降低目标值和测试RMSE的速度比其他方法快，解的精度也高于其他方法。在初始迭代阶段，IF-CGS算法迭代点在NN(0,δ-c)内部执行CGS计算，所以IF-CGS算法与CGS算法基本是同步的，当IF-CGS算法迭代点达到NN(0,δ-c)外部时，开始在In-Face步骤与CGS步骤中进行选择，执行In-Face步骤能够减少迭代成本，所以，相比CGS算法，IF-CGS算法的收敛速度更快。

4.2 Movielens-10M数据集

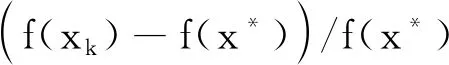
表3 Movielens-10M数据集实验中，不同算法的性能指标

5 结束语

Frank-Wolfe算法的变体CGS算法解矩阵填充问题的一个不足之处在于其中间解的秩通常会稳定增长，并在终止时达到高秩的解。本文针对这个不足，嵌入秩下降步骤，提出求解低秩矩阵填充问题的IF-CGS算法。所提算法在保持线性收敛的同时减少迭代成本，有效解决了大规模的低秩矩阵填充问题。但是，In-Face步骤确定最大可行步长时需要进行多次SVD更新，导致昂贵的中间迭代，针对秩下降步骤的选取问题展开进一步研究是有意义的。