一种提高DTW运算效率的地磁匹配组合导航算法
2021-04-07张东丽尚俊娜保金宏
张东丽,尚俊娜,保金宏
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
0 引 言
近年来,导航定位技术不断发展,组合导航可以弥补单种导航方式的缺陷,综合多种导航方式的优势,受到业界的青睐。常见的导航方式有GPS导航、天文导航、地形匹配导航和地磁导航等,其中地磁导航具有无需信号基站、成本低廉、安全性高等优势,成为具有广泛应用潜力的辅助导航方式[1-2]。基于地磁场的定位技术具有全天时、全地域、无源性、无辐射、低功耗等特点,成为定位领域的研究热点[3]。文献[4]首先利用Wi-Fi得到定位数据,然后根据定位数据确定地磁数据库所需匹配的范围,这一方式使得地磁匹配算法的运算量降低。胡金平等[5]采用改进的序列匹配算法进行语音序列匹配,有效提高了系统的识别率。针对地磁序列匹配导航定位中动态时间规整算法计算时间长、实时性差等问题,本文提出一种基于减少动态时间规整(Dynamic Time Warping,DTW)运算量的地磁匹配算法,通过减少重复计算量来降低算法的复杂度,在保证定位精度的基础上,提高了运行效率。
1 地磁匹配组合导航
1.1 地磁序列匹配组合导航定位原理
地磁定位分为离线阶段、在线阶段。离线阶段包括地磁数据空间对齐和基准位置参考坐标系的建立;在线阶段即地磁序列匹配阶段。序列匹配过程中易发生误匹配问题,因此本文引入高精度惯性导航系统(Inertial Navigation System, INS)为地磁匹配提供空间里程基准服务[6]。
1.2 地磁匹配算法
如果2个序列需要进行相似度比较,常用的方法是DTW匹配算法[7-8]。假设有2条不同的时间序列Q(q1,q2,…,qi,…,qn)和C(c1,c2,…,cj,…,cm),令D(n×m,n≠m),D为累积距离矩阵。D中的元素d(i,j)=(qi-cj)2代表Q中点qi和C中点cj之间的欧式距离,在D中动态规划的思想是从起点d(1,1)到d(n,m)之间找到一条累积距离最小的路径,也就是动态规整的距离[9]。DTW匹配算法执行过程中的路径L在计算距离矩阵时遵循以下原则:
(1)边界性:初始点必须为(1,1),且max(m,n)≤dL≤m+n,dL为路径L的长度。
(2)连续性:路径L中的元素是连续的。
(3)单调性:L经过(i,j)的之前一步只能是(i-1,j),(i,j-1),(i-1,j-1)中的1个点,而点(i,j)选择这3个点中的最小值所对应的点作为前一个点,进而得到累积距离D(i,j)。具体方式如下:
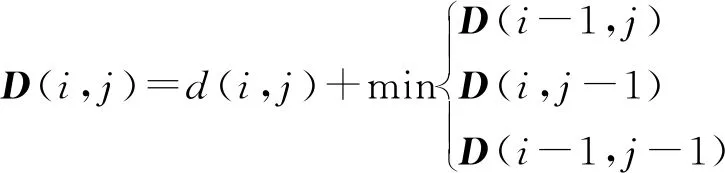
(1)
式中,D(i,j)为累积匹配距离,d(i,j)为2个地磁序列之间的距离。
2 地磁匹配算法的改进
2.1 DTW算法的改进
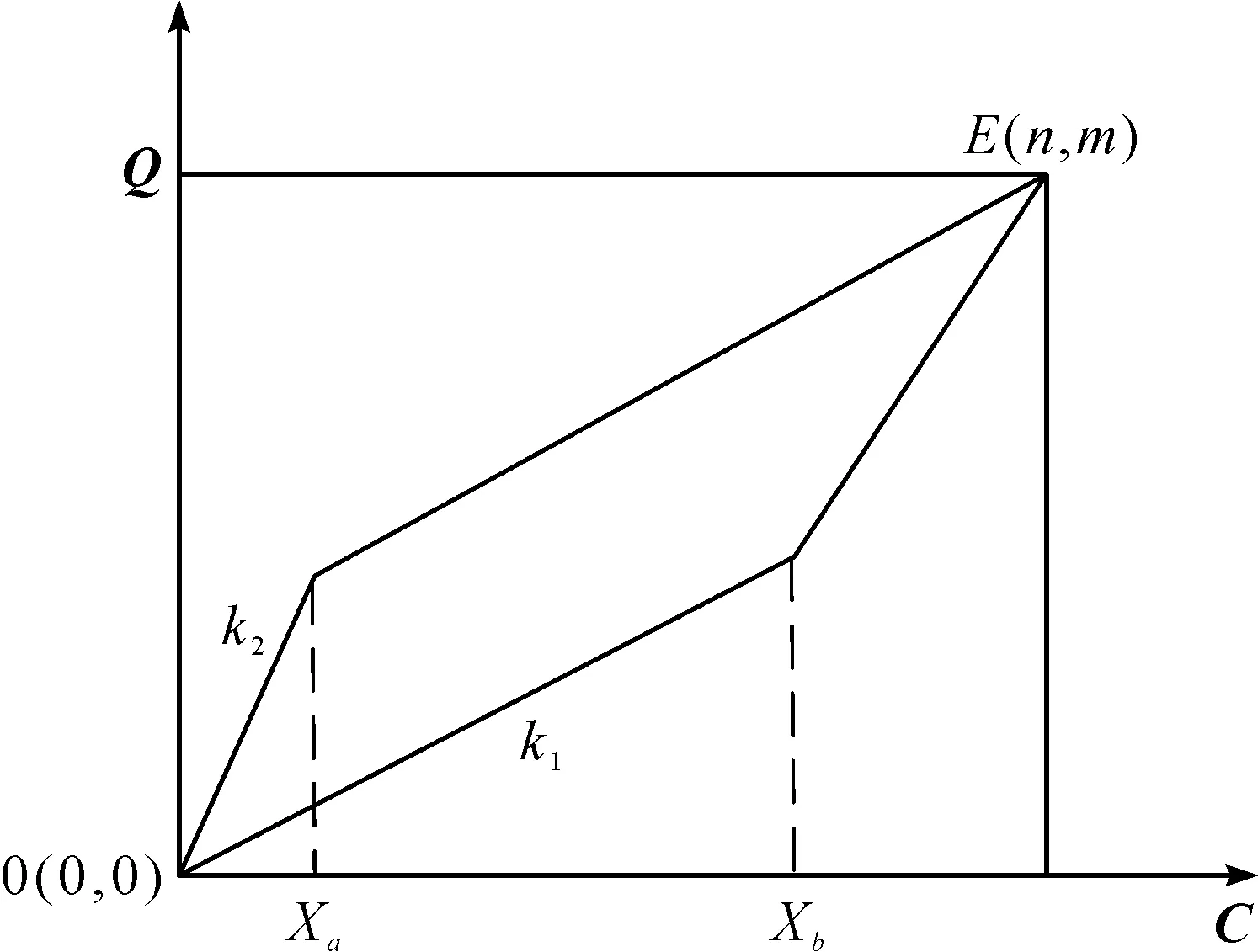
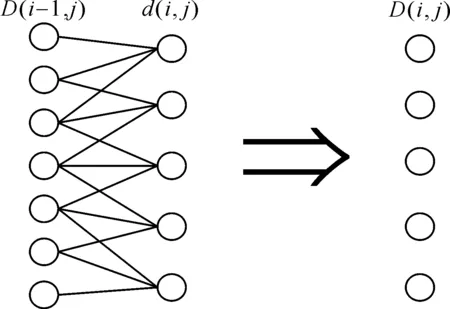
图1 匹配路径约束示意图
根据1.2节的讨论可以看出,DTW算法需要不断按照式(1)去寻找累积矩阵元素(i,j),直到最后1个元素(m,n)。算法每次执行都会从第1个元素到最后1个元素,时间复杂度为o(mn)。当序列长度比较长时,产生更多的多余计算,计算复杂度更大。某些情况下,DTW算法将一个序列上的一点映射到另一条序列上多个点,导致病态规整。因此,如何提高匹配算法的运算速率并避免发生病态规整成为研究的难点和热点。为了解决上述难题,Itakura[10]研究了一种约束窗口,将DTW的路径L控制在一个菱形中,将规整路径控制在对角线周围,每次计算匹配距离矩阵、累积距离矩阵都用不到菱形外的网格点。运用这种全局约束计算每列中的每个点匹配距离时,只用到前一列的3个网格点,不仅减少了计算的次数和存储的数量,还避免了因为搜索范围多导致的病态规整。通常将这个约束窗口的一条边斜率设为1/2,令其为k1。另外一条边的斜率设为2,令其为k2,规整的路线从(1,1)开始到(n,m)结束。匹配路径约束示意图如图1所示。
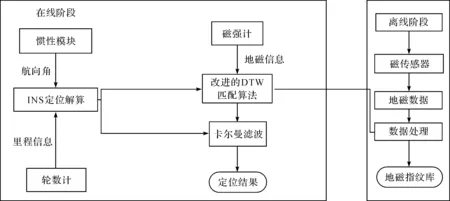
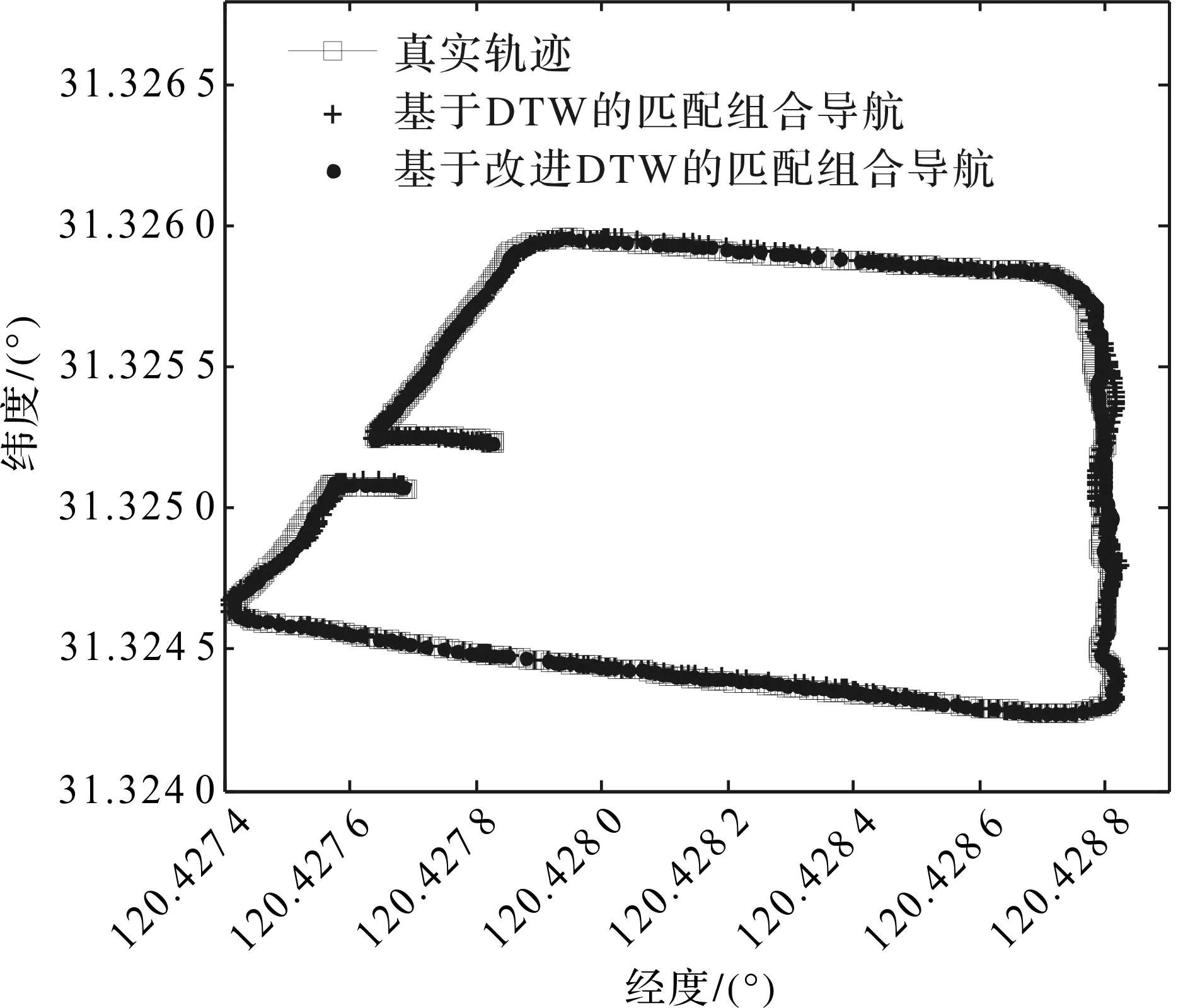
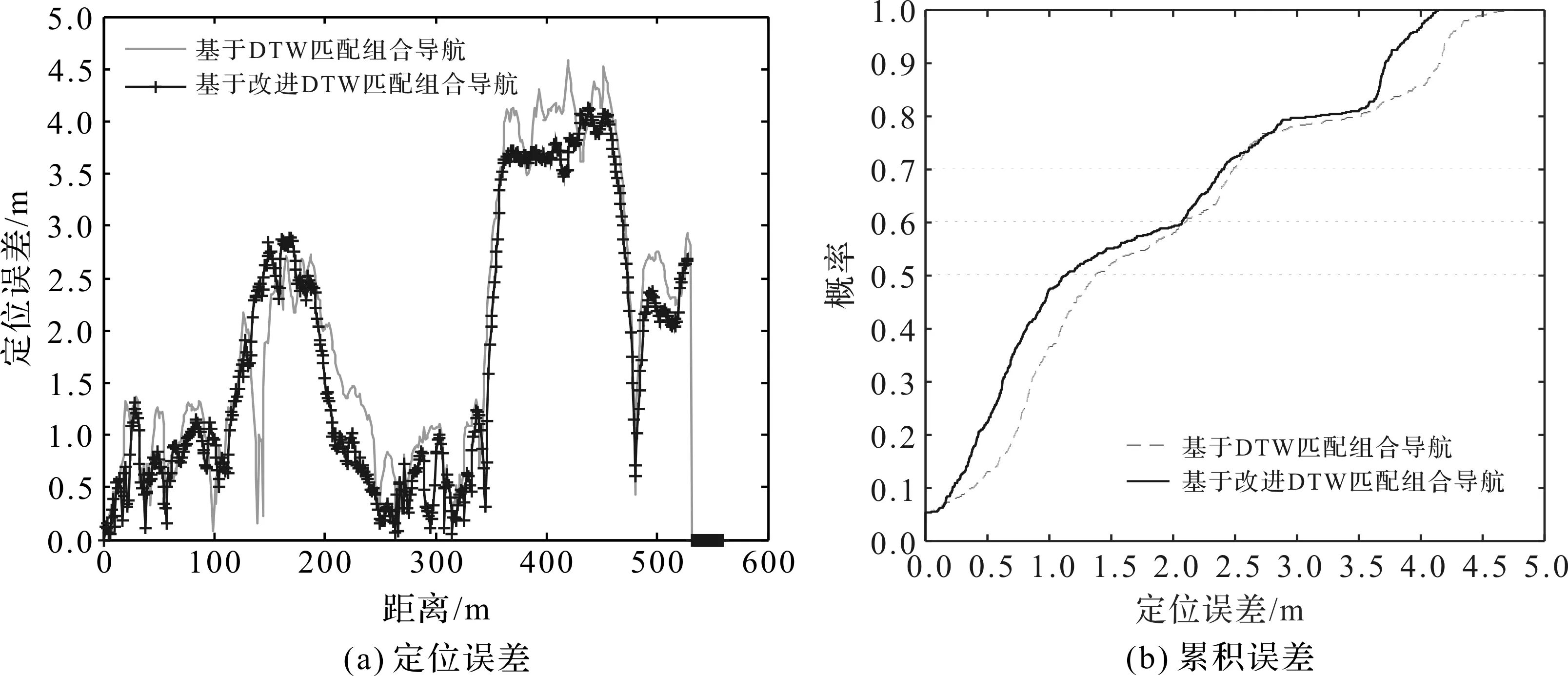
图1中,Xa和Xb表示的是斜率为k1和k2的2条边的不同的交点,C和Q表示待匹配的序列,E(n,m)表示路径规整的终点。当Xa (2) 因为Xa和Xb取最邻近的整数,所以m,n长度限制条件为: (3) 如果都不符合以上情况,说明两段序列相差太多,不能执行动态匹配的规整。 DTW匹配算法需要计算2个序列中每个点之间的距离,加约束窗口后的DTW匹配算法只要计算横坐标与(ymin,ymax)内点之间的距离即可,无需计算与约束窗口外纵坐标点之间的距离。(ymin,ymax)的取值范围如下: (4) (5) 还有一种情况是Xa>Xb,弯折匹配的3段转换为(1,Xb),(Xb+1,Xa),(Xa+1,n)。 加约束窗口后的动态规划过程中,X轴向前滑动一步需要比较的Y轴上的长度与加约束窗口前不同,但是特点是相同的。累积距离为: (6) 图2 累积距离矢量的动态更新图解 横坐标每向右移动一次,就要使用上一列的累计距离D来计算当前列的累计距离。矢量d用来保存当前需要计算的列累计距离,矢量D只保存上一列的累积距离,这样,每计算一列就更新一次D和d,需要保存的内容可以减少很多。最后得到D中的第m个元素即为所求的2个序列之间的匹配距离。累计距离图解过程如图2所示。 本文中的欧氏距离d(i,j)代表2个序列之间的点的真实距离。n维空间的距离计算公式如下: (7) 本文进行动态规划时,欧氏距离的计算和对比采用的是平方值而不是平方根,缩减了每一次计算规划路径的复杂度,最后对输出结果开根号即可得到欧氏距离。 根据2.1节讨论可知,采用改进DTW匹配算法进行匹配定位时,要匹配到具有最小的相似距离的地磁序列。令在线实时测量的地磁序列长度为s,测量结果为Bs=(B1,B2,…,Bs),数据库的地磁序列长度为t(t>s),令Bt=(B1,B2,…,Bt)。在Bs中选取从第1个数据开始到第s个数据结束的片段,再使用改进后的DTW匹配算法将该片段与序列Bs进行对比计算,得到两序列中最短的距离。以此类推,直到计算完所有的序列,再采用2.1节中累计距离矢量更新步骤计算出累计距离D,最后得到D中的第m个元素所对应的位置坐标。 室外地磁匹配组合导航的实现主要分为两部分[11]。第一部分为建立离散地磁数据库,采用GPS482结合磁强计建立离散地磁数据库。第二部分为在线匹配过程,将地磁传感器测量出的数据和数据库中的数据做匹配,本实验使用的匹配算法是改进的DTW匹配算法。同时利用惯导测得的位置信息进行修正,kalman滤波器[12]融合两者定位信息,得到最终结果。具体过程如图3所示。 图3 基于改进DTW算法的地磁匹配组合导航流程图 仿真实验中,首先进行地磁场数据的采集,使用巡航车搭载GPS482模块以及JY901模块实验对应的匹配窗口大小分别为20,40,60,地磁匹配导航定位位置更新时间为1 s,实验参数如表1所示。 表1 实验参数 实验分别采用DTW匹配算法和改进DTW匹配算法解算测试轨迹,定位轨迹如图4所示。将不同匹配算法的地磁匹配组合导航定位轨迹在Google地图上显示,结果如图5所示,不同匹配算法得到轨迹的表示形式与图4相同。 图4 不同匹配算法定位轨迹对比 图5 不同匹配算法在Google地图上的定位轨迹 用在一个位置定位100次来得到一次定位的平均时间,DTW匹配算法和改进的DTW匹配算法的定位时间对比结果如表2所示。 表2 不同算法定位时间平均值 从表2可以看出,在匹配窗口为20,40,60时,改进的DTW匹配算法定位运行时间比传统DTW匹配算法定位效率分别提升了29.2%,41.1%,59.8%。运算效率平均提升了43.37%。 因为匹配窗口一般都是设为总序列的1/30~1/10,实验的地磁数据序列为530,在此范围内匹配序列越长,匹配准确率越高,所以,本实验采用的匹配窗口为60,得到定位误差和累积误差对比结果如图6所示。2种匹配算法组合导航的定位误差对比如表3所示。 图6 不同地磁匹配算法组合导航误差对比 表3 不同匹配算法组合导航误差对比 从图6、表3可以看出,2种匹配算法的平均精度差别不大,改进的DTW匹配算法定位误差比传统DTW匹配算法的平均精度减小了0.22 m。 综合以上分析发现,改进的DTW匹配算法定位性能比传统DTW匹配算法定位性能好,并且耗时少。 针对DTW匹配算法存在病态规整、时间复杂度较高等缺点,本文提出一种改进的DTW匹配算法,在序列匹配过程中添加Itakura约束窗口,减少了算法运算复杂度。在保证定位精度的基础上,提高了运行效率。但是,由于场地及设备的限制,实验环境较为简单,后续将继续改进算法使其在更为复杂环境下快速精确地定位目标。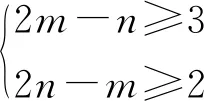
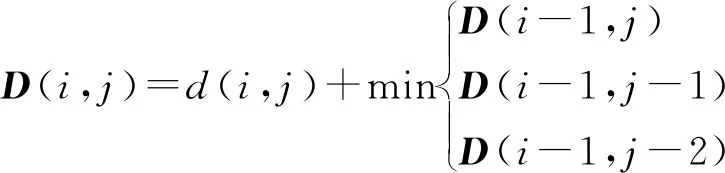
2.2 基于改进的DTW算法的地磁匹配方法
2.3 基于改进DTW算法的地磁匹配组合导航
3 仿真实验结果与分析

3.1 定位结果

3.2 算法运行效率

3.3 算法定位精度

4 结束语
