二值无偏测量与三值无偏测量的联合可测性

蒋颜君，张 林

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

量子测量是量子力学的特征之一。近年来，量子测量得到广泛研究，尤其是联合测量。文献[1]指出关于联合可测性的讨论需要从投影算子测度推广到正算子值测度；Yu等在文献[2]中讨论量子的两组测量的联合可测性，并得出一个明确的充要条件，同时在文献[3]中研究量子比特系统上的三组测量的联合可测性；此外，文献[4]证明了文献[2]中给出的两组二值无偏测量联合可测的充要条件；为分析给定测量的联合可测性，文献[5]引入W-测度，并根据文献[2-3]中得出的充要条件，分别讨论两组二值无偏测量的联合可测性和两组三值无偏测量的联合可测性；文献[6]研究一组测量的两两联合可测性与共同联合可测性的等价性。由于对二值无偏测量和三值无偏测量的联合可测性还未曾有明确的刻画条件，故本文研究量子比特系统上的二值无偏测量与三值无偏测量的联合可测性。

1 正算子值测度与W-测度

正算子值测度与W-测度及其负性的定义如下。

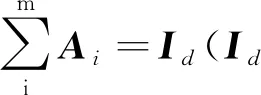
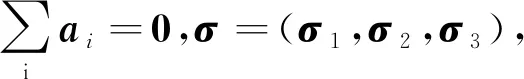
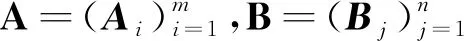
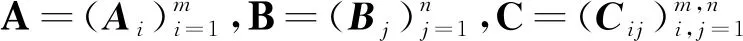
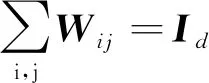
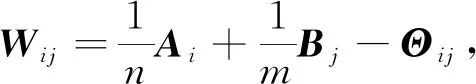
定义4[5]Cd上的W-测度的负性Ν(Θ)定义如下：

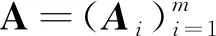
2 符号表示

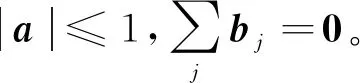
3 主要结论

在推导二值无偏测量与三值无偏测量的联合可测性条件之前，先介绍关于两组正算子值测度联合可测的命题[5]，即：

正算子值测度Α和Β是联合可测的，当且仅当Ν(Θ)=0。

利用上述命题，给出关于二值无偏测量与三值无偏测量的联合可测性的定理及其证明。

定理对于量子比特测量，Α=(A1,A2)和Β=(B1,B2,B3)分别为二值无偏测量和三值无偏测量，Α和Β是联合可测的充要条件为|a-b1+θ11|+|a+b1+θ11|+|a+b2-θ22|+|a-b2-θ22|+|a+b3-θ11+θ22|+|a-b3-θ11+θ22|≤6。

证明由文献[5]可知，正算子值测度Α和Β是联合可测的，当且仅当Ν(Θ)=0。此时有

(1)

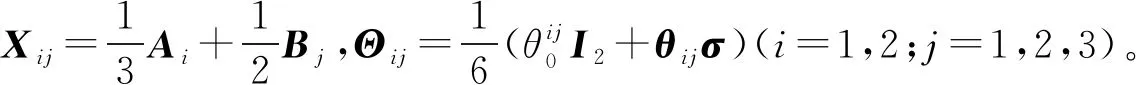
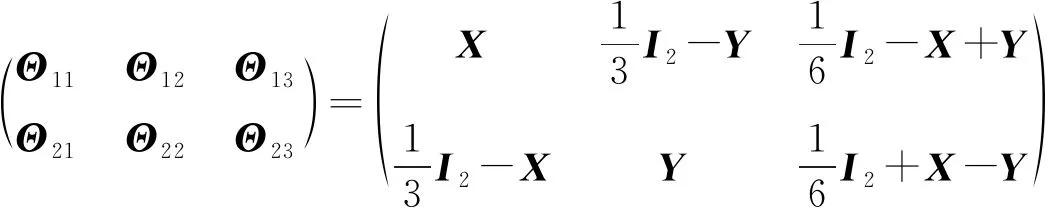
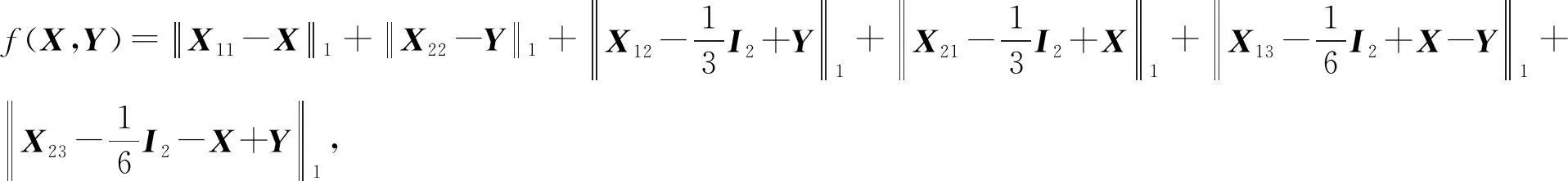
则有：

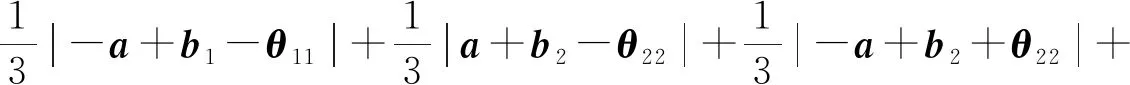
(2)

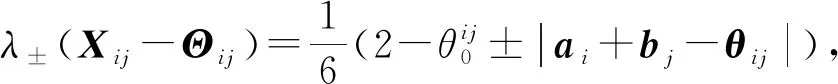
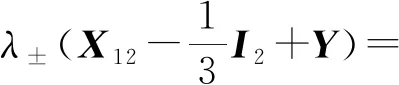
由λ-(X1j-Θ1j)+λ-(X2j-Θ2j)≤0(j=1,2,3)可以得到：

|a-b1+θ11|+|a+b1+θ11|≥2

(3)

|a+b2-θ22|+|a-b2-θ22|≥2

(4)

|a+b3-θ11+θ22|+|a-b3-θ11+θ22|≥2

(5)

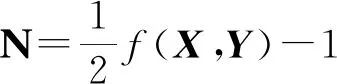
使用本文提出的二值无偏测量与三值无偏测量的联合可测性定理，通过一个实例来证明满足此定理条件的两组测量是联合可测的。

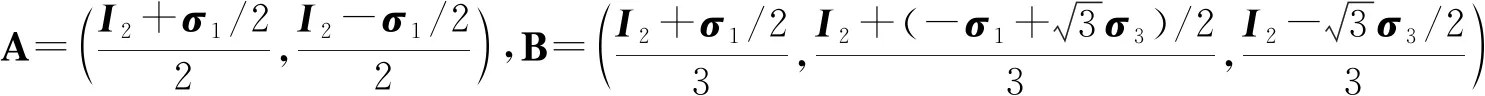
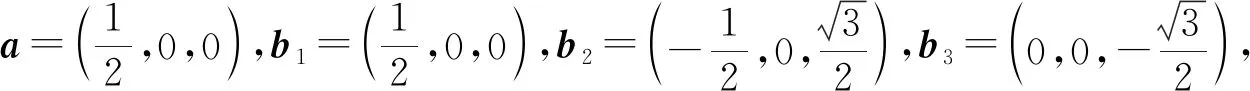
4 结束语

本文主要研究两组测量的联合可测性问题，即推导量子比特系统上的二值无偏测量与三值无偏测量的联合可测性条件。本文的研究可以推广到多组无偏测量联合可测的相关研究中，为有偏测量联合可测的研究提供一定思路。但是，本文暂未解决二值有偏测量与三值有偏测量的联合可测性，下一步将继续研究量子比特系统上的多组有偏测量的联合可测性。