移动传感器信息捕获的在线变速模型

徐文浩，程宗毛

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

覆盖问题是传感器网络设计中的热门研究方向，即传感器如何对区域内事件经常发生的位置即兴趣点(Point of Interest，PoI)进行监测，以最大限度捕获感兴趣事件的信息[1]。前期相关研究主要使用覆盖优化协议来优化传感器的任务子集，这类方法没有考虑移动传感器网络覆盖区域内随机事件的随机特性[2-3]。文献[4-5]的研究考虑了移动传感器网络覆盖区域内随机事件的随机特性，假设随机事件在PoI处发生的停留时间间隔和到达时间间隔服从参数固定的指数分布，得到移动传感器网络的节点调度方案。这类调度方案称为离线方案，也称为离线定速模型。但是，在实际应用中，由于各种因素的影响，不同时间得到的样本可能由分布参数不同的分布总体产生。因此，依据实际数据调整分布参数和更新节点调度很有必要，否则得到的结果偏差较大。本文从统计学角度出发，使用Bayes统计方法，把随机事件的分布参数由固定值转换为随机变量，提出一种移动传感器在线变速模型，实现了事件分布参数和传感器移动速度的实时修正，提升了移动传感器节点的监测质量和网络寿命。

1 移动传感器模型

假设n个PoI位于同一个几何区域内，每个PoI相连成为1条长度为L的环形路径，随机事件发生在这些PoI处，不同随机事件在这些PoI处的停留时间间隔X和到达时间间隔Y独立同分布于分布参数为λ和μ的指数分布总体[3]。1个感测半径为r的移动传感器以循环的方式监测这些PoI，并获取其感测范围内随机事件的信息，直到该传感器的能量耗尽。移动传感器在每轮循环中通过每个PoI仅1次。随机事件的信息积累随着移动传感器感测时间的增加而增加，感测效用函数分为2种[5]：

(1)阶梯效用函数：对于所有t>0，UI(t)=1，其中，t为传感器感测时间。

(2)指数效用函数：对于所有t>0，UA(t)=1-e-At，其中，A为信息漏检容忍度。

假设移动传感器的传感功能一直开启，并且通过控制传感器的移动速度v来控制循环一轮所需时间T，传感器在移动监测期间消耗的总能量为k1t+k2vθt。其中，k1,k2分别为传感器运动能量模型的比例参数和能量损失参数，θ为环境因素参数。

2 Bayes分析

2.1 先验分布

引理1对于随机变量X∈Exponential(λ-1)，其概率密度函数为：

P(X=x|λ)=λ-1e-x/λ

(1)

式中，x>0，E(X)=λ，λ>0为随机事件停留时间变量X的均值。

在统计决策理论与Bayes分析中，选用逆Gamma分布IG(α,β)作为λ的先验分布最为恰当，且IG(α,β)的密度函数为：

(2)

式中，λ>0，α>0，β>0为2个待定参数，λ的数学期望和方差分别为：

(3)

(4)

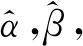
2.2 后验分布与Bayes估计

从Bayes统计理论出发，通过已知的先验分布π(λ)中获得1个观测值λ，再由参数为观测值λ的指数分布中获得n个随机事件停留时间间隔的样本观测值x1,x2,…,xn。此时样本观测值的联合密度函数为：

(5)

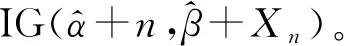
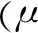
3 单位能耗捕获的预期信息量

由移动传感器模型可知，用移动传感器节点能量耗尽前捕获的信息总量与节点能量之比来表示单位能耗捕获的预期信息量(Expected Information Captured Per Unit of Energy Consumption，IPE)。IPE与监测效用函数和节点监测质量(Quality of Monitoring，QoM)有关。根据文献[5]和Bayes分析可以得到不同感测效用函数下EQoM和EIPE的计算公式。

(1)阶梯效用函数：

(6)

(2)指数效用函数：

(7)

式中，q=2r/v，p=L/v。

4 在线变速模型

在线变速模型的关键是求得移动传感器的可变速度v。首先，根据移动传感器模型得到节点单位能量捕获事件数；然后，结合分布参数的Bayes后验估计和单位能耗捕获信息量，利用牛顿迭代法求出可变速度v。

在移动传感器网络下，每循环一轮所需时间为L/v，所以传感器每循环一轮所消耗能量为：

每循环一轮所捕获的随机事件数为：

因此，移动传感器单位能量事件捕获数为NE=Nc/E1。

当给定分布参数Bayes估计值和单位能耗捕获信息量EIPE0时，通过求解式(6)和式(7)可以得到以NE为参数的非线性方程

(8)

用牛顿法迭代求解f(v)的零点近似值(即在线速度)的步骤如下。

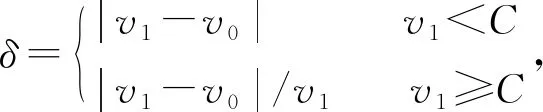
由式(8)和牛顿迭代法可以得到，不同Bayes参数估计值和节点能量效率下的移动传感器在线可变速度v。

5 模拟实验与分析

通过数值比较和模拟仿真实验来验证移动传感器在线变速方案的有效性。实验参数设置如下：(1)移动传感器感知半径为1 m，能量约束为29 160 J；(2)移动传感器能量运动模型比例参数为2.558 5 J/h，能量损失参数为15 J/h，环境因素的常量参数为0.5；(3)循环路径长度为2 000 m，PoI个数为15个。

表1 分布参数的实时修正结果

当监测区域内的PoI上发生的随机事件数N不断增加时，根据本文的Bayes理论分析和模拟实验计算可以得到，分布参数λ和μ的Bayes后验估计的实时更新结果如表1所示，N=0表示离线模型。

对于具有不同感测效用函数的随机事件，当分布参数随实际数据(样本)增大时，传感器移动速度v对单位能耗捕获信息量EIPE的影响如图1所示。从图1可以看出，无论传感器移动速度v如何变化，在线模型的EIPE均大于离线模型的EIPE；当EIPE相同时，在线速度v大于离线速度v，说明在线变速模型能够比离线模型捕获更多的随机事件，进一步降低了事件的漏捕率。

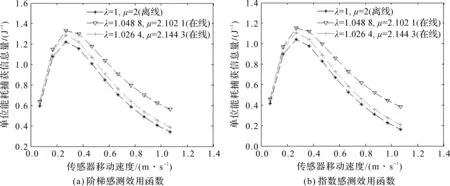
图1 不同感测效用函数下，速度对单位能耗捕获信息量的影响

对于具有不同感测效用函数的随机事件，EQoM=0.7，当分布参数随实际数据(样本)减小时，在线模型与离线模型传感器网络寿命对比情况如图2所示。从图2可以看出，在线速度v小于离线速度v，说明在相同的监测质量下，在线变速模型比离线定速模型节省更多的节点能量，延长了网络寿命。

图2 不同感测效用函数下，在线与离线传感器网络寿命对比

6 结束语

针对移动传感器离线模型在实际应用中误差较大的问题，本文从统计学角度出发，通过Bayes分析，提出一种传感器移动速度能够实时更新与修正的在线变速模型，提升了节点的监测质量和网络寿命。但是，本文研究的是电池容量有限的移动传感器，后续将对可充电移动传感器的在线变速问题展开进一步研究。