基于Khatri-Rao积的三维前视声呐空间方位估计技术

周 天 沈嘉俊 杜伟东* 周曹韵 宋金阳陈宝伟 李海森

①(哈尔滨工程大学水声技术重点实验室 哈尔滨 150001)

②(哈尔滨工程大学海洋信息获取与安全工信部重点实验室 哈尔滨 150001)

③(哈尔滨工程大学水声工程学院 哈尔滨 150001)④(中国电子科技集团第三十六研究所 嘉兴 314000)

1 引言

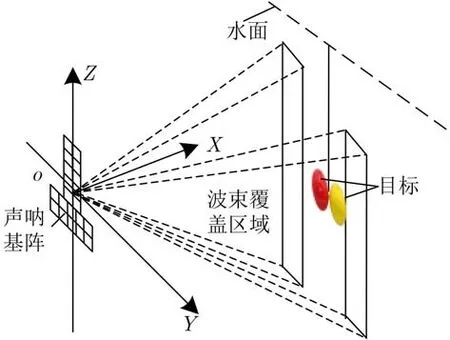
近年来，3维前视声呐作为一种重要的水下探测系统，在海底地形测绘、石油管道检测、沉船打捞、水下航行器避障、水下机器视觉等领域具有广泛的应用[1–3]。目前，国外多个公司已研制出实用化的3维前视声呐设备。从功能原理上，国际上把3维前视声呐主要分为两类：(1)相控扫描式3维前视声呐，如TriTech公司的Eclipse[4]，采用“T”型阵列结构，以水平向波束形成、垂直向扫描的方式完成3维探测，这种探测方式效率非常低；(2)多波束3维前视声呐，如CodaOctopus公司的Echoscope4G[5]，采用2维方形接收面阵设计，采用2维波束形成技术完成3维探测，然而系统实现成本非常高；相比之下，Reson公司的SeaBat 7130[6]采用2维矩形接收面阵设计，水平向采用波束形成技术，垂直向采用相干技术即可完成3维探测，相比Echoscope4G，该方案具有较低的系统成本。

3维前视声呐作为一种2维方位主动探测声呐，回波信号具有强相干的特点，也即来自不同方位回波信号的皮尔森相关系数约为1。因而在实际工程应用中，在考虑改善目标方位分辨性能的同时，还需考虑2维方位估计失效和信号相干的问题。围绕提高方位分辨能力这一目标，陈建等人[7]采用4阶累积量进行虚拟阵列孔径扩展，有效地改善了多目标分辨性能，然而4阶累积方法运算量非常大；杨永晶等人[8]采用Kronecker积构造虚拟协方差矩阵，相比4阶累积方法计算复杂度有一定程度降低，然而在时间序列上的Kronecker积处理引入大量冗余信息，系统实时性不够友好；韩佳辉和谭伟杰等人[9,10]直接对协方差矩阵进行向量化操作，基于Khatri-Rao积构造观测信号模型，相比Kronecker积处理，避免了时间维度引入的冗余，而仅仅对阵列孔径进行扩展，进一步降低了计算复杂度。此外，本文所述3维前视声呐还存在信号相干的问题，4阶累积量、Kronecker积等进行虚拟阵列扩展将出现协方差矩阵秩亏损的问题。为了恢复矩阵的秩，现阶段主要有降维处理和非降维处理两类方法进行解相干操作。其中降维处理方法以空间平滑类算法为代表，然而这类算法是以阵列孔径损失作为代价[11]；非降维处理方法有效避免了阵列孔径损失[12]。基于Khatri-Rao积方法在进行去冗余操作时隐含协方差矩阵平滑过程，有效避免了阵列孔径损失。值得注意的是，自协方差矩阵将抵消回波信号模型中垂直角时延分量(见本文3.1节)，应用于前视声呐的2维方位估计方法将失效，因而，上述4阶累积、Kronecker积、Khatri-Rao虚拟孔径扩展技术不能直接应用于文献[13,14]中所述的2维方位估计方法。

围绕提升目标分辨能力这一目标，本文重点解决现有阵列扩展技术存在2维目标方位估计失效、协方差矩阵秩亏损的问题，综合考虑2维稀疏面阵的结构特点，首先基于不同子阵构造互协方差矩阵，然后进行Khatri-Rao积扩展，提出单测量向量Khatri-Rao方法(Single Measured Vector Khatri-Rao, SVM-KR)和多测量向量Khatri-Rao方法(Multiple Measured Vector Khatri-Rao, MVMKR)，并进行了理论推导、计算机仿真和工程实现验证。通过仿真实验，验证了所提出方法在目标分辨能力方面优于文献[13,14]中所述的单测量向量波束形成(Single Measured Vector Beamforming,SVM-B)方法，计算复杂度低于4阶累积量和Kronecker积虚拟阵列扩展方法；通过水池目标探测试验，验证了声呐系统和相关算法的工程实用性。

2 问题阐述

2.1 稀疏阵列配置

自研前视声呐接收阵列配置如图1所示。接收阵列由3个均匀线性子阵构成，子阵间阵元间距分别为 5d 和3 d ，其中每个子阵由 M个阵元构成，为了避免相位模糊阵元间距为半波长d =λ/2[15,16]。因此，该阵列由 M ·I 个阵元组成，I =3,M =48。根据文献[1,13,17]，该2维稀疏面阵具有下面的优势：(1)适当改善目标方位估计分辨能力；(2)增强方位估 计方法对于噪声的鲁棒性；(3)避免相位模糊问题。

2.2 信号模型

如图2所示，在快拍号t ，考虑 K 个远场窄带相干回波信号同时入射2维接收阵列，第i行 第m 列阵元接收回波信号模型可表述为[16]

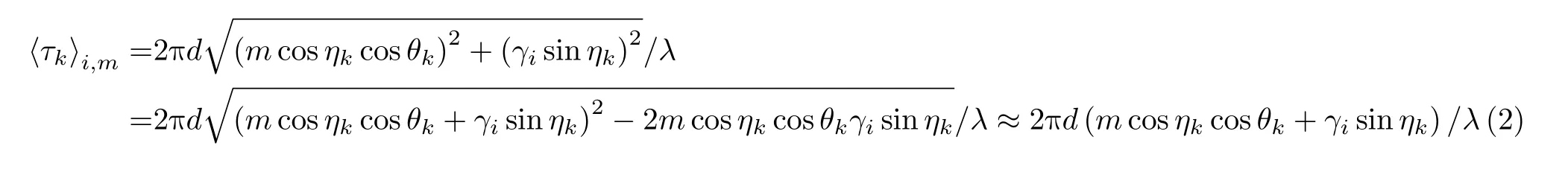
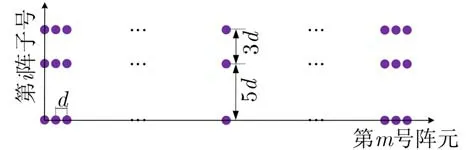
图1 2维稀疏接收阵列

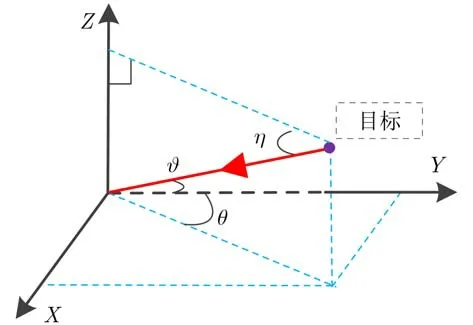
图2 3维笛卡尔坐标系下的目标方位表述

3 提出的算法

3.1 1维空间角估计方法

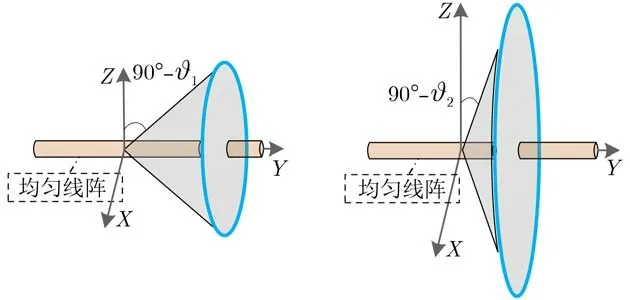
图3 导向波束的3维波束图案

进而，联系式(9)有

3.2 基于Vernier法[17,19]的垂直角估计方法

3.3 基于最小角定理的水平角估计方法

3.4 虚拟扩展阵列特性分析

(1)虚拟阵元接收信号相关性分析。如本文所述3维前视声呐，接收回波信号具有相干的特点，协方差矩阵的秩为1，应用本文所提方法进行虚拟阵列扩展，扩展后的虚拟阵元接收信号仍具有相干的特点。经过Khatri-Rao积向量化投影变换，等效为矩阵平滑，得到一个满秩协方差矩阵，可恢复为非相干信号模型[9,10]。

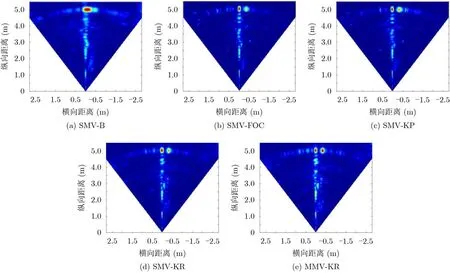
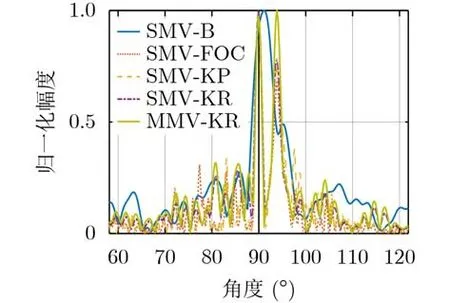
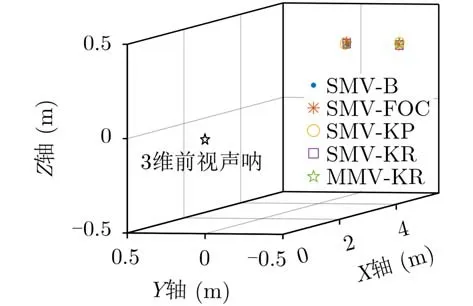
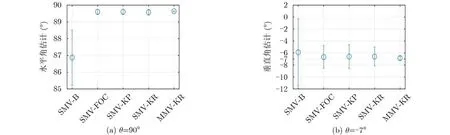
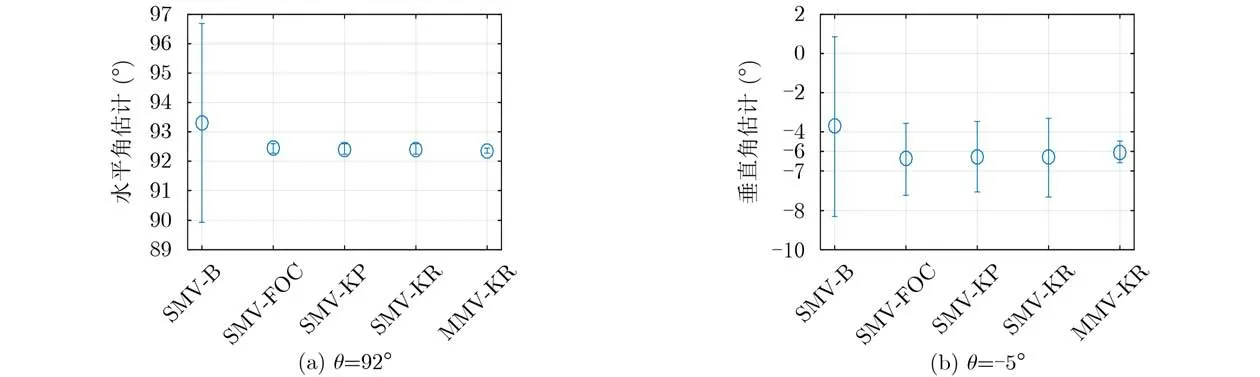
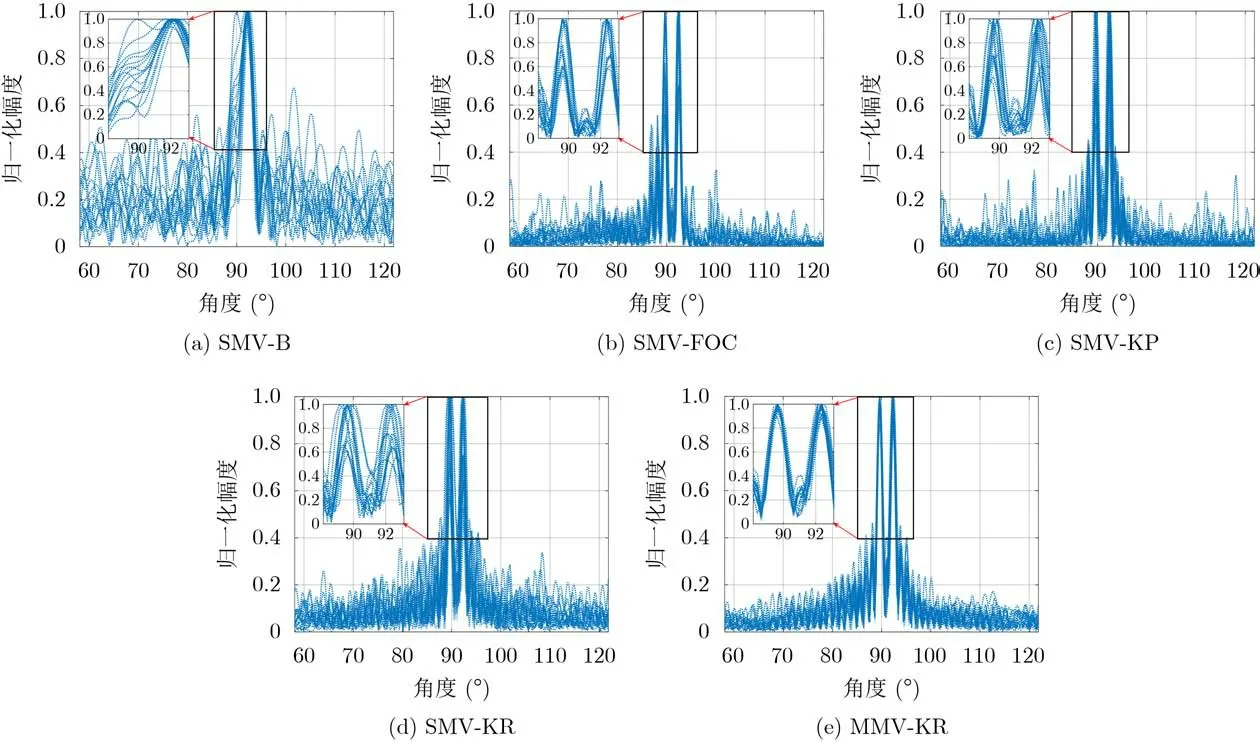
其中， β为–3 dB加权窗系数，例如当窗函数为矩形窗时， β ≈0.443 。a rc sin(·)函 数在[ 0,π/2]区间内单调递增，我们有 BWKR,−3dB

4 仿真实验及分析

4.1 仿真实验

考虑两个窄带相干回波信号，水平角分别为90°和92°，垂直角分别为–7°和–5°，根据式(18)空间角分别为90°和91.99°。信噪比–5 dB，采用单测量向量4阶累计方法(Single Measured Vector Fourth-Order Cumulant, SMV-FOC)[7]、单测量向量Kronecker积方法(Single Measured Vector Kronecker Product, SMV-KP)[8]、SMV-B[13,14]、本文第3节所述SMV-KR和MMV-KR进行空间角估计，SMV-FOC, SMV-KP, SMV-B和SMV-KR方法中L=1, MMV-KR方法中L =3，1000次独立的蒙特卡洛仿真实验水平角、垂直角估计误差棒图如图4、图5所示，其中15次输出波束图案如图6所示。

图4 目标1(水平角90°垂直角–7°)仿真估计结果误差棒图

图5 目标2(水平角92°垂直角–5°)仿真估计结果误差棒图

图6 仿真实验输出波束图案

本文中取波束图案上两目标间幅值下降3 dB(0.707)作为分辨准则。由图6可见，SMV-B方法不能分辨出两个目标，而SMV-FOC, SMV-KP,SVM-KR和MMV-KR方法均能分辨两个目标，验证了本文所提方法在多目标分辨方面的优势，此外，上述4种方法估计均值均较为接近真值，验证了2维目标方位估计能力。相比SMV-B方法，SMV-FOC, SMV-KP, SVM-KR和MMV-KR方法具有更低的估计误差，这是由于估计误差随着阵列孔径的扩展而降低。进一步地，相比SVM-KR方法，MMV-KR方法具有更低的估计误差，这是由于估计误差随快拍数的增加而降低。

4.2 计算复杂度分析

上述5种算法的计算复杂度差异主要集中在1维空间角估计这一操作，本文重点对这一过程进行分析。计算复杂度由flops(floating-point operations per second)的次数近似表示，一个flops定义为一次浮点加法或乘法操作。SMV-B, SMV-FOC, SMVKP, SMV-KR和MMV-KR方法的计算复杂度约为O(3M ·B) , O(4M5+8M4−2M3+13M2−8M+2+4MB·(2M −1)) , O(6M3+8M2−8M +2+4MB·(2M −1)) , O (2(2M −1) · B+4M3) 和O(4M3+4M2+2B·(2M −1))，因而计算复杂度方面所提出 的算法优于SMV-FOC和SMV-KP。

5 水池试验及分析

为进一步检验上述算法的有效性，本文依托哈尔滨工程大学研制的3维前视声呐于哈尔滨工程大学水声技术重点实验室信道水池开展实验研究。3维前视声呐关键参数如下。工作频率：150 kHz；发射波束宽度：60°×20°；接收波束宽度：2°×20°；阵列构成参数： M=48, I =3；探测信号：CW脉冲，脉宽0.2 ms。信道水池宽6 m，水深5 m，距离声呐基阵5 m处放置两个塑料球目标，声呐基阵置于水面以下2.5 m，目标置于水面以下2.2 m。水池实验场景示意图如图7所示。

如图8为上述SMV-B, SMV-FOC, SMV-KP,SVM-KR和MMV-KR方法应用波束形成技术输出的声呐图像，SMV-B方法不能很好地分辨两个目标，而SMV-FOC, SMV-KP, SMV-KR和MMVKR能较好地分辨两个目标，为了更清楚地说明这一问题，从上述5种处理方法中抽取某一快拍下的波束图案如图9所示，SMV-B方法由于波束宽度较宽，不能有效分辨出两个目标，而SMV-FOC,SMV-KP, SMV-KR和MMV-KR方法由于扩展了阵列孔径，波束宽度较窄，能够很好地分辨两个目标。最后，应用上述3种方法得到目标估计结果如图10所示，SMV-FOC, SMV-KP, SVM-KR和MMV-KR方法能够对水池中目标水平角、垂直角进行估计，联系回波到达时间，可完成目标的3维定位。

6 结束语

图7 水池实验场景示意图

图8 波束形成输出声图像

图9 某一快拍下的波束图案输出

图10 2维方位估计结果

本文依托2维SVM-B方位估计方法，基于Khatri-Rao积进行虚拟阵列扩展，提出1维空间角估计方法、基于Vernier法的垂直角估计方法和基于最小角定理的水平角方位估计方法。相比SVMB方法原有的阵列流型，在保证2维方位估计方法有效的前提下，扩展了阵列孔径并改善了目标分辨能力。仿真实验验证了所提出的SVM-KR和MMV-KR方法在目标分辨性能优于SVM-B方法，且方位估计精度更高，计算复杂度低于SVM-FOC和SMV-KP，水池实验进一步验证了本文所提方法能够对多目标进行有效分辨，具备较强的工程实用性。