基于正交移动双水下自主潜航器的水下合作目标定位方法

赵 晨 乔 钢 周 锋

(哈尔滨工程大学水声技术重点实验室 哈尔滨 150001)

(工业和信息化部海洋信息获取与安全工信部重点实验室(哈尔滨工程大学) 哈尔滨 150001)

(哈尔滨工程大学水声工程学院 哈尔滨 150001)

1 引言

近年来，随着水声及无线通信技术的发展，水下传感器网络在海洋资源开发，水下环境获取，水下目标探测等领域具有越来越重要的作用[1,2]。随着水声通信技术的不断进步，基于水声通信网络中的目标定位方法也成为了水声技术研究的热点课题[3]。

大范围水下目标定位常用于远海，深海目标定位，具有较大的应用背景，是水声定位研究的主要方向之一[4]。传统大范围水下目标定位方法，利用水下传感器组网实现定位。基于水下传感器网络的定位方法，需要利用布置在海底的潜标节点作为锚点，利用目标与锚点之间的通信完成定位过程。通常采用目标与节点间的信号传播时延测量(Time-Of-Arrival, TOA)或信号传播时延差(Time Difference Of Arrival, TDOA)的测距定位方法，或者利用测量目标到各个接收信号之间的方位角(Angle Of Arrival, AOA)和利用多跳信标间通信(DVHop)的非测距定位方法[5–7]。在大范围海域中，通过增加网络中通信节点个数，可以有效扩大定位覆盖范围[8]。该种方法在定位范围增加的情况下，通信节点个数需要成倍数地增长，并且需要在定位前布置好水下节点的位置，不利于未知区域定位和隐蔽定位。另一种常规方法采用区域划分，对定位区域进行划分，每个区域内，利用水面甲板单元携带的大型超短基线基阵，对目标进行定位[9]。该方案对设备要求较高，定位过程耗时长，并且不适用于深远海目标定位。

近年来随着水下导航技术和移动传感器技术的不断发展，水下无人潜航器(Untethered Underwater Vehicle, UUV),水下自主潜航器(Autonomous Underwater Vehicle, AUV)和水下机器人(Remotely Operated Vehicle, ROV)有了越来越多的应用场景[10,11]。基于移动传感器的目标定位方法是水声定位技术的一个新的研究方向。现有水下移动节点通常载体上携带惯性导航系统( Inertial Navigation System, INS)，多普勒速度计(Doppler Velocity Log, DVL)和陀螺仪等设备，可以较为精确地计算出自身在水下的导航位置[12,13]。以AUV定位为例，相较于传统的基于多信标测距的长基线定位方法，采用这种定位方法对水下载体定位时只需要利用少量AUV对目标进行定位，占用资源少，具有重要的应用价值[14,15]。

目前，一些基于AUV的定位方法也被逐渐提出，文献[16]中提到了一种基于虚拟长基线定位单AUV定位方法，该方法利用一个固定在水下的潜标节点，和一个具有导航装置的AUV，利用声信号传播的时间可以确定目标与海底声信标之间的距离。通过AUV的多次运动，建立虚拟水下潜标节点，实现虚拟信标定位。但该方法需要借助海底潜标节点进行辅助定位，并且至少需要3次以上AUV运动才可以确定目标位置。文献[17]中，针对AUV定位中区域声速不同问题，提出了一种利用卡尔曼滤波器进行弯曲补偿的改进方法，有效地降低了定位过程中声速误差对定位结果的影响，提高定位精度，但该方法对节点间的时间同步要求较高。

针对单AUV目标定位中存在的单次定位过程中通信次数长和时间同步问题，本文提出了一种基于正交运动的双AUV定位方法，利用两个运动航向角呈90°的AUV完成定位。定位过程中静止目标通过测量到每个AUV间的通信时延差，进行双曲定位。有效降低了定位的同步误差，并且降低定位过程中的通信次数。

2 基于单移动AUV静止目标定位方法

基于单AUV的移动定位方法，利用AUV移动过程中，测量多次通信间隔中待定位静止目标收到来自AUV的信号到达时间实现定位，定位原理如图1所示。

通常每个AUV可以利用携带的惯性导航系统和陀螺仪测得自身航迹位置。AUV运动姿态由航向角，俯仰角和横滚角描述，假设移动AUV航向角为Ψ，俯仰角为θ，横滚角为φ，则AUV运动坐标系{B}与大地坐标系{L}之间的转移矩阵RLB为[18,19]

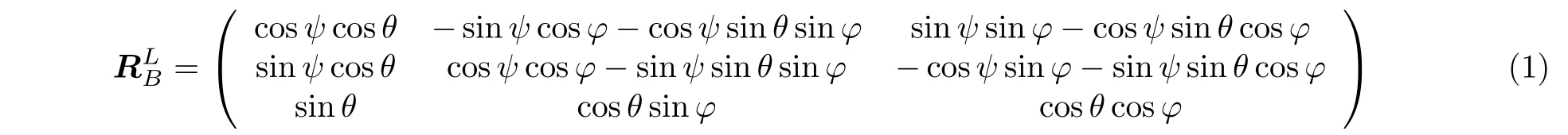
若AUV相对运动坐标系的移动速度为v，则经过t时刻AUV移动距离L为

初始位置已知时，AUV可以通过速度v和时间t计算自身坐标位置。通常AUV和静止目标的深度信息可以通过压力传感器测量，静止目标T (x, y)与AUV每次通信间间距li可以由声速c和通信时间ti计算

根据球面交汇的几何模型[3]，静止目标经过最少3次与AUV之间的通信，可以计算自身位置。如

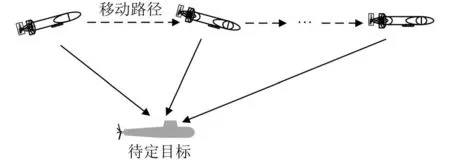
图1 单移动AUV静止目标定位示意图

图2所示，假设经过n次通信后，AUV每个通信位置记录自身坐标分别为(x1, y1), (x2, y2), ···, (xi, yi)根据距离关系

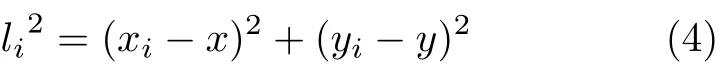
经过化简并利用最小二乘法进行求解[20,21]，整理得到

基于单AUV移动的静止目标定位方法，至少需要3次AUV与静止目标间的通信实现定位。AUV移动路径较长，由于AUV自身的INS系统的累积误差，使得多次移动间AUV自身位置误差增加，同时AUV与静止目标间的时钟同步存在误差，导致单AUV静止目标定位误差较大。

3 基于正交移动AUV静止目标定位方法

3.1 基于正交移动AUV算法实现

针对单移动AUV利用惯性导航系统对静止目标多次通信间隔完成的定位误差问题，本文提出了一种基于正交运动的AUV静止目标定位方法，原理如图3所示。

该定位方法由两个运动路径规划互相呈90°的移动AUV实现。定位原理如图4所示，假设2个AUV初始坐标标分别为A1(x1, y1), B1(x'1, y'1)，与待定位静止目标距离分别为r1, d1，当声速为c，静止目标接收到A1与B1信号到达时间分别为t1和t'1，根据距离坐标关系，可以得到

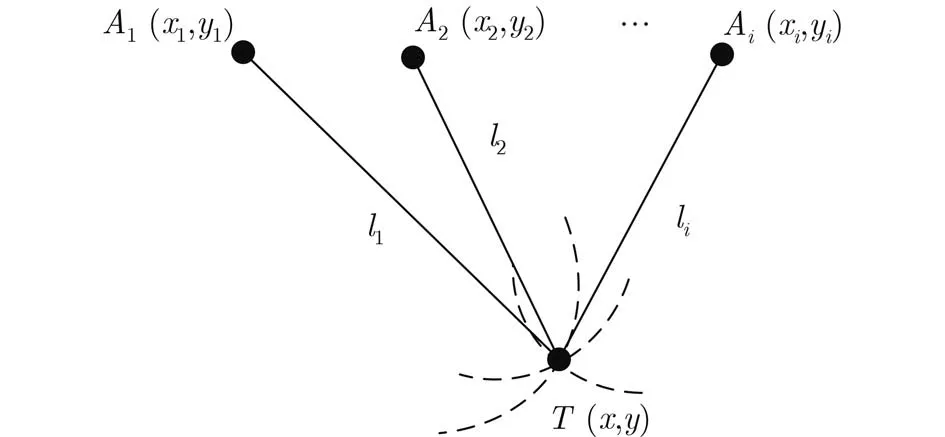
图2 单移动AUV球面交汇算法原理示意图

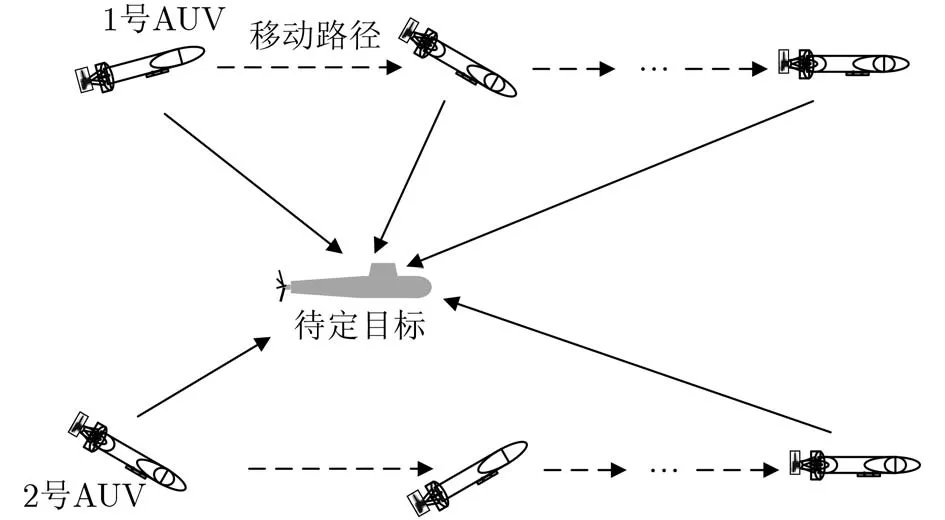
图3 正交运动AUV静止目标定位示意图

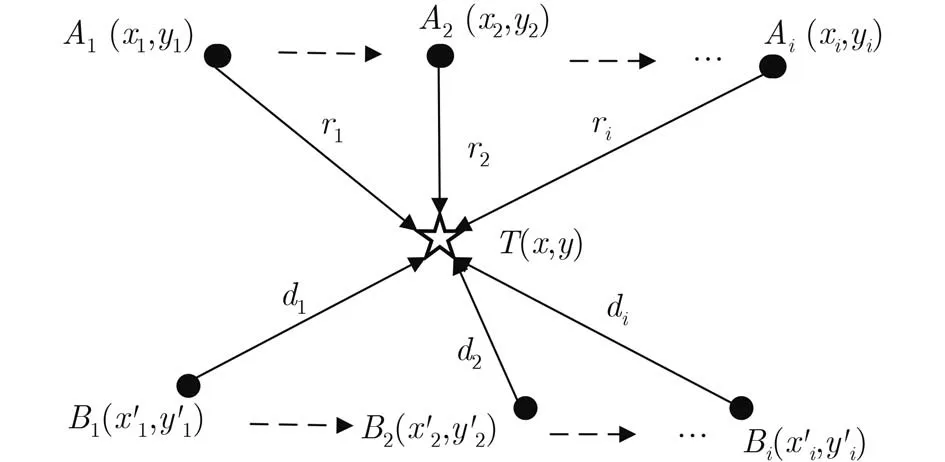
图4 正交运动AUV定位算法原理示意图

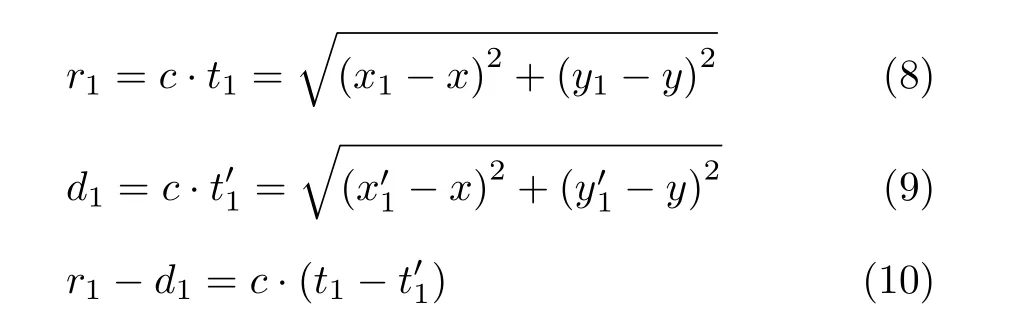
其中，t1– t'1为信号到达时延差。在经历1次通信间隔后，AUV分别移动至坐标A2(x2, y2), B2(x'2,y'2)，静止目标接收到A1与B1信号到达时间分别为t2和t'2，根据式(8)和式(9)，同理得到

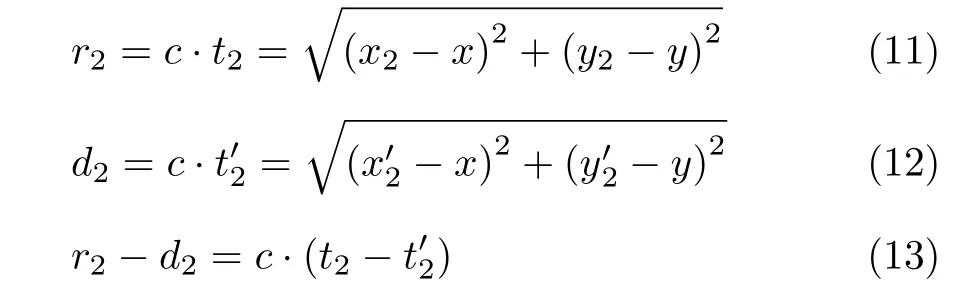
同理t2– t'2为静止目标经历1次通信间隔后接收到AUV信号的时延差。整理式(8)—式(13)，静止目标与AUV之间的距离关系为

利用式(18)—式(20)待定位静止目标最少可以通过每个AUV 1次运动过程和静止目标间的2次通信，实现静止目标定位。当AUV多次运动，再移动i–1个周期后两个AUV分别移动至Ai(xi, yi),Bi(x'i, y'i)，则重复式(8)—式(20)推导步骤，同理可以计算经历AUV i–1次运动后静止目标位置为

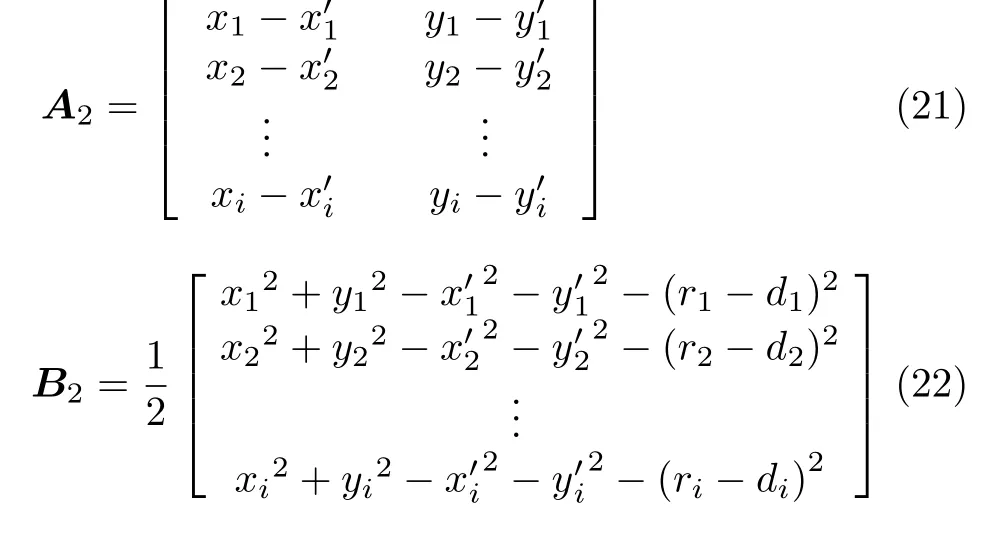
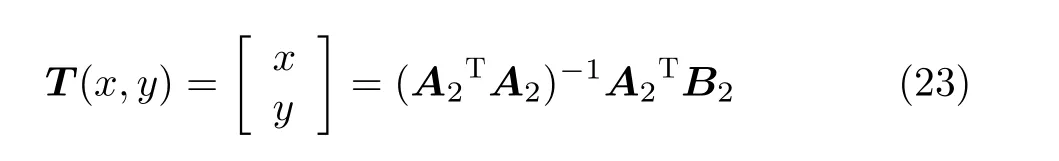
3.2 基于正交移动AUV定位过程实现

根据3.1节中的定位算法原理，本文设计了基于正交运动AUV定位方法。定位过程如图5所示，首先每个AUV进行自身位置校准和AUV与静止目标之间的时间同步校准。经过位置和时间校准后，AUV向静止目标发射带携带自身位置信息的通信信号，静止目标接收到信号后，记每个AUV位置坐标和AUV传输信号的到达时延差。随后AUV开始按照规划路线进行运动，经历1个时间周期后，通过自身INS系统确定所在位置，再将位置坐标通过通信信号发送给静止目标，静止目标记录每个AUV坐标和发送信号的到达时延差。以此类推重复上述过程，再经历i–1个AUV移动周期后，利用式(20)—式(22)即可解算出静止目标所在位置。

正交运动AUV定位流程图如图5所示。

4 仿真分析

根据本文提出算法，分别对单AUV移动定位和正交AUV移动定位做出仿真实验分析。仿真参数设置：定位范围设定50×50 km，声速c=1500 m/s,AUV的有效通信距离为10 km, AUV的运动速度为10 km/h, INS导航系统的平均累积误差为2 m/km，信号测时误差为100 ms，误差均服从高斯分布。两种定位方法中AUV的运动路线分别如图6(a)和图6(b)所示，其中横坐标为地理东向坐标，纵坐标表示地理北向坐标。

4.1 仿真实验1 区域定位误差分布实验

为了研究和比较单AUV移动定位方法和正交规划移动AUV定位方法的精度，设计定区域定位误差分布仿真，扫描区域50 km×50 km, AUV移动路按照图6中移动路线分别从起点位置移动到终点，静止目标扫描位置间隔为100 m，每个定位周期内静止目标与每个AUV完成3次通信，每个定位点定位20次并计算定位结果的均方根误差，仿真结果如图7(a)和图7(b)所示。根据仿真数据整理和统计，图7(a)的定位均方根误差最小值为103 m，中心区域平均误差为112 m，边缘区域最大误差为165 m，图7(b)的定位均方根误差最小值为70 m，中心区域平均误差为95 m，边缘区域最大定位误差为122 m。从图7中可以看出，正交移动AUV的静止目标定位方法，在精度上高于单AUV定位，并且其中蓝色覆盖区域明显大于单AUV定位的覆盖区域。

图5 正交运动AUV定位流程图

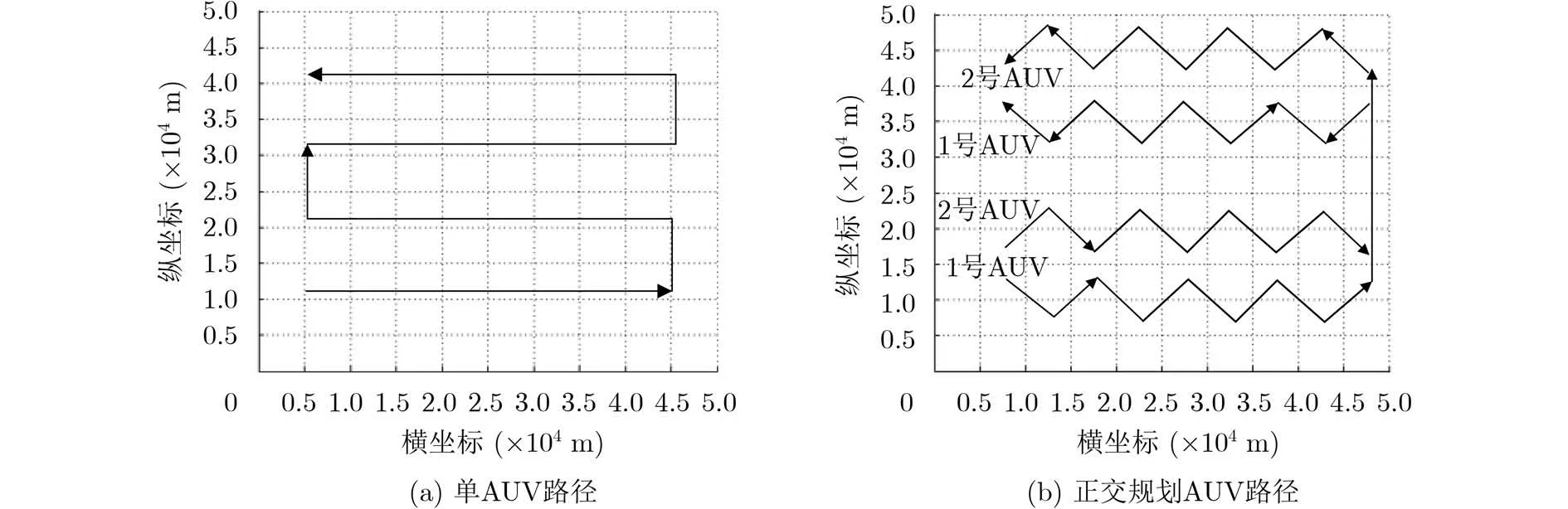
图6 单AUV运动路径规划图

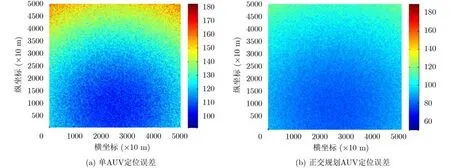
图7 两种定位方法定位误差分布图

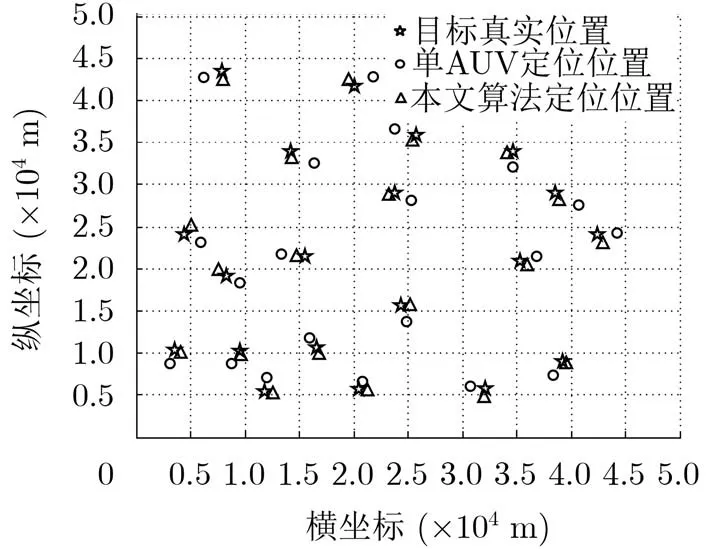
图8 随机位置静止目标定位结果图

为了进一步比较两种定位算法的定位效果，在区域内选取20个随机静止目标位置，记录真实位置，分别采用单AUV定位和正交运动的AUV定位方法实现定位，实验结果见图8。从图8中可以看出，下方区域采用两种方法的定位结果距离静止目标真实位置较近，本文提出的方法相比于单AUV定位的定位误差更小。随着AUV按照路径移动时间增加，导致INS系统的累积误差增大，AUV自身位置存在误差，图8中上方区域定位结果距离静止目标真实位置距离均有所增加，单AUV定位误差增加较大，本文提出的方法误差增加较小，并且定位结果优于单AUV定位。

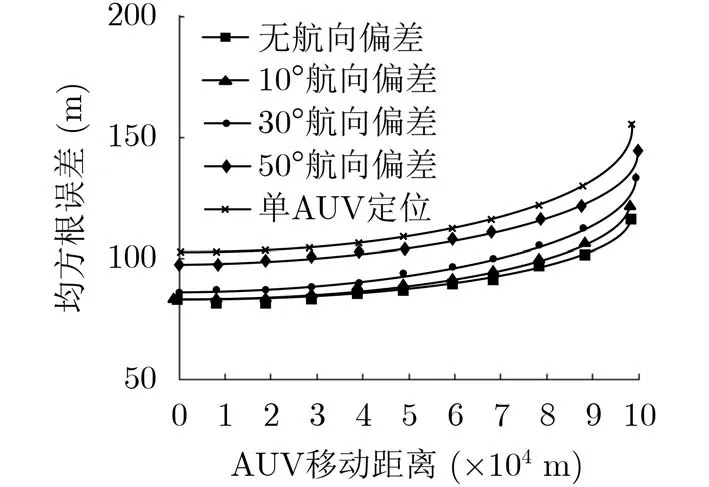
图9 不同航向角定位误差随AUV移动距离变化关系图

在实际应用中，由于受到洋流等海洋环境的影响，和AUV具体运动规划的需求，在实际应用中难以保证AUV规划路线的绝对正交。为了比较AUV导航误差对两种方法的影响，将图7中每个AUV路径的移动距离计算出，并与两种定位方法的误差值对应，并且分别引入10°, 30°和50°的航向偏差，结果见图9。从图9中可以看出，在AUV初始移动过程中，AUV自身导航误差对两种方法的定位结果影响不大。但随着AUV移动距离不断增加，每种方法的定位效果均有所下降。在正交运动AUV的航向角角度存在10°偏差时，定位效果与理想无航向角偏差情况效果相近，当航向角角度偏差增加到30°时，定位偏差有所增大，当航向角度存在50°偏差时，定位误差增加较大。但每种方法的定位效果均优于单AUV定位。在不同航向角角度规划的情况下，本文提出方法都有效的降低了AUV自身导航误差对定位精度的影响，正交规划效果最佳，在远距离长时间定位中有明显优势。

为了进一步研究时间同步对两种方法的影响，在4.1节的参数设置中，加入AUV与静止目标间的同步误差20 ms，定位结果见图10。从图10(a)和图10(b)中可以看出，在引入同步误差后两种算法的误差分布趋势基本相同，但相比于图7，单AUV定位的定位误差数值上明显增大，正交运动AUV误差影响变化较小。

为了进一步研究AUV航向规划角度偏差对定位精度的影响，将按照第4节中运动参数和图6(b)中AUV运动方向，分别设置规划路径中每个AUV的偏移航向角从0°～50°，每5°记录1次定位区域中心位置的均方根误差。

从图11中可以看出，当两个理想正交AUV航向产生10°的偏差情况下，定位精度基本相近，当航向角偏差由10°～30°增加时，该方法的定位误差略微增大，当航向角偏差大于30°时，该方法的定位效果存在一定程度的降低。

4.2 仿真实验2 不同通信周期定位误差实验

为了研究一个定位周期内不同通信次数定位精度的影响，设计对两种方法不同通信间隔的实验，使得每次定位需要2～10次静止目标与AUV之间的通信。其中，单AUV移动最少需要3次通信完成1次定位，正交移动AUV定位方法最少每个AUV需要2次通信。实验结果如图12所示。从实验中可以看出，对于两种方法，增加1次定位周期中AUV与静止目标间的通信次数可以降低定位误差，但随着通信次数增多，AUV移动的时间增加，导致AUV自身误差增大，在该参数实验下，每个定位周期内静止目标与每个AUV通信4次定位效果最明显，超过8次通信则定位精度降低。

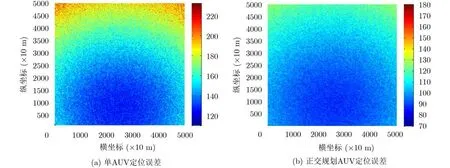
图10 加入同步误差后两种定位方法定位误差分布图

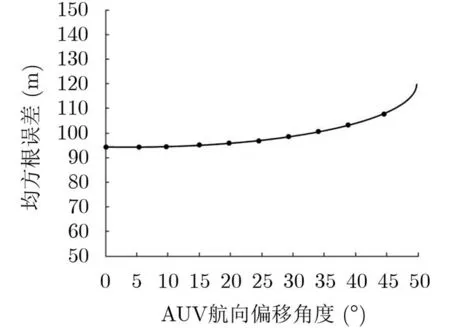
图11 正交定位误差与AUV之间航向角误差关系

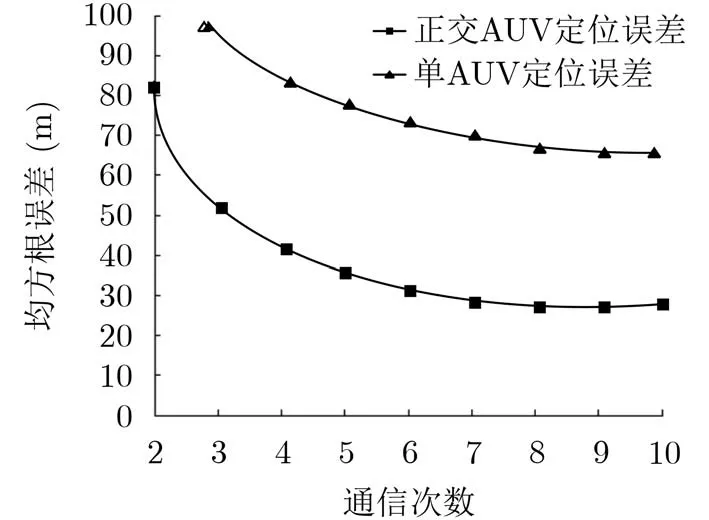
图12 定位误差与通信次数关系图

5 结束语

针对基于单移动AUV的静止目标定位方法存在定位通信次数多，定位精度低的问题，本文提出了一种正交运动的双AUV定位方法。该方法利用正交运动的AUV与静止目标间通信信号时间差，实现测距定位，有效地降低了AUV与静止目标间的时间同步误差。同时，本文方法相比于传统的单AUV定位方法，有效地降低了AUV自身导航系统在长期移动过程中累积误差对定位结果的影响，同时，本文方法相较于单AUV定位，有效地缩短定位周期，提高了定位精度。实验结果表明，本文提出的算法在定位精度，有效定位区域覆盖面积上都有一定程度的提高，为水下大区域静止目标定位提供可靠方案。但正交运动的双AUV定位方法，由于需要两个AUV作为参考节点，与单移动AUV的静止目标定位方法相比，增加了设备开销。