一种互谱相位在时延估计中的应用方法
2021-04-06张宗堂程玉胜
丁 超 陈 喆 张宗堂 程玉胜
(海军潜艇学院 青岛 266000)
1 引言
时延估计(Time Delay Estimation, TDE)是水声领域的重要研究课题,基于时延估计的水声目标被动测向、被动定位技术是水声目标无源定位的重要分支。目前,时延估计通常可以用于以下3类算法:基于时延估计的目标方位估计算法[1],基于时延估计的目标被动定位算法[2],联合其他观测量(如到达角度、到达频差等)的联合定位方法[3,4]。在以上各类水声目标被动测向和被动定位算法中,核心便是时延估计,时延估计的精度直接决定了测向和定位的精度。
本文结合互谱相位特征,设计了一种新的时延估计方法,在仿真实验中取得了较好的处理结果。
2 时延估计方法原理
2.1 时延估计基本模型
建立信号模型为
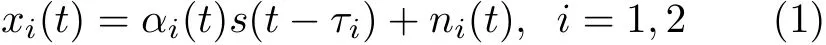
其中,xi(t)为 接收器i所 接收到的信号,s (t)为目标辐射噪声, τi为 s (t) 到达接收器i所 用的时间,αi(t)为s (t)到 达接收器i时 的衰减系数,ni(t)为 接收器i处的背景噪声。理想假设下,n1(t), n2(t)与 s (t)互不相关。
将衰减系数αi(t)简化为常量,为方便推导,在不影响模型本质的基础上,将信号模型简化为
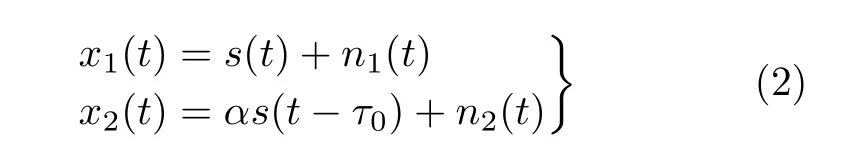
其中, α为目标辐射噪声到达两接收器时的衰减系数比值, τ0为目标辐射噪声到达两接收器的时间差。所谓时延估计即是通过x1(t)和 x2(t)来 推算τ0的计 算过程。
2.2 时延估计常用方法
目前,较为常用的时延估计方法有基本互相关法[5](Normalized Cross Correlation, NCC)、广义互相关法[6,7](Generalized Cross Correlation,GCC)和自适应时延估计[8,9](Least Mean Square,LMS)等。
2.2.1 基本互相关算法
求取两段波形最近似时的时延,经典算法便是基本互相关运算。结合式(2)信号模型,算式为
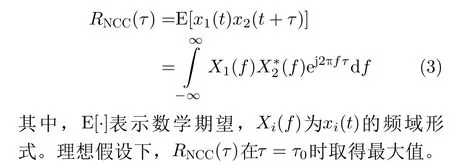
2.2.2 广义互相关算法
实际情况中,目标辐射噪声与背景噪声间通常不是严格的互不相关,且两路信号时长有限,背景噪声会影响相关运算结果,干扰时延估计精度。因此需要在相关运算之前对信号进行滤波,以达到抑制噪声、增强信号,从而提高时延估计精度的目的。结合式(2)信号模型,算式为


3 互谱相位时延估计算法
3.1 互谱相位时延估计原理
除以上算法之外,还可以利用互谱相位信息进行时延估计。结合式(2)信号模型,互谱算法为

通过求解互谱相位斜率,即可换算得到时延τ0[11–14]。假设存在单个目标且τ0=0.05s,理想情况下, φ(f) 为斜率2 πτ0的标准锯齿波,如图1(a)所示;非理想情况下,φ (f)为 斜率2 πτ0的叠加干扰的锯齿波,为两路宽带信号添加信噪比10 dB的高斯白噪声,信号时长5 s,采样率10 kHz,其互谱相位如图1(b)所示。
假设存在两个目标且两目标信号强度相同,为两路宽带信号添加信噪比10 dB的高斯白噪声,信号时长5 s,采样率10 kHz,其互谱相位如图2所示。
此时互谱相位谱可以视为多个锯齿波叠加干扰,可以表示为


图1 单目标互谱相位图
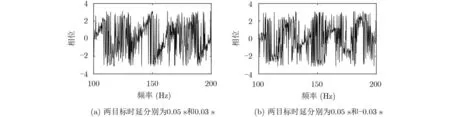
图2 非理想假设下双目标互谱相位图
3.2 现有互谱相位斜率求解方法及其限制
结合图1和图2,在互谱相位斜率求解过程中存在以下问题需要解决:
(1)互谱相位以2 π为周期变化,当相位变化超过2π 时,反正切函数的多值性会导致相位内卷。
针对该问题,目前较为常用的方法有相位拼接[15]、差分方法[16]等。相位拼接打破相位2 π的周期,通过周期间拼接,构造一条斜率2 πτ0的斜线;差分方法可将线性增量转变为常量,从而进行线性增量估计。但相位拼接需要在相位拼接之前先进行一次是否需要相位修正的预判断;差分方法需要在差分之后剔除相位在 −π 与π 之间突变所产生的峰值,再进行常量估计。两种方法均较为复杂,且准确性难以保证。
(2)受背景噪声干扰,互谱相位出现波动甚至是跳变的现象,会导致斜率估计误差增大。
针对该问题,目前较为常用的方法有最小二乘、等权平均[17]等。最小二乘法对相位数据进行线性拟合,以求得斜率参数;等权平均采用多点取样并平均,以求得一个无偏的斜率估计。这两种方法若想提高估算精度、提升抗噪能力,需要增加输入点数、扩大输入范围,但在计算互谱相位斜率时,输入范围往往受限。
(3)当存在多目标时,互谱相位可能存在两种情况:其一,形状杂乱,无法计算斜率;其二,偶有斜率,是由多目标相位斜率叠加而成。这就导致目前各种直接计算相位斜率的算法都将不再适用。
正是由于以上困难,导致基于互谱相位斜率的时延估计方法难以用于实际复杂情况,本文正是针对以上困难设计了一种间接求取互谱相位斜率的算法,适用于强干扰、多目标的情况。
3.3 互谱相位斜率求解方法
根据傅里叶变换的线性特性,结合式(8),可得多目标互谱相位的傅里叶变换为
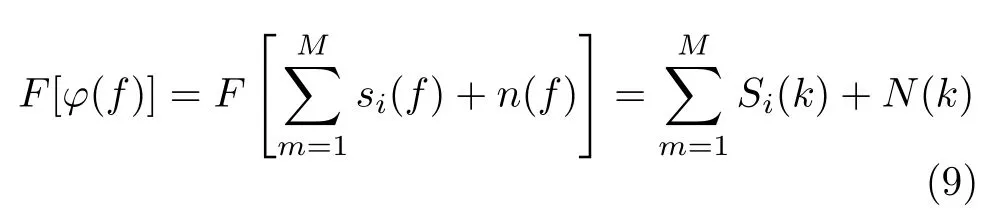
其中,Si(k), N (k)分 别为si(f), n (f)的傅里叶变换。
可见,多目标互谱相位在频域上相互叠加,加之噪声干扰,难以直接求取相位斜率。但在进行傅里叶变换后,各目标互谱相位将以线谱形式分离,线谱位置能够反映相位斜率大小,也就能进一步换算成时延大小。进行傅里叶变换后,通常的做法是对其取绝对值,但当输入信号是互谱相位时,绝对值结果仅能反映相位斜率大小,不能反映相位斜率正负,也就无法确定时延正负,这会造成时延估计模糊。
根据周期信号傅里叶变换公式

由式(12)可知,锯齿波傅里叶变换虚部在 f0处的值为a,其正负对应锯齿波斜率的正负,如图3所示。
可见,斜率为正的锯齿波,其傅里叶变换虚部基频处值为正;斜率为负的锯齿波,其傅里叶变换虚部基频处值为负。在互谱相位的处理中,互谱相位傅里叶变换虚部的线谱处横坐标值即为两路信号时延估计绝对值,线谱处数值的正负可以反映时延的正负。
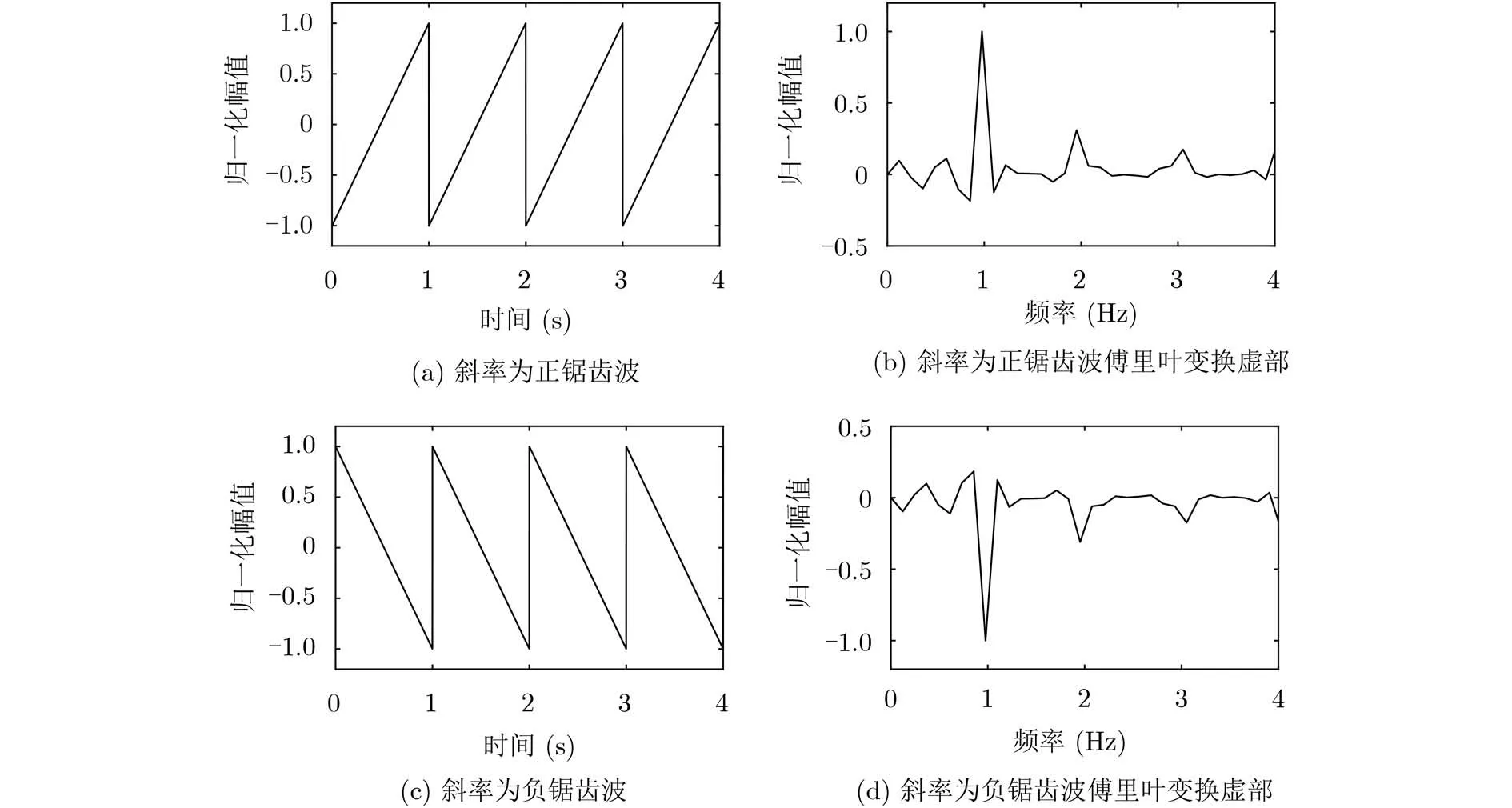
图3 锯齿波及其傅里叶变换虚部
至此,依据互谱相位进行多目标时延估计的条件已经完备。本文据此设计出一种新的利用两路信号互谱相位傅里叶变换域进行时延估计的算法,以互谱相位傅式变换法(Fourier transform domain of Cross-power Spectrum Phase, FCSP)表示,FCSP算法流程如图4所示。
FCSP算法具有以下特点:
(1)利用互谱相位斜率进行时延估计,不会产生时延估计模糊;
(2)解决了现有的互谱相位斜率求解算法的诸多不便,不再受制于相位模糊,且能够实现多目标分辨;
(3)通过多个互谱相位周期的累计,该算法具备较强的抗噪能力。
4 算法效果仿真比较
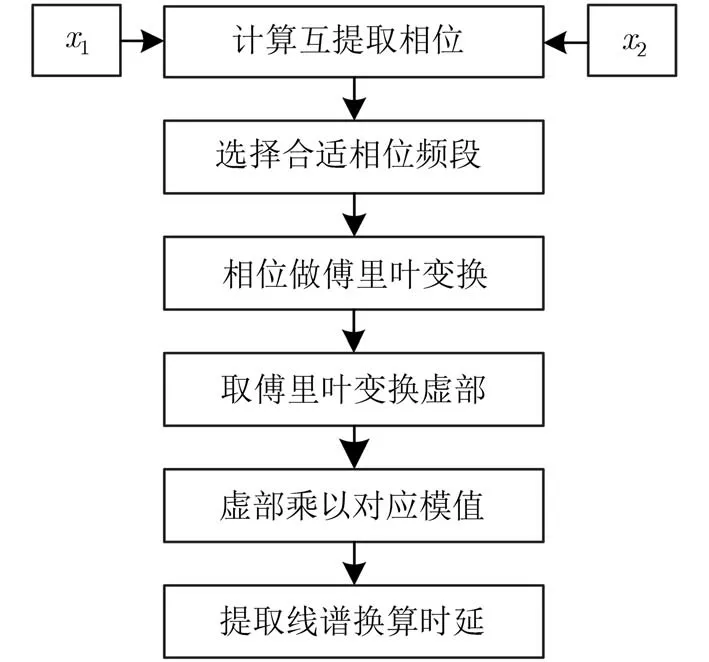
图4 FCSP算法流程图
LMS方法相当于一种迭代实现的GCC时延估计方法,效果与GCC方法一致,故本文仅对NCC,GCC与FCSP 3种算法展开比较,其中GCC算法采用常用的相位变换(PHAse Transform, PHAT)加权,即 ψ(f)=1/|Gx1,x2(f)|,该加权函数能够锐化广义互相关函数,突出时延峰值[18]。下面进行几种情况下的仿真效果对比。
4.1 多目标情况
假设存在两个目标且时延分别为0.05 s和0.03 s,为两路宽带信号添加信噪比–5 dB的高斯白噪声,信号时长5 s,采样率10 kHz,3种方法的时延估计结果如图5所示。
为验证算法性能,在3种算法计算结果归一化之后,分别求取其噪声的均方根误差(Root Mean Squared Error, RMSE), RMSE越小则表示算法性能越好。进行3000次Monte Carlo仿真实验,结果如表1所示。
由表1可知,FCSP算法结果线谱信噪比最高,最利于时延估计,GCC算法次之,NCC算法较差。
4.2 存在强窄带信号情况
假设存在两个目标且时延分别为0.05 s和0.03 s,目标信号包含50 Hz的强窄带信号,为两路宽带信号添加信噪比–5 dB的高斯白噪声,信号时长5 s,采样率10 kHz,3种方法的时延估计结果如图6所示。
由图6可见,NCC算法无法消除强窄带信号的干扰,当阵列最大时延大于窄带信号周期时,便会出现时延估计模糊,对时延估计结果造成严重干扰。而GCC算法和FCSP算法可以消除时延估计模糊,且该情况下FCSP算法结果线谱信噪比更高。
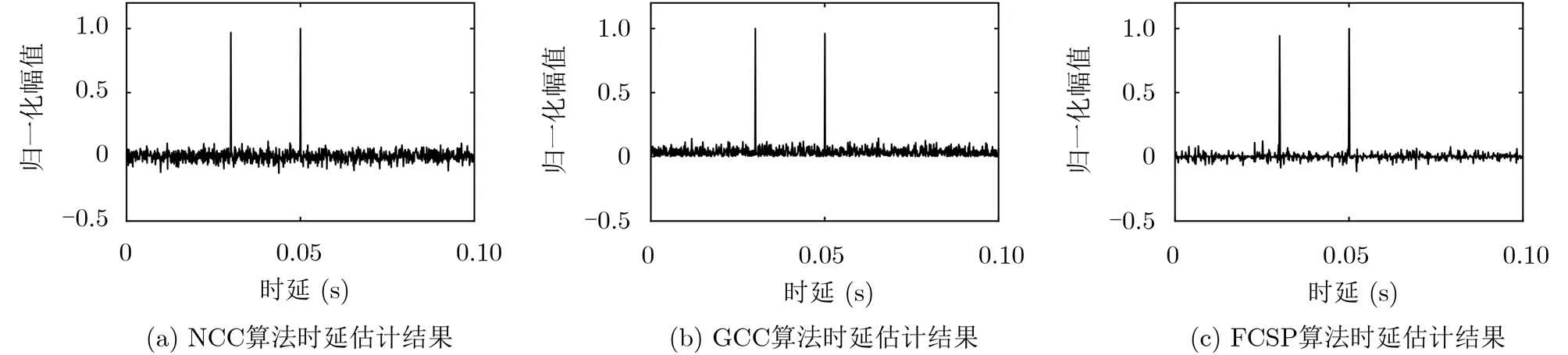
图5 多目标情况下3种算法性能比较

表1 3种算法噪声RMSE均值对比
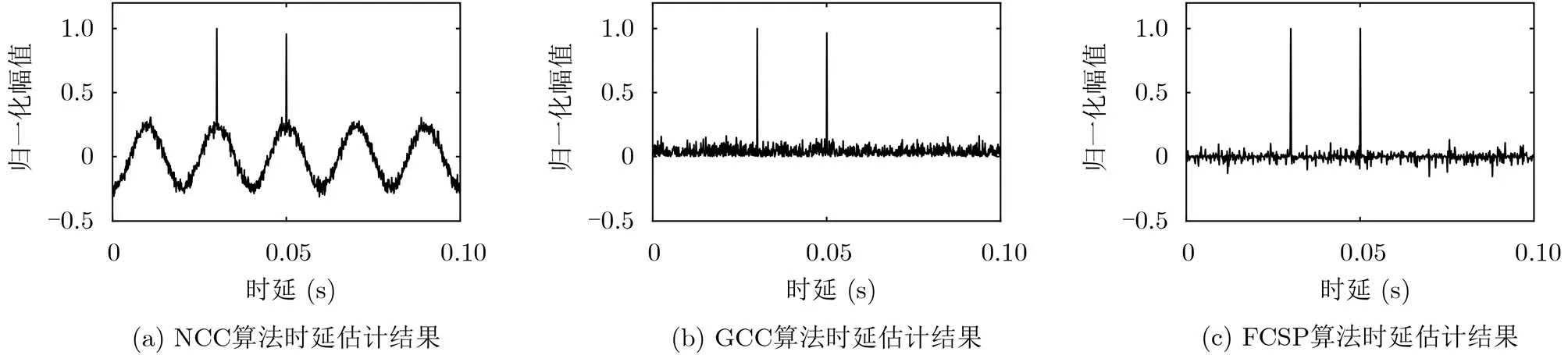
图6 存在强窄带信号情况下3种算法性能比较
4.3 背景噪声起伏情况
假设存在两个目标且时延分别为0.05 s和0.03 s,存在背景噪声起伏,为两路宽带信号添加信噪比–5 dB的高斯白噪声,信号时长5 s,采样率10 kHz,3种方法的时延估计结果如7所示。
由图7可见,NCC算法无法消除背景噪声起伏的干扰,而GCC算法和FCSP算法可以消除,且该情况下FCSP算法结果线谱信噪比更高。
综合3种情况来看,本文设计的FCSP算法能够分辨多个目标,可以消除强窄带信号及背景噪声起伏的干扰,且具备较强的抗噪能力,在信噪比较高的情况下,输出结果相较于GCC算法谱线信噪比更高。整体来看,FCSP算法处理效果优于NCC算法及GCC算法。
5 结束语
不同于目前常用的时延估计方法,本文从信号互谱相位角度出发设计了FGSP算法,利用两路信号互谱相位的傅里叶变换域进行时延估计,并在仿真实验中获得了较好的处理结果。
(1)FGSP算法的设计是基于傅里叶变换的性质及互谱相位的特点,解决了一部分现有互谱相位斜率求解算法未解决的问题,准确求取互谱相位也就意味着准确求取了信号时延;
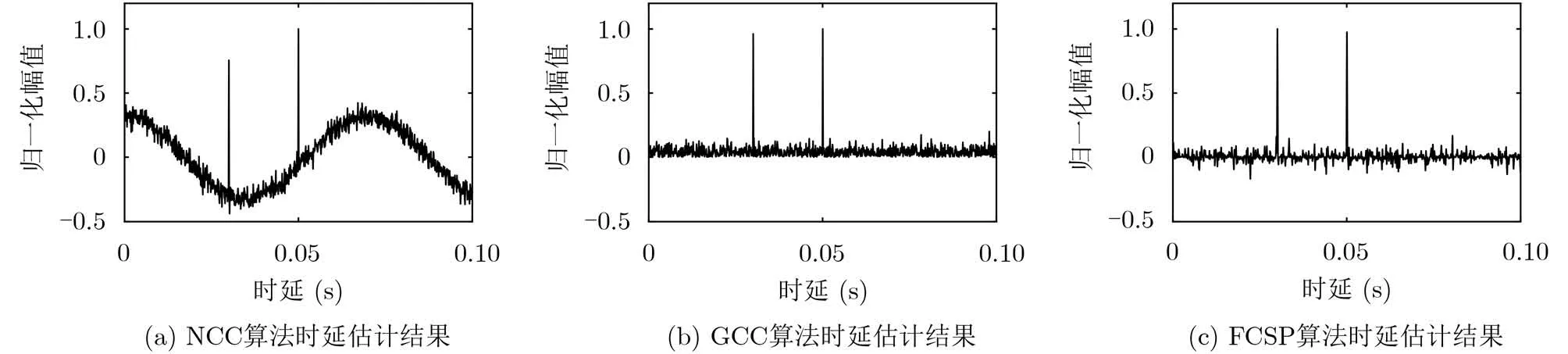
图7 背景噪声起伏情况下3种算法性能比较
(2)FGSP算法具备了多目标分辨能力、抗时延模糊能力、抗背景噪声起伏能力及良好的抗噪能力,仿真效果整体优于NCC算法及GCC算法;
(3)FGSP算法的流程及思路不同于目前常用的NCC, GCC及LMS等算法,在后续的工作中,FGSP算法流程的各步骤还可进一步优化或者融入新方法,从而进一步提高时延估计精度。
