基于扩展路径识别算法的水声OFDM系统低复杂度迭代稀疏信道估计

赵世铎 鄢社锋

(中国科学院声学研究所 北京 100190)

(中国科学院大学 北京 100049)

1 引言

在移动OFDM水声通信中，收发机的相对运动会引起多普勒效应，从而破坏OFDM系统子载波之间的正交性，带来子载波间干扰(Inter-Carrier Interference, ICI)。传统的水声OFDM系统通常假设接收机在进行多普勒估计及补偿后可以近似认为接收信号中无ICI，进而采用频域单抽头信道模型进行信道估计[1–4]。但是，在移动水声通信中，由于多普勒估计误差的存在，接收端对多普勒进行补偿后仍然会存在1 ×10−4数量级的残余多普勒因子[5]，若不对其进行有效处理将严重影响系统的性能。

为了提高移动OFDM水声通信系统的性能，研究者提出了基于压缩感知算法(Basis Pursuit, BP),OMP (Orthogonal Matching Pursuit)及其改进算法[6]等的信道估计方法[7–10]。该类方法采用基于多径参数的时变信道模型，利用信道在时延-多普勒2维平面上的稀疏性，构建字典矩阵，然后采用基于凸优化或迭代追踪的方法精确估计各多径的多普勒、时延及幅度参数。由于将多普勒纳入信道模型，该类方法可以获得更加准确的信道估计，从而降低系统误码率。但是，一方面，为了获得高精度信道估计，该类方法需要在更加细化的时延和多普勒网格上构造字典；另一方面，在大时延扩展的信道中需要增加时延网格的覆盖范围，这些都将增加算法的计算复杂度。特别是在Turbo接收机及MIMOOFDM系统等一次传输需要进行多次信道估计的场合，有时该类算法的计算复杂度会不可接受，这限制了其在实时通信中的应用。

针对这一问题，研究者近年提出了一种快速稀疏信道估计算法，即路径识别(Path Identification,PI)算法[11]。该方法通过利用时延导向向量相关函数的先验知识，将算法的计算复杂度与字典的时延分辨率和时延覆盖范围独立开来，从而能够以极低的计算量实现稀疏信道估计。但是，该方法并没有考虑信道的多普勒效应，故不适用于移动OFDM水声通信。针对这一问题，本文提出一种适用于一致多普勒信道的扩展路径识别(Generalized PI, GPI)算法，并将传统PI算法作为其在无多普勒环境下的特例。该方法在接收端首先使用多普勒扩展矩阵构建等效发射序列，将一致多普勒信道转化为等效线性时不变(Linear Time Invariant, LTI)信道；接着用GPI算法估计信道多普勒及各路径的时延和幅度参数，实现低复杂度稀疏信道估计。此外，本文将GPI算法扩展到Turbo接收机中，利用上次迭代获得的数据符号先验信息迭代提高信道估计精度，并减少所需导频数量。仿真结果表明，GPI算法的性能优于传统的PI算法，并且接近OMP算法，而其计算量比后者降低了一个数量级。

2 系统模型

2.1 OFDM系统模型

2.2 水声信道模型

3 迭代稀疏信道估计

3.1 扩展路径识别算法

一致多普勒水声信道下的接收OFDM信号可写为

其中，

3.2 Turbo迭代信道估计

虽然上述推导中假设所有子载波上的符号均已知，但在实际中一般仅导频子载波上的符号已知，而数据子载波上的符号是未知的。在这种情况下，想要准确估计多普勒信道需要大量导频[7,8]，这将降低系统的带宽效率。Turbo迭代信道估计可以利用上次迭代得到的数据符号先验信息辅助信道估计，从而提高信道估计精度，并减小所需的导频数量[12,15]。

在初次迭代中，仅使用导频符号执行GPI算法。获得各路径参数的估计值后，使用式(8)重建频域信道矩阵，然后根据式(7)的模型采用如MMSE或SDFE[12,16]等软输入软输出(Soft-Input Soft-Output, SISO)均衡器估计数据符号并将结果送入SISO信道译码器进行译码。译码器输出各符号的比特软信息，并转化为数据符号的先验均值和方差[17]反馈给信道估计器和均衡器。在后续迭代中，GPI算法同时使用导频符号和反馈的数据符号先验均值进行信道估计，获得更加准确的估计结果。图1给出了基于GPI算法的Turbo接收机流程图。

图1 基于GPI算法的Turbo接收机流程图

3.3 复杂度分析

假设 K个子载波均用于信道估计，并记集合Ω 和 Γ 中的元素个数分别为Nb和Nτ。分析GPI算法和基于压缩感知的OMP算法的复数乘法(Complex Multiplication, CM)次数复杂度。

GPI算法的复杂度主要由3个部分组成：构建等效发射符号序列需要NbK2次CM；求解式(18)需要NbNτK次CM；求解PI算法步骤4中的最小二乘需要 P3数量级的CM。故GPI算法总共需要约NbNτK+NbK2+P3次CM操作。

4 仿真结果

仿真采用ZP-OFDM水声通信系统，其参数如表1所示。

其中，1024个子载波中包含672个数据子载波，256个导频子载波和96个空子载波[1,8,12]。导频采用均匀分布，即导频子载波序号为4m,m=0,1,···,255。

表1 OFDM水声通信系统仿真参数

仿真中采用基于多径参数的水声信道模型[8,12,16]。相邻路径之间的时延差服从均值为1 ms的指数分布；各路径幅度服从瑞利分布，且平均功率随时延指数衰减；信道多普勒因子服从最大值为bmax的零均值均匀分布。注意这里的信道多普勒因子模拟的就是多普勒补偿后的残余多普勒因子，故仿真中不进行图1中的多普勒粗估计与补偿。仿真中采用MMSE均衡器，并假设各子载波上的ICI主要来自其左右各 D 个子载波[12,16](仿真中固定D =3)。子载波符号调制方式采用QPSK，信道编码采用码率为1 /2的二进制LDPC码。

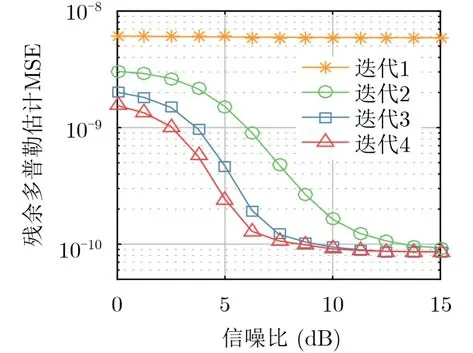
图2 b max =1.5×10−4时GPI算法的残余多普勒估计MSE与信噪比关系

注意到，初次迭代的多普勒估计误差几乎不随信噪比变化，这是因为均匀分布的导频无法有效获取相邻子载波上的ICI信息[8]，而该问题是不会随着信噪比的增加而改善的。随着迭代的进行，GPI算法的残余多普勒估计误差逐渐减小，并且在后续迭代中，由于使用全部子载波符号估计信道，多普勒估计误差会随着信噪比的增加而明显改善。另外，由于对多普勒搜索范围进行了离散化，在高信噪比区域存在误差平台。

接下来仿真传统单抽头信道估计[1]，PI[11], GPI以及OMP[8]这4种算法的解码后误码率(Bit Error Rate, BER)随信噪比(Signal-to-Noise Ratio,SNR)变化的曲线，其中对PI, GPI和OMP算法均采用Turbo迭代信道估计，仿真结果见图3。

可见，由于ICI的存在，单抽头信道估计性能最差；GPI和OMP算法初次迭代的误码率仅略微优于PI算法，这是因为均匀分布的导频无法有效获取相邻子载波上的ICI信息[8]；注意到，虽然GPI算法初次迭代的多普勒估计误差基本不随信噪比增大而改变(见图2)，但由于对多径时延和幅度的估计精度会随信噪比增加而提高，故GPI算法初次迭代的误码率会随信噪比增大而降低；随着迭代进行，由于可以使用数据符号的先验信息估计信道，PI, GPI和OMP算法的性能均有提高，但是，由于PI算法没有考虑信道多普勒，其性能随迭代的提高并不明显；另外，相同迭代次数下，本文提出的GPI算法相比于OMP算法仅有0.5～1 dB的性能差距。

接下来固定 SNR=8 dB，仿真各信道估计算法的BER随bmax变化的曲线，仿真结果见图4(由于基于PI算法的Turbo接收机性能随迭代无明显增加，故这里仅展示其初次迭代的结果)。可见，当bmax=0 时，由于Ω ={0}，GPI算法的初次迭代退化为PI算法，故二者性能相同；随着 bmax增大，PI算法的性能显著下降，而GPI和OMP算法随着迭代的进行，即使在大多普勒信道下依然能获得较好的性能。

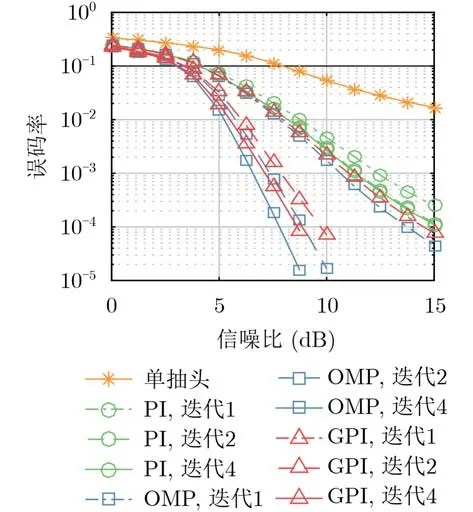
图3 b max =1.5×10−4时各信道估计算法的误码率与信噪比关系

最后，图5给出了GPI和OMP算法所需的CPU运行时间随路径数目 P变化的曲线。可见，由于初次迭代仅使用导频符号估计信道而后续迭代采用全部符号，故两种算法后续迭代的计算时间均大于初次迭代。另外，本文提出的GPI算法的运行时间比OMP算法降低了一个数量级左右，且二者间的差异随路径数增大而增大，这与3.3节的分析吻合。

5 结束语

本文提出一种一致多普勒水声信道下的低复杂度稀疏信道估计算法。算法首先使用信道多普勒扩展矩阵构造等效发射序列，将多普勒信道转化为等效LTI信道；然后使用GPI算法估计稀疏信道各路径的多普勒、时延及幅度信息。另外，所提方法被扩展至Turbo接收机中，通过利用译码器反馈的数据符号先验信息迭代提高估计精度。仿真结果表明，提出方法误码率优于传统路径识别算法，并接近OMP算法，而计算复杂度比OMP算法显著降低。

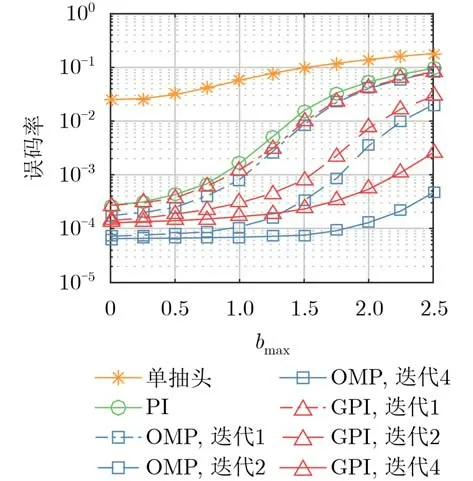
图4 S NR=8 dB时各信道估计算法的误码率与b max(×10–4)关系

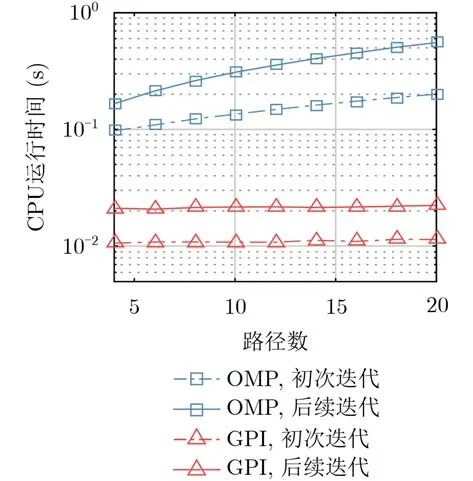
图5 GPI和OMP信道估计的CPU运行时间比较