基于DOA-TDOA-FDOA的单站无源相干定位代数解

黄东华 赵勇胜 赵拥军 储美娟

(中国人民解放军战略支援部队信息工程大学 郑州 450001)

1 引言

基于外辐射源的无源定位方法又称无源相干定位(Passive Coherent Location, PCL)技术，其特点在于自身不辐射电磁波，而是利用环境中已有的第三方辐射源(如调频广播信号[1]、数字电视信号[2]、雷达辐射源信号[3]、WiFi信号[4]、卫星信号[5,6]等)来探测和定位目标。这一特殊的工作原理，使其相比于有源雷达系统具有体积小、成本低、隐蔽性高、不占用频谱资源等优点[7]。相比于多站系统，单站系统不存在时间和数据同步的问题，机动性好。因此，研究高精度的单站外辐射源定位方法具有重要的意义。

无源相干定位系统的明显特征是其观测站上配置了两条接收通道，其中一条为参考通道，用于接收来自外辐射源的直达波信号，另一条为监视通道，用于接收潜在的目标回波信号[8]。对于无源相干定位问题，有直接定位和两步定位两种思路。直接定位利用目标回波信号的时频特性等从接收信号中直接估计出目标位置参数，避免了定位参数提取引入的误差，但是直接定位方法计算量过大的缺点限制了其在实际中的应用。两步定位首先从接收信号中提取出目标回波信号到达接收站的角度(Direction Of Arrival, DOA)、时差(Time Difference Of Arrival, TDOA)、频差(Frequency Difference Of Arrival, FDOA)等定位参数[9–11]，然后通过设计合理的定位算法，从DOA, TDOA和FDOA等定位参数中估计出目标的位置和速度等信息。然而，由于DOA, TDOA和FDOA观测方程与目标位置参数之间存在高度非线性的函数关系，因此，基于DOA,TDOA和FDOA的单站无源相干定位问题并不容易。

目前，学术界对于单站无源相干定位问题的研究主要可以分为基于TDOA的定位[12–17]、基于D O A 和T D O A 的 定 位[18–21]、基 于T D O A 和FDOA的定位[22–24]。基于TDOA的定位方法对时差观测精度要求较高，在时差估计精度较低时，算法的定位精度不甚理想。相比于基于TDOA的定位方法，基于DOA和TDOA的定位方法由于使用了额外的角度观测量，因此目标位置的估计精度也更高，但是缺点在于无法估计出目标速度信息。基于TDOA和FDOA的定位算法通过联合FDOA信息，可以同时估计出目标的位置和速度信息，但是对于目标位置的估计精度要低于基于DOA和TDOA的定位方法。相比于上述3种定位方式，联合DOA,TDOA和FDOA的定位方式理论上可以同时估计出目标的位置和速度信息，并且具有更高的估计精度。然而，目前对于联合DOA, TDOA和FDOA的无源相干定位问题，还缺少相应的定位算法。

为此，本文针对利用单个观测站接收多个外辐射源信号实现目标定位的问题，联合DOA, TDOA和FDOA观测，对目标位置和速度进行估计。将经典的两步加权最小二乘思想[25–27]应用到本文定位模型中，提出了一种适用于基于DOA, TDOA和FDOA观测的单站无源相干定位问题的代数解算法。推导了基于DOA, TDOA和FDOA观测的单站无源相干定位的CRLB。最后通过仿真实验验证了算法的有效性。

2 定位场景

联合式(3)和式(4)中的角度观测，式(9)中的时差观测，以及式(10)中的频差观测，得到系统整体的观测方程为

3 定位算法

本节推导角度、时差和频差观测的目标定位问题代数解，算法遵循经典的两步加权最小二乘框架。

3.1 第1步加权最小二乘估计

首先，利用三角函数和1阶泰勒级数展开，将式(3)和式(4)中方位角和俯仰角的观测方程转化为如式(12)和式(13)线性形式

将式(14)关于时间求导，从而得到目标位置参数与频差观测量之间的伪线性方程为

误差向量矩阵∆ h1可以表示为

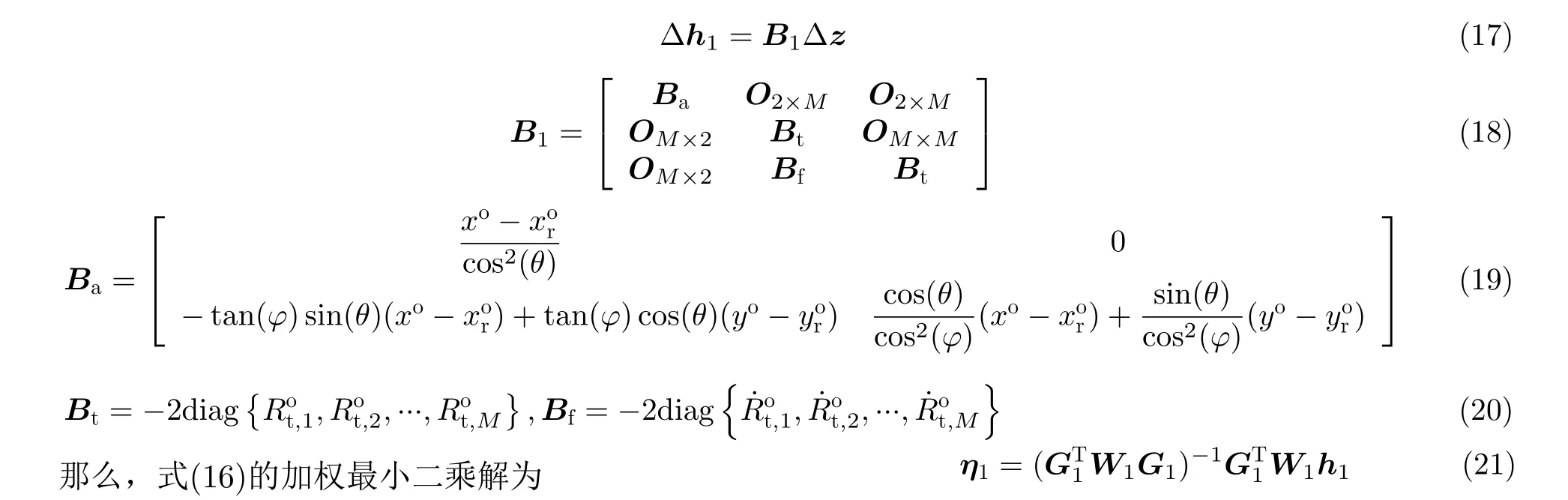
3.2 第2步加权最小二乘估计

4 CRLB及理论性能分析

4.1 CRLB分析

其中， κ为常数。根据式(35)中的概率密度函数，可得Fisher信息矩阵(Fisher Information Matrix,FIM)为

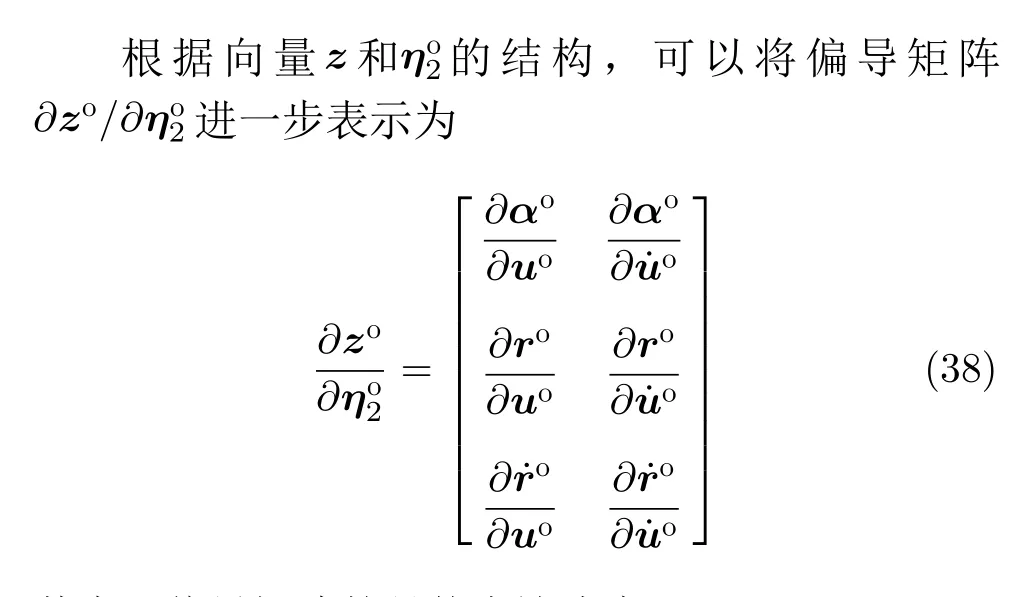
其中，偏导矩阵的具体表达式为

4.2 理论误差分析

因此，在观测误差较小时，本文算法的理论协方差矩阵与CRLB相等，即本文算法的定位误差可以达到CRLB。

5 仿真实验

本节通过仿真实验来评估算法的定位性能。仿真场景如下：观测站的位置为[ 0,0,0]Tm，速度为0；外辐射源数量M =4， 其位置分别为[ 2000,0,0]Tm,[0,2000,500]Tm ，[−2000,0,1000]Tm 和[0,−2000,

仿真1 CRLB比较

为了验证本文联合DOA-TDOA-FDOA定位方法相比于现有的TDOA定位、DOA-TDOA定位、TDOA-FDOA定位3种定位方式的优越性，在图1中绘制并比较了以上4种定位方式对目标位置和速度估计的CRLB。

从图1(a)可以看出，在位置估计方面，基于TDOA定位的位置估计精度与基于TDOA-FDOA定位相当。基于DOA-TDOA定位的位置估计精度显著优于基于TDOA定位以及基于TDOA-FDOA定位，但略逊于本文基于DOA-TDOA-FDOA定位。从图1(b)可以看出，在速度估计方面，基于TDOA定位和基于DOA-TDOA定位由于其观测量与目标速度之间不存在函数关系，因此无法估计出目标速度。与基于TDOA-FDOA定位相比，联合DOA观测后，基于DOA-TDOA-FDOA定位的速度估计精度有了显著提升。结合图1(a)和图1(b)，可以充分看出本文基于DOA-TDOA-FDOA定位方式相比于现有基于TDOA定位、基于DOA-TDOA定位以及基于TDOA-FDOA定位在定位精度方面的优越性。

仿真2 不同观测误差水平下算法定位精度分析

接下来，比较不同算法在不同观测误差水平下的定位性能。为了突出本文算法定位精度，给出了本文算法的均方根误差和偏差曲线，并将文献[16]中Chalise等人的算法(基于TDOA的定位算法)、文献[20]中Li等人的算法(基于DOA-TDOA的定位算法)、文献[22]中赵勇胜等人的算法(基于TDOA-FDOA的定位算法)对应的仿真结果也一并给出。仿真结果如图2所示。

图2给出了当系统的观测误差水平ρ 从–20 dB增加到50 dB时，上述4种定位算法的位置估计和速度估计均方根误差和偏差曲线。如图2(a)所示，在位置估计均方根误差方面，基于TDOA的定位算法与基于TDOA-FDOA的定位算法均方根误差曲线非常接近，而本文算法的位置估计均方根误差曲线与基于DOA-TDOA定位算法非常接近，并且在不同观测误差下的位置估计均方根误差均显著低于基于TDOA的定位算法与基于TDOA-FDOA的定位算法。这说明了DOA观测对于位置估计精度有着显著提升。此外，局部放大图进一步表明，严格来说本文算法定位精度要略高于基于DOA-TDOA定位算法，这说明FDOA观测对于位置估计精度有一定程度的改善，但是改善的程度很小。如图2(b)所示，在速度估计均方根误差方面，本文算法的速度估计精度要显著优于基于TDOA-FDOA的定位算法，这说明DOA观测的引入，对于速度估计精度有显著改进。因此，总体来看，与预期一致，在不同的观测误差水平下，本文算法的位置和速度估计均方根误差均低于其他几种定位算法，并且在观测误差水平较低( 20 lg(ρ)≤10dB)时，本文算法的定位均方根误差可以达到CRLB。虽然在观测误差较大时，本文算法的均方根误差曲线会逐渐偏离CRLB，但定位精度仍优于其余3种算法。本文算法偏离CRLB的原因均在于其算法推导过程中为了进行线性化处理，而忽略了2阶误差项。图2(c)和图2(d)分别给出了算法对于目标位置和速度估计的偏差曲线。由于定位问题的非线性，几种算法对目标位置和速度估计的偏差均随着观测误差的增大而增大，但相对来说，本文算法的偏差较小。

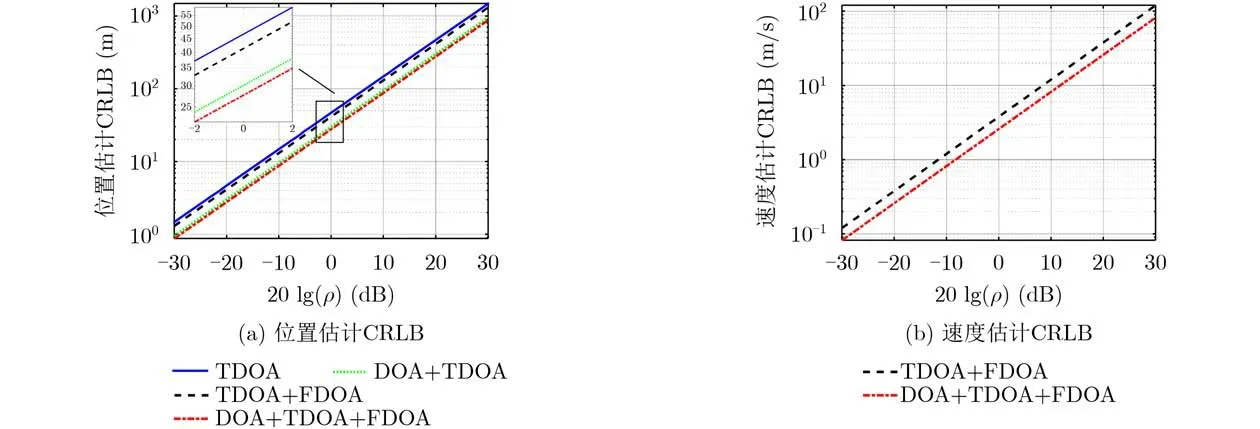
图1 不同观测误差水平下不同定位方式的CRLB比较

图2 不同观测误差水平下算法的定位精度

仿真3 不同位置下算法的定位精度分析

接下来，分析目标所在位置的不同对算法定位误差的影响。假设目标初始位置为[ −3000,0,300]Tm，以速度为[ 300,0,0]Tm/s沿着x轴运动。观测误差水平设置为 σa=0.1◦, σt=100m , σf=1m/s。观测站和接收站的位置与速度保持不变。不同算法对目标的定位误差精度如图3所示。

图3给出了不同位置下算法对目标位置和速度估计的均方根误差和偏差。可以看出，总体上，在不同的目标位置下，本文算法的均方根误差和偏差依旧低于现有几种定位算法。比较图3(a)中不同位置下算法的位置估计均方根误差可以看出，总体上，随着目标x坐标接近观测站，算法的位置估计均方根误差逐渐减小。值得注意的是，在目标x坐标接近观测站时，本文算法的定位均方根误差出现了偏离CRLB的现象，造成这一现象的原因在于同样的观测误差下，当目标x坐标接近观测站时，相对观测误差(观测误差与目标到观测站距离之比)会增大，从而造成算法定位误差偏离CRLB。此外，当目标x坐标为0时，算法的位置和速度估计误差低于CRLB。结合图3(c)和图3(d)中不同位置下算法的估计偏差情况可以看出，本文算法在目标x坐标为0时，会出现偏差增大的情况。因此，造成算法估计均方根误差在目标x坐标为0时低于CRLB的原因是，当相对观测误差较大时，算法给出的估计为有偏估计，而对于有偏估计来说，其算法的定位误差可以低于CRLB。

6 结束语

DOA, TDOA和FDOA是无源相干定位系统目标检测和参数估计环节产生的基本参数。本文联合DOA, TDOA和FDOA观测，对目标位置和速度进行估计，提出了一种代数解定位算法。算法遵循两步加权最小二乘基本框架：第1步通过引入辅助参数，将非线性的观测方程转化为伪线性方程，从中得到目标位置和速度的粗估计；第2步通过利用辅助参数和目标位置参数之间的约束关系来提高估计精度。分析了算法的理论误差，并将其与推导的CRLB进行比较。仿真实验验证了算法的有效性和优越性。此外，本文算法假设外辐射源位置和速度均准确已知，但实际中外辐射位置和速度通常存在一定误差，特别是当外辐射源为高度非合作的运动辐射源。针对此问题，理论上可以通过利用外辐射源位置和速度误差统计特性[27]，或者利用位置和速度已知的合作目标[28]，来降低外辐射源位置和速度误差对目标定位精度的影响，这将是以后进一步的研究方向。

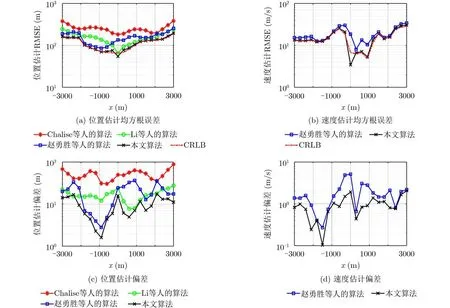
图3 不同位置下算法的定位精度