基于稀疏贝叶斯学习的空间紧邻信号DOA估计算法
2021-04-06王琦森陈焱琨
王琦森 余 华 李 杰 董 超 季 飞 陈焱琨
①(华南理工大学土木与交通学院 广州 510640)
②(自然资源部海洋环境探测技术与应用重点实验室 广州 510300)
③(华南理工大学电子与信息学院 广州 510640)
④(国家海洋局南海调查技术中心 广州 510300)
1 引言
波达方向(Direction-Of-Arrival, DOA)估计,广泛应用于声呐、雷达和无线通信等许多领域[1]。经过几十年的发展,出现了有超分辨能力的子空间类方法, 如MUSIC[2]等。然而在低信噪比等环境中,这类算法的性能会明显降低。
近年来的稀疏重构类算法克服了子空间类方法的缺点。 ℓp范数法是经典的稀疏类方法之一,其代表是ℓ1范 数。文献[3]首次把DOA估计转化为ℓ1范数问题,提出了奇异值分解的L1范数重构算法(L1 reconstruction-Singular Value Decomposition, L1-SVD),并利用网格细分法来提升精度。然而 ℓp范数类算法对信号的重构并不准确[4],其正则化因子难以确定,网格细分策略会使得基之间的相关性增强而导致性能的降低[3]。
稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)算法最初作为机器学习在文献[5]中提出,随后被引入稀疏信号处理领域[4,6],表明了SBL相对于ℓp范数法具有更好的重构性能。文献[7]把SBL用于DOA估计,提出了相关向量机方法(Relevance Vector Machine, RVM),该方法利用期望最大化(Expectation Maximization, EM)对信号后验概率密度函数进行最大化来完成信号空间功率的估计,并提出了一种后处理高精度算法来实现离格(offgrid)DOA估计,相比网格细分方法提高了计算效率和精度。文献[8]用泰勒展开把离格DOA误差引入阵列流形矩阵,提出离格稀疏贝叶斯推断 (Off-Grid Sparse Bayesian Inference, OGSBI),能在稀疏的网格下实现较准确的估计;文献[9,10]使用了一种线性插值方法进行离格DOA建模,其效果和文献[8]类似;文献[11]基于文献[8]的泰勒展开模型提出了网格自适应方法,使用分布式传感器对室内近场信号进行2维定位;文献[12,13]提出求根稀疏贝叶斯(root-Sparse Bayesian Learning, root-SBL),即基于SBL理论使用多项式求根法在每次迭代里解得离格误差,相比文献[8]提高了计算效率和对网格间距的稳健性。文献[14]把SBL应用于海洋匹配场处理进行声学探测。近年来,SBL还广泛应用于MIMO信道估计[15]、互质阵列[16]和宽带测向[17]。其中文献[16]使用变分贝叶斯(Variational Bayesian Inference, VBI),针对协方差向量使用泰勒展开模型进行离格DOA估计。
但是,对于空间紧邻信号的DOA,密集的网格点提高了算法的估计精度却增加计算负担,而稀疏的网格点减小了计算负担的同时以牺牲估计性能为代价。针对此问题,本文提出一种基于稀疏贝叶斯学习的空间紧邻DOA估计算法,包括3个步骤:(1)超参数的预估计;(2)网格插值优化和超参数的二次估计;(3)改进的离格DOA估计。第(1)步通过最大化阵列输出的边缘似然函数,推导了信号在拉普拉斯先验分布下的不动点迭代公式,相比其他SBL算法有着更快的收敛速度,并通过计算信号协方差矩阵的对角线元素而比其他SBL算法具有更低的计算复杂度;第(2)步使用最大似然方法2次估计噪声方差,并根据谱峰特征对网格点进行插值优化,在新网格点集的基础上2次估计信号功率;第(3)步推导了信号在拉普拉斯先验分布下的边缘似然函数关于角度的最大化公式以进行离格DOA搜索。仿真表明本文所提算法比其他经典SBL算法具有以下优势:(1)对空间紧邻信号的DOA具有更高的估计精度和分辨率;(2)低信噪比下的估计性能和计算效率更好;(3)可以使用大迭代门限取得更高的估计精度。
2 信号模型及稀疏表示
假设有 K 个远场窄带信号同时入射到具有 M个阵元的均匀线阵,定义方位角θ =[θ1,θ2,··· ,θK]为信号入射直线与阵列法线的夹角,则阵列在 t时刻的输出数据为
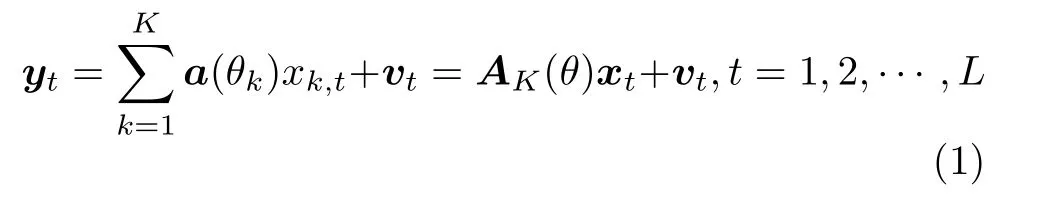
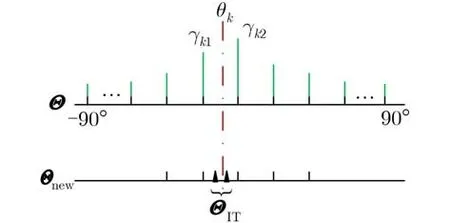
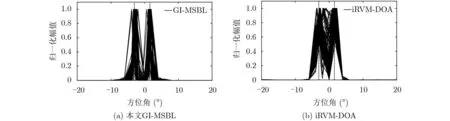
其 中, yt=[y1,t,y2,t,···,yM,t]T是 阵 列 接 收 数 据;xt=[x1,t,x2,t,···,xK,t]T是 K 个 信 号 在t 时 刻 的 波形; AK(θ)=[a(θ1),a(θ2),···,a(θK)] 是 K个信号的阵 列 流 形 矩 阵;a(θk)=[ej2πfτk,1,ej2πfτk,2,···,ej2πfτk,M]T是第k 个信号对应的阵列流形向量,其中f 是信号频率,τk,m=Dmsin θk/c 是第k 个信号在第m个阵元到参考阵元间的时延,c 是信号传播速度, Dm是 第m 个阵元到参考阵元的距离;vt是高斯白噪声向量,其方差为σ2。考虑把整个空域角度范围均匀划分成 N个网格点,每个网格点代表一个可 能 的 入 射 方 向,即 Θ =[ϑ1,ϑ2,···,ϑN],并 有K < 其中,过完备阵列流形矩阵A(Θ)=[a(ϑ1),a(ϑ2),···,a(ϑN)]∈CM×N可以简化为 A ,是稀疏向量,里大多数元素为0、只有少数元素不为0,中非0元素的位置代表信号的估计DOA,如果有 L个快拍,式(2)的单快拍模型就变为多快拍模型,即可以延伸为[3] 稀疏贝叶斯学习首先要建立促进稀疏的先验分布[4,5]。假设信号的各个元素相互独立,各列服从均值为0、方差为 γ =[γ1,γ2,···,γN]T的复高斯分布,则幅度的概率密度函数为 由贝叶斯原理可得源信号关于阵列接收数据的后验概率为 为了提高DOA估计的精度并降低计算复杂度,本文提出一种基于稀疏贝叶斯学习的DOA估计改进算法,主要包括3个步骤。首先是超参数的预估计,此部分利用不动点迭代算法的快速收敛特性预估信号的空间功率谱,并通过估计信号协方差矩阵的对角线元素而避免了估计整个协方差矩阵来降低计算复杂度;其次,根据上一步功率谱的谱峰特征进行网格点的插值优化,并对噪声方差和信号功率进行2次估计,从而提高对空间紧邻DOA的分辨能力;最后通过推导似然函数关于角度的最大化表达式来进行离格DOA搜索,进一步提升估计精度。 由于谱峰之间保留的网格点可能有重叠,所以Θnew网格点数的最大值为7 K。与文献[3]中提出的网格细分方法不同,本文方法进一步利用了SBL算法的功率谱峰包含两较大幅值的谱峰特征,且没有对网格进行多级细分。如图1所示,粗短线代表原始网格点,竖直点划线是第 k个信号的实际DOA,竖线代表能量幅值,三角形为插入的网格点,使用这样的网格点插值优化方法的好处在于:增强了2次估计后的空间谱对空间紧邻信号DOA的分辨率,同时提高了计算效率。 图1 网格点插值优化 随后进行噪声方差的2次估计,这是因为准确的噪声方差可以提供更好的稀疏重构效果[7]。由文献[7,18]可以得到最大似然方法的噪声方差估计 2次估计后仍然存在DOA和网格点的失配误差,这里参考文献[7]的高精度DOA估计。相比文献[7]的方法,改进之处是推导了拉普拉斯先验分布下的边缘似然函数关于角度的最大化表达式,保证性能的同时降低了计算量。 本文所提算法简称为网格插值-多快拍稀疏贝叶斯学习 (Grid Interpolation-Multiple snapshot Sparse Bayesian Learning, GI-MSBL),流程总结如下: 步骤 1 信号功率的预估计。 表1 算法的计算复杂度 两个独立等功率的随机信号DOA为–3.05°和1.57°,信噪比均取10 dB,进行150次随机试验,得到空间谱如图2 所示。图2 的点划线为真实DOA,实线为空间谱,为了清晰展示取–20°~20°的方位角范围。对GI-MSBL算法,结合式(21),在插入网格点集 ΘIT后 ,总的网格点集Θtotal等 于 原 始 网 格 点 集 Θ 与ΘIT取 并 集:Θtotal=Θ ∪ΘIT,记Θtotal包含的网格点数为Ntotal,注意Θnew是Θtotal的一个子集,把Θnew里网格点对应的信号空间功率值赋值给Θtotal里对应网格点处的功率,再把网格点集 Θtotal里除网格点集Θnew以外的信号功率置0,作图时,横坐标为 Ntotal个网格点Θtotal对应的方位角,纵坐标是归一化信号功率幅值,从而得到图2(a)的空间谱。从图2可以看出GIMSBL比iRVM-DOA的谱峰波动更小,这是因为网格优化插值方法以及超参数的2次估计增强了对紧邻DOA的分辨率。这里只选取iRVM-DOA进行对比 ,其余算法与之类似,受篇幅所限不在此一一列出。 图2 算法的空间谱对比 两个独立等功率的随机信号角度为(− 3+u)°和(3 +u )°,u 从角度范围[-GRI,GRI]内随机选取(避免固定角度的影响),信噪比从–6~20 dB变化,每个信噪比下做150次随机试验,结果见图3(a)。低信噪比下,GI-MSBL0和GI-MSBL的误差都小于其他算法,这是因为超参数的2次估计增强了低信噪比的稀疏恢复能力。GI-MSBL算法在高信噪比下精度更高,这是网格插值方法带来的性能提升。由于所提不动点迭代公式(17)具有很快的收敛速度,且不同于其他SBL算法估计整个信号协方差矩阵,所提算法只估计信号协方差矩阵的对角线元素,所以图3(b)的GI-MSBL方法有着优于其他SBL类方法的运算效率。 固定信噪比5 dB,两个独立信号的DOA分别为( −3+u )°和(3 +∆θ+u) °,DOA间隔∆ θ从3°到11°变化,每个∆ θ下做150次随机试验,见图4。图4(a)中,在间隔3.5°到5.5°的范围内,GI-MSBL误差最小 。图4(b)中GI-MSBL在∆ θ<4.5°时分辨概率最高。 信噪比固定为5 dB,迭代门限ε 从0.001到0.1变化,其余条件同5.2节,每个 ε下做150次随机试验,见图5。图5(a)中,所提算法在迭代门限较大时估计误差最小。图5(b)中根据表1的平均复数乘法次数来衡量计算复杂度,GI-MSBL0以及GI-MSB L平均复数乘法次数最少。 为了改进对空间紧邻信号DOA估计的精度和计算复杂度,本文提出一种基于网格插值的多快拍稀疏贝叶斯学习 (GI-MSBL) 算法,改进算法比其他经典的稀疏贝叶斯学习算法具有以下优势:(1)对空间紧邻DOA具有更好的估计效果;(2)低信噪比下估计性能更好,计算效率更高;(3)能使用大迭代门限取得更高的估计精度。另外,对于水下宽带信号,通过傅里叶变换在频域对每个频段即可以使用所提算法。 图3 不同信噪比下的估计性能和运算效率 图4 不同DOA间隔下的分辨能力比较 图5 不同迭代门限下的估计精度和计算复杂度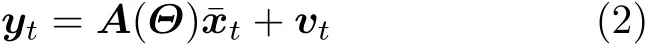


3 稀疏贝叶斯概率分布模型


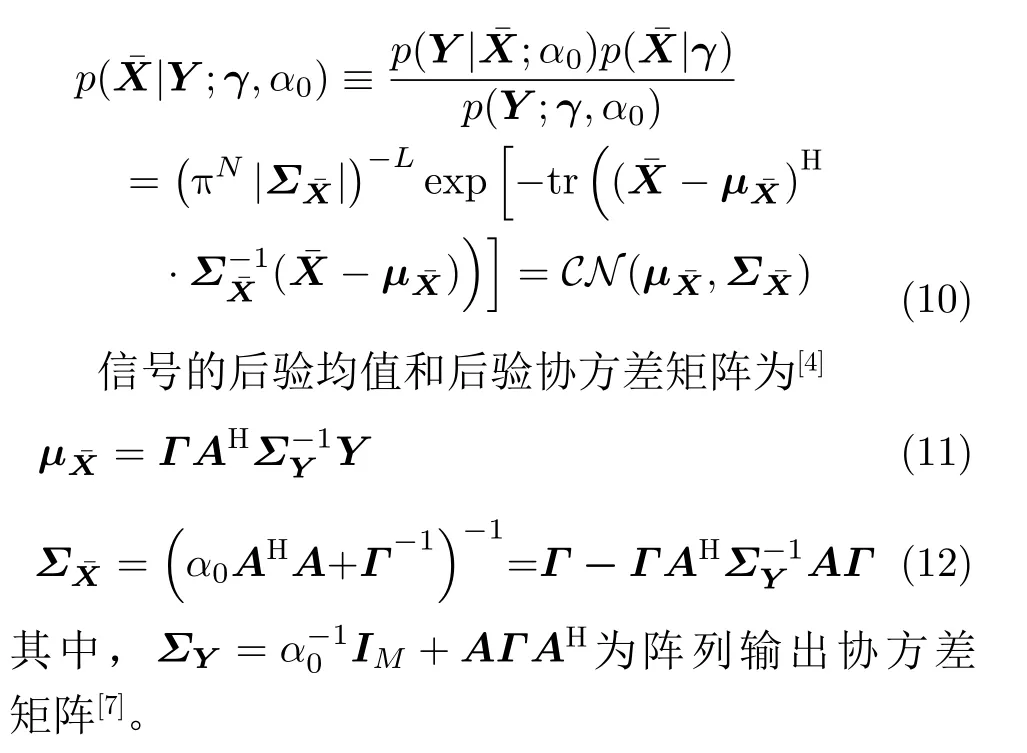
4 改进算法
4.1 超参数的预估计





4.2 网格插值优化及超参数2次估计

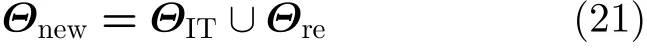
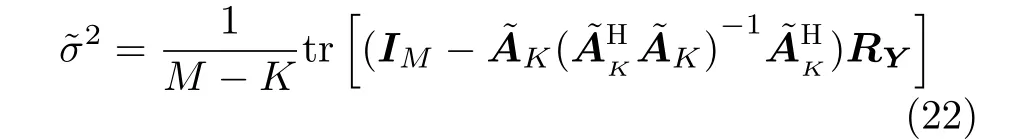

4.3 改进的离格DOA估计


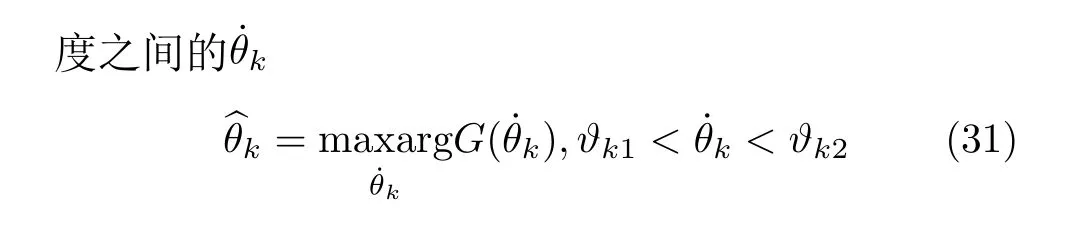
4.4 算法流程和运算复杂度分析

5 仿真分析
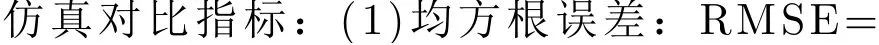



5.1 空间功率谱图对比
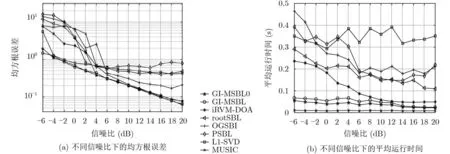
5.2 不同信噪比下的估计精度和运算效率比较
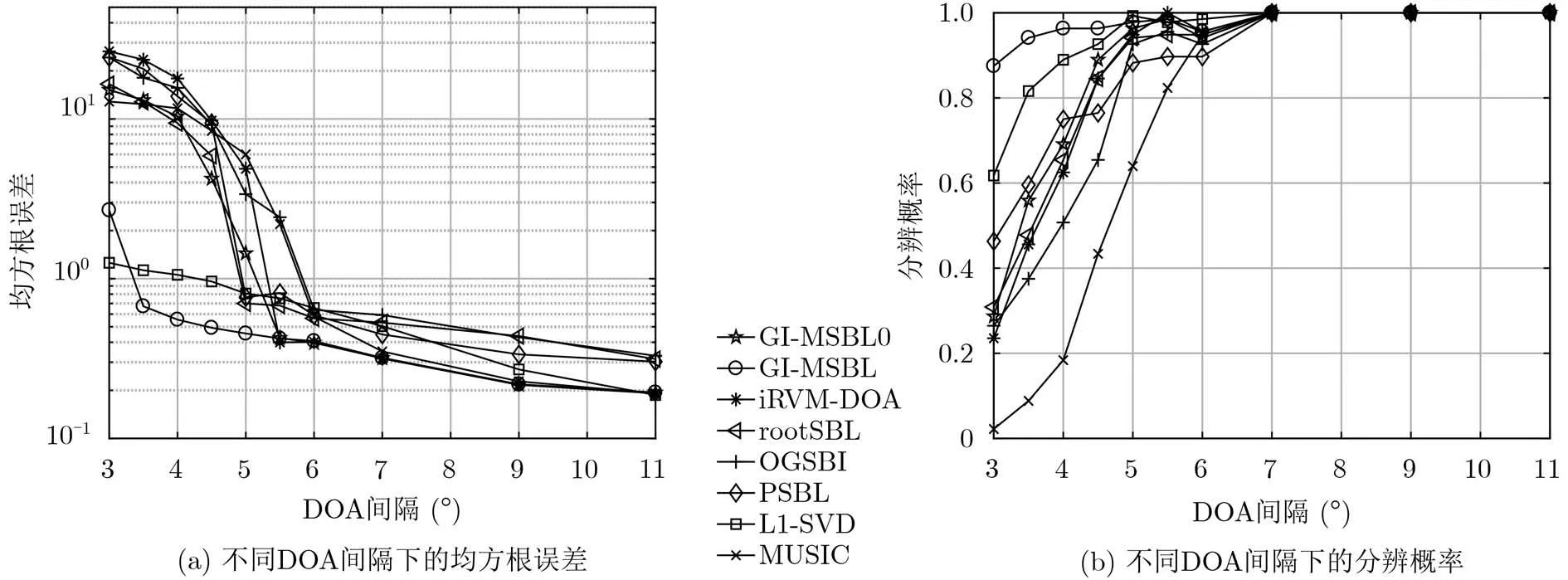
5.3 不同DOA间隔下的分辨能力比较
5.4 不同迭代门限下的估计精度和计算复杂度比较
6 结束语