弹道中段不同平动多目标的平动参数估计方法

冯存前 李 江 黄大荣 胡晓伟 韩立珣

(空军工程大学防空反导学院 西安 710051)

1 引言

近年来随着分导式多弹头及诱饵干扰等突防技术的发展[1]，基于传统特征的识别技术失效，战略预警和反导作战面临严峻考验，而微动特征作为目标固有运动属性为弹道目标识别提供了一种有效途径[2]。现有许多微动特征提取、参数估计及微动分类[3–7]的文献都是基于平动已得到较好补偿的前提下进行的，但群目标技术的发展使得弹道目标的平动补偿更为复杂，有待进行更深入的研究。

对于弹道中段目标的平动补偿方法国内外学者进行了广泛研究，大致可分为以下3种：(1)基于多普勒频谱信息。文献[8]提出了频谱重排法，对平动1阶加速度进行了估计，但此方法易受噪声影响；文献[9]提出一种分段平动补偿方法，通过使回波频谱熵最小化，在时频混叠的情况下有效地估计了加速度和速度。(2)基于时频分析。文献[10]利用目标的整体信息，采用Radon变换检测时频曲线倾斜度，结合最小熵准则和高斯模板函数对变换域进行峰值搜索实现平动参数估计。文献[11]通过改进的Harris角点检测算法提取出时频曲线的交点信息，完成平动参数估计进而实现平动补偿。但是此类方法在受到噪声严重污染时因无法进行图像特征的有效提取而性能急剧下降。(3)基于信号处理。文献[12]利用微多普勒信号的周期性进行延迟共轭相乘消除微动信号，然后等效为多项式相位信号参数估计问题实现平动2阶加速度和1阶加速度的估计；文献[13,14]则利用进动目标微多普勒信号的对称性，通过对称共轭相乘消除微动分量后进行傅里叶变换，搜索频谱峰值信息估计平动加速度和速度。此外还可通过构造冗余的微动原子集来估计平动速度和微动参数[15]，但仅适用于具有正弦形式的微动信号。

以上分析中，所采用的2阶多项式等效平动[8–11,13–15]的方法将会影响最后的补偿效果。此外，目前所进行的研究都是基于单目标或同一平动的群目标的情况，但对于更贴近实际的具有不同平动参数的多目标情况还没有相关方面的报道，因此有必要开展相关研究。

针对处理多目标问题，传统的思路都是先进行分离预处理，然后再进行参数估计，但此类方法过程繁琐且运算量大。本文考虑到弹道目标的平动补偿问题实际上是一个多项式参数估计过程，而高阶模糊函具有运算量小、估计阶数高及精度高等优势[16]，因此可应用于多目标平动补偿问题中；此外，考虑到周期信号进行延迟共轭相乘处理后，可在其频谱处出现峰值，而弹头目标的微动正是周期运动；最后，利用时频分布的差异进行时间维度的加权累加可实现速度估计。仿真结果验证了所提方法的有效性和低噪声条件下的鲁棒性。

2 复合运动模型

弹道群目标中，主要包括弹头、轻重诱饵、弹体碎片及燃料箱等，其中：燃料箱和碎片等可利用形态加以区别，因此本文将针对真假弹头组成的多目标进行平动分析研究。

2.1 回波模型分析

假设雷达发射波长为 λ的单频信号，则雷达接收到多目标的基频回波信号为

2.2 平动距离分析

首先利用观察时间内的某个脉冲测得速度 vi′对速度进行粗补偿[14]，可解决微多普勒时频图的折叠现象，补偿后的平动速度为∆ vi。同时在较短的观察时间内，平动分量可近似为3阶多项式[12]，则t 时刻粗补偿后的平动距离为

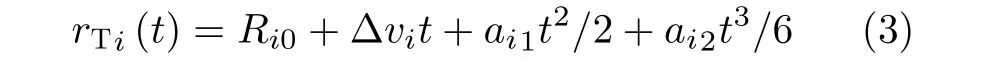
其中，Ri0, ai1, ai2分别为第i 个目标的初始径向距离 、1阶加速度、2阶加速度。

2.3 微动距离分析

由暗室测量实验知，弹道进动锥体目标其后向散射主要由锥顶 A和锥底滑动散射中心 B, C决定，如图1所示，其中：O −XY Z是与雷达坐标系平行的参考坐标， O −xyz为目标本地坐标系，原点O为目标质心，O x为目标对称轴。在图1(a)的锥体弹头进动模型中，对称轴O x 与锥旋轴O Z的夹角为进动角 θ ，且O x 轴初始时刻在O xy平面的投影与OX 轴的夹角为初始锥旋角φ0，记初始时刻雷达视线方向L OS与O Y Z 共面，且与锥旋轴O Z、对称轴Ox 的夹角分别为α, β。

由图1(a)可知，进动目标各散射点的微动距离为

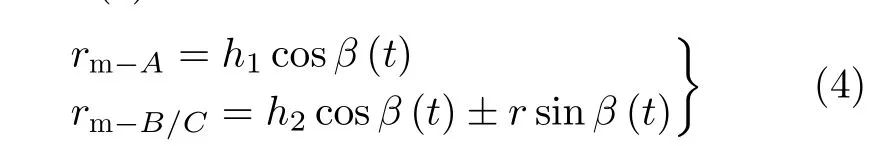
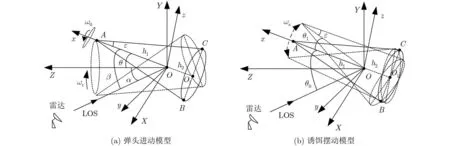
图1 微动模型

3 多目标平动参数估计方法

3.1 基于高阶模糊函数的2阶加速度及微动周期估计

回波的3阶矩函数可表示为

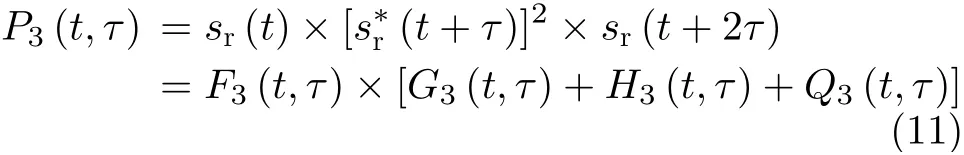
其中，

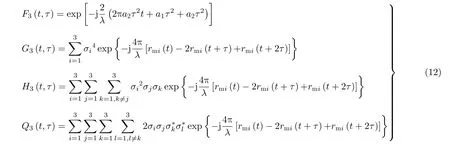
3.2 基于延迟共轭相乘的1阶加速度估计

交叉项在频域能量分散，对局部峰值位置影响不大。同理，对式(16)进行傅里叶变换，其余项频域能量分散，频谱峰值保持位置不变，即在多目标多散射点的情况下，其频谱仅是对应噪声基底增加，但局部峰值仍然明显。

3.3 基于时频分布的平动速度补偿

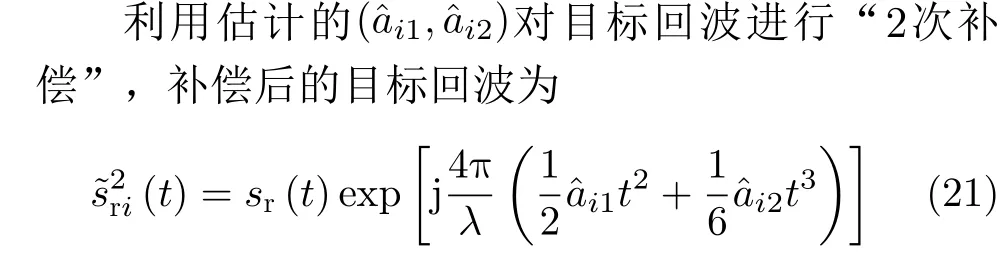
在补偿后的i ×j条目标回波时频图曲线中，将会表现为某一目标散射点对应的 j 条曲线被“拉平”，而其它目标散射点对应的曲线将会有不同程度的倾斜；被“拉平”的j 条曲线一个周期内存在两个能量较大的交点，且交点处曲线趋势变化快。

基于以上分析，我们将补偿后的回波时频曲线沿着时间横坐标进行累加处理。但由于时频曲线中存在其它能量强点，如：该 j条曲线的极值点位置附近的点、其它时频曲线的交点，这些点的存在将会对直接累加后的效果产生干扰。在整个观察周期内：该 j条曲线交点处所对应的这一行时频矩阵，具有多个能量强点，且交点处曲线斜率更大，使得能量强点的持续时间短。相比之下，其它曲线交点仅是个别强点；单曲线极值点位置附近的点能量相对较低，且曲线平缓，强点持续时间更长。即j 条曲线交点所对应位置处的时频矩阵数据，因具有多个持续时间短的能量强点，将会在其频谱上表现为：在更多的分频通道上分布能量较大的点。因此，将不同分频通道上的能量进行累加，该交点所对应的纵坐标处会出现最大值，从而实现对第i 个目标的平动速度的估计。具体操作如下：

4 仿真分析

为验证本文方法的有效性，进行如下仿真。设锥体参数为：质心到锥顶、锥底的距离分别为h1=1.125 m, h2=0.375 m ，底面半径r =0.252 m，目标散射数据由物理光学法获得。微动参数为：进动时，进 动 角 θ =10◦，锥 旋 角 速 度ωc=6 rad/s，初始锥旋角 φ0=10◦，雷达视线与锥旋轴α =45◦；摆动时，摆动角幅度 θ1=10◦，初始摆动角θ0=30◦， 摆动角速度ωs=8 rad/s。雷达参数：发射载频 f0=10 GHz ，脉冲重复频率P RF=1 kHz，观察时间T =4 s ，信噪比为5 dB，考虑遮挡效应。

设雷达目标回波中包含1个锥体弹头和1个锥体诱饵，目标平动参数为：弹头， ∆v1=−4 m/s,a11=1.5 m/s2, a12=0.5 m/s3； 诱饵∆ v2=−1.5 m/s,a21=0.8 m/s2, a22=0.25 m/s3。图2(a)为雷达目标回波的时频图，图2(b)为目标回波的3阶模糊函数，可得到明显的两个独立峰值。考虑到弹头的进动周期明显比诱饵的摆动周期长，因此可在“峰值搜索-去除峰值”过程中，以第1个目标“主峰值”为圆心，以∆ r′为半径，将此圆范围内的点进行置零处理。设置搜索的时间步长为 ∆t′=2/PRF,∆r′=50(局部峰值数量)。

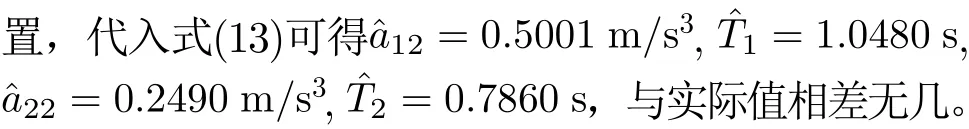
需要说明的是，模糊函数的时间搜索步长∆τ对参数的估计影响较大，原因在于当被估计周期不是 ∆τ的整数倍时，该周期处的峰值将会被搜索“跳过”，从而产生较大误差。本文经过多次仿真实验表明：仿真时间相差不大的前提下只要保持∆τ ≤0.004 s，估计参数仍然有效。因此可以选择较小的∆ τ 来减小估计误差，本文选取∆ τ =2/PRF。

接下来，我们对不同信噪比条件下参数估计的效果进行100次蒙特卡洛仿真。定义其归一化均方根误差(Normalized Root Mean Square Error,NRMES)为

图2 目标混合回波

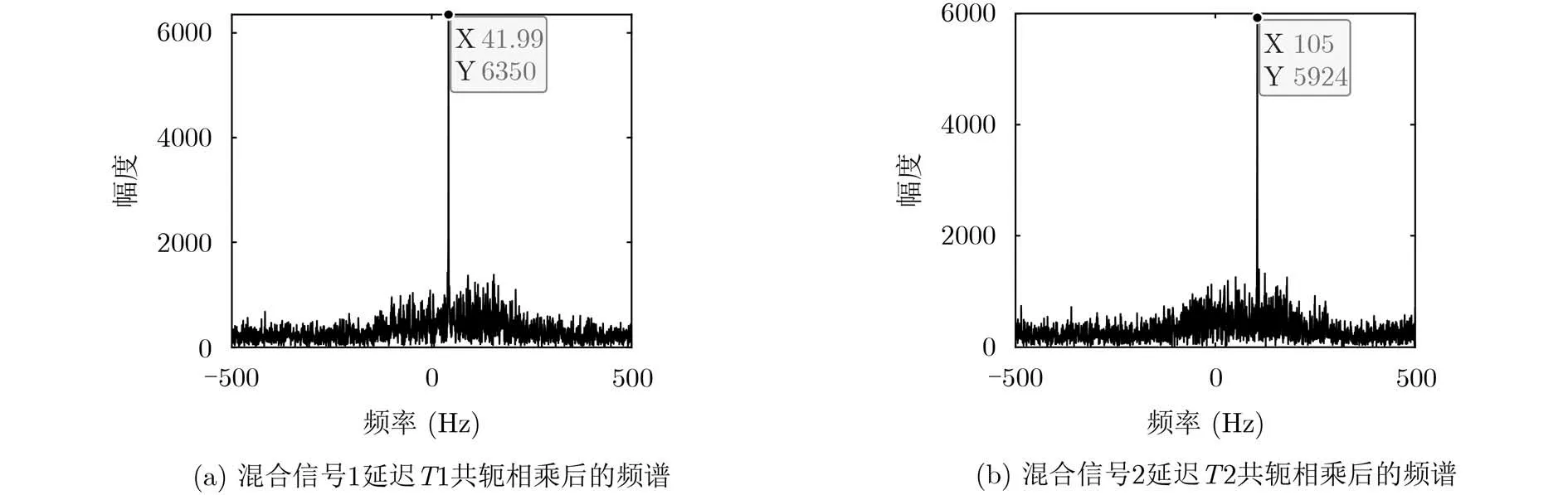
图3 延迟共轭相乘后的频谱图

不同参数在不同信噪比条件下的NRMES如图5所示。分析知，当信噪比不低于3 dB时，平动参数能够实现有效估计；当信噪比低于3 dB时，由于噪声干扰增大，一个目标的峰值搜索出现较大误差，但另一个目标仍能实现有效估计；由于其它时频曲线交点的干扰，目标的平动速度估计误差相对较大。

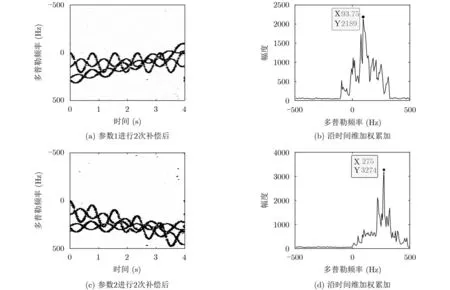
图4 剩余平动速度估计

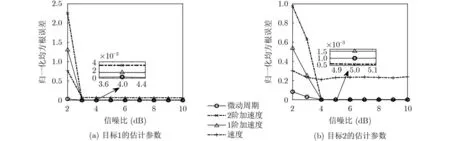
图5 参数估计值的蒙特卡洛仿真

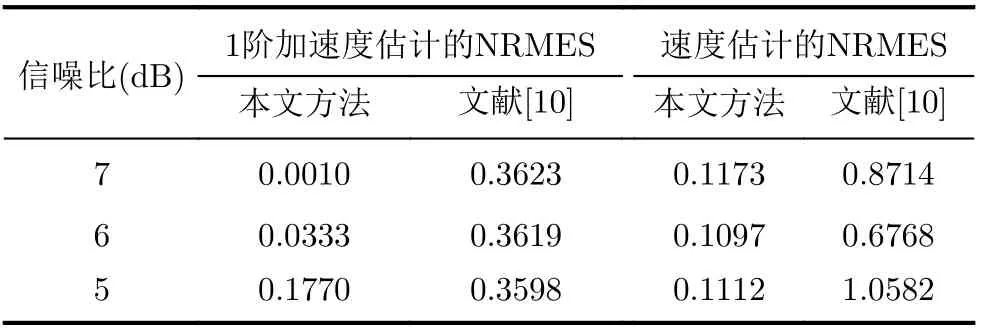
表1 多目标同平动参数的估计性能

为进一步验证本文方法的有效性，分别与文献[10,11]进行多目标、单目标同平动参数估计对比，表1，表2给出100次蒙特卡罗仿真的对比结果，图6—图8为其使用方法。

由表1，表2知，与文献[10,11]相比本文方法精度更高，分析如下：(1)与文献[10]相比，Radon变化仅能对整体时频图趋势进行直线拟合，这与实际曲线产生较大误差，而本文方法采用高阶多项式进行估计，因此精度更高；(2)与文献[11]比较，角点检测存在个别错误角点影响最终的拟合效果，并且当信噪比降低时角点检测错误率更高，而本文是利用信号延迟共轭相乘后自项能量高的特性，能更好地降低信噪比的影响，鲁棒性更强。

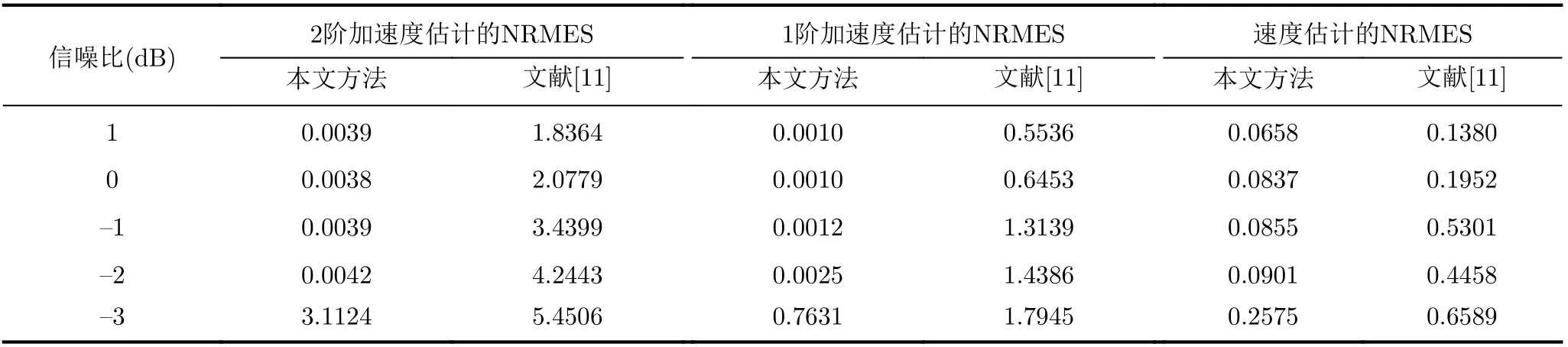
表2 单目标平动参数的估计性能

图6 文献[10]采用的Radon变换

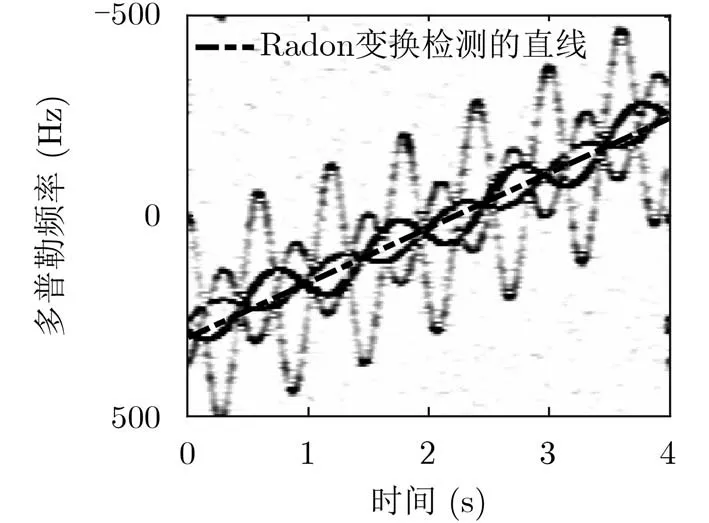
图7 文献[10]检测到的平动直线

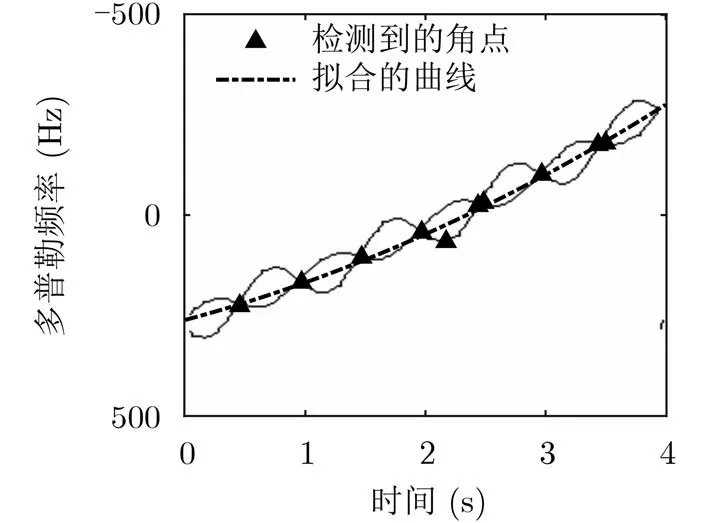
图8 文献[11]检测到的角点和拟合曲线

5 结束语

多目标雷达回波信号是多个分量的叠加，想要直接分离比较困难。本文采用高阶模糊函数通过峰值搜索完成逐次估计，并结合时频分析，可在不分离信号的前提下直接实现平动参数和微动周期的高精度估计，为弹道目标的参数估计和识别提供重要基础。

本文方法实质上是利用了微动信号的周期性，通过延迟共轭相乘消除或降低微动的影响来估计平动参数，因此可用于分析两个以上的目标，为弹道群目标的平动补偿提供一种思路。但是，多目标回波信号的延迟共轭将会导致处理后的回波信噪比降低，致使噪声鲁棒性变弱，且更多的时频曲线交点也会影响平动速度估计的效果，这也将是下一步研究的重点。