基于角多普勒效应的自旋目标微动特征提取

李 瑞 李开明 张 群② 梁 佳 罗 迎②

①(空军工程大学信息与导航学院 西安 710077)

②(复旦大学波散射与遥感信息国家教育部重点实验室 上海 200433)

1 引言

轨道角动量(Orbital Angular Momentum,OAM)[1]作为电磁波的一个重要物理量，由于其理论上具有无限正交模态，这就为电磁波的使用提供了一个新的物理复用维度。利用轨道角动量对电磁波相位波前进行调制时，能够获得具有螺旋形相位波前的涡旋电磁波(vortex electromagnetic wave)。在其上加载所需的信息，可提高电磁波的信息传递和获取能力。因此，携带轨道角动量的涡旋电磁波在众多应用领域受到了广泛关注，尤其是无线通信[2–4]，雷达目标成像[5–10]，以及旋转多普勒检测[11–14]等。

目前，在旋转探测应用领域里，角多普勒效应(angular Doppler effect)，也称为旋转多普勒效应(rotational Doppler effect)[15,16]，与线多普勒效应(Linear Doppler effect)相比鲜为人知。2013年，Lavery等人[17]在《Science》上发表论文，解释了涡旋光束角多普勒效应的产生机理。在此基础上，国防科技大学的黎湘教授团队[14,18]在暗室实验中验证了微波波段涡旋电磁波的角多普勒效应。2018年，英国格拉斯哥大学的Gibson等人[19]在涡旋声场中同样验证了角多普勒效应。在这些研究工作中，光波、微波或声波均是垂直照射或近似垂直照射旋转圆盘，而对实际中的微动目标来说，目标上各散射点一般难以总是满足入射角很小的假设条件。最近，文献[20]研究了涡旋电磁波雷达的多普勒和微多普勒效应，并对线多普勒频移和角多普勒频移进行了分析，特别是分析了由自旋产生的角微多普勒效应，研究指出反映角微多普勒效应的角微多普勒频移表达形式是极其复杂的，因此，该文献仅针对两种特殊情况进行分析并估计了自旋频率和半径两个参数。然而，对于沿着雷达径向飞行的自旋弹丸、垂直雷达视线(Line Of Sight, LOS)方向行驶的车辆目标上的旋转车轮这类目标，目标在雷达径向上无微动分量，此情况文献[20]并未进行详细研究。因此，针对上述类别的自旋目标，在同时考虑目标平动和自旋的前提下，本文研究了角多普勒效应，并提出了一种基于角多普勒效应的涡旋电磁波雷达自旋目标微动特征提取方法，该方法与基于线多普勒效应的微动特征提取方法[21,22]相比，能够提取出垂直于LOS方向的微动分量参数，可有效提升雷达在特定场景下的目标识别能力。本文工作有助于涡旋电磁波雷达目标检测的发展，在目标分类和识别领域具有潜在应用前景。

本文的结构安排如下：第2节介绍了涡旋电磁波雷达回波信号形式，并分析了自旋目标角多普勒效应；第3节给出了通过构造相位补偿函数获得角多普勒频移，进而提取自旋目标微动特征的方法；第4节给出了仿真实验结果并验证了所提方法的有效性和分析的准确性；最后，第5节对本文进行了总结。

2 自旋目标角多普勒效应

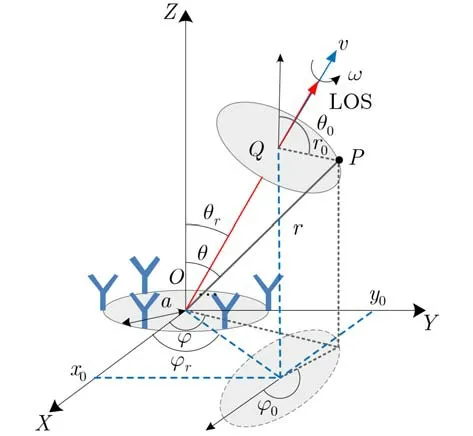
图1 UCA雷达和目标空间几何示意图

目前，有多种方法可以产生携带OAM的涡旋电磁波[23–26]。在雷达应用领域内，可以利用均匀圆环阵(Uniform Circular Arrays, UCA)产生携带有OAM的涡旋电磁波。如图1所示，UCA位于XOY平面上，产生携带OAM的涡旋电磁波，用 α表示。根据文献[27]，采用UCA接收到的散射点P 的回波信号可以表示为

为了方便对方位角变化进行分析，首先对点P的运动情况进行了简化。由于沿Z轴方向的运动不

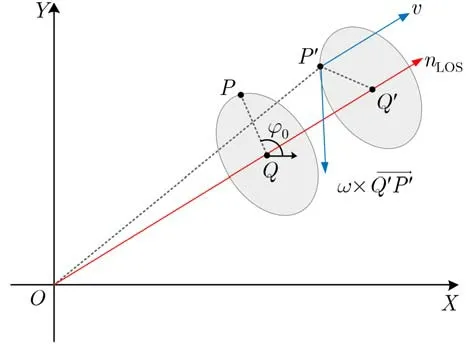
图2 点P平动和自旋运动等效几何示意图

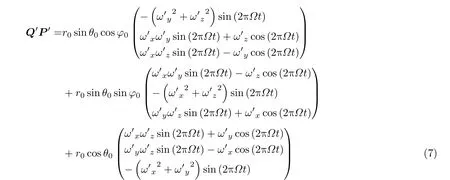
因此，可得

从式(4)和式(7)可以看出，点P 的平动和自旋均会产生角多普勒频移，其中由点P自旋运动产生的角多普勒频移可称作角微多普勒频移[20]，并且其形式较为复杂，并不是角多普勒频移和角微多普勒频移线性叠加形式。即使匀速运动参数作为先验信息已知，也很难构造相位补偿函数对匀速运动产生的角多普勒频移进行补偿。因此，将匀速运动和自旋运动产生的角多普勒频移整体考虑，得到了式(4)所示的自旋目标的角多普勒频移表达式。

尽管式(4)所示的角多普勒频移比较复杂，但根据角多普勒频移的物理意义，其产生是由于垂直于径向方向的运动引起的方位角变化。因此，通过分析匀速运动和自旋运动的几何关系，可推导出角多普勒频移的近似表达式，方便分析其与自旋参数的关系，提取自旋微动特征。

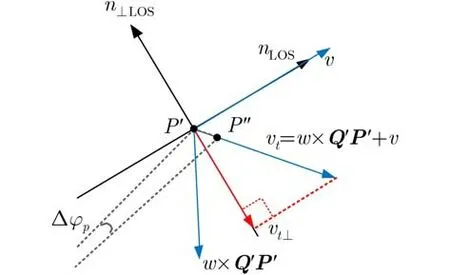
图3 在∆ t时间内，点P运动等效几何示意图

其中， θr为LOS方向与Z轴的夹角，β =arctan(tan θ0(nycos φ0−nxsin φ0))。根据式(13)可以得到下列结论：

(1) 角多普勒频移的大小与信号载频无关，而与OAM的模态有关。

(2) 线多普勒频移可以分解为平动引起的多普勒频移和微动引起的微多普勒频移的线性叠加形式，对角多普勒频移而言，平动和微动引起的多普勒频移和微多普勒频移相互耦合，无法分解成两部分的线性叠加形式。

(3) 角多普勒频移存在上确界和下确界，并且在上、下确界之间以 Ω的频率振荡，可以得到上、下确界的表达式分别为

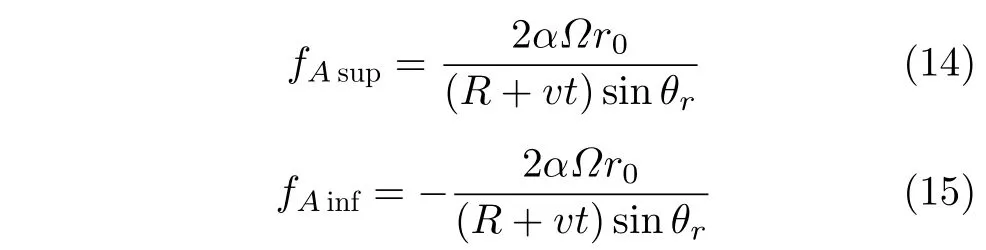
角多普勒频移的上、下确界由发射信号的OAM模态 α、目标平动速度大小v 、自旋频率 Ω、自旋半径 r0和LOS方向与Z轴的夹角θr确定。特别地，当平动分量为0时，自旋引起的角微多普勒频移与线微多普勒频移类似，其变化规律表现为正弦曲 线形式。

3 自旋目标微动特征提取

根据式(13)，通过分析角多普勒频移的变化规律，可以提取相应的参数信息。然而，由式(3)可知目标回波中存在目标平动和自旋引起的角多普勒频移，还存在目标平动引起的线多普勒频移。为此通过构造相位补偿函数来消除目标主体线多普勒频移。选取目标旋转中心Q作为参考点构造相位补偿函数

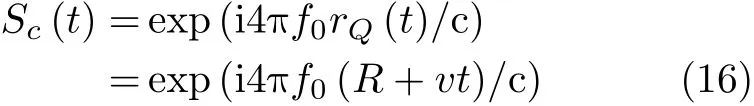
目标平动的速度估计可以采用现有成熟的算法，必要时可以通过发射辅助信号实现目标整体平动参数的准确估计。由于本文重点是提取目标微动特征，不妨假设目标平动速度大小 v已经被准确估计，构造出相位补偿函数 Sc(t)。将式(16)与式(2)相乘，可得补偿后的差频信号

综上所述，基于角多普勒效应的自旋目标微动特征提取方法的具体步骤如下：

步骤1 涡旋电磁波雷达的UCA发射携带OAM的涡旋电磁波对自旋目标进行探测；

步骤2 选取目标旋转中心Q作为参考点构造相位补偿函数对回波信号相位进行补偿，得到角多普勒频移曲线；

4 实验结果与分析

为了证明分析的准确性和所提微动特征提取方法的有效性，通过设计相应的仿真实验进行了验证，并对实验结果进行了分析。具体实验参数设置如表1所示。

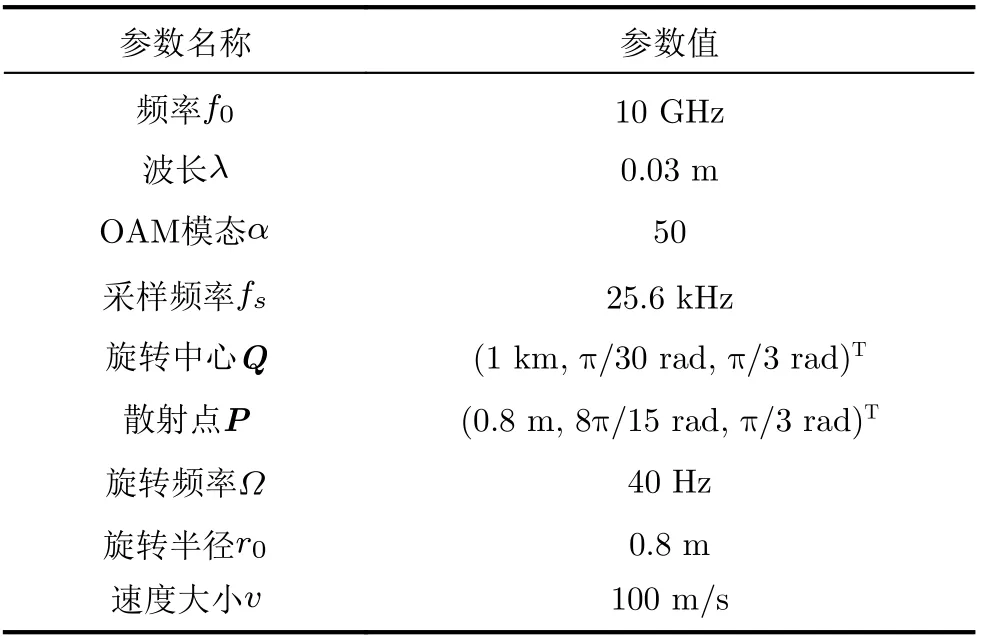
表1 相关参数设置

实验1 单散射点模型。考虑到在多散射点情况下，采用时频分析方法获得的频率估计精度有限，因此首先选用一个单散射点模型进行实验验证，这样能够采用对相位求导的方法来准确地计算出角多普勒频移，从而更好地验证本文的分析结论。

图4为传统平面波雷达经过平动补偿后得到的自旋引起的线多普勒效应(微多普勒效应本质上是由微动引起的多普勒效应，本文只做线、角多普勒效应的区分，故将线微多普勒效应也称作线多普勒效应)结果和涡旋电磁波雷达经过相位补偿后得到的平动与自旋引起的角多普勒效应结果，如图4(a)和图4(b)所示，当散射点沿LOS方向运动且自旋运动轨迹垂直于LOS方向时，自旋引起的线多普勒频移为0，因此现有的微动特征提取方法不再适用。此时，如图4(a)和图4(c)所示角多普勒频移仍然可以观测到，因此，基于角多普勒频移理论上可以提取微动特征。

如图5所示，图5(a)为观测时间0～1 s内的角多普勒频移曲线，而图5(b)为图5(a)中方框内局部放大的结果。通过理论分析得到的角多普勒频移理论值与观测值的对比图，其中实线为观测值，而虚线表示理论值。利用下列公式计算两条曲线之间的绝对误差

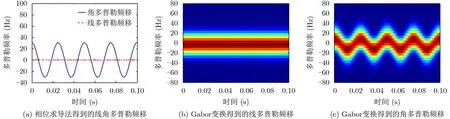
图4 线、角多普勒效应对比

如图6所示，实线表示相位干涉处理后得到的角多普勒频移曲线，虚线和点画线分别表示角多普勒频移的上确界和下确界，以上确界为例，测得上确界与角多普勒曲线的第4个交点坐标(0.075 s,30.16 Hz)和第34个交点坐标(0.825 s, 28.08 Hz)，将它们代入式(18)中的方程组，最终求解得到自旋运动旋转频率和半径的估计值分别为40.0 Hz和0.79 m，从而提取得到了自旋微动特征。与旋转频率和半径的真实值相比相差不大，这表明本文所提方法能够有效提取自旋目标的微动特征。

实验2 多散射点模型。若一个目标由两个散射点构成，它们初始位置分别为P1(0.8 m, 8π/15 rad,π/3 rad)T和P2(0.8 m, 7π/15 rad, 5π/6 rad)T，平动和自旋参数以及雷达参数设置如表1所示。如图7所示，图7(a)为观测时间0～1 s内的目标角多普勒频移时频分析结果，而图7(b)和图7(c)分别为图7(a)中两个方框内局部放大的结果。分别从角多普勒频移时频分析结果中获取测量数据。对于P1，取上确界与角多普勒曲线的第4个交点坐标(0.07355 s, 32.25 Hz)和第34个交点坐标(0.8247 s,32.25 Hz)，得到自旋运动旋转频率和半径的估计值分别为39.9 Hz和0.85 m。对于P2，取下确界与角多普勒曲线的第2个交点坐标(0.02347 s, 32.75 Hz)和第36个交点坐标(0.8478 s, 32.75 Hz)，得到自旋运动旋转频率和半径的估计值分别为39.9 Hz和0.86 m。与单散射点模型相比，微动特征提取误差有所增加，这是由于从角多普勒频移时频分析结果中测得的数据误差增大造成的，可以通过增加时频分析方法的分辨率来解决。

图5 角多普勒频移理论值和观测值对比

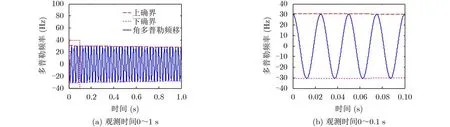
图6 角多普勒频移与其上、下确界关系曲线

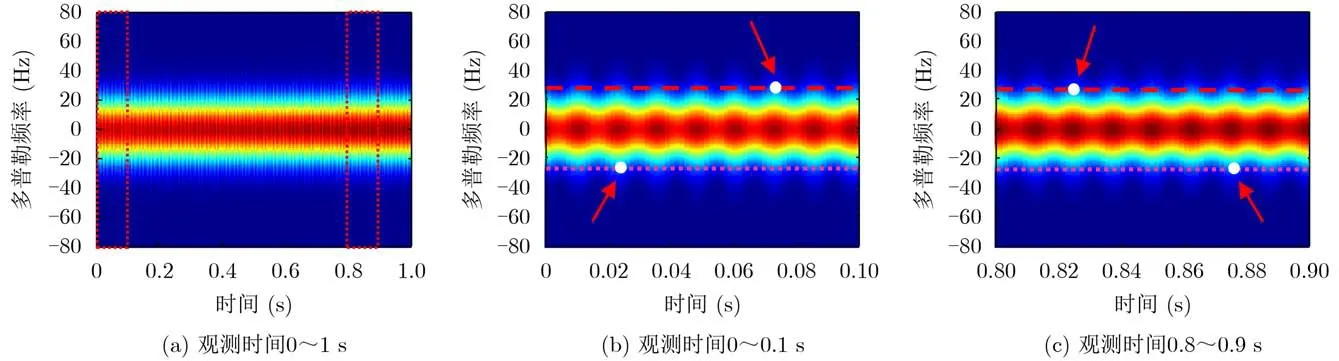
图7 自旋目标角多普勒频移时频分析结果

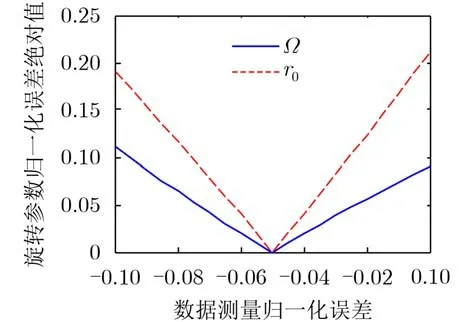
图8 旋转频率和半径的归一化均方误差绝对值的变化曲线

5 结束语

本文研究了利用涡旋电磁波雷达对自旋目标进行探测，通过测量角多普勒频移实现自旋微动特征提取，提出了基于角多普勒频移的自旋微动特征提取方法。本方法与传统平面波雷达测量线多普勒频移提取微动特征方法相比，在目标自旋运动轨迹垂直于雷达视线方向的情况下仍然适用。

本文研究结果表明，基于角多普勒频移表示的多普勒效应和微多普勒效应是十分复杂的，并不像线多普勒频移中可以用二者的线性叠加表示，因此无法进行单独处理。此外，还存在一些问题值得研究，如实际应用中的目标通常有多个散射点构成，需要对不同散射点角多普勒频移的分离方法进行研究；噪声影响尚未考虑，需要对从相位中有效测量角多普勒频移所需信噪比进行评估等。我们将在今后的工作中对其进行进一步研究。