基于列生成的高速铁路车站作业计划调度调整方法研究

张若惠 ，王奇志，田海宁，苗建瑞，谭忆涵

（1.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；2.北京交通大学 交通运输学院，北京 100044；3.中国铁路沈阳局集团有限公司 调度所，辽宁 沈阳 110001)

0 引言

京张高速铁路的开通运营标志着我国正式进入智能高速铁路时代，意味着高速铁路将在运输组织、客运服务、安全监控等方面实现智能化升级[1]。智能调度不仅是实现铁路高效运营管理的有效措施[2]，更是实现高速铁路全网智能运营的基础保障。作为铁路运输的关键节点，大型高速铁路客运站复杂的线路结构和运用规则，导致车站作业调整成为智能调度技术的一个难点。

当高速列车发生晚点，导致既定的车站作业计划不可执行时，需要实时调整列车到发线、进路甚至到发时刻，以恢复列车的正常运行秩序。既有研究[3-6]表明采用高效的调整方法可减少列车晚点对车站作业秩序的影响。为满足车站作业计划调整的高时效性要求，彭其渊等[7]考虑车站设备故障及列车晚点的情况，对高速铁路列车到发时刻及进路调整方法进行了研究。马驷等[8]结合道岔分组方法研究了车站作业计划调整问题。为了便于描述列车冲突，彭其渊等[9]在使用离散时空资源描述到发线的基础上，建立了客运站到发线运用调整的整数规划模型。李涛等[10]运用数理统计方法预估列车到发时刻，并建立了客运站到发线运用优化模型。高速客运站的调整计划既包含到发线和进路的调整，也包含列车到发时刻的调整，既有研究大多侧重某一个方面，将所有调整内容一体优化的研究目前较少。基于以上分析，并结合车站的实际运营情况，构建基于离散时空网络的多商品流的车站作业计划一体化调整模型，根据调度调整实时性需求和模型特点，设计基于列生成的启发式算法，并以长春西站为案例进行验证。

1 车站作业计划调整问题分析

1.1 问题描述

在具有动车组接续关系的终到和始发列车停靠同一到发线，且不考虑车站内进行动车组重联和拆解的条件下，所有列车在高速铁路客运站办理的作业流程都可归纳为进站、占用到发线和出站3 个作业环节。高速铁路车站作业计划调整就是当列车运行发生干扰时，在满足车站作业安全间隔时间、列车技术作业需求、线路和进路运用规则等约束的基础上，快速地为各列车安排合理的到发线、进出站进路和到发时刻，以确保车站的服务水平及作业组织的有序性。

由于列车运行具有时空属性，其在车站内的作业过程可表述为从进站端至出站端的一条时空轨迹。一般而言，列车根据其作业的起止时刻在空间上有多条可选用的线路。若选取道岔、到发线等站内关键设施来刻画车站的空间结构，并将时间按照一定的精度进行离散化时，列车的时空轨迹可用由〈关键设施，离散时刻〉构成，且按时间顺序排列的二元组序列描述。

若将〈关键设施，离散时刻〉二元组实例作为节点，以关键设施之间的空间联系和时间步进关系作为弧，由此可构建一个离散的车站作业时空网络。此时，车站作业计划调整问题就是在该网络中为每列车寻找一条与其他列车无冲突，且满足其作业要求的最优路径的组合优化问题。若将列车看作商品，列车的进、出站看作商品在时空网中流进和流出，车站作业计划调整问题则抽象为基于离散时空网络的多商品流问题。

在此基础之上，由于列车占用设备具有一定时长及列车之间必须保持安全间隔时间的特性，车站作业计划调整需要解决对设备占用和间隔时间刻画的问题。因此，以下针对性分析车站作业离散时空网络的构建、线路占用时间的刻画。

1.2 车站作业离散时空网络构建

为了能够刻画列车的到发方向、列车对线路的排他性占用原则，以及不同种类列车对线路的选择规则，以站界、轨道区段分界点及到发线中心等位置作为关键设施。二元组中的离散时刻是对自TS时刻起至TE时刻止的调整时间段[TS，TE]，以Δ为单位，如1 s 或5 s，进行离散后形成的一系列时刻点。以上的关键设施和离散时刻点则构成离散时空网络中的实体节点集合。实体节点表示列车在何时处于何处。除实体节点外，为了便于搜索列车路径，给每列车设置一个用来表示其开始和结束的虚拟起点和虚拟终点。这类虚拟节点上的关键设施和离散时刻均没有具体的物理含义，其作用仅表示搜索的起点和终点。

网络中的边分为连接实体节点之间的作业弧，以及实体节点和虚拟节点之间，虚拟节点与虚拟节点之间的虚拟弧。作业弧包括用来表示列车从一个位置位移到另外一个位置的运行弧，列车在弧上的运行时间就是2 个节点之间的时间差；还包括用来表示列车在到发线上停留的作业弧。作业弧连接的2 个节点的关键设施属性必须为到发线类，同时离散时刻属性不能相同。虚拟弧包括表示列车进入时空网络的虚拟进站弧和表示列车驶离时空网络前往虚拟终点的虚拟出站弧，即分别为由虚拟起点转移至实体节点和由实体节点转移至虚拟终点所对应的虚拟弧；还包括由虚拟起点至虚拟终点的虚拟弧，该弧表示列车的虚拟路径，若列车选择该条路径，则表示该列车在实际中没有无冲突路径可选择。以下以一个虚构的车站为例对车站作业离散时空网络进行详细说明。

虚构车站作业时空网络示意图如图1 所示。车站空间网络如图1a 所示，其中节点表示车站关键设施，边表示连接关键设施之间的线路。将时间进行离散化处理后，构建的车站离散时空网络如图1b 所示。其中纵轴上的数字代表空间网络中节点的编号，横轴上的数字代表离散时刻的编号。在图1b 中给出了列车停靠3G 的空间路径(虚线)对应的2 条时空路径和一条虚拟路径。该网络中的时空节点包含由实心圆表示的含有〈关键设施，离散时刻〉物理意义的实体节点和由空心圆表示的虚拟节点。网络中的运行弧表示列车在站内的走行过程，如弧B；停站弧表示列车在到发线上的停留过程，如弧C；弧A 和弧D 分别为虚拟进站弧和虚拟出站弧，表示列车在时空网络中的生成与消失。

图1 虚拟车站作业时空网络示意图Fig.1 Diagram of time-space network based on virtual station operation

1.3 线路占用时间刻画

目前，列车在高速铁路车站中的走行均以进路为单位，且进路采用一次锁闭和分段解锁的联锁方式。列车在车站的走行和停留过程可体现为对轨道区段占用和释放的过程。根据时空网络的构建方法，可知每个作业弧对应的是一个轨道区段，因而如何刻画轨道区段的占用就成为精准描述车站作业过程的基础。闭塞时间(Blocking Time)[11]是一种刻画列车排他性占用特定范围线路的描述方法，既可以描述列车在线路上的走行时间，也能描述列车之间的间隔时间。列车占用轨道区段的闭塞时间如图2 所示，主要由以下3 部分构成。①锁闭时间：指自开始办理列车进路时刻起至列车头部到达轨道区段入口处止的时间范围，表示为T锁闭。②运行时间：指列车头部自轨道区段入口处运行至轨道区段出口处的时间范围，表示为T运行。③清空时间：指自列车头部越过轨道区段出口处起至该轨道区段解锁时刻止的时间范围，表示为T释放。

图2 中a12为列车k1，k2先后占用轨道区段q的空闲间隔时间，结合两列车在q上的闭塞时间，其间隔时间为则为列车k1，k2使用轨道区段q的最小安全间隔时间，若a12＜ 0，即k1的闭塞时间与k2的闭塞时间发生重叠，表示k1与k2在使用轨道区段q时有冲突。

图2 列车占用轨道区段的闭塞时间Fig.2 Blocking-time of track sections occupied by train

2 车站作业计划调整模型与算法

2.1 车站作业计划调整模型构建

为便于研究车站作业的调整，做出以下假设：列车折返作业均为同到发线立折；不考虑动车段能力限制；若当前时刻距列车调整到达时刻小于指定时长时，该列车的到发线不能被调整。从减少调度、车站作业工作量及方便乘客出行的角度出发，调整车站作业计划时，应使列车总晚点时间最小，尽量避免列车晚点在路网中的传播；同时，在满足列车作业要求的前提下尽可能少地调整到发线运用方案，以减少对车站作业秩序的影响。以列车晚点时间最短为首要调整目标，以减少车站作业秩序影响为次要调整目标，并通过线性相加将双目标转换为以时间为量纲的单目标，构建车站作业计划调整模型为

式中：Φ 为总目标函数；K为调整时间段内的列车集合；λk为列车权重参数，列车等级越高该值越大；分别为列车k∈K的调整到达时刻和出发时刻；分别为列车k∈K的图定到达时刻和出发时刻；p为时空路径编号；Pk为列车k的备选时空路径集合；e(ijst)为时空弧；i，j为车站关键设施；s，t为离散时刻；E为时空弧集合；是否包含于p中，若包含于则为列车k使用e(ijst)的成本，其中为列车k占用e(ijst)的时长，为列车k占用e(ijst)的单位时间成本；为0-1 决策变量，当列车k选择时空路径p时，= 1，否则，=0；参数ε1，ε2分别为列车早点到达和晚点出发的时间裕量；ωk为列车k的最小停站时间；Ee(ijst)为时空弧e(ijst)的冲突弧集合，对于任意e(ijst)∈E，若存在e(i"j"s"t")∈E与其闭塞时间发生重叠，即e(ijst)与e(i"j"s"t")具有冲突关系，则有e(i"j"s"t")，e(ijst)∈Ee(ijst)成立。

公式(1)表示列车的广义成本之和最小，其中第1 项表示列车加权晚点时间，第2 项表示列车使用时空路径的成本；公式(2)和公式(3)表示调整后的列车到达和出发时刻只能在图定时刻周边一定范围内取值；公式(4)表示列车的停留时间应满足其最短作业时长，通过列车的ωk取值为0；公式(5)表示每列车只能从其备选路径集合Pk中选择一条时空路径约束；公式(6)表示线路的排他性占用及间隔时间约束，即任意2 列车不会选择具有冲突关系的时空路径。

2.2 基于列生成的启发式算法

车站作业计划调整模型是建立在可行列车时空路径集合∪Pk上的，该集合规模较大且存在全部枚举困难的问题，但由于模型的优化解是由各列车的最优或较优路径构成，因而该问题只需在质量较好的时空路径子集中求解即可。列生成算法[12]是以隐枚举的方式提供较优子集的有效算法。其求解思路为：先在不考虑冲突约束的条件下寻找每列车的最优路径，生成路径备选集；若列车最优路径之间存在冲突，则为有冲突的列车寻找次优路径，并加入路径备选集；以此循环迭代，直至生成无冲突的最优解。针对时空路径组合优化问题，列生成算法将其分解为限制性线性松弛主问题(RMP)，用以在较优子集中寻找无冲突的路径组合；以及最短路子问题，用于动态地为列车生成备选路径子集。

2.2.1 模型分解

（1）限制性线性松弛主问题。针对∪Pk过大的问题，为每列车定义其备选路径集合Bk⊆Pk，并使用Bk代替Pk，将车站作业调整问题转换为一个规模较小的问题。由于该问题仍然是求解困难的0-1 整数规划，为此将其整数约束松弛，即0 ≤≤ 1，使其成为易于求解的RMP。RMP 求解后，若得到整数解，则表明已得到车站作业计划调整问题的最优解。若得到含分数的解，则表明存在进路冲突，此时用求解中产生的对偶变量激发子问题，以生成新的可行路径，实现对Bk的扩容。反复迭代，直到找到最优解或无法产生新的可行路径为止。

（2）最短路径子问题模型。子问题的目的是为列车寻找新的较优可行路径。公式（2）—公式（4）对车站作业离散时空网络中的弧进行限定后，根据列生成的思想，最短路径子问题模型表示为

式中：σk为子问题的目标函数；为0-1 变量，当列车k选择e(ijst)时，分别为公式(5)和公式(6)的对偶变量。

最短路径子问题模型利用公式(7)来判断列车k是否有更优的时空路径：若σk＜0，则说明为列车k搜索到一条费用更小，能使目标函数下降的时空路径，并将其加入到Bk中。

2.2.2 启发式算法

RMP 是原问题的线性松弛问题，当最优解是非整数且子问题无法生成新路径时，需要将RMP的解转换为原问题的可行解。利用RMP 对偶问题的最优解为启发信息，定义列车的重要度为

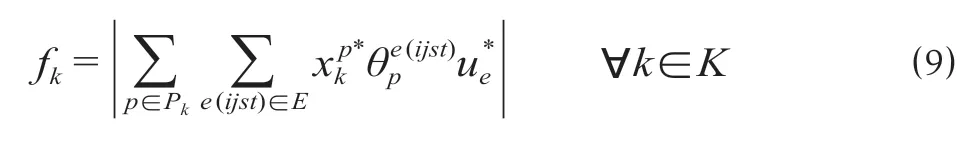
式中：fk为列车的重要度，该值越大表示列车越重要；为RMP 的最优解。

启发式算法为：首先对fk的值由大到小进行排序，之后采用最短路算法按顺序为每列车寻找时空路径。若出现无解列车，则调整列车顺序，每次优先铺化前次无解列车，以此迭代，直至找到可行解。

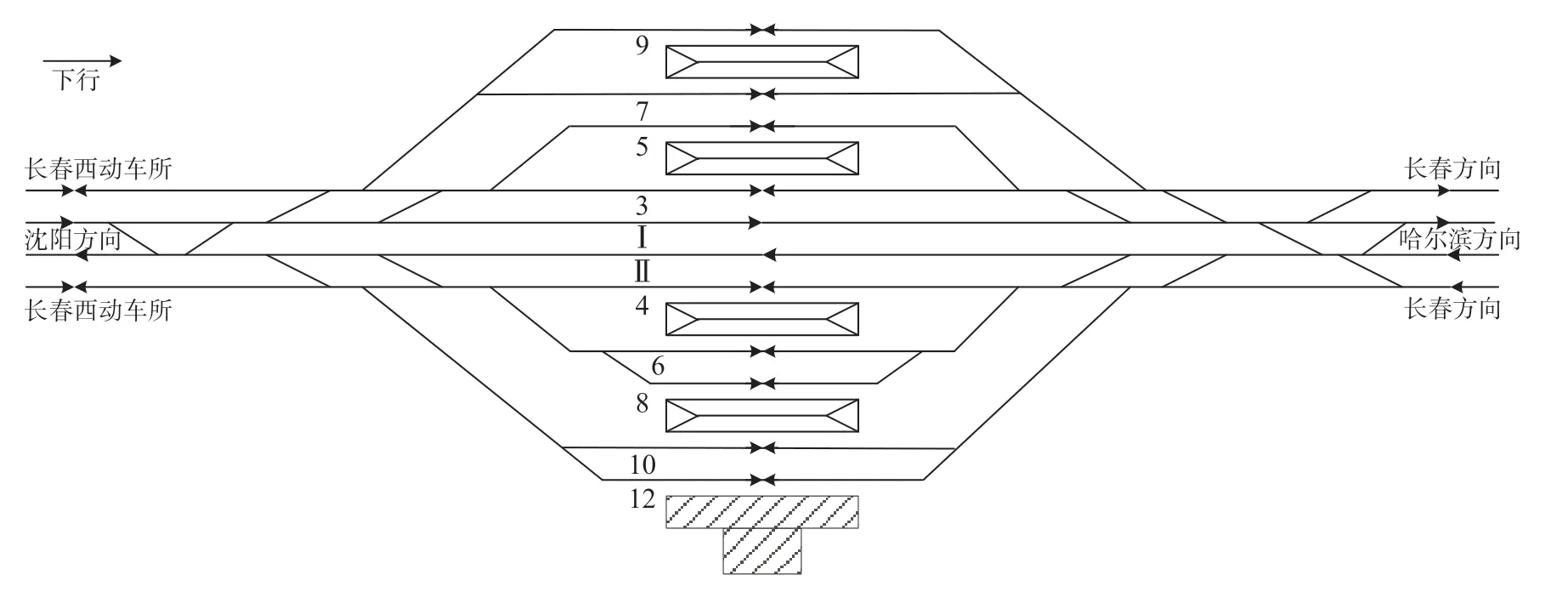
图3 长春西客运站站型图Fig.3 Layout of Changchun West Railway Station

3 实例验证

以长春西高速铁路客运站为例对模型和算法进行验证。车站衔接沈阳、哈尔滨、长春3 个方向，以及长春西动车所，长春西客运站站型图如图3 所示。Ⅰ，Ⅱ正线只接发下、上行通过列车；其余9条到发线可用于接发上、下行列车，其中3，4 道可供长春站始发终到动车组出入段走行使用。列车占用到发线的费用如表1 所示，“-”表示该列车不能使用对应的到发线。车站咽喉区采用分段解锁，各轨道区段的占用时间根据其位置、列车长度、运行速度等因素确定。在考虑变通进路条件下共有192条接发车进路。

令当前时刻为15 : 00，按照提前2 h 下发计划到车站的规定，设置调整阶段为17 : 00—19 : 00，调整范围内的列车共计29 列。其中OD4606，OG4723为出段去往长春始发的动车组，在本站无作业；C1016 为长春站终到，通过本站入段的动车组；G8017 为通过列车，其余为停站列车。17 : 00—19 : 00 时段图定车站作业计划如图4 所示。

列车权重λk设置通过列车为100，停站列车中G = 30，C = 20，D = 10。离 散 时 间 间隔∆取值15 s。最小停站时间设置为120 s。在此基础上，假设G4116 预计晚点5 min，G716 晚点13 min，G755 晚点6 min，G4722晚点10 min到达。

依据车站作业计划调整模型和基于列生成的启发式算法，在CPU 为Intel (R) i7-8550U 3.0GHz、内存为8G 的电脑上，运用C#编程，并调用CPLEX12.6.2求解RMP 模型。列生成计算得到的结果是整数解，目标函数值为138 490 s，得到的是原问题的最优解，列生成算法收敛过程如图5 所示。经验证，启发式算法得到的可行解和列生成算法得到的结果一致，程序共运行23 s，说明基于列生成的启发式算法可在短时间内得到质量较高的满意解。

车站作业计划调整方案如图6 所示，图中红色线条标记的是到发线或到发时刻发生调整的列车，黑色线条标记的是没有发生任何调整的列车。

表1 列车占用到发线的费用Tab.1 Occupancy cost of arrival-departure tracks

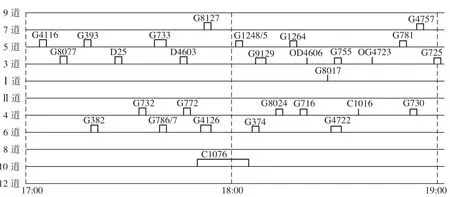
图4 17 : 00—19 : 00 时段图定车站作业计划Fig.4 The planned station operation plan during 17 : 00-19 : 00

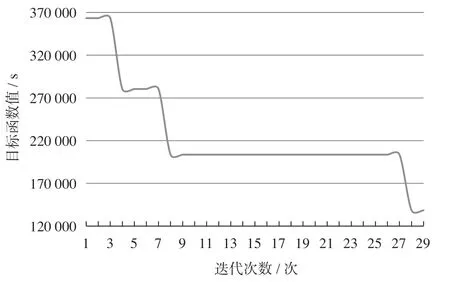
图5 列生成算法收敛过程Fig.5 Convergence procedure of the column generation algorithm

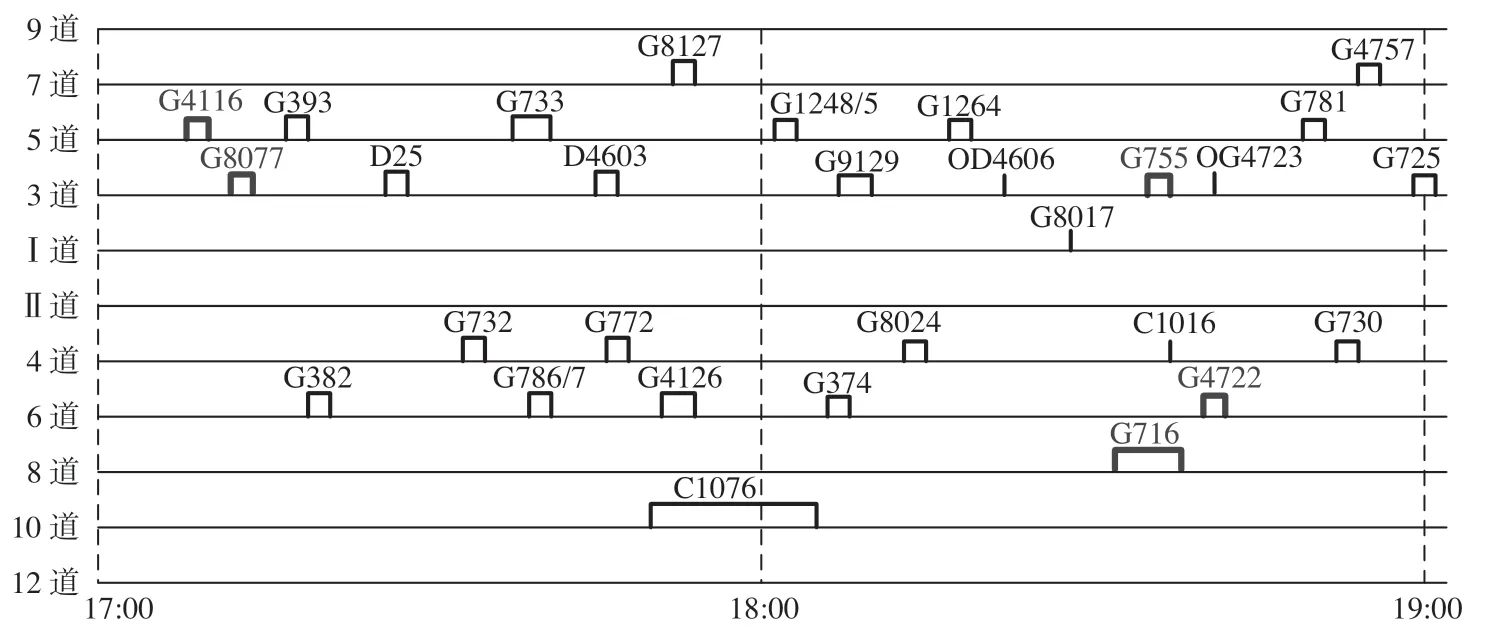
图6 车站作业计划调整方案Fig.6 The rescheduling solution of station operation plan

将图4 和图6 对比分析得：①G8077 受G4116延误的影响产生延误60 s；②G716，G4722 晚点后的列车进路与C1016 的通过进路分别发生冲突，为保证C1016 正点通过并减少总晚点量，将G716由4 道调整为8 道，等待C1016 通过之后再发车，G4722 增晚60 s 到达且停站时间由180 s 变为120 s。其余列车的到发时刻及到发线运用方案保持不变。经调整后，在满足车站线路能力等约束的基础上，列车总晚点时间增晚120 s，以减少列车晚点对车站作业秩序的影响。干扰条件下列车信息调整结果如表2 所示。

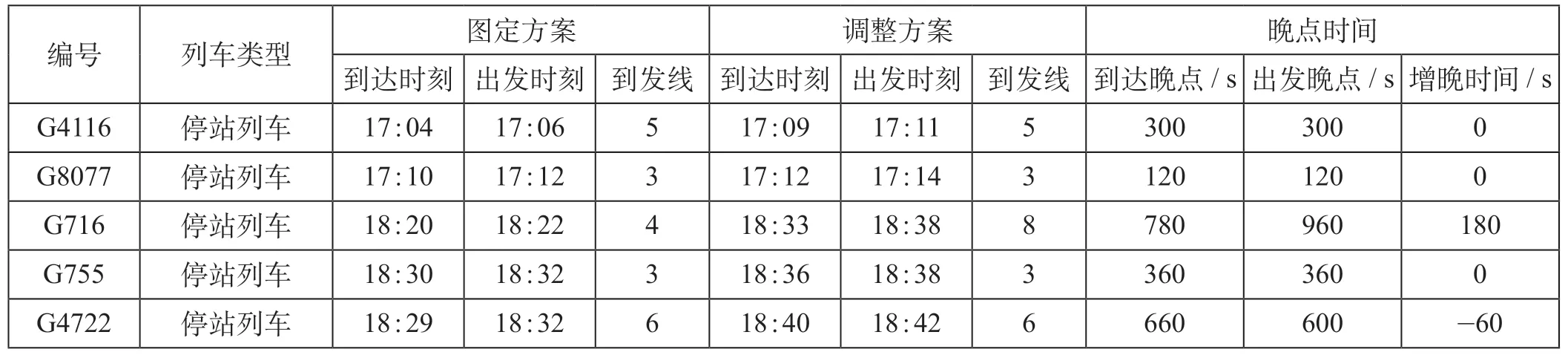
表2 干扰条件下列车信息调整结果Tab.2 Adjustment results of train information under interference condition

4 结束语

大型高速铁路客运站作业计划实时调整是行车调度调整的关键内容，也是技术难点所在。针对调度调整高时效性、高精度的要求及车站作业的实际约束条件，运用数学优化方法构建相应的模型和快速求解算法，能实现列车到发时刻、咽喉进路和到发线的实时同步调整。通过实例验证表明，该模型可以有效解决大型高速铁路客运站作业计划调整问题，并且能够同时兼顾车站运营的高效性和乘客出行的便捷性，快速生成的调整方案可作为列车调度员调整的参考依据。然而，还需要进一步考虑调车与行车作业之间的交叉干扰，以实现车站作业计划的综合实时优化调整。