指向数学素养 理解概念本质——《分数再认识》教学例谈

□周蓉蓉 邓双英

【课前思考】

目前，国内各版本教材都将分数安排在两个阶段进行教学。第一阶段一般安排在三年级，主要内容为借助直观模型，引导学生通过直观操作，经历分数的产生过程，并从部分与整体的关系初步理解分数的意义。第二阶段一般安排在五年级，将学生对分数的感性认识上升到理性认识，概括出分数的意义，从分数与除法的关系等方面加深对分数意义的理解。五年级下册《分数的意义》一课的主要教学内容是通过实例概括出分数表示整体与部分之间关系的意义，进一步理解分数表示多少的相对性。

从三年级的分数初步认识到本节课的分数再认识，学生对分数意义的理解掌握情况是怎么样的？知识的衔接点和困难点在哪里？为了更好地了解学情，课前笔者对本校五年级225名学生进行了问卷调查，前测题及结果如下。

用分数表示下面各图中的阴影部分题1images/BZ_51_460_1109_678_1149.pngimages/BZ_51_769_1094_884_1164.png①号图形②号图形③号图形结果统计26：90.5%2 6：71.4%2 6：42.9%13：2.4%画图表示13：9.5%1 3：38.1%题2 3 4 的意思1个图形的4个图形的8个图形的结果统计错误率：9.5%34：61.9%3 4：26.2%3 4：2.4%

根据前测分析，以下问题值得思考：①如何帮助学生完善对于“一份的概念”的理解？②如何改编教材，呈现学习材料，帮助学生突破对“整体”认识的局限性？③除了从“平均分成几份，取若干份”份数定义角度认识分数，这节课还需要“再认识”什么？

结合课前思考，笔者从以下几个方面展开教学。

【教学实践】

（一）数形结合，唤醒经验，再认识“的特征”

图1

（二）理性思辨，深化内涵，再认识“一个整体”

2.拓展外延，理解深化“一个整体”

针对前测中部分学生认为“一个整体中的物体或图形必须是完整的、同类型的、明确数量的”这一状况，以及学生在后续学习中会经常面对各种各样的数量作为“一个整体”的现实，笔者增加了关于“一个整体”的学习环节，依托三个典型例子，拓展“整体”概念的外延，深刻理解其内涵。

（1）3名学生和1名老师

师：“3名学生和1名老师”能作为一个整体吗？

生：可以。

生（齐）：能。虽然它只是半块巧克力，但依然可以作为一个整体。

（3）6米（7米，……，x米）

师：我们用一条线段来表示6 米，它可以作为一个整体吗？

生：可以把x 平均分成4 份,取出其中的3 份就行了。

师：这个不确定的数量依然可以作为一个整体。如果把x米换成m千克，还可以吗？（生答）

师：再换。（出示0.8米的绳子、买5本书的总钱数、学校占地面积）

生（齐）：都是可以的。

板书：

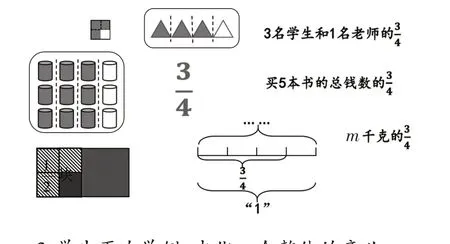
3.学生再次举例，内化一个整体的意义

这里的学习材料形式多样，有用图表示的，也有用语言表述的；有具体的，也有不确定的；有教师提供的材料，也有学生举的例子，充分体现了“一个整体”的丰富性与全面性。这个学习过程，从图到文字，从数到字母，从一个到多个的集合，从具体到抽象，学生经历了“一个整体”概念形成、发展、拓展的过程，有效地改变了原有的认知经验，再次认识到“一个整体”外延的丰富性、内涵的深刻性。

（三）从点到面、抽象概括，再认识“分数意义”

师：同学们，学到这儿，你能用自己的话来说说什么是分数吗？

生：把一个整体平均分成几份，取其中的几份，就是这个数的几分之几。

生：把一个整体平均分成n 份，取其中的x 份，就是分数的几分之几。

师：同学们，虽然他们的说法不同，但都抓到了分数的基本特征。数学家也是这么说的，一起来读一读。

生（读）：把一个整体平均分成若干份，其中的一份或几份，可以用分数表示。

师：这里有一个词语，若干份，你觉得是什么意思？

生：x份。

生：多少份都可以。

师：是的，不管多少份都可以，这就是分数的意义。

（四）充分体验，借助推理，再认识“分数相对性”

分数的相对性包括：整体不同，相同分数所对应的具体数量不同；整体相同，不同分数所对应的具体数量不同；整体不同，不同分数所表示的数量却可能相同。这与整数表示数的多少有很大的区别，需要教师在教学中引导学生经历、体会、感受、领悟、总结，让学生学会有根有据地进行表达，充分认识分数的相对性，培养推理能力。

活动一：做一做

②猜：信封里放的笔的总数。

③讨论：大家的猜想对吗？理由是什么？