如何借助辅助线理解图形放大与缩小问题
2021-04-06邓招徒
□邓招徒
“图形的放大与缩小”是学生理解相似图形的基础。三角形和多边形的放大和缩小,常常让学生感到困难。在教学实践中,教师可以利用辅助线帮助学生更好地理解这个难点。
一、探寻三角形的放大与缩小
(一)呈现问题
在图1 上画出将三角形ABC按1∶2缩小后的图形。

图1
(二)引导交流


图2
学生可能找到AB和AC的中点D 和E,连接DE 后得到的三角形ADE 就是三角形ABC 按1∶2 缩 小 后 的 图形。(如图2)

学生可能会从对应高的比这一角度进行说明,也可能会从中位线的角度进行说明。
继续引导:如果按照这样的思路,只能有这一种画法吗?还可以怎么画?
学生可以通过找另外两组相邻边的中点解决问题(如图3)。

图3
3.缩小后的图形面积和原面积有什么关系?得到的三个三角形位置不一样,都符合要求吗?
引导学生发现,缩小后的图形与原图形面积的比都是1∶4。通过平移,将缩小后的三角形重叠,可以看到三个三角形的形状和大小其实都是一样的。
4.还有其他的方法吗?
呈现第4 种方法(如图4):找到三条边的中点连接起来得到三角形DEF,三角形DEF 也是将三角形ABC按1∶2缩小后的图形。
讨论:这样画可以吗?引导学生发现三角形DEF和其他三个三角形的相等关系。
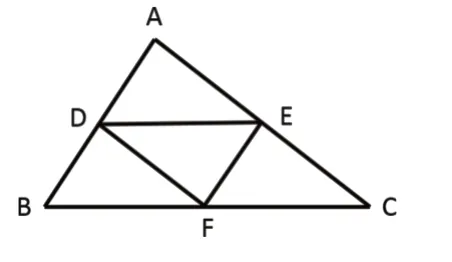
图4
(三)延伸拓展
根据刚才研究三角形缩小的过程,想一想:如果将三角形ABC按照2∶1放大,可能有几种不同的方法?
二、研究多边形的放大与缩小
(一)呈现问题
画出将五边形ABCDE 按2∶1 放大和按1∶2 缩小后的图形。
(二)引导交流
有了刚才的经验,学生比较容易发现将五边形放大最方便的方法是在以点C为顶点引出的四条射线上(如图5)找到CB、CA、CE 和CD2 倍长度的点和中点,顺次连接得到要求的图形。

图5
三、拓展延伸
(一)呈现问题
在原图(如图6)中分别画出将五边形按2:1放大和按1:2缩小后的图形。

图6
(二)引导交流
在学生尝试独立解决问题后,教师组织学生重点交流画辅助线的方法:从五边形的某一个顶点出发,连接不相邻的两个顶点,作两条辅助线,然后再找出中点(缩小)或延长1 倍(放大)画出图形(如图7)。
图7
通过这样的操作过程,学生明确了画放大与缩小图时,找对应边其实就是找到对应点,经历从立到破,又从破到立的过程。学生利用辅助线画出较为抽象的图形的同时,在知识迁移、多角度思考问题和空间想象能力等方面都得到了锻炼。
