基于空间桥面不平顺的简支梁桥冲击系数研究

薛宇欣, 周勇军,2, 赵 煜,2, 王刚强

(1.长安大学 公路学院,陕西 西安 710064; 2.长安大学 公路大型结构安全教育部工程研究中心,陕西 西安 710064; 3.中钢集团 郑州金属制品研究院有限公司,河南 郑州 450001)

汽车以一定速度在桥梁上行驶时,桥梁产生的应力与变形效应比大小相等的静载引起的效应要大一些,这种由于荷载的动力作用使桥梁发生振动而造成内力或变形增大的现象称为冲击作用[1],车辆通过桥梁时对桥梁结构产生的这种竖向动力响应的增大效应用冲击系数μ表示[2]。桥面的凹凸使得实际桥面偏离绝对设计平面,从而导致线形不平整。不平整的桥面会对行驶中的车辆产生新的外界激励,使得桥梁结构的动力响应受到相应的影响,从而导致结构内力与位移发生变化[3]。因此,桥面不平整度是影响桥梁冲击系数的一个关键因素[4]。

在桥面不平整度的模拟研究方面,有研究者采用正弦(余弦)函数曲线模拟桥面不平整度[5-6];文献[7]运用文献[8]中的桥面等级功率谱密度函数建立自回归(autoregressive,AR)模型,并分析了其模拟精度;文献[9-10]分别采用随机相位谐波法、蒙特卡洛法模拟更加符合实际情况的桥面;文献[11]提出采用谐波叠加法模拟桥面不平整度,该方法可以满足车-桥耦合振动的随机性。在桥面不平整度对桥梁冲击系数影响方面,相关研究表明桥面不平整度是影响车-桥耦合系统振动响应的主要激励之一[5,12-13],并且冲击系数随桥面不平整度变差而大幅度增大[14-15]。

传统数值模拟桥面不平整度方法中,通常仅对一条纵向桥面不平整度样本进行模拟,将桥面视为沿纵向一维变化,然后将所得样本分别对车辆左、右轮进行一致输入,计算系统的响应。文献[16]采用非一致输入模拟桥面不平整度,分析车-桥耦合系统振动,但是左、右轮粗糙度相互独立,没有将左、右轮相关性考虑在内;文献[17]采用随机关联法模拟桥梁的横向桥面不平整度,发现横向不平整度关联性越好,不平整度引起的冲击系数越大,忽略桥面不平整度横向差异(完全关联)时所得到的冲击系数偏于保守,但是在工程实践可以接受范围内;文献[18]考虑左、右轮粗糙度相关性后对重型卡车作用下多梁桥动力特性进行了研究,结果表明重型卡车引起的桥梁冲击系数小于美国AASHTO规范[19]计算值;文献[20]考虑桥面不平整度的空间性进行桥面不平整度非一致激励下车-桥耦合振动响应研究,针对采用左右轮、同时采用左轮、同时采用右轮进行输入的3种情形,分别研究实测桥面不平整度对车-桥系统振动响应的影响,结果表明,左右轮对应桥面不平整度相关性较好时,非一致激励输入计算得到的车-桥耦合振动响应基本位于后2种计算响应之间;文献[21]采用近似相似理论模拟相干函数,得到车辆左、右轮之间的频响函数,并将单轮模型拓展为左、右轮迹路面激励时域模型,但是该模型相干函数的通用性较差。上述文献在分析桥面不平整度对车-桥耦合振动响应时，均采用单个桥面不平整度激励样本相干模型,该模型不便于研究车-桥耦合随机振动的统计效应。文献[22]基于通用相干模型,根据文献[23]给出桥面不平整度功率谱密度函数,采用虚拟激励法构建空间桥面不平整度相干模型,研究其对车-桥耦合振动响应的影响,但是未分析车辆随机行驶对桥梁冲击系数的影响。

实际桥面不平整度具有极大的随机性,同时,车辆在桥上行驶过程中轨迹不固定,比如发生变道、超车等情况都会使得车辆行驶轨迹在桥面上发生横向位置的变化,车辆受到来自桥面的激励也具有极大的随机性,以往的数值方法很难准确反映真实桥面不平整度对桥梁冲击系数的影响。本文利用加速度采集客户端进行车辆随机行驶轨迹下桥面不平整度测试,基于空间桥面不平整度进行了车-桥耦合系统响应分析,并和单线程桥面不平整度的结构响应及设计规范值进行对比,以期为桥梁冲击系数研究和结构动态性能评估提供参考。

1 空间桥面不平整度构建

1.1 桥面不平整度模拟

桥面不平整度是引起车辆振动的主要振源之一,大量的试验测量表明, 桥面不平整度是具有零均值、各态历经的平稳Gauss 随机过程[2],准确模拟桥面不平整度是研究车-桥耦合系统振动响应的关键。通常采用功率谱密度函数来描述桥面不平整度等级。目前已有多种形式的功率谱密度表达式模型,常用的方法主要有三角级数叠加法、傅里叶逆变换法等[13]。三角级数叠加法适用于实测桥梁谱的时域模拟,该算法数学推导严密,适用范围较为广泛。傅里叶逆变换法的功率谱密度与原始功率谱密度基本一致,并且该方法便于操作、结果准确。利用傅里叶逆变换法计算桥面不平整度的公式[24]为:

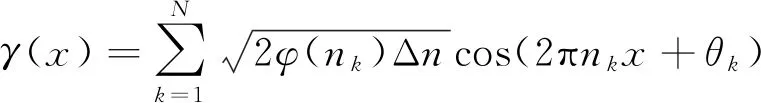
(1)

其中:γ(x)为桥面不平整度;k取值为自然数;φ(nk)为桥面不平整度功率谱函数;nk为波的个数;Δn为空间频率采样间距;x为桥面纵向坐标值;θk为在[0,2π]上均匀分布的随机相位角。

文献[23]中的功率谱密度函数表达式为:

(2)

其中:n为空间频率;n0为(1/2)π的间断频率;φ(n0)为桥面不平整系数,与桥面状况有关;n1、n2分别为截止频率的上、下限。

1.2 桥面不平整度获取

目前,桥面不平整度测量方法主要有纵断面测量、动态响应测量及主观评测3种测试方法。纵断面测量方法由传统的3 m直尺法发展到非接触式动态纵断面测量仪,通过安装在车辆上的发射器向测量面发射微波、声音、红外线、光等介质,测量出反射时间差,继而计算测量面竖向位移;动态响应方法测试精度受测试车辆行驶速度及响应信号干扰等因素影响;主观评测方法是基于人-车-桥系统振动主观感受的测量方法,具有很大的随机性,进而导致检测结果的不确定性。本文采用智能手机测试方法获取桥面不平整度[25],具体方法如下:① 基于复模态理论对1/4车辆模型振动响应方程进行推导,得出质量、弹簧刚度系数、阻尼系数等5个参数与各阶振型系数、固有频率、阻尼比等6个模态参数之间的关系以及加速度响应频响函数;② 通过车辆前轮跌落试验,利用具有加速度采集客户端的智能手机收集车辆仪表板位置的自由衰减振动响应信号;③ 将时域中的振动响应信号进行离散傅里叶变换,进而得到信号在频域中的数据,利用所得加速度响应频响函数,采用基于最小二乘迭代的频域识别方法求解车辆模态参数,并采用遗传算法求解车辆模型的物理参数;④ 由智能手机采集到的竖向加速度数据反算出桥面不平整度。

1.3 桥面不平整度构建

试验桥梁为西安市忠勤路3号公路简支T梁桥,该桥跨径20 m,桥面净宽11 m,主梁混凝土强度等级为C50,桥面铺装层由上至下为10 cm厚度沥青混凝土、0.2 cm厚防水层及10 cm厚C50混凝土现浇层,桥梁横断面尺寸如图1所示(单位为cm)。

建立有限元模型提取桥梁的刚度矩阵、质量矩阵,为Matlab编程提供依据。桥梁上部结构采用ANSYS梁格法建模,根据实际参数建立横隔板以连接横向主梁单元,支座处约束水平和横向位移,ANSYS模型如图2所示。

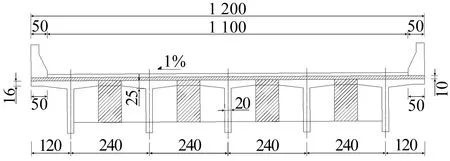
图1 混凝土简支T梁桥横断面

图2 混凝土简支T梁桥有限元模型

实桥试验获得车辆行驶轨迹随机情况下桥面不平整度,实桥试验情形如图3所示。通过对智能手机获得的车辆加速度数值进行处理,可得空间桥面不平整度,如图4所示,具体处理方法如下:① 对桥面进行网格化处理,其中每个节点处桥面不平整度数值均为试验获得;② 通过Matlab对车辆行驶的随机性进行模拟;③ 依据自编Matlab程序,计算车-桥耦合系统振动响应。考虑到桥梁跨径仅有20 m、行车速度较快,以及为了保证行车安全,司机无法在桥跨范围内左右偏移过大距离,规定横向以行车道中心线为基准线,车辆在通过桥梁的时间内,左、右最大偏移量均为0.8 m。桥梁纵向步长0.02 m,步数为1 000;横向步长0.2 m,步数为8。编程计算时桥面网格化示意如图5所示。

图3 实桥试验情形

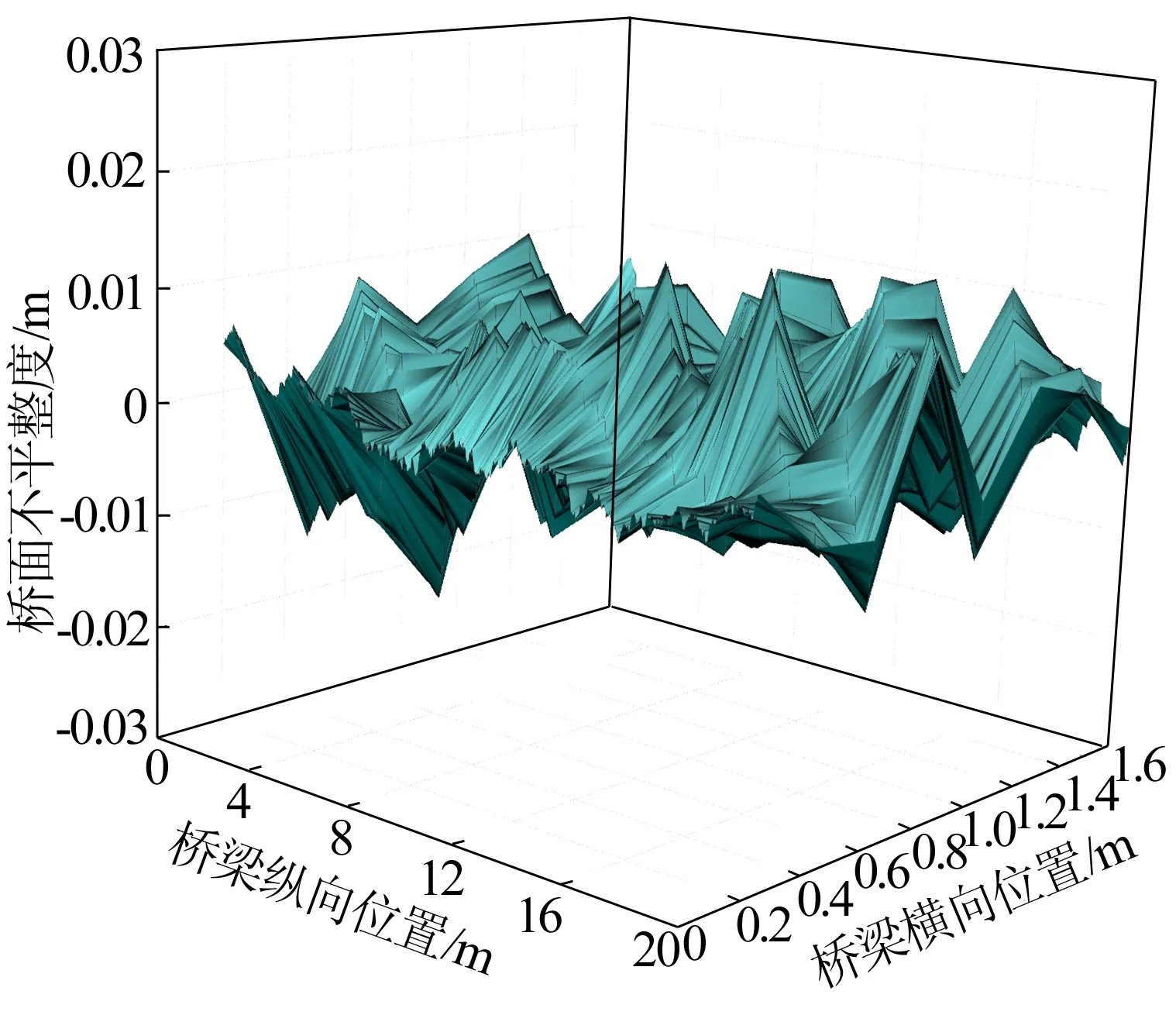
图4 智能手机实测空间桥面不平整度

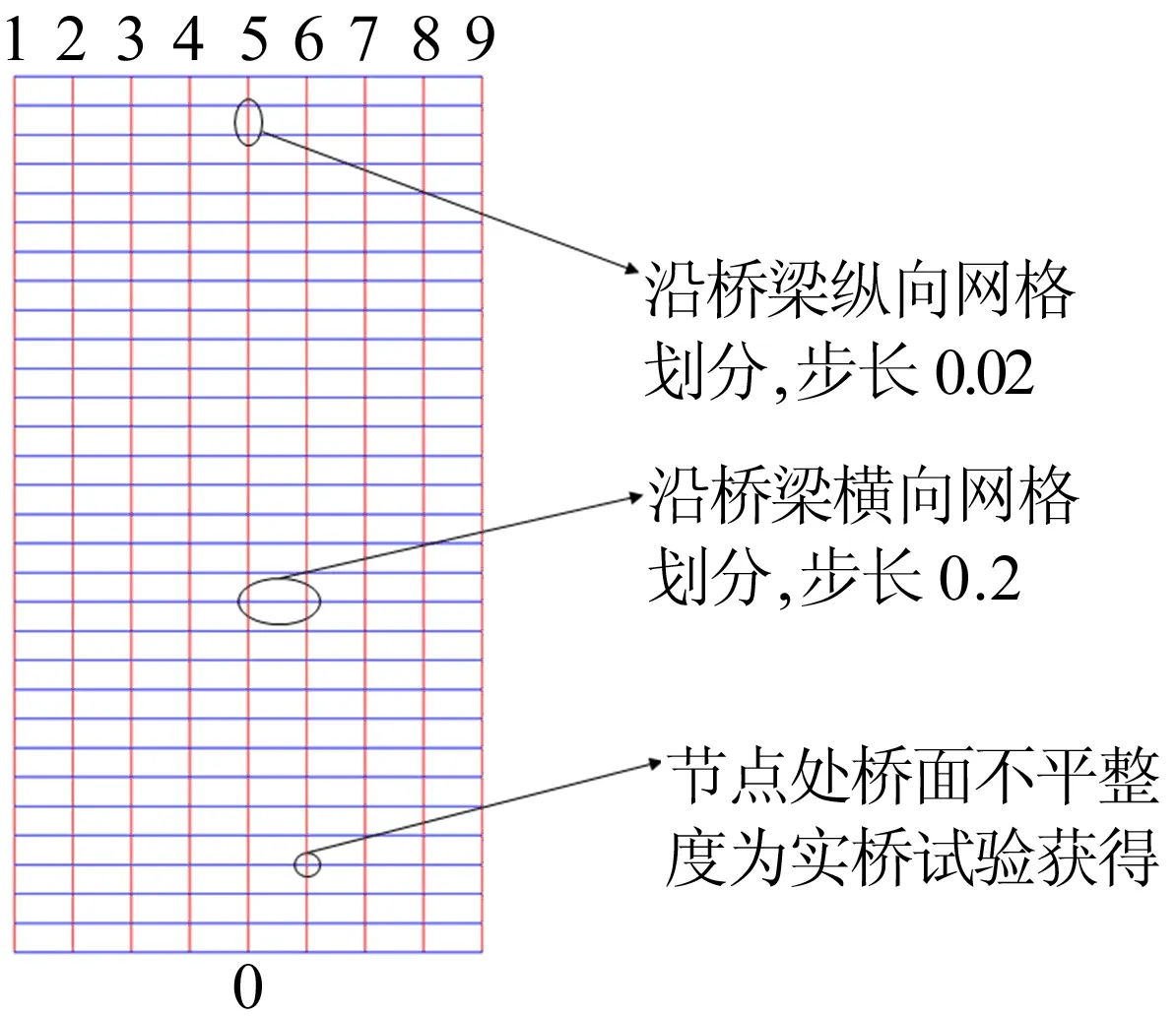
图5 程序中桥面网格化示意图

在车辆行驶轨迹随机的前提下,假定车辆从0点驶入,车辆行驶左右偏移具有随机性,最终从1～9出口随机驶离桥面。采用1/4车辆模型对车-桥耦合振动响应分析时,自由度少、计算量较小,而且车辆模型是否精确对桥梁冲击系数的影响不大,因此本文采用1/4车辆模型,如图6所示。1/4车辆模型参数[26]见表1所列。

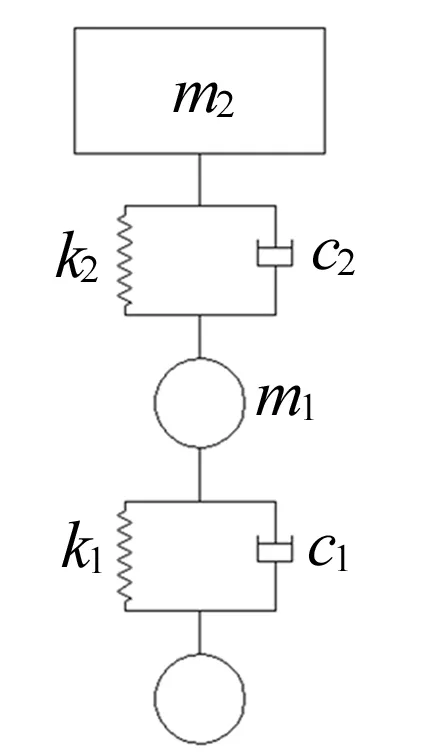
图6 1/4车辆模型

表1 1/4车辆模型参数

2 基于桥面不平整度的冲击系数研究

2.1 基于不同规范的冲击系数计算

《公路桥涵设计通用规范》[27](为了方便对比分析,以下简称“中国规范”)规定冲击系数由结构基频确定，美国AASHTO规范(2017)[28]考虑了极限状态与结构类型，加拿大规范[29]以车轴数与结构类型进行划分，日本规范[30]依据桥梁跨径与结构类型进行计算。由此可知,4国规范计算冲击系数均未考虑桥面不平整度。

利用Lanczos方法计算该桥基频为5.32 Hz,进而可得该桥的冲击系数规范值,4国规范计算冲击系数结果对比见表2所列。

表2 4国规范冲击系数计算值

由表2可知:按照加拿大规范的计算值最大,为0.400,较为保守;按照美国规范为0.330;上述结果均大于按照中国规范计算值0.280;按照日本规范得到的冲击系数最小,为0.175。

2.2 实测单线程桥面不平整度冲击系数计算

在理论分析及研究中,通常采用汽车通过桥梁时对桥梁结构产生的竖向动力效应增大系数表征冲击系数,可以表示为:

μ=(Ydmax/Yjmax)-1

(3)

其中:Yjmax为在车辆过桥时测得的效应时间历程曲线上,最大静力效应处量取的最大静力效应值;Ydmax为在效应时间历程曲线上最大静力效应处量取的最大动效应值。

依据文献[8],采用三角级数叠加法模拟A、B、C 3种桥面状况等级下单线程桥面不平整度,结果如图7所示。

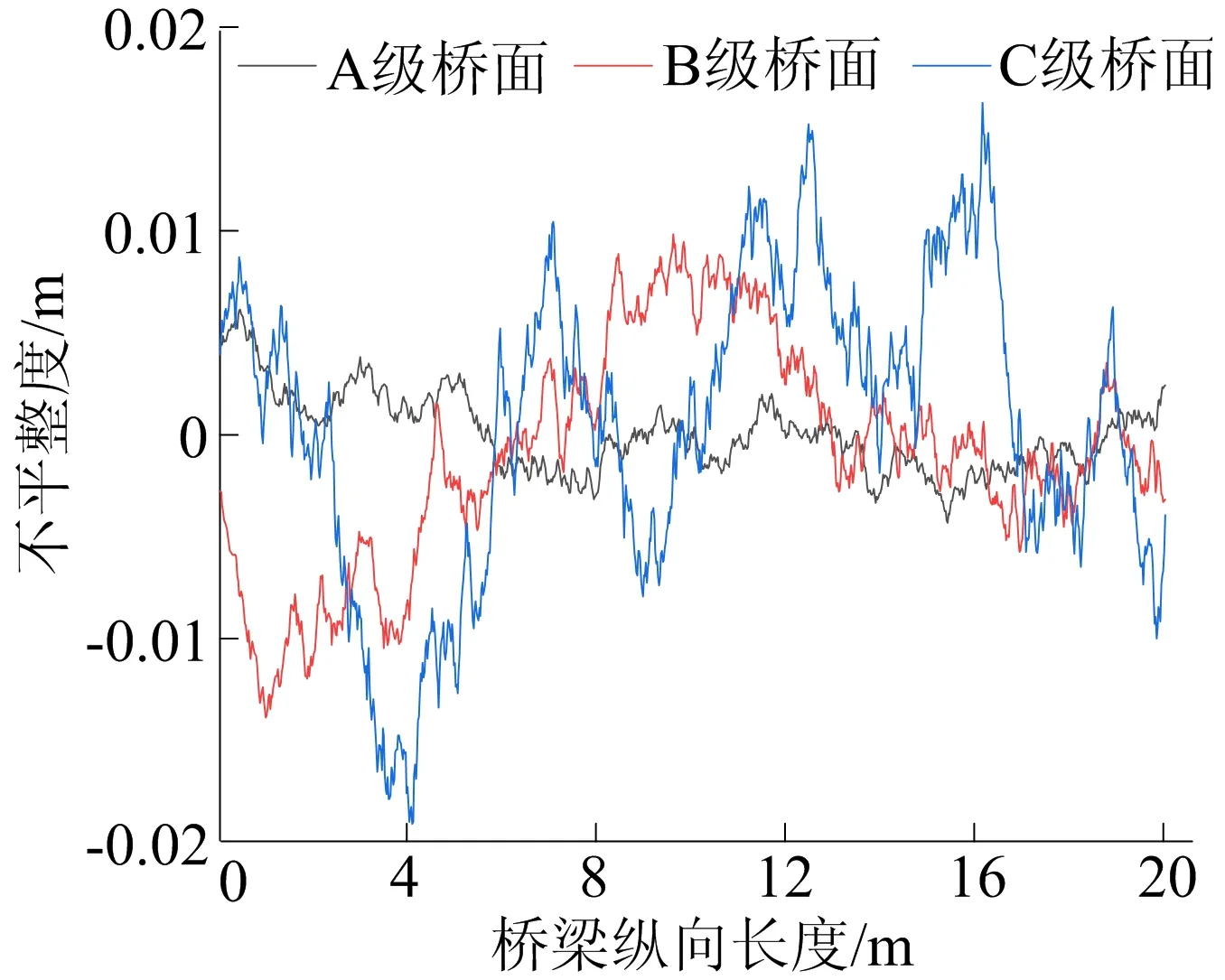
图7 桥面不平整度模拟结果

假定车辆行驶过程中,车辆在桥上横向位置固定(单线程),通过改变车辆行驶速度来研究不同车速(v)条件下桥梁中梁跨中位置振动响应,10、20、30、40 m/s车速下跨中位置位移时程曲线如图8所示。

利用(3)式计算车辆行驶单线程时,不同车速下中梁跨中冲击系数,其变化趋势如图9所示。

由图8、图9可知,随着v增加,桥梁跨中位移响应与冲击系数呈递增趋势;但是当v足够大时(v>30 m/s),冲击系数趋于平稳甚至出现减小趋势。

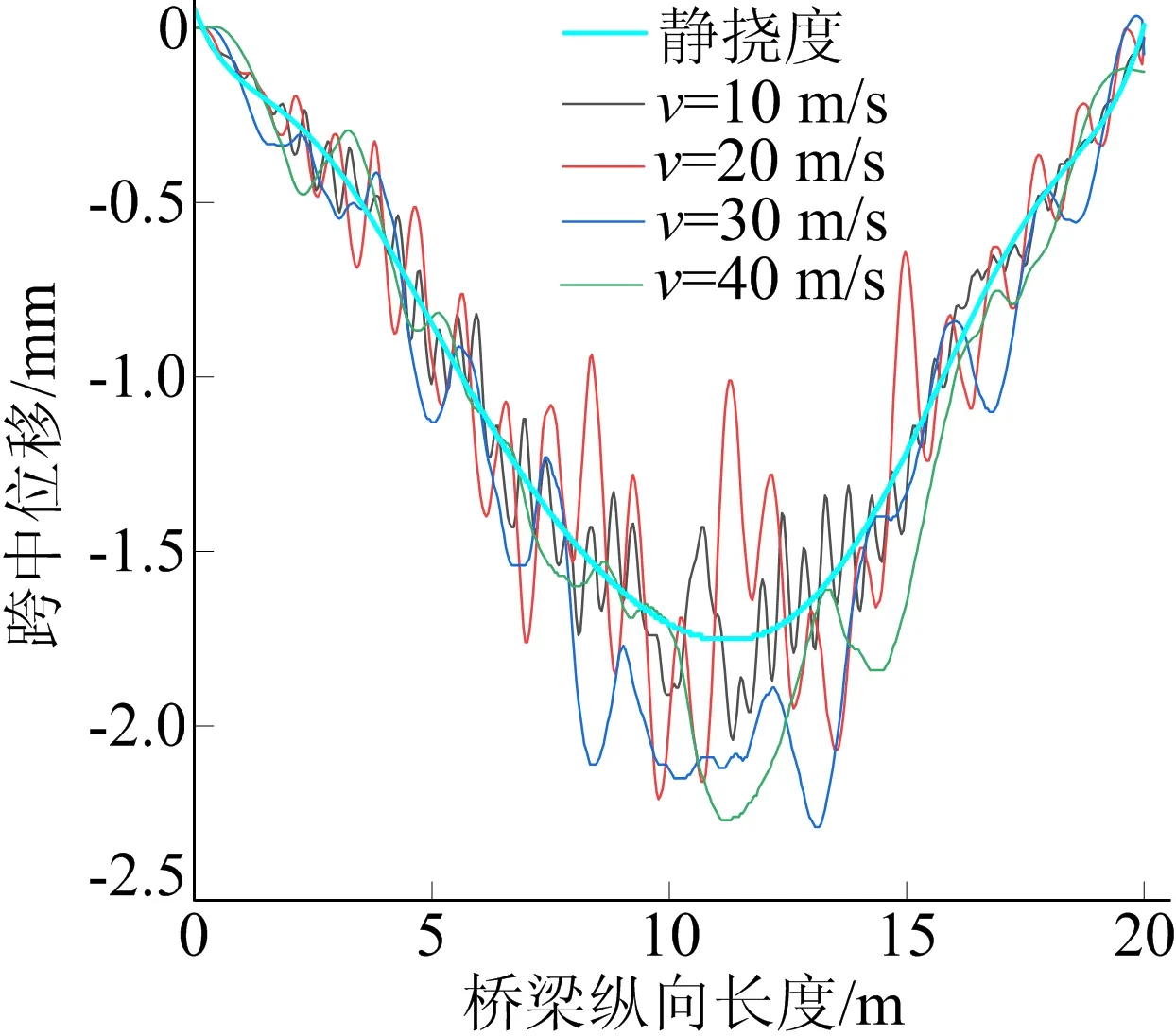
图8 不同车速桥梁跨中位移响应曲线

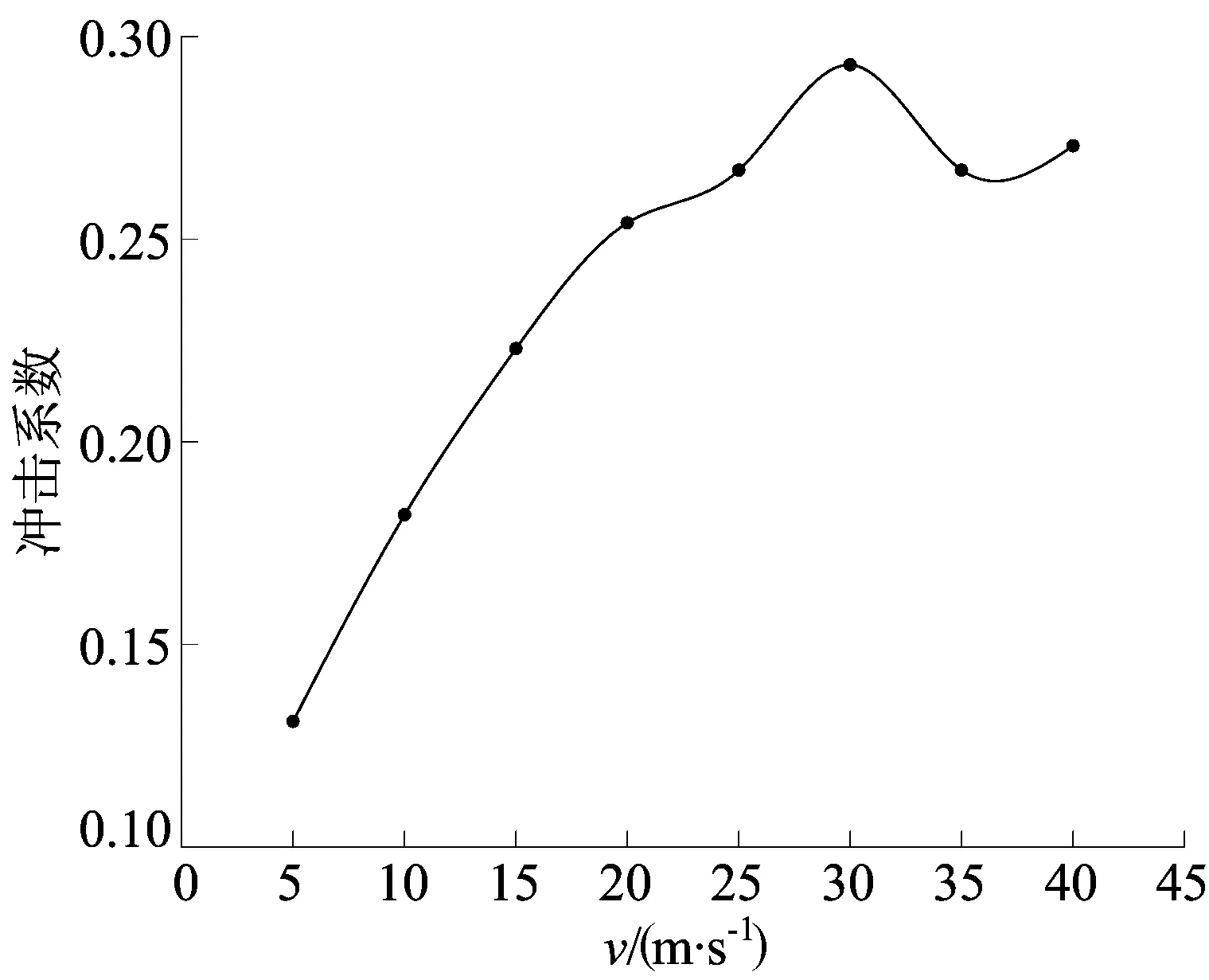
图9 冲击系数随车速变化关系

2.3 实测空间桥面不平整度冲击系数计算

基于伽尔顿板实验原理模拟车辆行驶过程中行驶轨迹的随机性。以中梁为研究对象,20 m/s车速时,车辆随机行驶轨迹下产生500组冲击系数,数据直方图如图10所示。

车速由5 m/s增加到40 m/s产生的500组随机行驶轨迹下冲击系数数据统计特征值变化趋势如图11所示。对同一车速、不同车辆行驶轨迹下产生的500组冲击系数直方图进行K-S检验分析可知,同一车速不同行驶轨迹下冲击系数的概率分布服从正态分布。

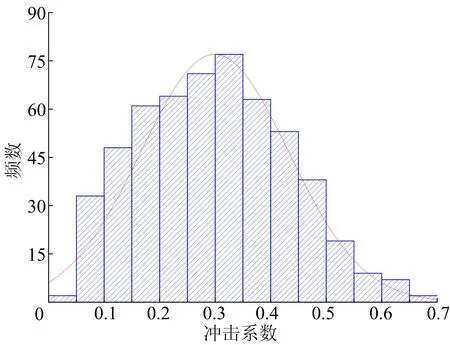
图10 20 m/s时冲击系数直方图

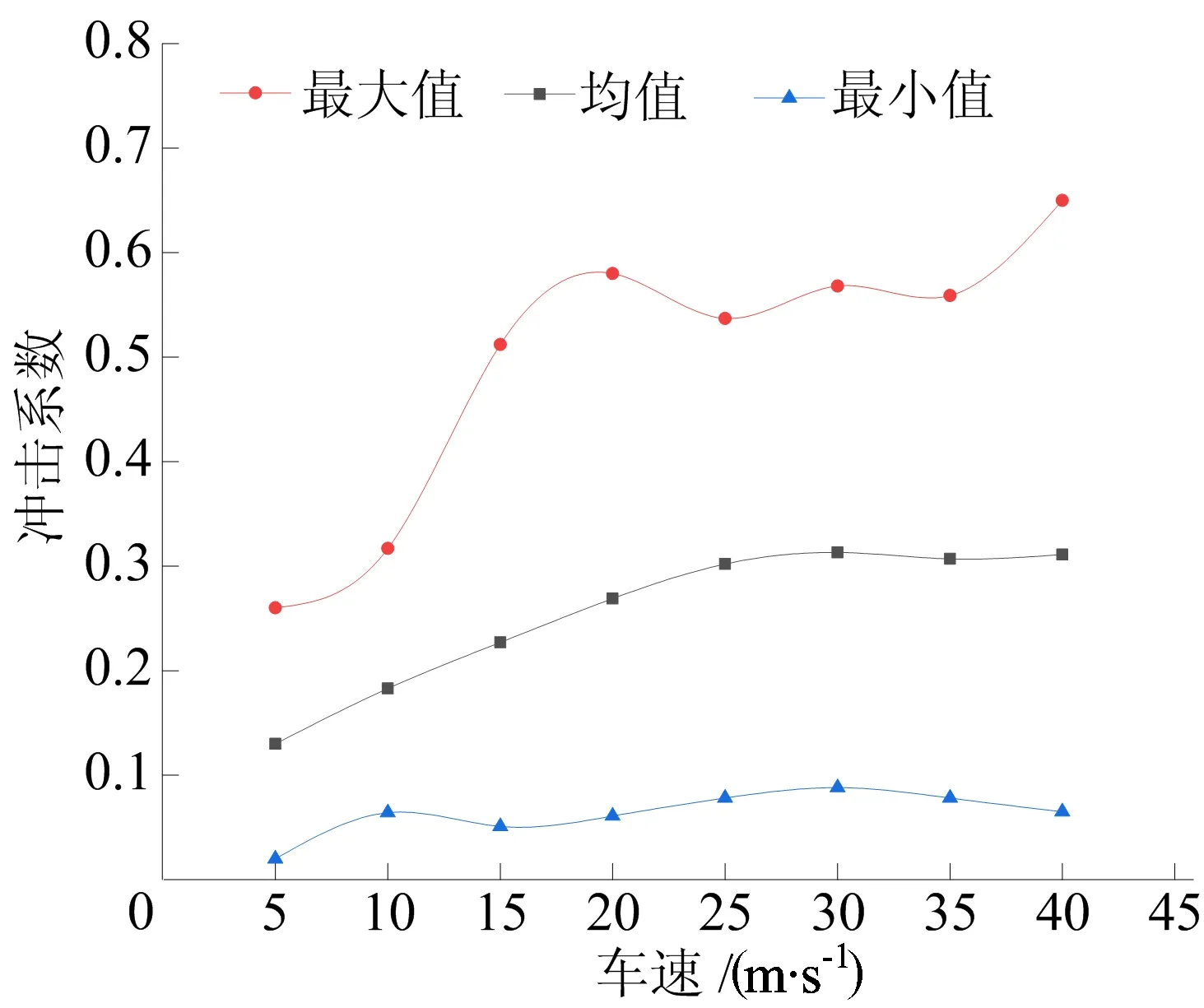
图11 不同车速冲击系数统计特征值

由图11可知,v由5 m/s增加到25 m/s,冲击系数均值由0.130增加到0.311;v较低时(v≤25 m/s),冲击系数均值随v增大线性增大,当v较高时(v>25 m/s),冲击系数均值趋于平缓,甚至有减小趋势,其原因可能是车速较大而桥梁跨径较小,车辆通过桥梁时间短,桥梁振动响应不明显。

2.4 冲击系数实测值与规范值对比分析

根据文献 [8],采用三角级数叠加法模拟桥面不平整度,研究不同车速下A、B、C 3种桥面状况等级对桥梁冲击系数的影响;通过实测桥面不平整度,分析车辆随机行驶轨迹与车辆单线程行驶条件对桥梁冲击系数的影响;将上述冲击系数与4国规范的冲击系数计算值进行对比分析,其中车辆随机行驶轨迹下的冲击系数均采用均值进行比较。冲击系数实测值与规范值对比如图12所示。

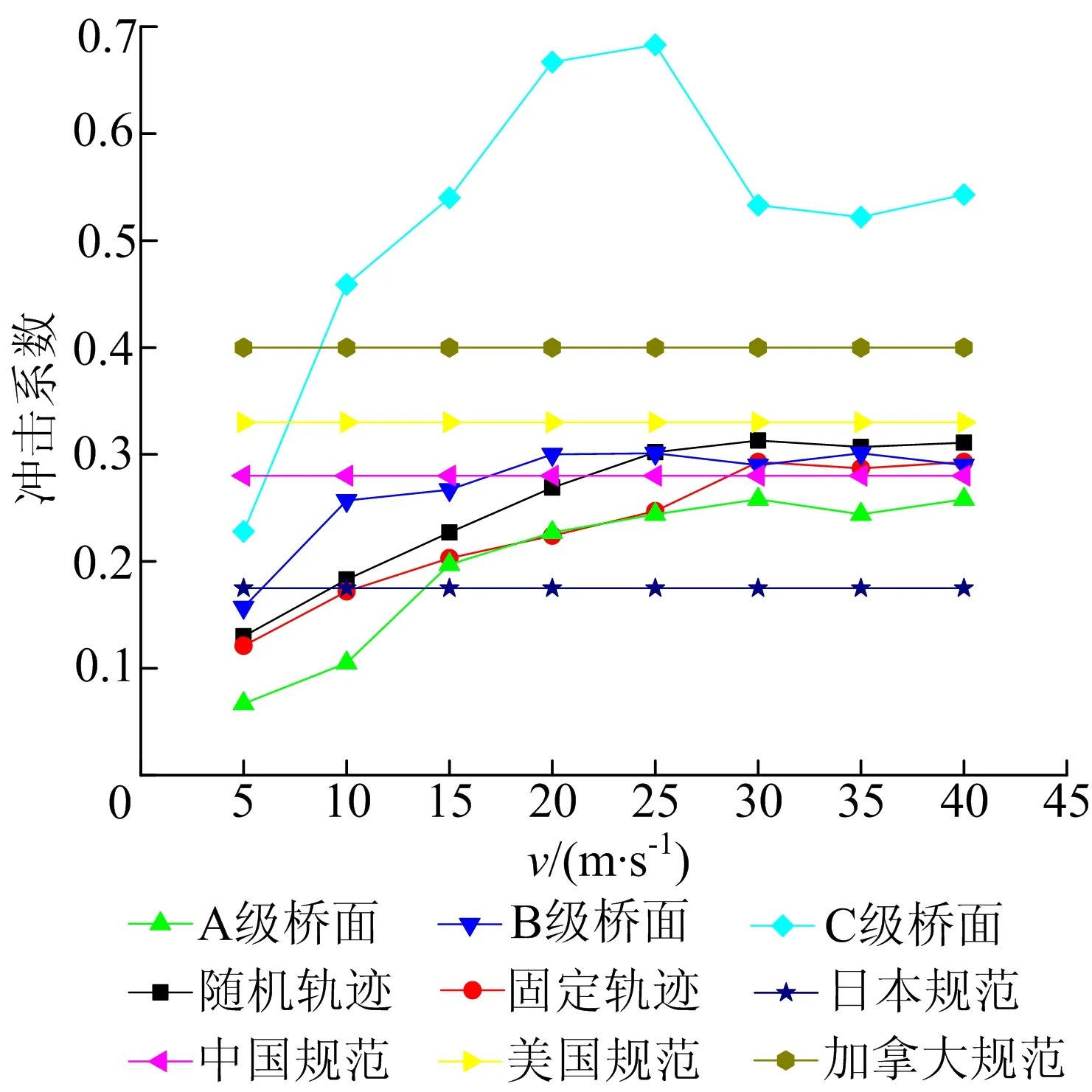
图12 冲击系数实测值与规范值对比

(1) 依据文献[8]实测、模拟不同等级桥面不平整度中,随车速增加,冲击系数整体呈增大趋势;但当车速足够大时(v>25 m/s),冲击系数增加不明显,甚至有减小趋势。同一车速下,桥面状况越差,冲击系数越大,且随车速变化越剧烈。车速较低时(v≤20 m/s),空间桥面不平整度随机行驶轨迹下的冲击系数低于相同条件下B级桥面不平整度冲击系数,说明此时按照文献[8]的规范值偏于保守;但是当车速较高时,两者接近。

(2) 通过对比单线程与车辆随机行驶轨迹桥面不平整度冲击系数可以发现,随机行驶轨迹下的冲击系数大于单线程行驶轨迹下的冲击系数,v=25 m/s时,两者的冲击系数差值最大,为0.05(20%)。由此可见,采用动载试验获得冲击系数时,为确保结果的准确,应该考虑车辆行驶轨迹的随机性。

(3) 按照文献[8]模拟A、B、C 3种等级桥面不平整度,对比所得冲击系数可以发现,C级桥面不平整度下冲击系数比A级、B级桥面不平整度下的冲击系数大,且数值整体都偏高于4国规范下的冲击系数;而A级、B级桥面不平整度下的冲击系数在车速较低时(v≤20 m/s)小于中国规范下的冲击系数,车速较高时(v>20 m/s)则相反。由此可知,桥面状况越差,冲击系数越大;按照文献[8]所得冲击系数计算值相比于美国、加拿大、日本的规范值偏于保守。

3 结 论

(1) 通过对空间桥面不平整度、车辆随机行驶轨迹同一车速下冲击系数分析可知,随着车速的增加,桥梁冲击系数逐渐增大,车速由5 m/s增加到25 m/s过程中,冲击系数均值由0.130增加到0.311。然而,冲击系数并不是随车速单调递增的,当车速达到25 m/s以上时,冲击系数趋于平稳,甚至有减小趋势。

(2) 对比随机行驶轨迹(空间)与单线程桥面不平整度获得的冲击系数可知,车辆行驶轨迹随机时所得冲击系数比单线程下的结果大;当车速为25 m/s时,两者差值最大,为20%,说明在实际桥梁动态试验中要考虑行驶轨迹对冲击系数的影响。

(3) 对比按照文献[8]中A、B、C 3种桥面状况等级下计算的冲击系数与中国规范冲击系数计算值可知,当车速较低时(v≤20 m/s),前者小于后者,车速较高时则相反;按照文献[8]所得冲击系数,相比于美国、加拿大、日本的规范值,偏于保守。

(4) 本文仅以有限数据为基础,分析了基于空间桥面不平整度车辆随机行驶轨迹下简支梁桥的冲击系数,由于速度限制,在横向的偏移不足以覆盖桥梁全宽范围,并且是否适用于连续梁等复杂体系桥梁还有待于更多的试验验证。