二元α-Bernstein-Stancu算子的逼近阶

刘 植, 刘艳玲, 陈晓彦

(合肥工业大学 数学学院,安徽 合肥 230601)

0 引 言

在函数逼近理论中,基于非负线性正算子方法构造逼近函数一直是该领域研究的重要课题之一。自1912年Bernstein提出Bernstein算子,学者们对其进行了各种推广,从而衍生出Bernstein-Durrmeyer算子、Bernstein-Stancu算子、Bernstein-Bézier算子、Bernstein-Kantorovich算子等。为了进一步优化算子的各种性能,人们对以上算子又进行了大量的研究,如对于Bernstein-Stancu算子,文献[1]研究了基于Bernstein基函数的Stancu型算子序列,得到该算子的Korovkin 型收敛定理、收敛速度的估计以及逼近性质;文献[2]研究了一类修正的Stancu型q-Baskakov-Shurder-Szász 算子,给出了加权空间下该算子的误差估计,并利用K-泛函和光滑模研究了该算子的逼近性质;文献[3]研究了Kantorovich型Bernstein-Stancu算子的Voronovskaja型渐近估计;文献[4]构造了一类修正的Stancu型q-Bernstein-Shurder-Kantorovich算子,通过光滑模和Lipschitz型极大函数估计其收敛速度,并研究了该算子的其他逼近性质。

文献[5]通过在经典Bernstein算子中引入非负实参数α的方法，构造了一类新的广义Bernstein型算子,即α-Bernstein算子。该算子具有逼近论中需要的很多优良性质,其表达式为:

(1)

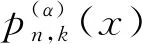
(1) 当n=1时,有

(2)n≥2时,有

特别地,当α=1时,(1)式表示的α-Bernstein算子即为经典的Bernstein算子。

近3年来,围绕α-Bernstein算子的理论研究产生了一些新的成果。文献[6]将α-Bernstein算子推广到无穷集上,得到α-Bernstein-Chlodovsky算子,并研究了其Voronovskaja型渐近估计公式等若干逼近性质。为了逼近Lebesgue可积函数,文献[7]在α-Bernstein算子基础上做了积分修正,构造了新的Bernstein-Kantorovich算子序列,称之为α-Bernstein-Kantorovich算子。利用一阶、二阶连续模研究了算子的一致收敛性以及整体、局部收敛速度,并将结果推广到二元情形。文献[8]基于Mohiuddine等的研究继续讨论了一些绝对连续函数(即导数为有界变差函数)的α-Bernstein-Kantorovich算子逼近的收敛速度问题。

算子的Durrmeyer修正是逼近Lebesgue可积函数的另一种方法。文献[9]对α-Bernstein算子进行了Durrmeyer修正,并研究了其Voronovskaja型渐近定理、整体逼近、局部逼近问题。同时,对于导数为有界变差函数的函数,讨论了其逼近的收敛速度。在上述研究成果的基础上,文献[10]进一步讨论了Bézier类和式积分型算子,并讨论了相关逼近性质。

文献[11]通过在α-Bernstein算子中引入q整数,构造了q类α-Bernstein算子,称之为 (α,q)-Bernstein算子,并得到该算子的Kovovkin型逼近定理,逼近连续函数的收敛速度以及保形性质。

为了进一步提高算子逼近的灵活性,文献[12]改变节点选择方式,研究了α-Bernstein算子的Stancu型推广,称之为α-Bernstein-Stancu算子,形式如下:

(2)

其中

0≤γ≤β;

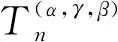
更多关于α-Bernstein算子的理论研究可参阅文献[13-14]。

本文在上述研究工作的基础上,进一步研究了α-Bernstein-Stancu算子的二元情形。首先构造二元α-Bernstein-Stancu算子的表达式,并研究该算子的Voronoskaja型定理,然后利用二元Lipschitz类得到了二元α-Bernstein-Stancu算子的逼近阶。

1 二元α-BernsteinStancu算子

N为正整数空间,N0=N∪0 {0},记

I2=[0,1]×[0,1],

C(I2)为I2上的连续函数空间,赋予范数：

‖f‖=sup|f(x,y)|。

对于二元函数f∈C(I2),0≤γi≤βi,0≤αi≤1(i=1, 2),二元α-Bernstein-Stancu算子定义为：

(3)

其中

首先,给出如下引理。

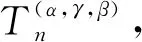
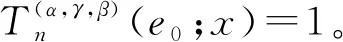
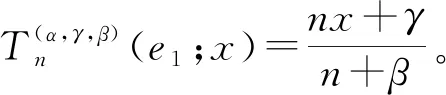
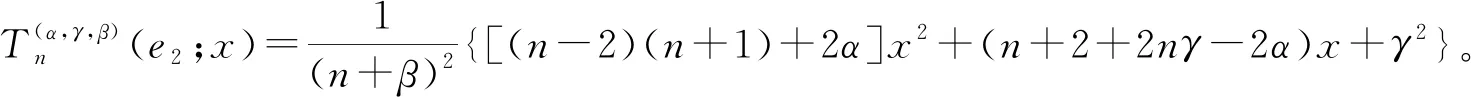
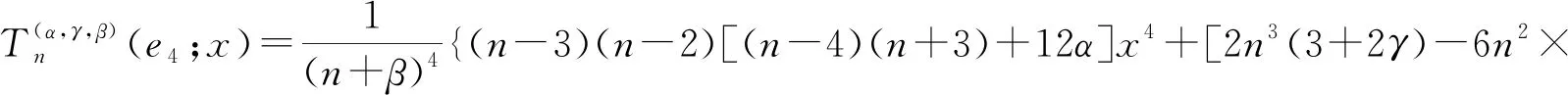
(1+2α+2γ)+4n(6αγ-4γ+24α-21)+48(1-α)(3+γ)]x3+[n2(7+12γ+6γ2)+n(29-36α-24αγ-6γ2+12γ)+2(α-1)(43+36γ+6γ2)]x2+[n2(1+4γ+6γ2+4γ3)+2(1-α)(7+12γ+6γ2)]x+γ4}。

结合引理1与二元α-Bernstein-Stancu算子(3),容易得到如下结论。

推论1记epq(x,y)=xpyq为检验函数,其中(p,q)∈N0×N0,且p+q≤4,则

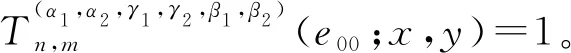
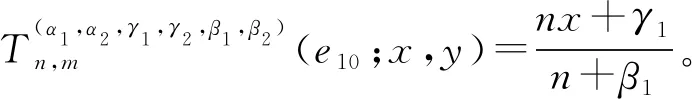
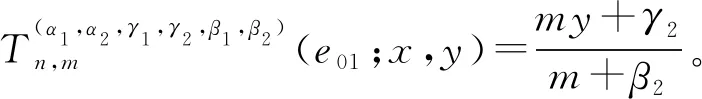
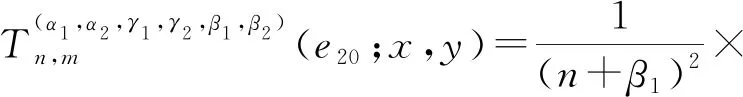
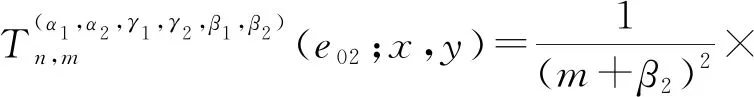
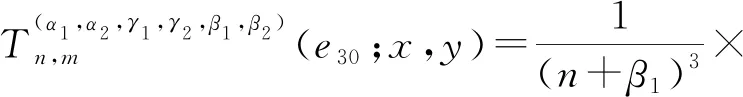
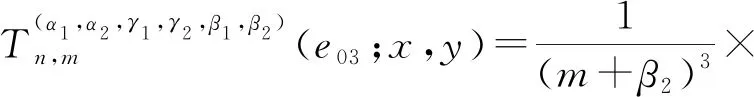
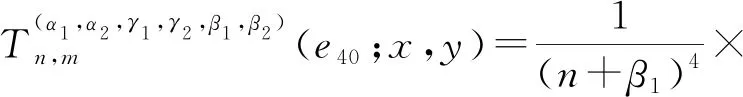
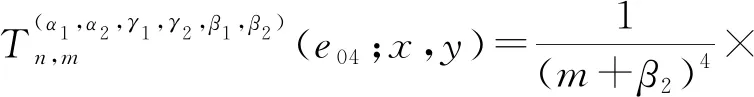
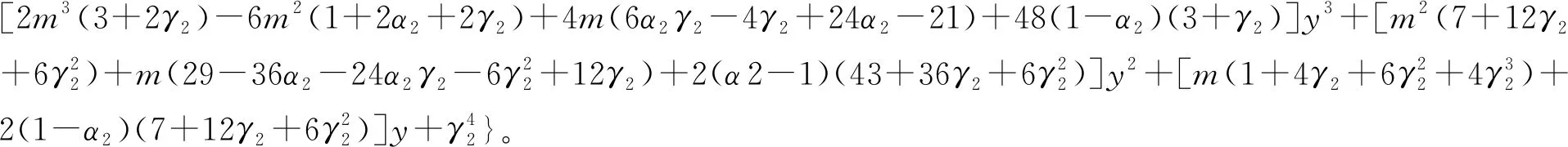
将推论1的结论直接代入，可得如下结果。

推论2对于二元算子(3)式,有

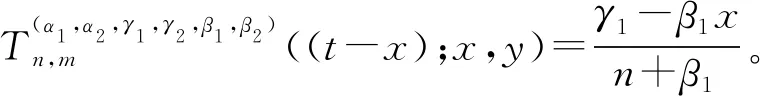
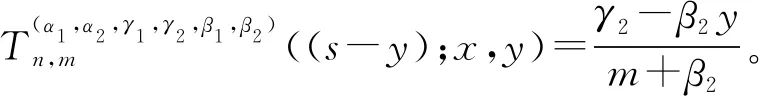
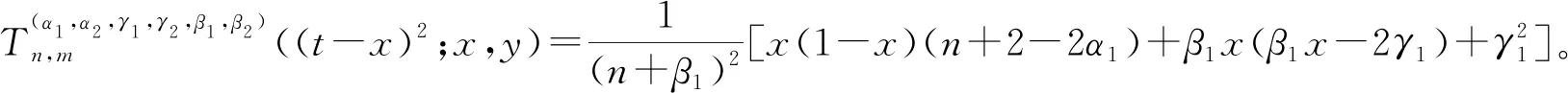
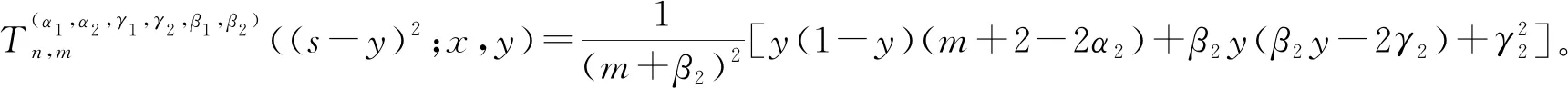
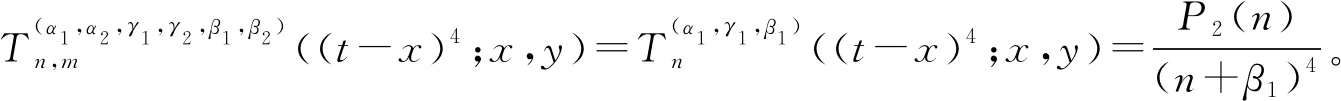
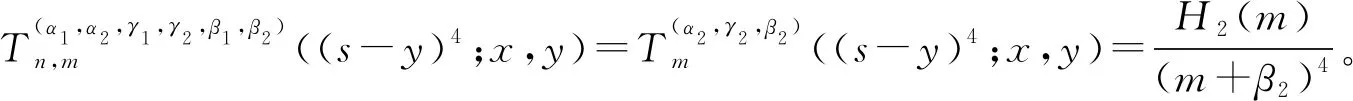
其中，P2(n)、H2(m)分别为关于n,m的二次多项式,且最高次项系数分别为3x2(x-1)2和3y2(y-1)2。

定理1 对任意函数f∈C(I2),有

证明由推论1知：

其中,(p,q)∈{(0,0),(0,1),(1,0)},以及

在I2上一致成立。由二元逼近的Korovkin型定理[15]即证。

2 逼近性质

在这一部分中,本文将讨论二元α-Bernstein-Stancu算子的Voronoskaja型定理，并通过Lipschitz类研究其逼近阶。

2.1 Voronoskaja型定理

首先,给出Voronoskaja型定理。

定理2 若函数f∈C(I2),则有:

(γ1-β1x)fx(x,y)+(γ2-β2y)fy(x,y)+

且在I2上是一致的。

证明对于(x,y),(t,s)∈I2, 由二元泰勒公式展开得:

f(t,s)=f(x,y)+fx(x,y)(t-x)+

fy(x,y)(s-y)+fxy(x,y)(t-x)(s-y)+

其中,σ(t,s;x,y)∈C(I2),且

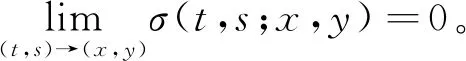
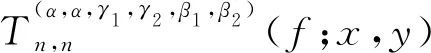
(γ1-β1x)fx(x,y)+(γ2-β2y)fy(x,y)+

(4)

注意到:

(5)

另一方面,根据Cauchy-Schwarz不等式,有

(s-y)4);x,y))1/2≤

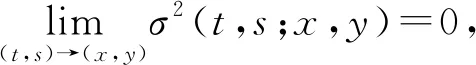
在(x,y)∈I2上一致成立。又由推论2知:

因此

(6)

将(5)式和(6)式代入(4)式即证。

2.2 α-Bernstein-Stancu算子的逼近阶

以下将利用Lipschitz类研究二元α-Bernstein-Stancu算子的逼近阶。

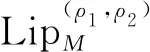
|f(t,s)-f(x,y)|≤M|t-x|ρ1|s-y|ρ2。

若记：

则有如下结论。

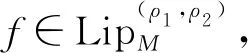
证明根据二元α-Bernstein-Stancu算子的定义及Lipschitz条件,有

令

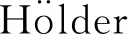
定理4 若f∈C(I2),则有：

证明对任意x,y∈I2,有

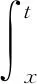
(7)

由于

再由Cauchy-Schwarz不等式知：

3 结 论

本文研究了二元α-Bernstein-Stancu算子,对于该二元算子,给出了Voronoskaja定理,并利用Lipschitz类研究了该算子的逼近阶。