一种对称无向图的同构判定算法

李正平, 白倩倩

(安徽大学 电子信息工程学院,安徽 合肥 230601)

图常用于表达抽象后的数据、信息之间的关系。在图论中,图同构是一个非常重要的课题,也是一个NP-难问题。在计算机视觉、模式识别等诸多领域中[1],图同构的判定都具有重要意义。例如，化学中同分异构体的判定、相同电路和开关拓扑的识别、相似汉字的识别等等都可归结为图同构问题[2]。

2015年,芝加哥大学的LászlóBabai教授宣称发现了一个拟多项式的图同构算法,但有学者怀疑这种算法的实际应用价值[3]。在已被认可的算法中,某些特定类型的图存在多项式算法,如树图、平面图、区间图。然而针对任意图的同构判定,目前还不存在多项式时间算法,所有的算法在最坏的情况下的时间复杂度都是指数级的。目前所提出的算法主要分为3类:基于神经网络的判定算法,如基于Hopfield网络的图的同构算法[4];基于搜索的判定算法,如Ullmann同构算法[5];基于图的特征信息的判定算法,如出入度序列法、电路模拟法[6]、特征值和特征向量法[7]等等。其中电路模拟法将图同构问题转化为电路问题,对于大多数图,可以有效快捷地得到顶点对应关系进而判定同构与否。

对于大规模对称性较强的图的同构判定问题,现有的电路模拟法效果不佳。本文提出的方法基于Dijkstra算法对原电路模拟法进行改进,适用于含权对称无向图的同构判定。

1 相关概念与原理

1.1 图同构的定义

设G1=(V1,E1)和G2=(V2,E2)是2个无向图,V表示点集,E∈V×V表示边集。若2个图同构,则存在双射f:V1→V2，当且仅当(f(u),f(v))∈E2且(u,v)与(f(u),f(v))的重数相同[8]。

由定义可知,2个图同构，即它们的结构完全相同[9],顶点之间存在一一映射的关系,且在这种对应关系下，边与边也是一一映射的。

1.2 图的邻接矩阵

邻接矩阵是图的表示方法之一,将图的结构特征描述用矩阵表示。设图G=(V,E)包含n个顶点,图的邻接矩阵D为n×n阶矩阵,其中元素分布如下:

1.3 Dijkstra算法

Dijkstra算法是一个解决单源最短路径问题的算法,它是一个迭代过程[10]。其基本思想是以源点为中心,逐步将当前路径最小的顶点加入到源点所在集合中,直到该集合包含所有顶点为止[11]。Dijkstra算法可以有效地求得图中一个节点到其他所有节点的最短距离[12],而通过顶点间的最短距离对于对称图进行顶点分类,能够降低需要交换的顶点次数,达到快速搜索的效果。d(s)=[ds1,ds2,…,dsn],dsi是源点到点i(i≠s)之间的距离。d的含义见表1所列。

表1 d的不同值所代表的含义

1.4 图同构的性质

定理1图同构的充分必要条件是具有相同的邻接矩阵[6]。

元素在邻接矩阵中排列顺序是无关紧要的。若将一个图的邻接矩阵的行与行、列与列之间进行有限次交换后与另一个图的邻接矩阵相同,则两图同构。实际上将图的邻接矩阵进行行交换和列交换就是更改图中顶点的排列顺序。

为了实现高效的判定,应尽可能根据所得顶点属性(如顶点度数、回路数等)将顶点分割成多个顶点集,各子集内的顶点属性相同，从而完成对顶点的分区。

2 判定算法

基于对称图的特殊性,利用Dijkstra算法获得的最短距离来区分顶点是便捷有效的。首先找出一组对应的顶点作为源点(这2个源点必须是已经确定对应关系的一组顶点),通常由度序列和节点电压值很容易找到一组或多组对应节点,抽取其中一组作为源点,求解其余点到源点的距离,进一步对顶点进行分区。对于中心对称图,由度序列和节点电压值不能确认任何一组顶点的对应关系,可在第1个图中任意选择1个顶点作为源点,在第2个图中遍历所有顶点找到与第1个图1源点映射的顶点作为源点。

本文算法具体步骤如下:

输入:两图的邻接矩阵。

输出:两图是否同构。

首先验证两图是否满足同构的必要条件,具有相同顶点数、相同边数和相同的重边数。

(1) 输入两图G、G′的邻接矩阵D、D′。

(2) 计算得出度序列Q、Q′,并将邻接矩阵按Q、Q′降序(升序)重排,相同则判定同构,不相同则继续判定。

(3) 将图转化为伴随电路,根据模拟电路法分别求出节点电压序列U、U′。

(4) 将邻接矩阵按U、U′降序(升序)重排并比较,相同则判定同构,不相同则继续判定。

(5) 两图中若存在电压值对应相同且异于其余各顶点的一组顶点,可初步判定为对应顶点并选作源点。将邻接矩阵中数组元素取数组中的最小值替换,值为0的元素替换为∞。根据转换后的矩阵使用Dijkstra算法得到其余点与源点的最短距离序列,转到步骤(7)。

(6) 若每个顶点电压值均为相同值,则无法确定一组对应顶点。这时,分别在第1、2个图中的最小分区(包含相同电压值顶点最少的顶点子集)中选取一个顶点作为源点,通过Dijkstra算法求解最短距离序列。

(7) 根据最短距离序列得到两图顶点映射关系,根据顶点映射关系调整邻接矩阵,相同则两图同构,不相同则两图异构。

3 实例说明

电路模拟法判定两图同构最坏的情况是对称图,需对顶点次序进行全排列,即邻接矩阵需做n!次调整。

例1假设要判定的图为G、G′，如图1所示。

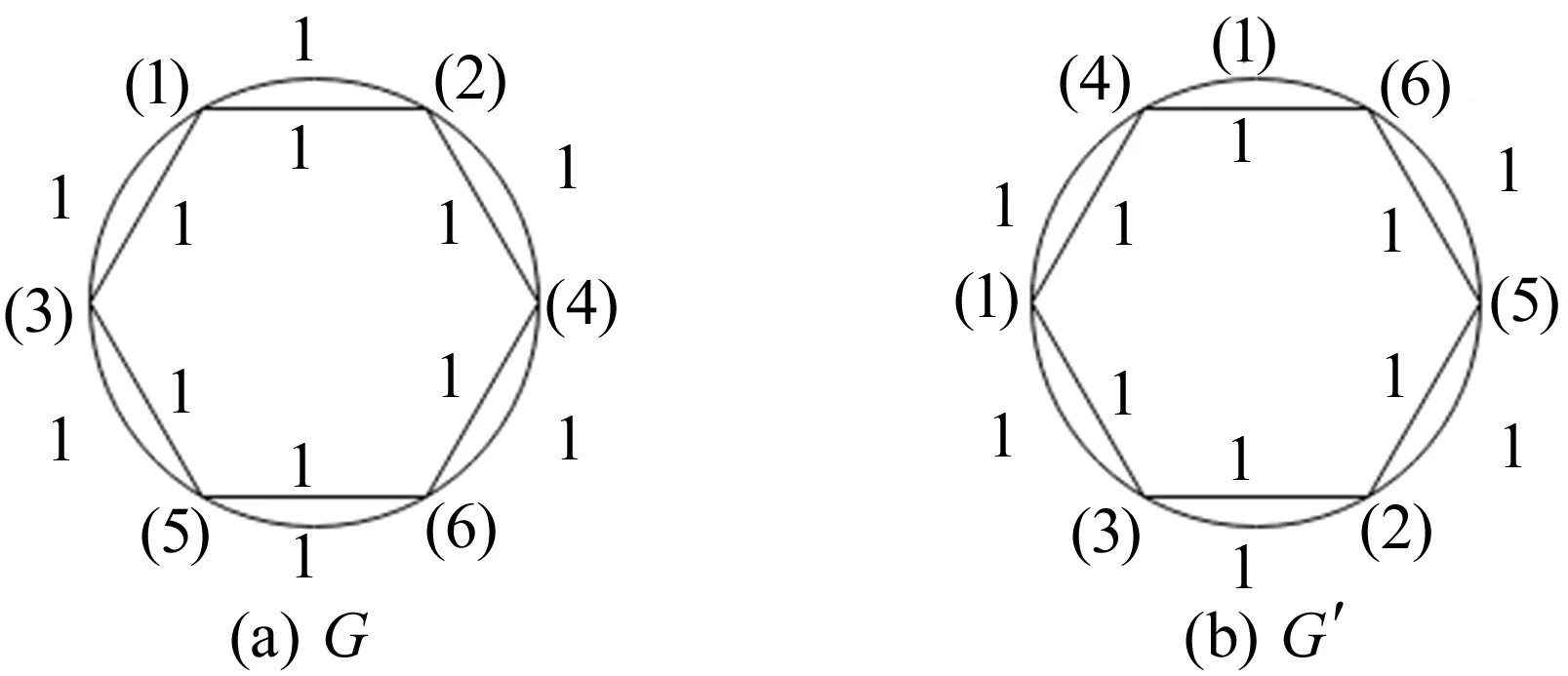
图1 对称无向图同构实例

(1) 输入两图的邻接矩阵D、D′。D、D′为：

(2) 分别计算出两图的度序列Q=[4,4,4,4,4,4]、Q′=[4,4,4,4,4,4]。度序列相同则可能同构,将2个度序列按降序排列均为[4,4,4,4,4,4],因为图1中各顶点度均相同,所以无法按照度序列对顶点分区。

(3) 分别求出两图的导纳矩阵。N、N′为：

增加额外的顶点v7、v7′,并将其作为激励参考点。利用电路模拟法求出两图节点电压序列：

U=[0.500 0,0.500 0,0.500 0,0.500 0,

0.500 0,0.500 0)],

U′=[0.500 0,0.500 0,0.500 0,0.500 0,

0.500 0,0.500 0]。

(4) 对两图节点电压序列按降序重排均为[0.500 0,0.500 0,0.500 0,0.500 0,0.500 0,0.500 0],无法根据电压值对顶点分区。

(5) 将两图的邻接矩阵D、D′做以下调整，用于Dijkstra算法运算,即

得到新的邻接矩阵：

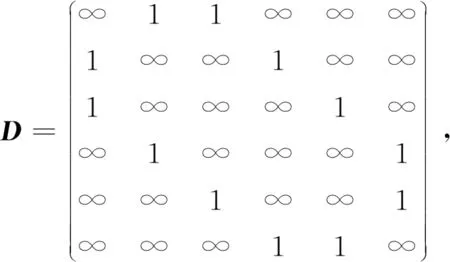
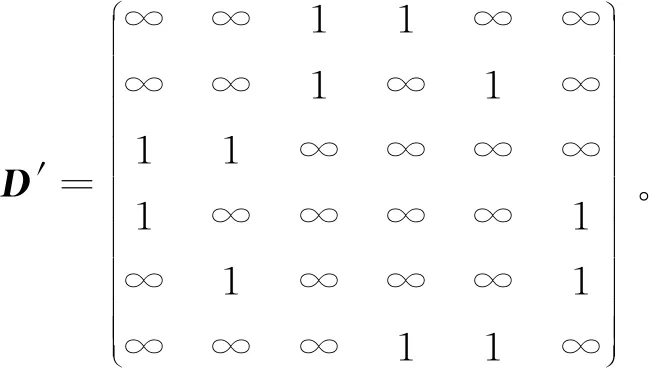
(6) 任取图G中的一个顶点如v1作为源点,通过Dijkstra算法得出最短距离矩阵d(1)=[0,1,1,2,2,3],矩阵各元素对应顶点(v1,v2,v3,v4,v5,v6)。对于图G′,任一顶点作为源点的距离矩阵均为d′(i)=[0,1,1,2,2,3] (i=1～6), 各元素对应顶点为(v1′,v3′,v4′,v2′,v6′,v5′)，因此所有顶点均有可能是图G中v1的对应顶点。依次选取图G′中的点作为源点与图G′尝试匹配，如v1→v1′时的顶点分区及可能对应关系(v2,v3)→(v3′,v4′)、(v4,v5)→(v2′,v6′)、v6→v5′。

(7) 重复排列所有可能的顶点对应关系,比较对应的邻接矩阵,直到得到一组映射关系(v1→v1′,v2→v4′,v3→v3′,v4→v6′,v5→v2′,v6→v5′),使邻接矩阵相同,图G、G′同构。若根据所有可能的顶点对应关系调整后的邻接矩阵都不相同,则判定两图异构。

4 算法对比分析

基于图同构的性质提出的顶点置换法,其思路是对图中顶点顺序进行全排列,验证两图的所有可能的邻接矩阵中是否存在相同矩阵。因为随着图的规模的增大,交换的次数很庞大,并且判定两图异构时需要比较全部的排列可能才能得出结论,所以只适合于小图的同构判定。而原电路模拟法利用各节点电压对顶点进行分区,大大减少了顶点映射搜索范围。但是对于对称图,各顶点度数相同且电压相同,各顶点自身不变属性相同无法区分顶点。此时该算法优势消失,时间复杂度几乎接近顶点置换法。本文提出的算法利用顶点之间的距离关系可有效地对对称图顶点进行分区,进而有效提高同构判定的效率,相对于顶点置换法和原电路模拟法,具有更高的效率。

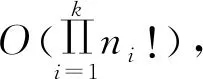
针对本例中图G,通过需要交换的顶点分区情况对几种方法的搜索范围进行比较:

(1) 顶点置换法。需置换所有顶点的排列方式,搜索范围6!=720。

(2) 度序列法和模拟电压法。度和节点电压并未对顶点做出分区,搜索范围同顶点置换法为6!=720。

(3) 本文算法。加入Dijkstra算法所得距离序列后,搜索范围为6×2!×2!=24。

5 实验结果分析

为了验证本文算法的效率,分别选取不同顶点(3～160)的对称无向图进行同构判定实现,与原电路模拟法进行对比，结果见表2所列，如图2所示。测试环境如下:CPU为Intel(R) Core(TM) i5-2400 CPU @ 3.10 GHz 3.10 GHz;内存为4.00 GB;操作系统为Windows 7;编程语言为Matlab。

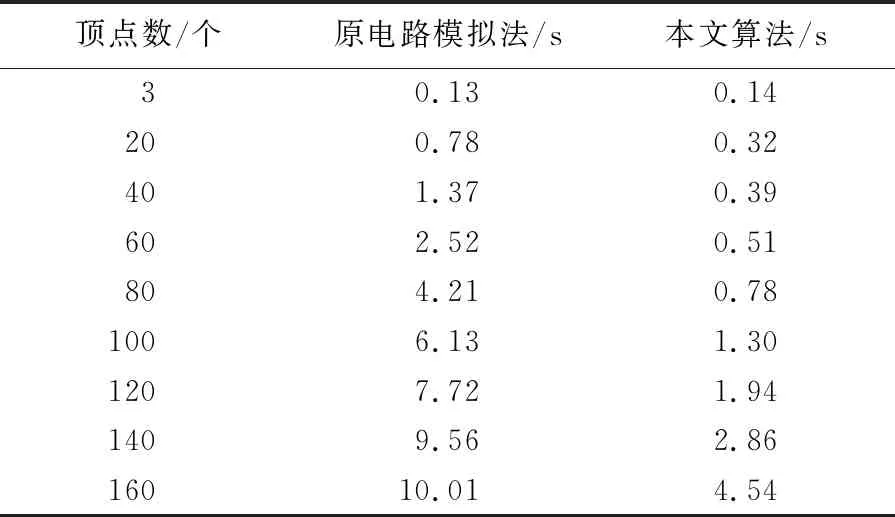
表2 不同算法判断对称无向图同构的运行时间

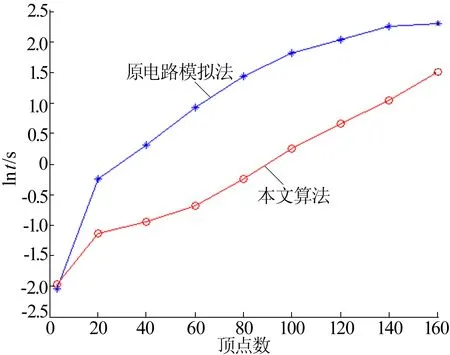
图2 对称无向图同构判定不同算法的运行时间比较

对于强对称性图的同构判定,电路模拟法的仿真时间主要消耗在对两图邻接矩阵的转换和匹配上。而本文算法通过加入距离矩阵减少了搜索范围。从图2可以看出,在电路模拟法中加入Dijkstra算法后可以有效地降低算法的时间复杂度,表明该算法对于强对称无向图的同构判定是有效的,并且顶点数越大,两算法的时间复杂度差异越大,即本文算法的优化效果越明显。

6 结 论

本文提出的对称无向图同构判定算法,是基于Dijkstra算法对电路模拟法判定算法的优化。由于对称无向图中多个顶点具有相同电压,局部排列的规模就会变大,此电路模拟法的优势逐渐削弱。改进算法后,提高了对称性较高的图的算法实用性,对于电路模拟法出现故障的情况得以解决。通过Dijkstra算法缩小对应顶点的搜索范围,减少邻接矩阵的比较次数,提高了对称无向图的判定效率。基于图的特征信息的同构判定算法的基本思路是一致的,首先对顶点进行分区,然后根据“两图同构的充分必要条件是具有相同的邻接矩阵”来最终判定两图是否同构。找到一个简洁有效的充要条件是该领域未来的一个研究方向。