不完全层次分析法在民俗村项目决策中的应用

王振华，张为元，闫丽宏

（咸阳师范学院数学与信息科学学院，陕西咸阳 712000）

随着人们经济收入的增长，人们对旅游产品、项目等的要求越来越高了，相对于传统的观光娱乐型旅游，人们越来越倾向于那些更具文化、互动和探索的旅游。在此背景下，质朴、神秘、富有浓烈的文化气息的民俗村备受追捧。民俗旅游是一种具有可参与性的文化旅游，是一种更高层次的旅游[1]。就目前来说，民俗旅游在旅游业中占有相当大的比重。据数据统计，旅游者中有59.8%的游客最感兴趣的是各地区的风土人情，民族生活方式[2]。近几年政府对传统民俗文化越来越重视，民俗村、民俗园、民俗博物馆等民俗旅游区层出不穷，民俗村旅游业的发展具有巨大市场潜力。

民俗旅游资源是民俗旅游产业赖以发展的基础，吴金林等[3]认为民俗旅游资源是指能够为旅游开发者所用，具有较高的旅游价值，能够吸引旅游者前往观赏，并可以产生经济利益的民风和风俗等资源。民俗旅游资源的开发能给地方带来巨大的经济效益，同时对当地的就业、发展也有不可估计的推动作用。面对如此广阔的市场，其行业竞争必然激烈。要想在民俗村的开发建设中脱颖而出，最重要的就是要提前做好旅游项目规划，确定资源开发的正确排序，从而确定旅游发展的正确方向，避免走弯路、走错路。

项目规划是推动民俗村建设又好又快发展的基础。6 个民俗资源目：农家乐、古民居、民俗展、农业园、庙会、民间表演，遵循项目选择的4 个标准：观赏性、娱乐性、参与性、文化性，通过不完全层次分析法解决了某民俗村规划中各民俗项目的排序问题，让最有市场前景的项目优先开发，从而实现了资金的最优配置。

层次分析法[4]是一种定量与定性相结合，层次化和系统化分析复杂问题并且利用计算机快速做出最佳决策的方法。层次分析法一般把问题分解成目标层，准则层，方案层，不完全层次结构就是指准则层中的一个因素，只支配措施层的一部分因素，这种层次结构称为不完全的。层次分析法优点：①系统性：即把研究的对象看做一个系统。②有效性:可适用于非结构化的复杂的问题，或者是有许多个目标，多个准则，多个时间段等各种问题的分析与决策。③实用性：这种方让让决策者直接与决策分析者彼此了解，决策者在某种紧急情况下就可直接应用它。层次分析法的应用已经遍及现实生活中的许多方面例如：城市建设，交通运输，旅游开发，军事管理，教育建设，社会经济发展等许多领域[5-9]。

1 预备知识

1.1 不完全层次结构

对于准则集合A中的任意元素a，表示方案集合B中受a支配的元素，令这里a→表示a支配，显然有B0⊆B。

定义1如果在一个层次结构中存在a∈A使得B0≠B那么就称这个结构为不完全层次结构。不完全层次结构就是指准则层中的一个因素，只支配方案层的的一部分因素。

1.2 构造成对比较矩阵

定义2如果成对比较矩阵中的元素满足aij＞0，aij=，i,j=1,2,…,n，那么就称A为成对比较矩阵或互反矩阵，aij的含义见表1。

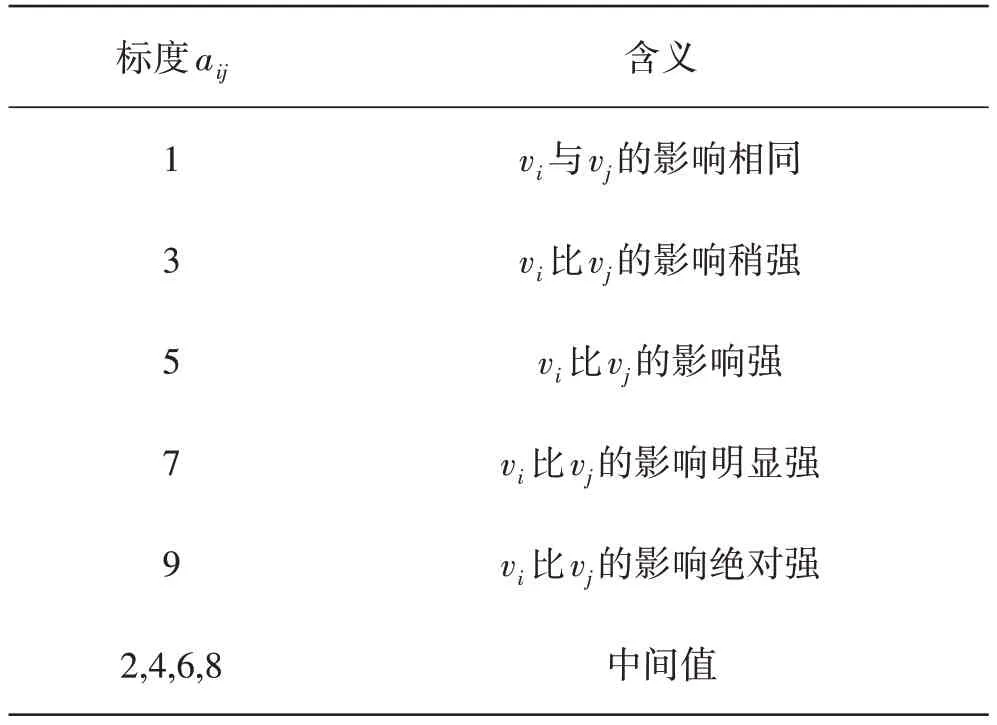
表1 1～9尺度aij的含义

1.3 矩阵一致性检验

定义3如果成对比较矩阵A满足aij=aik·akj，i,j,k=1,2,…,n那么就称A为一致性矩阵。

定理1设A是n阶成对比较矩阵，λmax为A的最大特征根，则λmax≥n；当且仅当λmax=n时A为一致性矩阵。[10]

计算每一个成对比较矩阵的最大特征根及对应特征向量，利用下列指标做一致性检验；若从第二层开始每层都通过一致性检验，则特征向量归一化后就得到该层相应的权向量；最后，计算最下层对目标的权向量，并按照组合权向量对方案决策。一致性检验的步骤如下[11]：

第1步，计算一致性指标

第2步，从表2选择相应的随机一致性指标RI

第3步，计算一致性比率

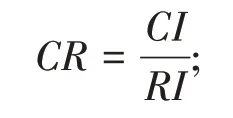
第4步，第P层组合一致性比率

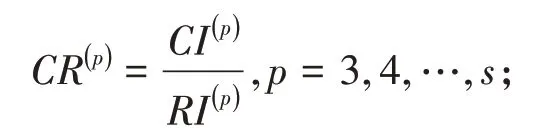
第5 步，最下层（第s层）对第1 层的组合一致性比率为

当CR＜0.1 时，比较矩阵A是一致性矩阵；当CR≥0.1 时，就需要把矩阵A修正成一致性矩阵。第p层通过一致性检验的条件为CR(p)＜0.1，只有当CR*＜0.1 时，才认为整个层次结构的比较矩阵通过一致性检验，只有这样，最终的组合权向量才可作为决策的依据，平均随机一致性指标RI的值见表2。

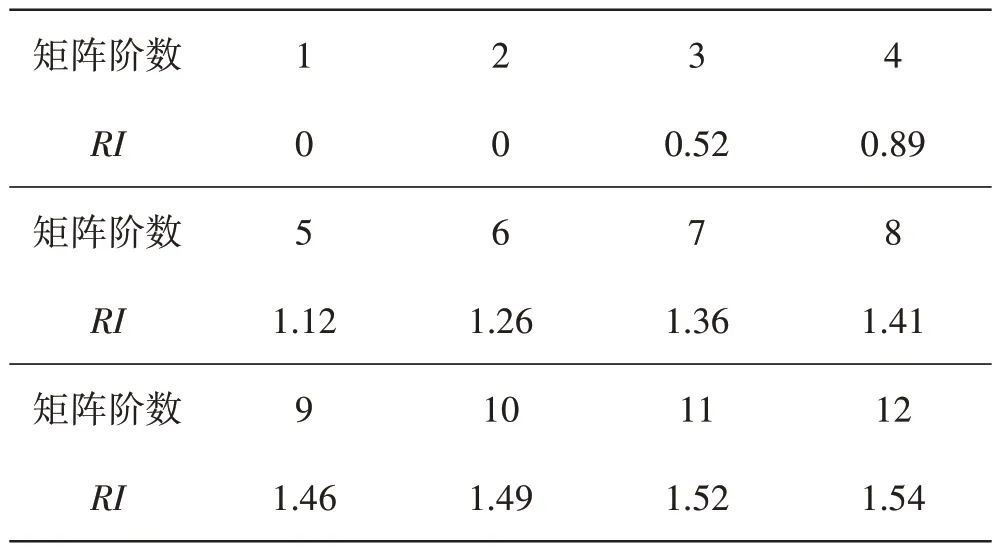
表2 平均随机一致性指标RI的值

1.4 不完全层次结构中的残缺矩阵

当无法对某两个因素进行对比时，成对比较矩阵A=(aij)就会出现残缺，为了修正残缺矩阵A=(aij)，一般采用的方法如下[12]：

其中θ表示比较矩阵A中的残缺项，mi为第i行θ的个数。

2 民俗村建设项目规划

2.1 模型建立

民俗村，就是以特色实现旅游功能的村落。最重要的就是要做到突出地方特色，保护特色建筑、打造特色旅游项目、推出特色餐饮、开发特色旅游商品，让游客住得有特色、玩得有特色、吃得有特色、买得有特色。为了充分发挥民俗旅游的效用，各地在开发民俗旅游资源时要遵循一些原则，这样在开发中才能少走弯路，实现价值最优化。通过对民俗文化村项目的深入分析，我们建立了图1所示的不完全层次结构，第三层有三个因素（农家乐、古民居、农业园）不受第二层中文化性的支配。

目标层：民俗村项目规划；

准则层：观赏性C1、娱乐性C2、参与性C3、文化性C4；

方案层：农家乐P1、古民居P2、民俗展P3、农业园P4、庙会P5、民间表演P6。

2.2 模型求解

第1 步，准则层的成对比较矩阵及一致性检验。如果要比较准则层4 个因素“观赏性，娱乐性，参与性，文化性”对民俗村项目规划这个目标的影响，就需要做=6次对比，得到成对比较矩阵

可以计算得到A的最大特征根为λmax=4.118，λmax对应的归一化特征向量

ω(2)=(0.434,0.068,0.086,0.413)T，

准则层的一致性指标

由表2查得随机一致性指标

RI(2)=0.90,

一致性比率

所以矩阵A通过一致性检验，ω(2)可以作为第2层对于第1层的权向量。

第2步，方案层的成对比7较矩阵及组合权向量。

上面Bk,(k=1,…,4)中的元素是方案Pi与Pj针对准则Ck的重要性之比。其中B4含有残缺项θ，当θ不在残缺矩阵的主对角线上时，就用零来修正B4中的θ，修正后的B4为，

然后我们分别求出成对比较矩阵B1，B2，B3，的最大特征根λk相应的归一化特征向量，指标CIk及RIk，这里k=1,…,4 本案例准则层含有4 个因素，决策层含有6个因素。第2层对第1层的权向量为

ω(2)=(0.434,0.068,0.086,0.413)T,

第3层对第2层的权向量为

这里，我们构造矩阵

则方案层对目标层的组合权向量为

ω(3)=W(3)w(2)。

由成对比较矩阵B1，B2，B3，的最大特征根λk及其相应的归一化特征向量得到表3。

定义4如果矩阵A的最大特征根是单根入，且入对反正的特征向量ω，即ω的所有分量为正数，那么就称A为正矩阵。

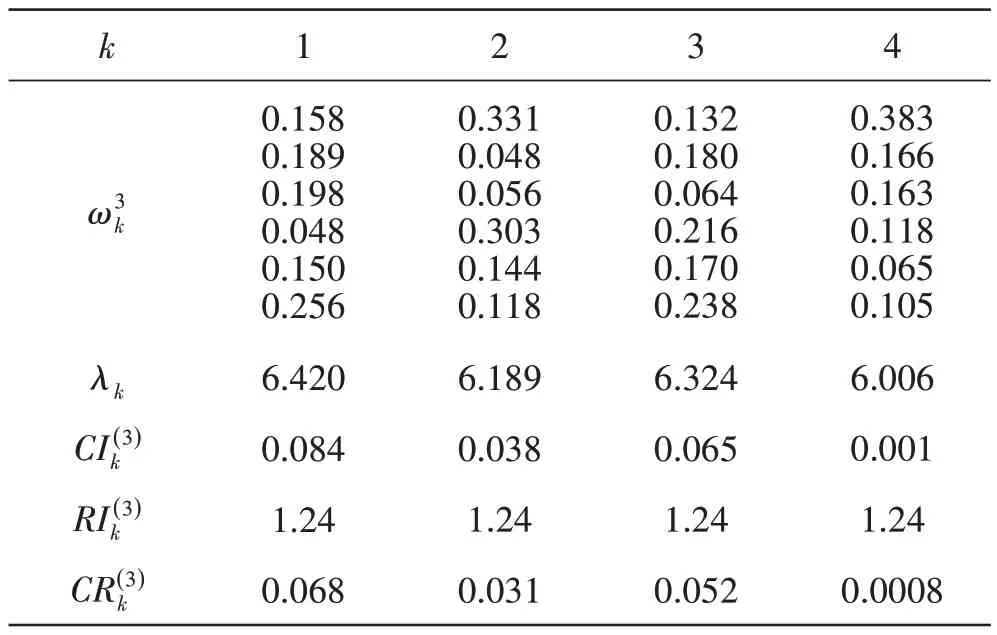
表3 第3层的计算结果

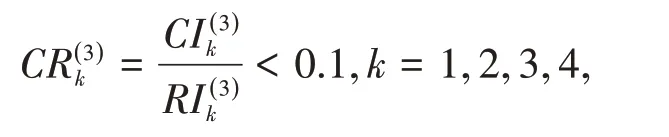
所以B1，B2，B3，都是正互反一致矩阵。由表3 中的数据我们得到

这样就得到方案层P1,P2,P3,P4,P5,P6对目标层的权重分别为0.261，0.169,0.163,0.109,0.116,0.182，所以六个方案由优到劣的排列顺序依次为

P1＞P6＞P2＞P3＞P5＞P4。

第3步，组合一致性比率检验。在应用层次分析法做重大决策时，必须要进行组合一致性检验，以保证组合权向量作为最终决策依据的可靠性。方案层（第三层）对目标层（第一层）的组合一致性比率为

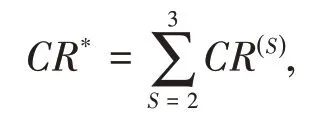
现在，只需要验证CR*＜0.1 就行了。已知CR(2)=0.04，下面求解CR(3)的值。

由表3和向量ω(2)计算得到

因为CR(3)＜0.1 所以方案层通过组合一致性检验。于是第3层对第1层的组合一致性比率为

CR*=CR(2)+CR(3)=0.056＜0.1,

因为CR*充分小，所以方案层对目标层的组合一致性检验通过。

第4步，结果分析。因为整个层次的比较矩阵全部通过一致性检验，所以ω(3)能做为决策的依据。于是六个方案由优到劣依次为

P1＞P6＞P2＞P3＞P5＞P4。

其中P1项目最适合开发，P4项目相对而言最不适合发展。

3 结论与建议

民俗村开发对于农村的生产发展，农民收入，生活改善，文明乡风形成，整洁村容建设等，都具有重要的作用。层次分析法在现实应用中有缺陷，首先决策者的主观态度对结果影响大，其次它不适用于对精确度要求较高的问题。但是层次分析法在处理许多定性与定量相结合的复杂决策问题时却非常高效，而且层次分析法在现实生活中的应用已经非常广泛。现在，关于民俗村开发策略给出如下建议：P1,P6,P2是3 个要优先发展的项目，P3,P5与P4在开发顺序中排在后面，可酌情开发。

P1农家乐：推出传统特色餐饮，让游客看到美食的制作过程。比如陕西的各种农家小吃：麻花、油茶、搅团、油泼辣子、茯茶、廖化糖、陕北馃陷、琼锅糖、空心挂面等等。

P6民间表演：展示各种民俗表演，吸引游客积极参与。比如皮影戏、地方戏、民间杂技、踩高跷、舞狮、舞龙、跑旱船、吹糖人等等。

P2古民居：利用古村落建筑的魅力吸引游客。维持古民居的原汁原味、古色古香，对古村落人文环境和自然生态加以保护。

P3民俗展：展示与民俗息息相关的各种艺术形式，比如剪纸、泥塑、面塑、民间美术、剪纸、皮影、绣花、染织、年画、壁画、陶瓷、雕刻等等。

P5庙会：带有宗教色彩，不能同时满足不同游客的需求。

P4农业园：现在每座城市的周边都有农业大棚，这对游客而言已经习以为常，缺乏吸引力。