基于EMD和SVM的铁路客运量分析研究

张 鹏，张海燕

（太原工业学院理学系，山西太原 030008）

人们生活水平的提高使得火车、高铁等出行工具的受众范围越来越广。对铁路客运量的预测也显得尤为重要。铁路客运量的预测能够让铁路部门更好地统筹规划，也能让其他行业提前对出行高峰做出准备。很多国内外的学者用各种方式对铁路客运量进行了预测，例如BP 神经网络、支持向量机、灰色线性回归、新型组合模型等[1]。将基于“先分解后集成”的思想[2]，采用EMD 和SVM 结合的预测方法来对铁路客运量进行分析研究。

1 原理介绍

1.1 经验模态分解

在实际中很多时间序列都不具有稳定性，仅使用支持向量机进行回归和预测，精度往往不如人意。将引入经验模态分解来提高精度，EMD 模型是可以把复杂信号拆成有限的IMF 分量和余项[3-5]。EMD 分解要满足两个假设：首先，信号要有极大和极小值；其次，数据局部时域特性由极值点间时间尺度唯一确定。步骤如下：

（1）识别出信号x(t) 全部的极大值点和极小值点；

（2）使用3 次样条曲线对信号x(t) 的极值点的做拟合，得到x(t)的上下包络线esup(x)、einf(x)，其中，有如下的关系式：

（3）计算上包络线esup(x)和下包络线einf(x)的平均值a(t)，其中，

（4）用信号x(t)减去平均值a(t)可以得到一个新的函数y(t)，其中，

（5）判断y(t)是不是IMF 分量，依据是IMF 的两个特点，如果y(t)满足IMF 的两个特点，就可以记y(t)是信号的一个IMF分量w1(t)；

（6）假如y(t)不满足IMF 的两个特点，就要用新的y(t)；

（7）重复上述步骤直到y(t)满足了IMF 的特点，记y(t)是x(t)的一个分量w1(t)；

（8）根据上述步骤每得到的一阶IMF，从x(t)中减去它，得到一个新的函数b1(t)，

（9）将新得到的b1(t)作为新的x(t)，重复上述步骤，得到其余IMF 分量w1(t)，直到rn(t)比预定值小或者成为了单调的函数，就停止分解，记最后的bn(t)为残余分量。

经过上述的EMD 分解方法，就将原始信号x(t)分解成了n个IMF分量和残余分量的线性叠加，即

1.2 支持向量机

支持向量机是在深度学习被提出来前表现较好的机器学习算法。SVM[6-8]的基本思想是：用内积函数定义非线性变换，将输入空间从低维变到高维空间中，使样本线性可分。

{(x1,y1),(x2,y2),(x3,y3),L,(xn,yn)}作为一个训练集，其SVM估计为：

在公式（6）中，＜·＞代表的是w和φ(x)的内积的运算，φ(x)代表的从输入空间为高维特征空间的非线性映射，w表示的是权系数向量，c是一个常数。其正确性的衡量采用的是损失函数，在SVM 模型的回归中，采用的是不敏感损失函数，公式如下：

w和c的确定的依据是风险最小化原则，它的优化公式如公式（8），其中C表示的是惩罚因子，

为了能够找到这两个系数，还需要引入两个松弛变量——ξi、ξj，优化公式为：

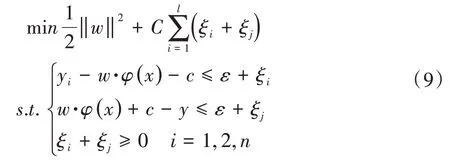
依据拉格朗日方法，求到w的鞍点，其中，αi，是拉格朗日乘子：

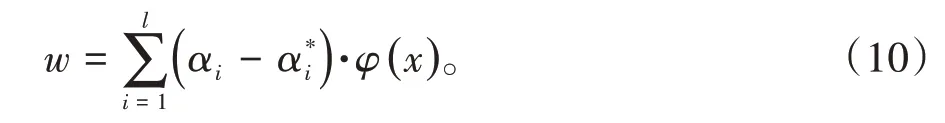
将式（10）代入式（6）中，可以得到（11），其中k(xi,x)称为是核函数，

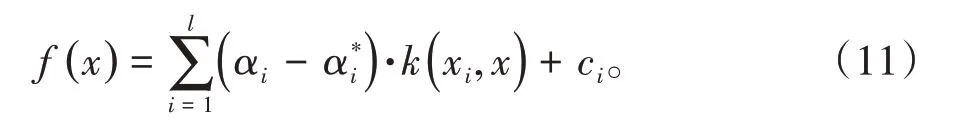
优化（9）式的，可以将它转化成为对偶问题。利用对偶定理，得到如下的对偶式：

依据KKT条件，可以求出αi，，期间会有部分αi，的值不等于零，其对应的样本，称为支持向量。

2 实例分析

2.1 数据及模型评价标准

数据选自国家统计局2011年10月到2020年1月的铁路客运量。具体的铁路的客运量数据如表1 所示，鉴于数据过多，这里只展示部分。

表1 铁路客运量当期值

将使用平均绝对百分误差（MAPE）和相对误差（Pe）来衡量所建立的模型的回归和预测能力，当MAPE 小于5%，测试集的Pe大部分小于10%，则认为建立的模型达到了精度要求。其中：

2.2 经验模态分解

对上述的铁路客运量数据进行经验模态分解，将其分解成了3 个IMF 分量和一个剩余分量。使用matlabR2016a进行分解，结果如图1所示。

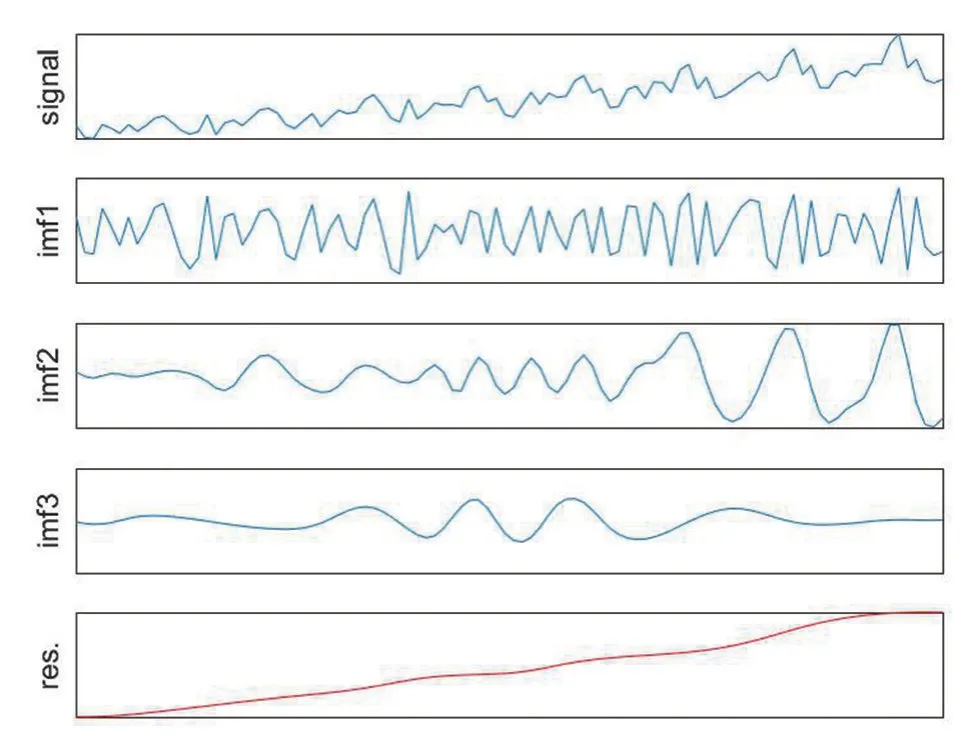
图1 铁路客运量样本数据及EMD分解结果

从图1中可以看到，铁路客运量数据被分解成立三个IMF分量以及一个残余分量，分解得到的模块具有一定的规律性且是平稳的时间序列。

2.3 数据预处理

把样本数据归一化处理，可以使模型以更快速度求得最为优异的结果。采用的映射如下：

运用上述公式分别对EMD 得到的三个IMF 分量和剩余分量进行归一化处理。为了方便叙述，把100个样本按时间赋予一个编号t，归一化后数据如表2所示。由于数据过多，仅展示部分数据。

表2 EMD分解结果

在使用SVM进行回归预测时，需要把100个样本区分为训练集和测试集，利用训练集来进行模型训练，利用测试集来检验模型预测的精度。由于数据是时间序列，所以将前70个月份的数据作为训练集，后30个月的数据作为测试集。

2.4 参数寻优

使用GA 来寻找SVM 中参数的最优值，初始化参数最大额进化代数为200，种群最大数量为20。先设置参数的变动范围，分别对使用EMD 分解得到的三个IMF 分量和一个剩余分量的参数使用GA 遗传算法进行参数的寻优[9-11]。输入为滞后3 个月份的分量值，标签为当月的分量值。运行遗传算法，得到各分量的最优参数如表3所示。

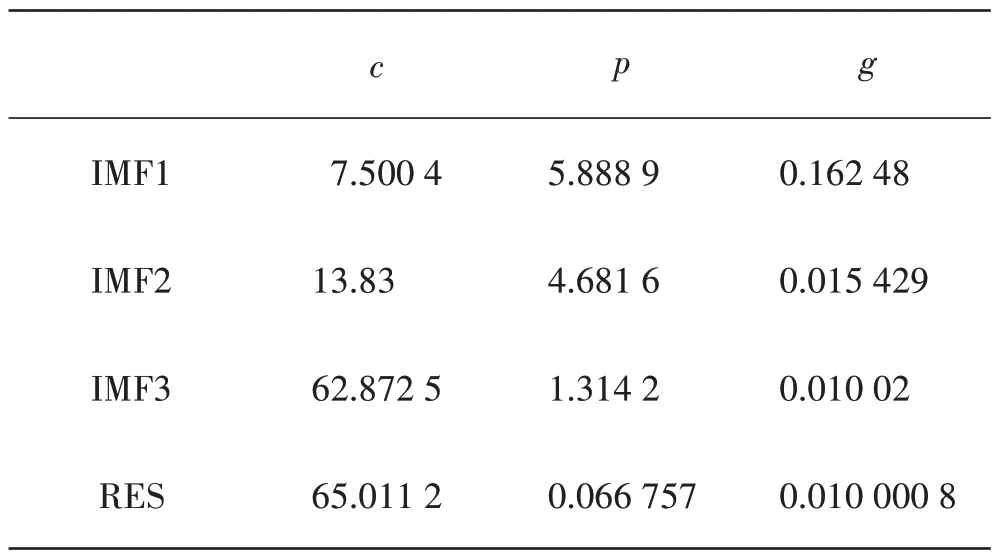
表3 最优参数

2.5 分量的回归与预测

分量的回归与预测使用的是RBF 核函数，使用matlabR2016a进行回归与预测。基本的思想是：对各个分量进行单独的回归与预测，将训练集中滞后3个月份的分量值的归一化后的数据作为输入，将训练集中当月的铁路客运量的归一化数值作为输出，对模型进行足够的训练，得到各个分量的分量值与铁路客运量之间的归一化数据的非线性映射。各个分量的回归结果和预测结果如图2～5所示。

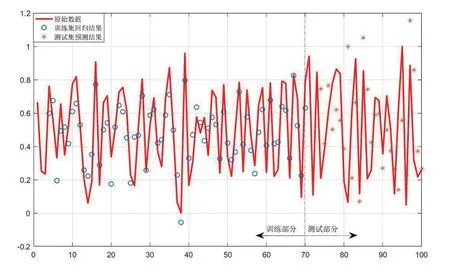
图2 分量IMF1的回归及预测结果

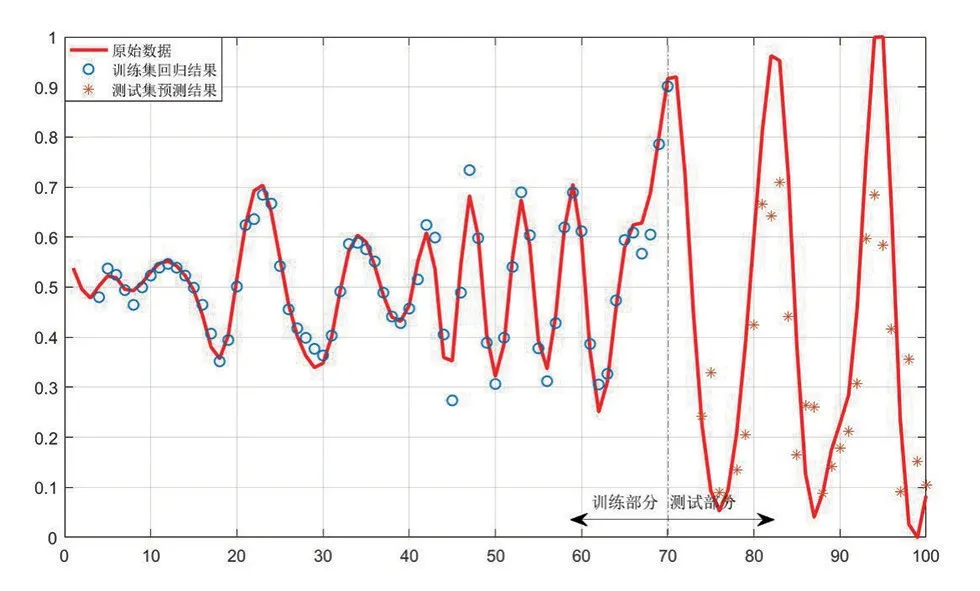
图3 分量IMF2的回归及预测结果

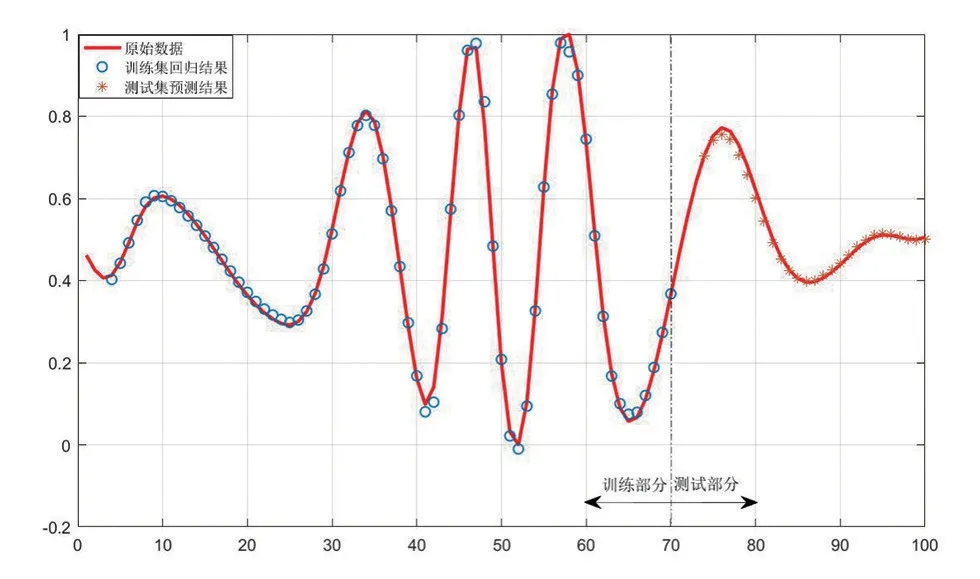
图4 分量IMF3的回归及预测结果

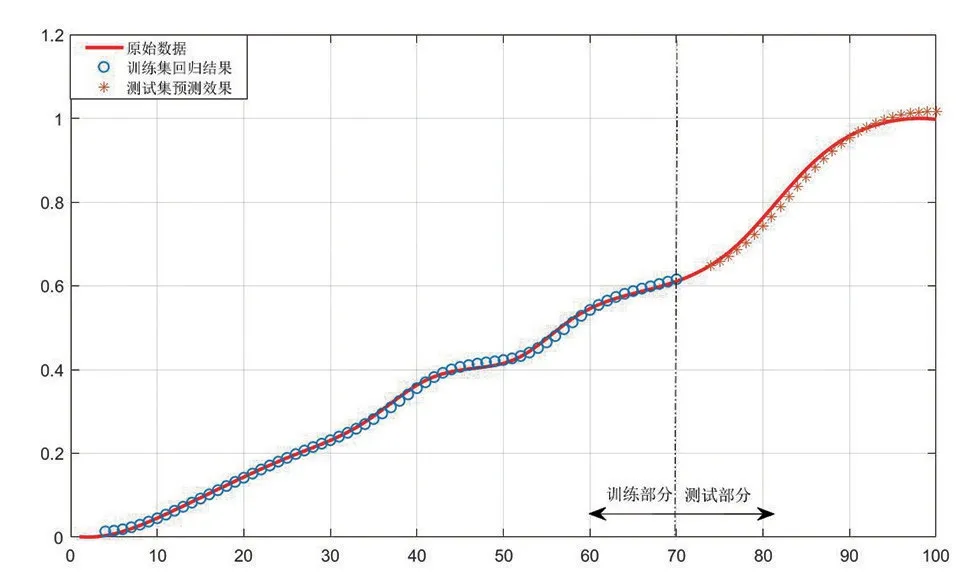
图5 分量RES的回归及预测结果

图2～5 分别为EMD 分解得到的3 个IMF 分量和剩余分量的回归及预测结果，其中实线代表的是原始数据，圆点代表模型的回归结果，星号代表模型的预测结果，可以看到，第1 个分量和第2 个分量的回归及预测结果比较理想，第3个分量及剩余分量的回归及预测结果非常理想。

2.6 还原区间及分量叠加

将得到的归一化后的模型的回归结果和预测结果还原区间，得到铁路客运量的各分量的回归结果和预测结果。还原区间的公式如下：

由于EMD 分解的各分量有如下关系，其中wi(t)为分解得到的各个平稳分量，bn(t)为余项。

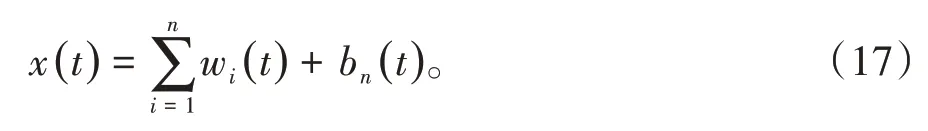
故将各分量同时刻的回归值叠加，就可以得到铁路客运量的回归值。叠加得到的铁路客运量的回归及预测结果如图6所示。

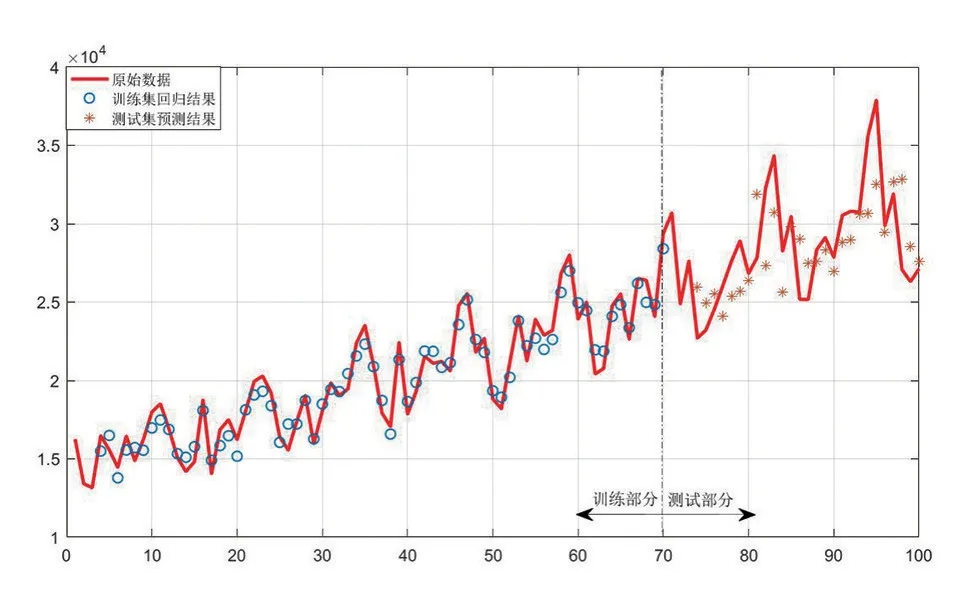
图6 铁路客运量的回归及预测结果

在图6 中可以看到，虽然个别值的误差较大，但总体上回归及预测效果不错。

2.7 误差分析

先使用建立的模型看其在训练集上的回归效果，计算出每个样本的相对误差以及整体的平均绝对百分误差，检验模型的回归情况，计算其MAPE 为0.54%，观察到这67 个样本Pe的大部分都小于10%，对于训练集，模型的回归效果达到了预期的精度。

再使用建立的模型看其在测试集上的预测效果，计算出每个样本的相对误差以及整体的平均绝对百分误差，检验模型的回归情况，结果如表4所示。

表4 测试集数据预测值及相对误差

计算其平均绝对百分误差（MAPE）为0.64%，观察到这27 个样本的绝对误差大部分都小于10%，对于测试集，模型的预测也效果达到了预期的精度。

3 结语

对使用EMD 和SVM 对铁路客运量进行了分析研究，由于铁路客运量数据不具有平稳性，所以先对铁路客运量进行了EMD 分解，分解得到3 个IMF 及一个余项；之后采用SVM 对每一个分量进行回归和预估分析，继而把同时间点的结果进行累加合计，便可完成整个模型的构建过程。可以看到，使用EMD和SVM 组合预测的方法虽然个别值有所差别，但总体预测效果理想，故对于非平稳的数据，可以使用EMD和SVM的组合预测的方式进行研究分析。