碰撞振动系统的牛顿迭代积分法与全局动力学
2021-04-06任一凡冯进钤沈晓娜
任一凡,冯进钤,沈晓娜
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
碰撞振动现象是生活中常见的一种现象,如列车行驶中车轮与铁轨之间的碰撞,机器运行中零部件之间的碰撞。这些现象有时会给人们的日常生活带来负面影响,所以,人们展开了对碰撞振动系统的研究,包括系统的周期运动、分岔和混沌。近年来,碰撞等非光滑因素的存在通常使得系统的轨线流出现跳跃和零行为等奇异性,使得在碰撞振动系统中出现了新的现象。对于这些新的现象,许多学者对此也做了很多的研究[1]。另一方面,由于不连续特性的存在,适用于光滑系统的数值积分方法不再直接有效,不连续时刻的数值定位成为碰撞振动系统数值研究中热点问题之一[2]。
对于非线性系统的全局分析方法分为解析方法和数值方法,而胞映射方法作为一种分析动力系统全局特性的有效数值方法,运行速度快,提高了工作效率[3]。胞映射方法由HUS在1980年首次提出,为研究动力系统的复杂运动提供了一种新思路[3-4]。该方法将系统离散化为胞,把感兴趣的胞空间分割,利用胞之间的转移关系研究原动力系统的动力学行为。随后,HSU又提出计算更加准确的广义胞映射方法和图胞映射方法[5]。为了提高胞映射的计算精度,JIANG等提出了胞参照点映射法[6]。随后,HONG等又将广义胞映射图论方法扩展到模糊动力系统问题的研究中[7]。贺群等引进图论的四元组,构建了瞬态胞分类方法,该方法在逼近动力系统的稳定流形和不稳定流形方面效果良好[8]。传统的胞映射方法主要针对光滑系统,在处理非光滑系统时必须建立合适的数值积分方法[9]。关于非光滑系统的胞映射方法,目前已有的研究较少。李爽等对边界胞进行了重新细分,提出了非光滑系统迭代图胞映射方法[10]。文献[11-13]基于图胞映射方法,提出了擦边流形的逼近算法,建立了适用于随机碰撞振动系统的自适应胞映射方法,并讨论了系统的全局结构,研究了噪声对全局结构的影响。
针对碰撞振动系统不连续的特性,建立高效的适用于碰撞振动系统的数值积分方法,难点在于解决非光滑系统的积分运算[14-16]。本文结合牛顿迭代法的思想,构建了适用于碰撞振动系统的数值积分方法。将该数值积分方法运用于Duffing型碰撞振动系统,验证了该数值方法的有效性与高效性;同时,将该数值积分方法融入胞映射算法中,研究了Duffing型碰撞振动系统的全局动力学。
1 碰撞振动系统的数值积分方法
考虑一般的二维碰撞振动系统,系统的动力学方程为
(1)

(2)
式中:x1=Δ;上标-、+分别表示碰撞前后的时刻;r表示碰撞恢复系数(0 在研究碰撞振动系统的动力学行为时,由于碰撞的存在,系统的轨线呈现不连续或不可微的情形,无法直接使用传统的数值积分方法。因此,建立数值方法准确定位碰撞时刻,是处理不连续性问题的关键之一。为了方便描述数值定位碰撞时刻,图1给出了牛顿迭代法示意图。 图 1 牛顿迭代法示意图Fig.1 Schematic diagram of Newton iteration method 将x1(tk+1)利用泰勒公式展开,得 (3) 根据约束条件,在式(3)中令x1(tk+1)=Δ,则 (4) 代入系统(1),解得 从而得到时间序列{tk},k=0,1,2,…的迭代格式 (5) 由式(5)可产生序列{tk},当|tk+1-tk|<ε时停止迭代,则t*≈tk,从而得出碰撞时刻t*的近似数值解。 假设RK积分步长为h,Δ表示碰撞面,T表示总积分时间。考虑一般的碰撞振动系统(1)、(2),采取经典的RK数值积分方法求解。数值解示意图如图2所示。 图 2 数值解示意图Fig.2 Schematic diagram of numerical solution 假设系统从tk时刻开始积分,在tk时刻的状态位置记为(x1(tk),x2(tk))T。对系统(1)进行RK数值积分,得到下一时刻的状态位置,判断这一位置系统(1)是否跨过碰撞面:若未跨过碰撞面,则继续进行下一步RK数值积分,直至跨越碰撞面;否则,利用迭代格式(5)和RK数值积分,数值定位碰撞时刻t*。然后,利用碰撞映射式(2)得到碰撞后状态,继续进行光滑系统(1)的数值积分。为了更加清晰准确地描述这一过程,给出具体的算法步骤如下: 步骤1:输入初始条件(tk,x1(tk)),k=0。 步骤2:从tk时刻开始积分,RK一步映射得到tk+1时刻的状态x1(tk+1)。 步骤3:判断这一时刻的状态是否跨过碰撞面:若跨过,则转步骤4;若没有跨过,转步骤5。 步骤5:若tk+1>T,转步骤6;否则,令(tk+1,x1(tk+1))→(tk,x1(tk)),转步骤2。 步骤6:输出结果。 考虑谐和激励下的Duffing型碰撞振动系统,系统的模型如下: (6) (7) 式中:a、c为常数;b为阻尼系数;x表示为广义位移;fcos(ωt)为谐和激励。 针对系统(6)分别作周期运动和混沌运动的情形,进一步验证上述数值积分方法的有效性。首先,固定部分系统参数,a=1.0,b=0.2,c=1.0,r=0.8,Δ=1.0,ω=1.0,取定初始值(x0,y0)T=(0.8,0)T,系统外激励周期T=2π/ω。 可知系统(6)在f=0.38时作周期运动,在f=0.42时作混沌运动[17]。利用上述数值积分方法,图3给出了系统(6)在谐和幅值f为0.38时的相图和时间历程图。可以看出,f=0.38时,系统作规则的周期运动。图4给出了f=0.42时的相图,可以看出,原来的周期运动消失,此时系统作混沌运动。 (a) 相图 (b) 时间历程图图 3 当f=0.38时,系统(6)的数值解Fig.3 The numerical solution of system (6) when f=0.38 图 4 f=0.42时系统(6)的相图Fig.4 Phase diagram of system (6) when f=0.42 可以得出,图3和4所得数值结果与文献[17]一致。此外,数值仿真过程中,迭代格式(5)中的精度取为1×10-8,最大迭代次数为3,说明该数值积分方法适用于碰撞振动系统的周期运动以及混沌运动的数值研究,并且具有较高的精度与稳定性。 为了更深入地分析非光滑因素在系统全局动力学中的影响,重点考虑谐和激励f对系统(6)全局结构的影响。固定部分参数a=1.0,b=0.2,c=1.0,r=0.8,Δ=1,ω=1.0;选取庞加莱截面 Π={(x,y,θ)∈R2×S:θ= ωtmod(2π)} 取状态空间的不同初始值(0.75,-0.3),(-0.75,0.3),(0,0.8),(0,-0.7)和(0.8,0)做庞加莱映射。去掉前100个瞬态周期点后,保留500个稳态周期点,得到多初值分岔图,如图5所示。 从图5可以看出:当f=0.38时,系统存在5个周期为1的共存吸引子;f增加到0.392,其中有3个周期解由倍周期分岔通往混沌,2个周期解的拓扑性质保持不变,此时,系统呈现出周期解与混沌解共存的现象; 当f∈[0.392,0.395]时,系统的混沌解逐渐消失,退化为3个周期为1的共存解;随着f逐渐增加到0.409,此时系统依旧是3个周期解共存。f继续增加至0.41,2个周期为1的周期解发生激变,直接进入混沌运动。 图 5 多初值分岔图Fig.5 Multi-initial bifurcation diagram 为了更深入地分析该系统的动力学演化,利用简单胞映射方法[17]探讨系统激发生前后的全局动力学行为。将感兴趣的区域 D={(x,y)|-1≤x≤1,-2≤y≤2} 划分成300×400个大小相同的格子,每个格子记为正规胞,区域D以外的区域记为陷胞,数值积分采用上述牛顿迭代积分法。 当f=0.38时,系统(6)的全局图如6(a)所示,其中Ai(i=1,2,3,4,5)表示与吸引子,Bi(i=1,2,3,4,5)分别表示与吸引子Ai对应的吸引域。此时系统存在5个吸引子,对应5个吸引域。为了更清晰地看出系统的运动状态,吸引子对应的相图如图6(b)所示,图6(b)由左上位置开始分别对应吸引子A4、A5、A1、A3、A2。可以看出,此时系统存在5个周期为1的运动,系统呈现出5种不同的周期运动,并呈现出一定的对称性,与图6(a)的全局结构图吻合。 (a) 全局结构图 (b) 相图图 6 当f=0.38时,系统(6)的数值结果Fig.6 The numerical solution of system (6) When f=0.38 随着谐和激励f逐渐增大到0.392,系统(6)的全局图如图7(a)所示。从图7(a)可以看出:吸引子A1、A2和A3的拓扑性质没有变化,而周期吸引子A4和A5消失,突变为混沌吸引子。此时,系统呈现出周期解与混沌解共存的现象。当f=0.394时,系统(6)的全局图如图7(b)所示。从图7(b)可知:吸引子A1和A3及其吸引域B1和B3一同消失,原先的混沌吸引子A4和A5退化成2个共存周期吸引子,系统呈现出3个周期吸引子共存的现象,系统经历了混沌解到周期解的激变。 继续增大f,在f=0.409时,系统依旧呈现出3个周期为1的吸引子共存的现象,见图7(c)。随着谐和激励f继续增加到0.41,此时系统的全局结构如图7(d)所示。从图7(d)可以看出:周期吸引子A2的拓扑性质没有变化,周期吸引子A4和A5突变为2个混沌吸引子,系统呈现出周期吸引子与混沌吸引子共存的现象,系统发生了周期解到混沌解的激变。 (a) f=0.392 (b) f=0.395 (c) f=0.409 (d) f=0.41图 7 系统(6)的全局结构图Fig.7 Global structure diagram of system (6) 本文构建了适用于碰撞振动系统的牛顿迭代积分法,并验证了该数值积分方法的有效性及高效性。同时,将该方法运用于胞映射算法中,研究了双边约束下Duffing型碰撞振动系统的全局结构。结果表明,改进后的数值积分方法适用于系统的周期运动和混沌运动的数值研究,并提高了计算速度。通过对系统全局动力学的研究发现,系统存在着丰富的多吸引子结构,如多周期吸引子、多混沌吸引子的共存现象。此外,谐和激励幅值的变化可以诱导系统发生多解激变现象,包括周期解直接进入混沌、混沌激变等。1.1 牛顿迭代法定位碰撞时刻

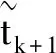
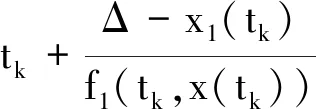
1.2 碰撞振动系统的数值积分方法
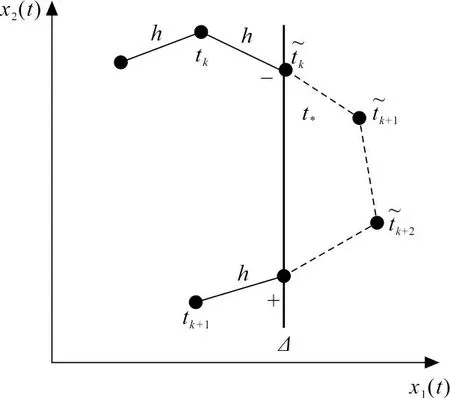

2 模型算例
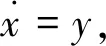
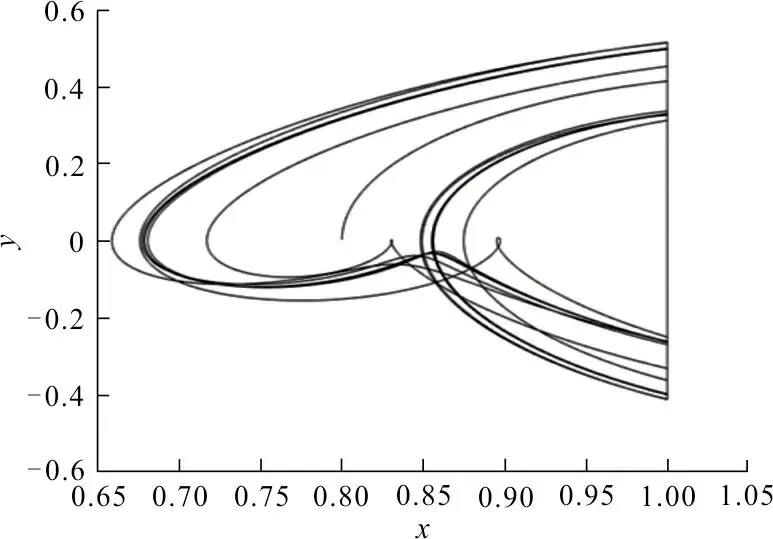


3 Duffing双边碰撞振动系统全局结构

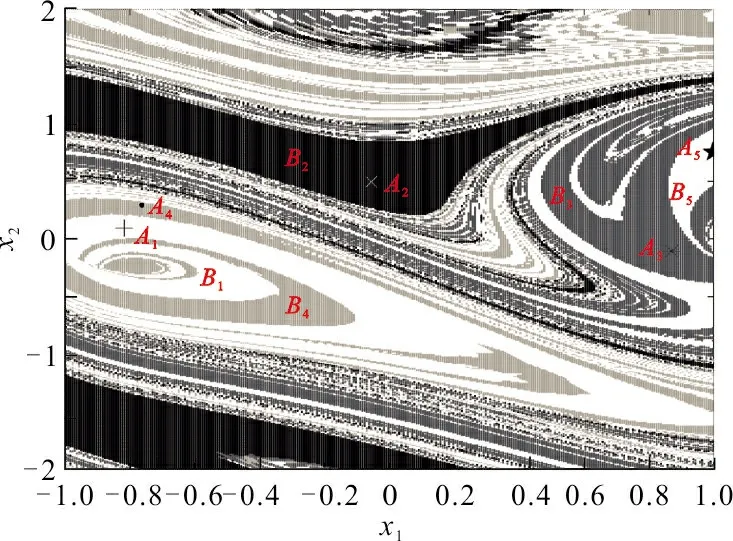
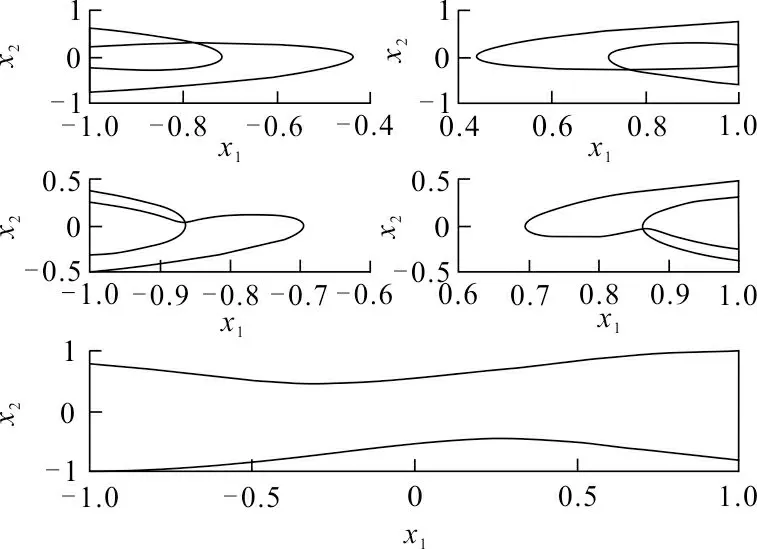



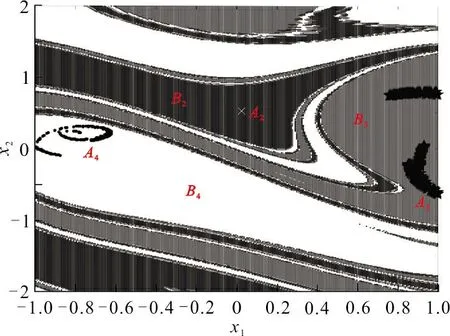
4 结 语
