自适应遗传算法在移动机器人路径规划中的应用

桑和成，宋栓军，邢旭朋，孟湲易,张周强,唐铭伟

(西安工程大学 机电工程学院，陕西 西安 710048)

0 引 言

移动路径规划是机器人研究领域不可或缺的一部分，也是机器人完成指定任务的重要保障和基础[1-3]。对保障机器人稳定工作，提高仓库运行效率起着至关重要的作用。

在解决路径规划问题方面，国内外学者做了大量的研究，遗传算法被证明是有效算法之一[4-6]。但是，基本遗传算法由于自身的局限性，不能解决路径规划中的问题。近些年一些学者对遗传算法进行了改进，取得了很好的效果。闫雪超等在种群产生时先判断、删除那些与障碍物相交的染色体；其次，提出新的变异算子，根据种群中适应度值大小调节变异节点。该方法使得转弯次数减少但增加了路径长度[7]。田欣利用先验知识，在保证遗传操作后所得的个体均为在可行路径的基础上提出新的自适应调整方式与之配合，同时于引入模拟退火算法Metropolis准则，对遗传操作产生的个体进行接收判定，寻优成功率和路径效果均得到了优化，但此方法不适合复杂地图环境[8]。陈志军等将遗传算法和模糊神经网络结合，求解最优目标函数并给出了三维路径规划评价指标,但整个算法过于繁杂[9]。宋宇等在种群初始化时，先结合RRT算法，再引入改进的插入算子创建邻居列表矩阵，得到的路径长度比基本遗传算法缩短70%，但算法收敛速度过慢[10]。雷永锋等基于正弦式遗传算法，通过改进交叉和变异策略，很好地解决了算法易早熟的现象,提高了算法收敛速度，但在路径寻优上还有待改进[11]。

机器人路径规划属于非确定性复杂问题。智能遗传算法是通过模拟自然界遗传操作的一种并行和全局搜索算法。因为能够在参数空间同时进行多点并行计算，所以更有可能搜索到全局最优，同时对其搜索空间没有连续的要求。但是，智能遗传算法在种群产生、适应度函数建模、搜索效率等方面还存在一定的缺陷[12]。特别是在复杂环境下，往往需要耗费大量时间才能规划出可行路径。针对这一问题，本文提出一种自适应遗传算法的机器人路径规划方法。该方法根据先验知识初始化种群缩短迭代次数，提出新的自适应策略，并根据适应度值大小自动调节交叉和变异概率，避免算法陷入局部最优；对于适应度函数，选取路径最短和平滑度双重约束，保证路径最短，且转折次数更少。

1 环境模型的建立及编码

将移动机器人工作环境表示成栅格地图的形式，如图1所示。图1中，自由栅格用白色表示，障碍物栅格用黑色表示，路径点的位置可以用直角坐标和栅格序号表示。采用二进制编码，栅格长度和宽度均为单位长度，分别标识栅格和坐标。栅格序号与其相对应的直角坐标一一对应，序号P(i,j)的栅格坐标表示为

(1)

式中: mod表示取余运算;[·]表示取整运算。

图 1 环境建模Fig.1 Environmental modeling

2 机器人路径规划

2.1 改进初始化种群方式

机器人在栅格法地图中，在未遇到障碍物和未超过地图边界时，默认可以向8个方向移动。这种方法虽能找到可行路径，但增加路径多变性，出现路径转弯次数过多、路径循环等现象，影响收算法敛速度，不利于机器人运行，故作如下改进：在机器人所在位置周围8个栅格中舍弃远离目标点的3个栅格，保留剩余5个方向进行初始化，具体流程如图2所示。

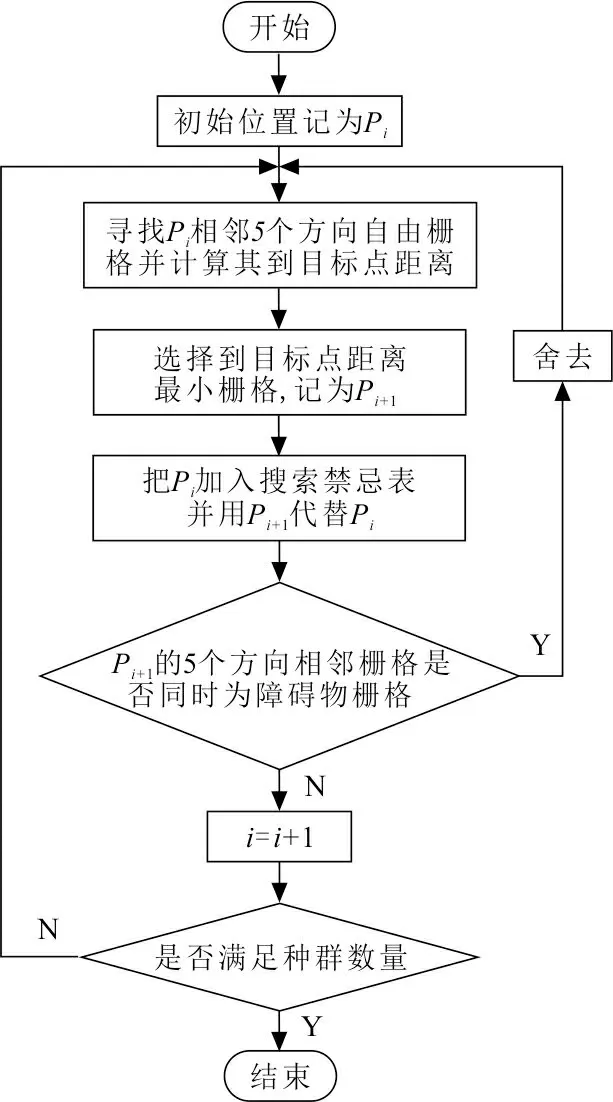
图 2 种群初始化流程Fig.2 Population initialization process

2.2 适应度函数的选择

机器人路径规划目的是寻找从起点到目标点最优路径，而适应度函数能有效评价每条路径的优劣程度。设计适应度函数首先应满足路径最短，其次应确保路径足够平滑。因此，本文中的适应度函数同时将路径最短和路径平滑度2个因素作为评价路径优劣的标准。

2.2.1 最短路径f1假设在一个路径中移动机器人个体从一个节点Pi(xi,yi)运动到下一个节点Px+i(xi+1,yi+1),则2节点间的距离di为

(2)

该个体总的移动距离L为

(3)

式中：n为该机器人运行总节点数。

适应度函数第1部分为

(4)

2.2.2 路径平滑度f2首先设定机器人每次移动一个栅格。根据相邻3个节点和相邻2个节点间的距离判断出此时机器人转动的角度。假设相邻3个节点的坐标分别为A(xi+1,yi+1)，B(xi,yi)，C(xi+2,yi+2)，路径段夹角可用余弦定理表示。

相邻2点间的距离为

(5)

相邻3点间的距离为

(6)

由余弦定理可以求出相邻3个点之间的夹角，根据角度的大小分别给予不同的惩罚值,即

(7)

式中:wk为惩罚函数系数;θ为相邻3点之间的角度。

适应度函数第2部分为

(8)

结合路径最短和路径平滑度,得出本文适应度函数为

fit=af1+bf2

(9)

式中:a和b分别表示最短路径和平滑度的权重系数。

2.3 交叉操作

本文采用单点交叉方式[13]，当且仅当2个交叉个体在交叉点的栅格序号相同时进行交叉操作。如果2个个体在交叉点相同的序号不止一个，则任选一处进行交叉。假设2个待交叉个体为父代A和母代B，选择交叉点序号为33，具体过程如图3所示。在交叉完成后通过比较父代和子代适应度值大小，决定其去留，即适应度值大的保留，反之舍去，这样可使算法总是朝着最优方向进化。

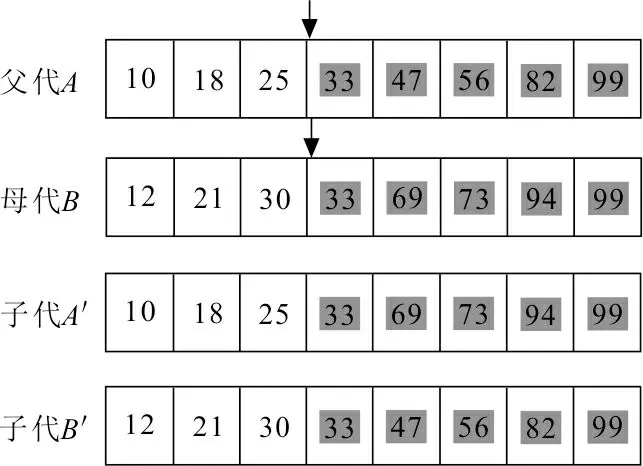
图 3 交叉示意图Fig.3 Cross diagram

2.4 变异操作

传统遗传算法变异操作是在变异位置随机突变，会导致变异前路径是可行的，变异后路径变为障碍路径，加大了不可行路径产生的概率。针对这一问题，本文提出新的变异策略。本文提出的变异过程及应对策略(见图4)如下：

图 4 变异策略Fig.4 Mutation strategy

1) 假设路径为[1 7 12 18 24 25](见图4),随机选择变异位置Bi为12号栅格。

2) 判断出Bi的右方13号、上方17号和右上方18号栅格均为自由栅格且未超出工作边界，此时，随机向这3个方向进行变异。

3) 向右方变异后的路径为[1 7 12 13 19 24 25]，向上方变异路径为[1 7 12 17 18 24 25],向右上方变异路径为[1 7 18 24 25]。此时，判断出变异后的3条路径均未经过障碍物,都是可行路径。若变异后的路径经过障碍物，则删除此条路径。

4) 分别计算出包括原路径的4条路径到目标点长度，得出[1 7 18 24 25]路径长度最短，用此路径替换原路径，完成变异操作。

2.5 自适应调整

遗传算法中交叉概率(Pc)和变异概率(Pm)对算法收敛性和路径求解质量起着至关重要的作用[14]，且传统遗传算法中(Pc)和(Pm)都固定不变，不利于种群的进化。Pc选择过大将会破坏群体的平衡性,导致适应度值大的个体被破坏；相反，选择过小将会延缓群体进化速度。同样，Pm选择太大群体进化方向多变,不利于优势个体保留；选择过小，不利于新个体的产生，算法易早熟陷入局部最优。所以，采用固定的Pc和Pm很难满足路径规划的要求。针对这一问题，本文对交叉和变异进行自适应调整改进[15-17]，调整为

(10)

(11)

式中:fav是每代群体的平均适应度值;f′是要交叉的2个个体中较小的适应度值，f是要变异个体的适应度值;设定k1、k2的区间为[0.6,1]。

由式(10)和(11)可以看出：新的自适应调整公式采用指数形式保证了交叉和变异概率呈现稳定的变化趋势，避免交叉和变异概率出现极度增大或减小的情况。进化初期群体良莠不齐，选择小的交叉和变异概率有利于群体中优良个体保留；相反，那些适应度值小的个体则被加快淘汰。在进化后期种群个体的适应度值无限接近,此时选择较大的交叉和变异概率加快新个体产生，避免算法陷入停滞状态，克服早熟[18-20]。

3 仿真分析

为了验证算法的有效性，选取2种不同环境对机器人路径规划进行仿真实验。环境1选取障碍物栅格数为19个，环境2选取障碍物栅格数为77个。设定对基本遗传算法参数如下：种群大小NP=100，最大进化代数G=100,交叉概率Pc=0.6 ，变异概率Pm=0.2。在本文算法中，路径最短权重系数a=4，路径平滑度权重系数b=3，种群大小及最大进化代数与基本遗传算法中的选择相同； 交叉概率Pc1=0.9，Pc2=0.6 ，变异概率Pm1=0.2，Pm2=0.1；在自适应交叉和变异概率中取k1=0.9，k2=0.8。对于环境1，2种算法仿真实验最优路径轨迹和收敛曲线如图5所示。

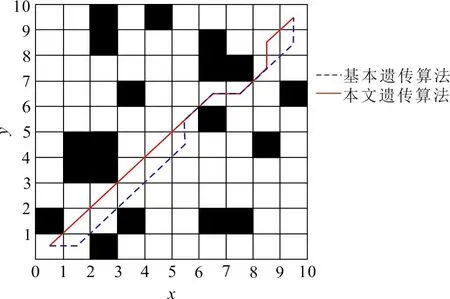
(a) 2种算法最优路径对比

(b) 最优路径进化曲线对比图 5 环境1最优路径及其进化曲线对比Fig.5 Comparison of the optimal path and its evolution curve in environment 1

从图5可以看出：在相对简单的地图环境中，基本遗传算法在第8代左右得到最优解，此时路径长度为14.486，路径中转折点数为6；而本文算法搜索到全局最优路径长度为13.314，路径转折点数为4。显然，相比基本遗传算法,本文算法路径长度缩短8.1%，转折次数更少，路径更加平滑。

环境2仿真实验最优路径和收敛曲线见图6。

从图6可以看出：在相对复杂的环境中更能体现本文算法的优越性。基本遗传算法在9代左右便陷入局部最优解，最终搜索结果为29.799，路径转折点数为15，没达到理想结果；而本文算法在第7代左右就趋于稳定，搜索到全局最优解为28.627，路径转折点个数为11。本文算法节约时间，路径更加平滑，同时也得到了机器人最优路径。

为验证本文算法的有效性，又选取了8种不同的机器人工作环境，即8种不同障碍物个数仿真实验。图7是障碍物个数为31和99的寻优结果。然后，对8种不同环境条件，各进行20次路径规划仿真实验，结果见表1。从表1可看出，对于本文的改进算法，随着障碍物个数不断增加，路径长度降低的比重逐渐增大，且路径中转折点个数相对基本遗传算法减少3～5个，算法迭代次数也优于基本遗传算法。

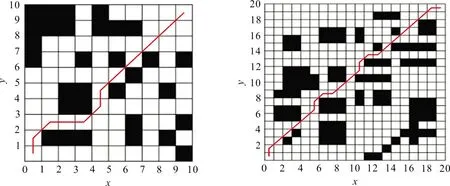
(a) 31个障碍物的路径寻优结果 (b) 99个障碍物的路径寻优结果图 7 不同障碍物个数下路径寻优结果Fig.7 Path optimization results in different number of obstacles

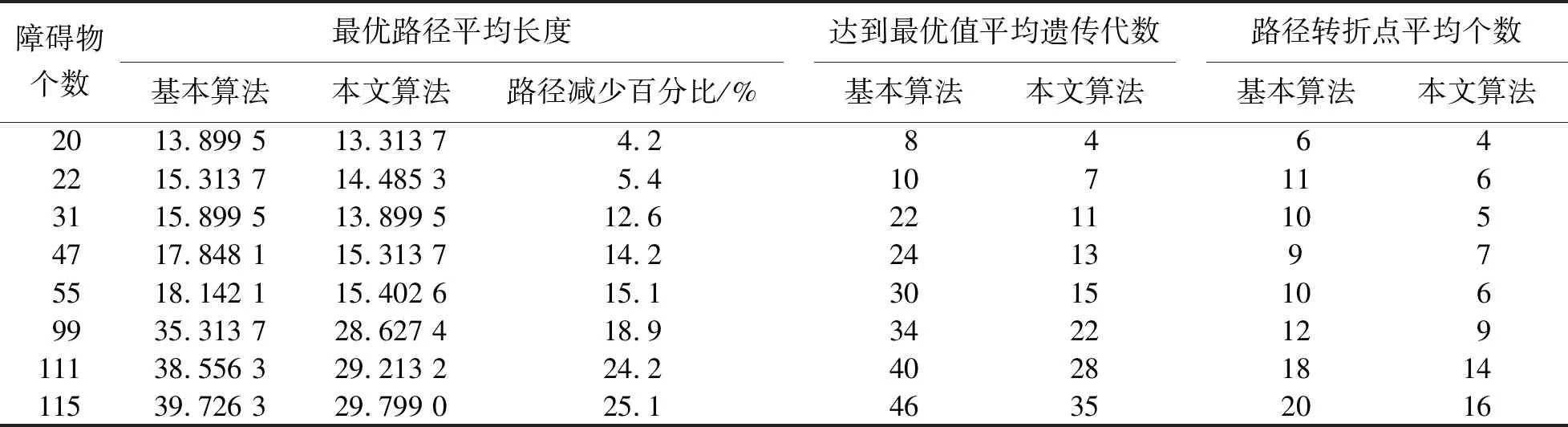
表 1 不同环境下路径规划仿真实验结果

4 结 论

1) 设计的自适应交叉和变异概率公式，避免了算法陷入局部最优，克服早熟的缺点。

2) 随着障碍物增多，在环境更加复杂的情况下，本文算法得到的最优路径更短、转折次数更少。仿真实验证明了算法的可行性。