基于时间序列分析的信号活动规律预测研究

何国金　吴荣军

摘  要：信号活动规律预测是有效利用大量随机电磁频谱监测数据和提取有用信号信息的重点，也是难点。如何从大容量、低成本的数据中提取电磁信号的价值信息，提高频谱监测数据利用的有效性是预测信号活动规律的核心重点。本文首先简单介绍了当前频谱监测数据的统计方法，然后采用时间序列分析方法预测信号在未来时刻信号强度，同时对采用的统計方法进行了分析和仿真。

关键词：电磁信号;信号强度;活动规律;时间序列分析

中图分类号：TP391.9      文献标识码：A 文章编号：2096-4706（2021）17-0078-04

Abstract： The prediction of signal activity law is the key and difficult point to effectively use a large number of random electromagnetic spectrum monitoring data and extract useful signal information. How to extract the value information of electromagnetic signal from high-capacity and low-cost data and improve the effectiveness of spectrum monitoring data is the core focus of predicting the law of signal activity. Firstly， this paper briefly introduces the statistical methods of the current spectrum monitoring data， then uses the time series analysis method to predict the signal intensity of the signal in future moment， and analyzes and simulates the statistical methods used.

Keywords： electromagnetic signal; signal intensity; activity law; time series analysis

0  引  言

随着社会无线电信息化的发展，各种短波通信、超短波通信、微波通信、广播、电视、雷达、导航等无线电业务的需求日益增长，研究特定信号的频谱特性、特征识别、活动规律，对提高频谱资源有效利用、异常信号捕捉等具有重要意义。

电磁频谱监测是对监测点周围的电磁信号辐射到监测点进入接收机的振幅/信号强度进行测量;目前主流的监测方法是频段数据扫描，利用该方法可以对特定频段内的信号快速搜索，根据一定门限对信号进行提取，形成监测信号列表。而对信号列表中的数据进行统计的方法比较笼统，比较频段占用度统计、信号持续时间统计、信号活动规律分析等，对数据的统计方法多采用指定门限或曲线门限切除，获得信号列表，后进行统计，都是瞬时统计，而且统计结果的准确性有待提高。

国内外对频谱监测数据分析多采用连续频段扫描、频谱占用度统计、信号解调与识别等统计分析，采用信号特征与样本库信号特征数据比对方法，这种数据比对方法必须在一定的条件下才能达到预期的效果，不是对所有的电磁环境都适用，并且对信号活动规律按照线性统计，识别准确率不高、统计结果价值低。

本文[1]根据目前国内外对信号规律统计方法存在的一些主要问题，提出了对频谱监测数据按时间序列[2]统计分析方法。它主要分为三个步骤：

首先，确定并分离季节成分，即将持续监测信号积累的数据剥离掉季节性成分。首先根据大容量的信号数据计算季节指数，然后将计算所得频谱监测数据的季节成分从无价值的时间序列数据中剥离掉，就是通过把每个时间段的序列观测值除以该阶段的季节指数，这样就可以消除频谱监测数据的季节性。

其次，建立预测数学模型并预测。对每个频谱监测数据消除了季节成分的时间序列建模，把每个阶段的数据带入求解。

最后，计算含有季节成分的最终预测值。将每个阶段求出的预测值与该时刻的季节指数相乘，这样就可以求出最终的预测值。

采用数理统计概率分析经典问题信号时间序列建模是很好的解决方法，利用时间序列的优点可以很简单地预测出指定信号下个时刻在监测点上的场强/电平，下面对所采用的算法进行研究和验证。

1  基于时间序列对信号活动规律预测建模

1.1  信号时间序列分析

信号时间序列分析（Signal Times Series Analysis）是相同指定信号在不同时刻上对应的场强/电平幅度值排列而成的数学序列，用t表示观察的时间，Y表示观察值，则Yi（i=1，2，…，n）为时间ti上的观察值。分为平稳序列和非平稳序列两大类。信号时间序列的成分分为四种，包括长期趋势（T）、季节变动（S）、周期波动（C）、不规则波动（I）。

信号时间序列分析就是把这个季节成分从时间序列中分离出来，同时把他们之间的相互联系用一定的数学模型或表达式加以表示再进行预测。

1.2  信号活动规律预测建模

信号时间序列建模的过程如下：

（1）通过社会调查、数据观测、样本抽样、统计分析等方式获取指定目标的时间序列变化数据。

（2）根据变化数据统计出其相关图，运用数学模型进行数据之间的关联性评估，解出自相关函数。通过统计图形能显示出数据变化趋势和变化周期，运用图形变化趋势可以找出跳点和拐点。如果跳点是正确的观测值，在数学建模时应把加权考虑进去，如果是异常情况，则需要把跳点通过修正数据为预期值。拐点是指信号时间序列数据中出现峰值或波谷值的点。如果存在拐点，则在数学建模的时候需要用不同的模型在不同时段平滑这个时间序列数据，使数据曲线图形平滑。

（3）依据时间序列数据建模，运用曲线平滑进行数据拟合，就是运用数学模型将所有频谱监测数据图形化结果进行平滑处理。对于小容量的频谱监测时间序列数据，可以运用曲线趋势拟合处理模型及置信区间所控制的误差来平滑拟合。对于大容量平稳型频谱监测时间序列数据，可以运用自回归滑动平均模型及其在特定情况的自回归模型、滑动平均模型或组合自回归滑动平均模型等来做平滑处理。

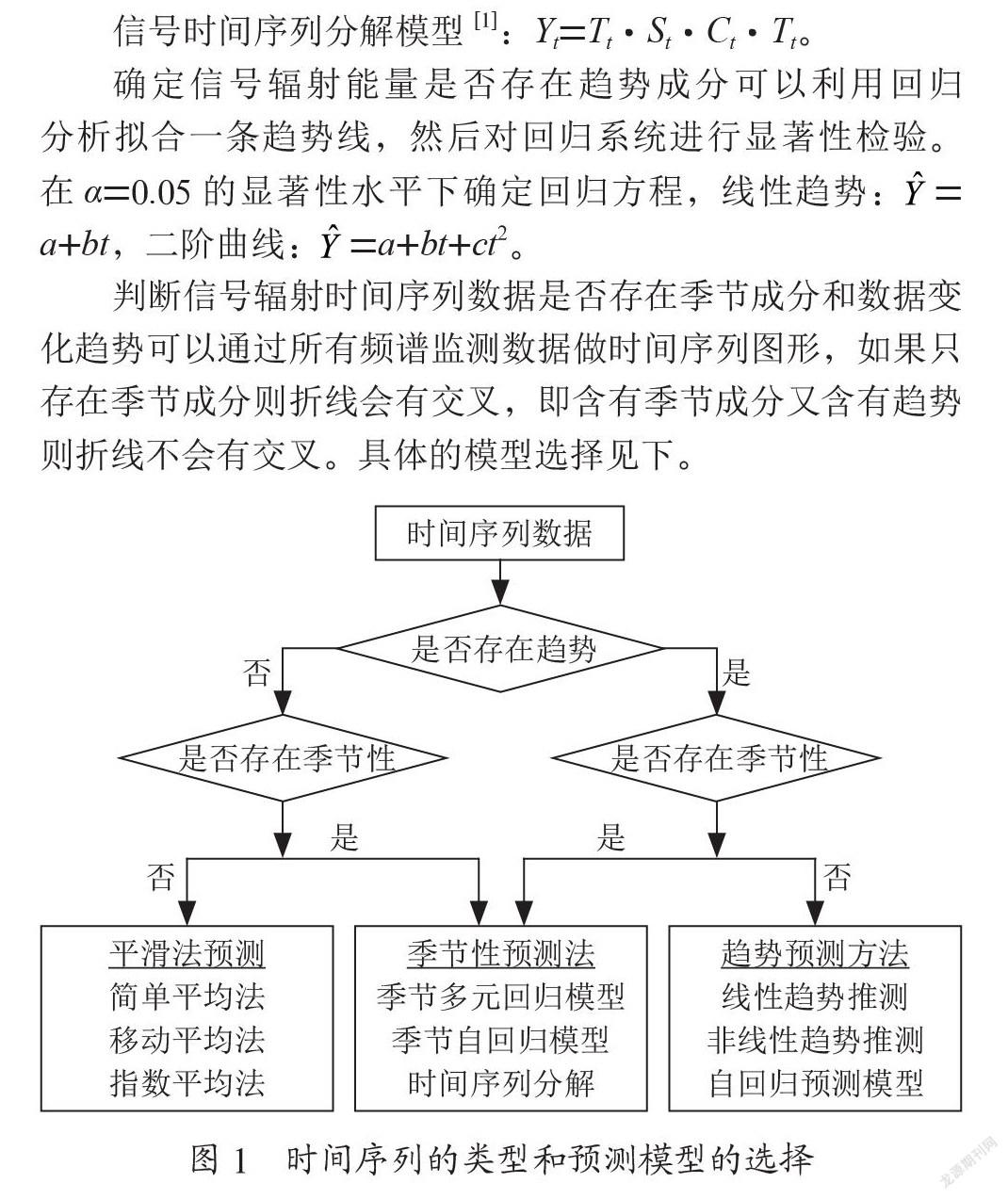
信号时间序列分解模型[1]：Yt=Tt·St·Ct·Tt。

確定信号辐射能量是否存在趋势成分可以利用回归分析拟合一条趋势线，然后对回归系统进行显著性检验。在α=0.05的显著性水平下确定回归方程，线性趋势：= a+bt，二阶曲线：=a+bt+ct2。

判断信号辐射时间序列数据是否存在季节成分和数据变化趋势可以通过所有频谱监测数据做时间序列图形，如果只存在季节成分则折线会有交叉，即含有季节成分又含有趋势则折线不会有交叉。具体的模型选择见下。

2  算法分析与验证

2.1  算法分析

下面对算法的具体执行过程进行描述，对上面建模得到的信号时间序列的预测方法采用时间序列分解法进行预测。具体过程如下：

（1）计算季节指数：首先，计算移动平均值。如果频谱监测数据序列是季节数据，则采用季节移动平均，如果是月份数据，则采用月份移动平均，并对所得的平均移动值进行中心化处理，即对所得的移动平均值在进行二项移动平均处理，这样得出的平均值为中心化移动平均值。其次。计算移动平均的季节（或月份）比率，将频谱监测时间序列的实际数据除上对应的中心化移动平均值。最后，进行季节（或月份）指数调整。就是将上面计算所得的季节（或月份）比率的平均值除以总平均值。

（2）分离季节成分：

季节成分分离后的序列：。

（3）建立预测模型并进行预测：第1步：根据分离季节性因素的序列确定线性趋势方程，得到各季度的预测值。第2步：将回归预测值乘以相应的季节指数，得到最后的预测值。

具体算法为：

（1）频域分析：对每个信号时间序列数据在一定的频域范围内应用图像学可看成不同变化周期振动值的重叠，频域分析就是对不同周期的随机性振动产生偏移量进行拟合[3]。当时间序列数据存在固定变量的周期分量时，通过数据生成的图形Q（ω）的峰值点分析这些振动偏移量的周期。在按季节记录的信号电平时间序列中，信号时间序列S（t）就可看成含有以季节为周期的确定分量，所以信号时间序列S（t）表示为周期图Q（ω）处有显著的峰值。

如果平稳随机序列的谱分布函数F（λ）具有谱密度f（λ）（功率谱），依据（2π）-1I（λ）这个情况去估计f（λ）的渐近无偏估计。如果求f（λ）的相合估计，这种情况用Q（ω）的适当平滑值去估计f（λ），最通常的方法为谱窗估计，即取?（λ）的估计，则谱分布F（λ）自身的相合估计可通过Q（ω）的积分直接获得。

（2）时域分析：要确定信号时间序列在不同时间段如何取值的数据之间结果关系。这种结构是用时间序列的自相关函数来描述的，称为时间序列的自协方差函数值[4]，即m=ES（t）是平稳随机序列的均值。通常采用一下参数，可给出m，γ（k），ρ（k）的估计，通过对时间序列的相关结构的了解，称为自相关分析。通过对它们之间的强、弱相合性及其渐近分布等问题的研究，是相关分析（时域分析）的主要问题。

（3）回归分析：假如信号时间序列S（t）等于确定性分）量φ（t）与随机性分量ω（t）的和，即S（t）=φ（t）+ω（t），通过样本值x（1），x（2），…，S（t）分析ω（t）的规律，统计时间序列分析中的回归分析问题。不同之处在于ω（t），一般不是独立同分布的，所以需要非常多的随机过程课程内容。假如φ（t）为有限个已知函数的未知线性组合的情况，可得公式中ω（t）是均值为零的平稳序列[5]，α1，α2，…，αs是未知参数是φ1（t），φ2（t），…，φs（t）已知的函数，称为线性回归模型。

可以得知回归分析的内容主要包括：

（1）当ω（t）的统计规律已知的情况，则需要对参数α1，α2，…，αs进行估计，预测x（T+1）的值。

（2）当ω（t）的统计规律未知的情况，不仅要估计以上的参数，还需要对ω（t）进行统计分析，比如谱分析、模型分析等等。

综上所述，面临一个非常重要的议题是：在相对寻常的情况下，需要证明α1，α2，…，αs的最小二乘估计，与它的线性最小方差无偏估计相同，是否具有相合性和渐近正态分布性质。最小二乘估计j（1≤j≤s）不涉及ω（t）的统计相关结构，是可以通过数据x（1），x（2），…，S（t）直接求出，最终还可算出（t）进行时间序列分析中的各种各样的统计分析，来替代对ω（t）的分析。从理论上已经证明，在通常的情况下，这样的替代具有相对合意的渐近性质。因为ω（t）真值不能直接获得，这些理论结论显然有着非常重要的实际作用。

2.2  实例验证

为验证算法的有效性、正确性，利用对某地域某特定信号进行电磁环境监测，采集不同季节不同时间监测数据，从中选择出民用广播电台频率（频段：80 MHz～108 MHz），监测频谱如图2所示。根据分离季节性因素的序列确定的线性趋势方程为：=30.606 7+0.559 2t，对其最终预测值、预测误差进行了计算，结果见表1。使用的频谱监测接收机是美国安捷伦科技有限公司的N9020a，监测软件是国产自研的频谱监测管理软件。

图3给出了信号电平的实际值和预测值及预测误差，从直观上验证了上述算法预测效果非常好。

预测2022年第1季度的信号电平，将t=21带入趋势方程，得 =30.606 7+0.559 2×21=42.35。

这个预测值是不含季节性因素的，如果要预测含有季节性因素的信号电平，则最终预测值为：42.35×0.792 2= 33.55。

3  结  论

综上所述，从数理统计的角度出发，利用信号时间序列分析的方法来研究预测电磁信号活动规律，对所采用的算法进行分析和验证，是对频谱监测数据中重点信号进行深度挖掘的有利试验，为大容量的频谱数据处理、分析提供了新的方法和手段。在发射信号频谱存在无序性、密集性特征的情况下，其分析计算结果可为预测重点信号活动规律，预测信号活动态势提供信息依据。尤其外军在台海、钓鱼岛方向活动时监测其频率及预测其外军活动规律，可为预测信号活动范围供判定依据，进而推测外军空中或海上平台离海峡分界线的距离。

参考文献：

[1] 贾俊平，何晓群，金勇进.统计学：第6版 [M].北京：中国人民大学出版社，2015.

[2] 聂淑媛.时间序列分析的早期发展 [D].西安：西北大学，2012

[3] 胡西娟，褚万霞.大数据时代下抽样方法问题探讨[J].经贸实践，2018，（13）

[4] 袁兴明，马鑫程，邢立鹏，等.SDCORS基准站运动趋势与高程方向周期性信号分析[J].矿山测量，2018，46（1）：99-104.

[5] MA P，MAHONEY M W，YU B. A statistical perspective on algorithmic leveraging [J].Journal of Machine Learning Research，2015，16（1）：861—911

作者简介：何国金（1981—），男，汉族，福建莆田人，中国人民大学统计学院高级研修班学员，高级工程师，本科，研究方向：大数据应用、电磁态势;吴荣军（1982—），男，汉族，安徽宿州人，讲师，博士，研究方向：信息与计算科学。