基于MATLAB的时间序列预测
2016-01-05钟敏芸
钟敏芸

摘要:在自然科学和社会科学各领域中,大量决策问题离不开预测,预测是决策的基础。时间序列是利用现有的历史数据构造模型,进而预测未来。因此,该文首先介绍了定量化的时间序列预测目前采用的一种方法与预测模型,然后在分析时间序列预测相关概念的基础上,研究了其实现方法。
关键词:预测;时间序列分析;模型;精度
中图分类号:TP393 文献标识码:A 文章编号:1009-3044(2015)29-0206-03
The Prediction of Time Series Based on Matlab
ZHONG Min-yun
(GanzhouTechnician Institute, Ganzhou 341000,China)
Abstract:In each field of natural science and social science,a great deal of decision problems can not get away from the prediction which is the foundation of the decision. Time series is making use of the existing history data to establish a model to predict the future.Therefore,in the paper,firstly, introduces the current ways and models that the quantitative time series prediction adopt and the character and summarizes the aspects of the current ways and model.Then basied on the analyzing the related concepts of the prediction of time series,studied the basic ideas and implementary methods of these algorithms and models.
Key words: the prediction; the time series analysis;model; precision
预测是指对事物的演化预先做出的科学推测。随着科学技术的发展和社会的进步,人类对预测未来的要求越来越高。预测学这门古老而又崭新的交叉学科,充分运用现代科学技术所提供的理论、方法、手段来研究人类社会、政治、经济、军事以及科学技术等各种事物的发展趋势。预测研究过程中对近期影响、中期变化和远景轮廓的描述为人们制定近期、中期、长期规划以及进行科学决策提供依据。
1时间序列分析
时间序列分析是根据系统观测得到的时间序列数据,通过曲线拟合和参数估计来建立数学模型的理论和方法。其具有两大特点:(1)事物发展具有持续性,时间序列分析法是根据序列过去的变化趋势预测未来发展变化的,必须是从过去到现在并发展到未来,基本上不脱离其轨迹,能够延续下去,因此其前提是假定事物发展具有持续性。(2)时间序列数据存在着趋势,时间序列数据由于受到各种因素的影响,其变动趋势不可能完全一致[1]。一般来说,时间序列数据的趋势主要有以下几个方面:(水平变动趋势,时间序列的各个数据呈现出围绕某个稳定值(平均值)的变动形态。(长期变动趋势,在一定时期内呈现出持续上升或下降的变动形态。(季节变动趋势,以年为周期,按月、季给出的时间数列,呈现出随季节变化且每年反复有规则波动的变动形态。④不规则变动趋势,时间序列所呈现的变化趋势向没有一定规则,忽升忽降的变动形态。
而时间序列分析的作用,概括起来,主要有以下几个方面:
①对理论性模型与数据进行适度检验,以讨论模型是否能正确地表示所观测的客观现象。
②描述系统所处的状态及其结构性,从而达到认识和解释系统的目的。
③描述系统的运行规律性。
④预测并控制系统的未来行为,通过调整时间序列模型的输入变量,使系统发展过程保持在目标值上,从而达到预测和利用系统的目的。
2 Matlab的介绍
MATLAB 产品家族是美国 MathWorks公司开发的用于概念设计,算法开发,建模仿真的集成环境。MATLAB是建立在向量、数组和矩阵基础上的一种分析和仿真工具软件包,包含各种能够进行常规运算的“工具箱”,如常用的矩阵代数运算、数组运算等;同时还提供了编程计算的编程特性,通过编程可以解决一些复杂的工程问题;也可绘制二维、三维图形,输出结果可视化。它是一个高性能的科技计算软件,广泛应用于数学计算、算法开发、数学建模、数据分析处理及可视化、科学和工程绘图等。
3 时间序列预测模型及实例应用
时间序列预测法主要用于分析影响事物的主要因素比较困难或相关变量资料难以得到的情况,预测时先要进行时间序列的模式分析[2]。时间序列预测法包含指数平滑法、自回归移动平均模型等多种方法与模型,下面详细介绍自回归移动平均模型时间序列预测方法。
3.1基本数据
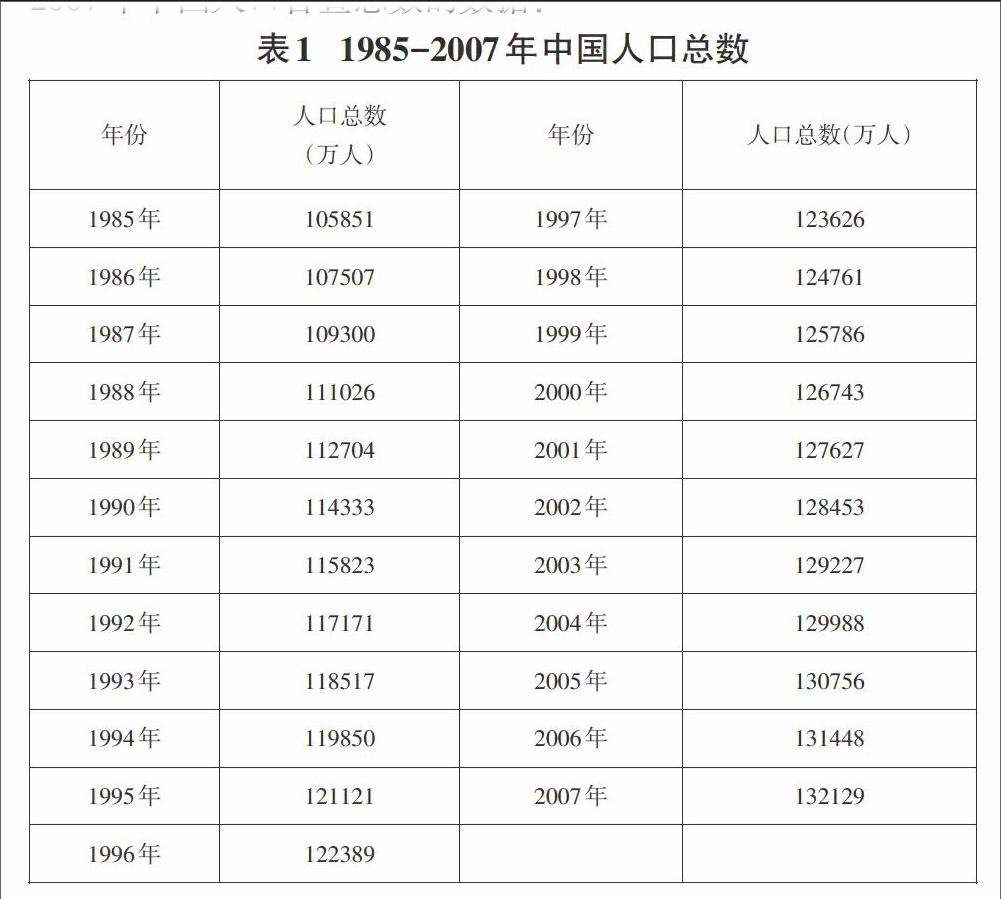
①预测采用来自《2008年中国统计年鉴》中我国1985年-2007年中国人口普查总数的数据:
②对模拟值处理的m文件代码:
x = [1985 1986 1987 1988 1989 ... 2007];
y = [105851 107507 109300 111026 ... 131448 132129];
plot(x,y),hold on;plot(x,y,'*');title('中国人口普查总数', 'FontSize', 10);
xlabel('年份', 'FontSize', 10); ylabel('人口总数(万)', 'FontSize', 10);
grid on
③结果如图1所示:
本文采用的数据取值为前15个原始数据对剩下的8个原始数据进行预测,最后预测的结果与现有的最后8个原始数据进行比较,算得误差,检测模型拟合效果及预测精度。
3.2 自回归移动平均模型(ARMA)
ARMA序列的数学模型是有限参数线形模型。
1)只要确定出有限个参数的值,模型也就完全确定。用它们来对数据进行拟合,考察数据内在的统计特征以及作最佳预报时数学上的分析处理都比较方便。
2)AR(p)、MA(q)和ARMA(p,q)序列的谱密度都是有理谱密度,而连续谱密度可以用有理谱密度来逼近,并能达到理想的近似程度,所以利用AR(p)、MA(q)或ARMA(p,q)模型作为基本的时间序列模型。
①matlab代码
function armademo
Parameter:
nseq = [105851 107507 109300 ...132129];nseq = nseq';nseqdata = iddata(nseq(1:15));
m = armax(nseqdata,[3,3]); yfilter = predict(m, nseq(16:23));
x = [2000 2001 2002 2003 2004 2005 2006 2007]; y = nseq(16:23);
yar = yfilter; plot(x,y, '-b*',x,yar, '--rs','LineWidth',2, 'MarkerEdgeColor','k','MarkerFaceColor','g', 'MarkerSize',2);
disp(sprintf('The result is: %f,\n', yar));
mse = MSE(nseq(16:23), yar); avmae = mae(nseq(16:23), yar);
rerr = releaterror(nseq(16:23), yar);
disp( sprintf('The mean square error is: %f', mse ));
disp( sprintf('The avarage real error is: %f', avmae ));
disp( sprintf('平均相对误差 is %f', rerr));
title('中国人口普查总数ARMA模型预测', 'FontSize', 10);
xlabel('年份', 'FontSize', 10); ylabel('人口总数(万)', 'FontSize', 10);
grid; legend('actual data','arma'); grid on
②截图
考虑到多个因素,综合得出的ARMA(p,q)模型的阶数p和移动平均项数q的取值分别为3和3。
根据ARMA(3,3)模型的计算公式[3],预测结果和实际值的拟合情况见图2:
③误差分析
其平均相对误差MRE= 0.000174 平均绝对误差MAE=22.668096 均方差MSE=783.483517
通过以上分析可以得到:自回归移动平均模型(ARMA)的预测效果还是比较理想的,说明自回归模型在我国人口普查总数的预测中切实可行。
对于时间序列的预测仍将是未来几年的研究热点,由于技术的原因以及作者自身学识的浅薄,本文的研究尚有许多不足之处,现简单总结如下,以为今后的工作、学习和研究提供思路和借鉴:
时间序列预测方法及模型是近年来的热点研究领域,涉及诸多学科,应用领域非常广泛。加强其理论基础知识的学习,增加自身知识的储备,这将是作者今后必须要不断加强的方面。
本文的研究仅限于一元线性时间序列分析方法,而目前多元时间序列分析方法非线性时间序列分析方法的应用领域更为广泛,考虑将本文所研究的内容拓展至多元。
由于作者水平有限,文中不妥和错误之处在所难免,恳请各位专家、教授批评指正,不吝赐教。
参考文献:
[1] 吴喜.时间序列分析与综合[M].湖北:武汉大学出版社,2004.
[2] 陈仲生.基于Matlab7.0的统计信息处理[M].湖南:湖南科学技术出版社,2005.
[3] 袁以美,叶合欣.MATLAB在经济评价中的应用[J].水利科技与经济,2004,10(3):52-57.
[4] 李南南,吴清,曹辉林.MATLAB 7简明教程[M].北京:清华大学出版社,2006.
