基于线性地物要素的综合化简算法设计与实现
2021-04-05陈锋

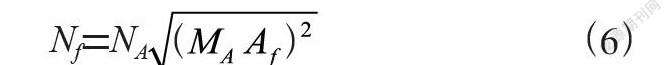

摘 要:我国河流水系分布众多,为满足生产需要,在众多水系中提取主要的河流至关重要。文章采用开方根法和Douglas-peucker法,利用C#语言实现化简程序,同时与GIS软件化简结果进行对比分析。研究表明,利用算法程序化简的河流条数与GIS的相同为52条,但是河流节点数为965个,比GIS的化简结果少了40个节点,且化简水系图更加平滑和美观,自动化程度更高,可以用于从大量的河流中提取主要的河流。
关键词:线状地物要素;Douglas-peucker法;开方根法;自动综合
中图分类号:TP311 文献标识码:A 文章编号:2096-4706(2021)17-0017-05
Abstract: There are many river systems in China, in order to meet the needs of production, it is very important to extract the main rivers from many river systems. In this paper, the square root method and Douglas-peucker method are used to realize the simplification program in C# language, meanwhile, the simplification results of it are compared with those of GIS software. The research shows that the number of rivers simplified by the algorithm program is the same as that of GIS, which is 52, but the number of river nodes is 965, which is 40 nodes less than the simplification result of GIS, and the simplified river system map is smoother and more beautiful, with a higher degree of automation. It can be used to extract the main rivers from a large number of rivers.
Keywords: linear ground object element; Douglas-peucker method; square root method; automatic synthesis
0 引 言
計算机技术的快速发展,使得地图制图综合技术由传统的方法向数字化和智能化的方向转变。测绘的成果主要表现为地表形态的地图,因此对地球形态的认识以及对地图制作方法的改进是测绘学发展的重要标志。当前人类社会已经进入信息化时代,制图技术有了跨越式的发展。由传统的地图生产方式向数字化、自动化和智能化的方向转变,在这个过程中,地图制图综合作为地理信息系统和地图生产过程中不可回避的问题,变得尤为重要。从整个地图科学方面考虑,地图综合是人类认识客观存在的具体表现,是人类进行空间信息处理的核心概念。
在数字信息系统中,线性特征通常由采样得到的离散点来描述。得到的采样点个数越密集,对原始特征的描述能力就越强,所呈现的原始特征就越真实。随着数据量的不断增加,对数据的管理和分析变得愈发困难。因此,有必要对线性特征元素的数据进行压缩。这个过程也称为线性特征简化,即用尽可能少的采样点来描述原始特征,保证原始特征的真实形态特征能够在允许的误差范围内再现。从信息理论的角度来看,线性特征元素集成技术本质上是一个问题的信息压缩,从组合曲线点集中提取序列的一个子集,将这个子集作为新的信息来源,在规定的范围内,精确子集可以真实反映原始收集尽可能多的内容,但尽量减少数量。本文以长江水系分布图为研究对象,利用GIS对长江水系图配准、矢量化。提出了基于(C#语言)Douglas-peucker算法和开方根规律法编写线性要素化简程序,实现线性地物要素的自动综合化简,并对化简结果进行对比分析。
1 道格拉斯算法与开方根算法
1.1 Douglas-peucker算法
道格拉斯算法是一种将曲线近似为一系列的点并减少点数量的算法。它具有平移和旋转不变性的优点,在给定曲线和阈值后采样结果是恒定的。公式为:
道格拉斯算法的优缺点:
优点是经过平移和旋转后不改变原有的特性,在给出具体的阈值和数据后,抽样结果是一个定值。缺点是当曲线拥有非常重要的地理意义且情况复杂时,Douglas-peucker算法的缺陷便显露出来,大致情况为,在某一化简尺度下经过化简的曲线会出现自相交或者相邻的曲线之间出现相交的情况。因此,空间数据拓扑关系的正确与否至关重要,一旦出现错误就会导致无法正确地在地图上显示地理信息,更重要的问题是会导致评估和决策错误。为了保证化简结果的准确性,必须要做到前后拓扑关系正确以及解决化简过程中出现相交与自相交的问题,并且在化简之后也可能会出现某些重要特征点的缺失。
1.2 开方根算法
开方根规律法是提出一种地图概括的数量处置方法,用于解决资料地图与新编地图由于比例尺的变换而产生的地物数量简化问题。公式为:
Nf=NA (6)
其中,Af是新编地图的比列尺分母,MA是原始地图的比列尺分母,NA是原始地图的地物数,Nf是新编地图的地物数。
开方根算法的优缺点:
开方根规律法公式直观地显示了制图综合时从重要到一般的选取指标,是一个有序的选取等级系统。开方根公式是线性方程,在地图比例尺固定不变的条件下,地物要素的选取比例保持一致。开方根公式的缺点是没有考虑到地理差异,特别是未将制图地物分布的密度变化考虑在内。
1.3 数据处理
将一幅满足条件的长江水系简图通过ArcGIS10.2软件进行影像配准,已知长江水系简图中七个点的地理坐标值,但是长江水系简图中x轴和y轴的比例是不协调的,这时候我们可以考虑让x轴乘以一个常系数(这里是10 000),然后进行坐标匹配。完成坐标匹配之后,点击添加控制点,此时即可完成长江水系简图校正。利用GIS的编辑工具将校正后的水系图进行矢量化,矢量化完成以后,需要将河流的地理坐标系向直角坐标系转化,然后坐标系需要选择投影坐标系中的WGS 1984 world Mercator坐标系。完成坐标系转换后,需要将要素折点转点,如图1所示。
利用GIS工具中的数据管理工具添加XY坐标,将属性数据导出为TXT文本格式,将导出的数据整理为Excel表格,并将一些不需要的数据删除后得到所有节点的点名和坐标数据。再将河流经过坐标投影后的线图层中的属性数据表导出、整理为Excel表格得到所有的线名,河流长度数据。分别如表1(河流局部数据)和表2(河流局部数据)所示。
2 界面设计与核心代码
2.1 界面设计功能实现
利用Visual studio 2013编程软件,采用面向对象编程技术来完成线性要素化简程序界面设计。根据程序功能的需要,添加相应的组件(如菜单栏控件、工具栏控件、桌面控件(tabControl1)、openFileDialog1控件、saveFileDialog1控件等组件)来实现打开、保存、开方根计算、道格拉斯计算、数据显示、图形可视化等功能。程序功能界面如图2所示。
2.2 核心代码
化简模块主要分为两项,首先是通过开方根规律法对河流数据进行数量化简,再用道格拉斯算法对已经进行河流数量化简的数据进行节点化简和压缩。下面给出了开方根算法和道格拉斯算法的核心代码:
(1)开方根算法核心代码为:
double L,C,K;//定义三个双精度变量。
int A,B;
C=math.sqrt(A/B);//利用开方根函数计算开方根。
K=C*L;
(2)首先要声明线段起点和线段终点,新建一个待检查的节点堆栈和压缩结果的堆栈;定义一个读取阈值,再设置一个初始起点和初始终点。将初始起点压入结果堆栈,初始终点压入待检查的节点堆栈中。用while循环来执行当待检查的节点堆栈元素,当元素不为空时执行循环;若元素为空,则说明压缩算法执行完毕。While循环中的if判断起点和终点之间是否还有其他节点,如果有则执行下面的语句。道格拉斯算法的核心代码为:
Pnt P0=new Pnt ();//声明线段起点。
Pnt P1=new Pnt();//声明线段终点。
Stack
Stack
Int intYuZhi=Convert.ToInt16(toolStripComboBox1.Text);//读取阈值。
Po=oriPnt[0];//设置初始起点。
P1=oriPnt[intoriPntNum-1];//设置初始终点。
rePnt.Push(P0);//初始起点压入结果堆栈。
proPnt.Push(P1);//初始终点压入待检查的节点堆栈。
while(proPnt.Count !=0)//当待检查的节点堆栈元素不为空时,执行循环;若元素为空,则说明压缩算法执行完毕。
{if(P0.ID !=P1.ID-1)
//设置一个线段距离最大的节点,并初始化它到线段的距离最小。
Pnt maxPnt=new Pnt();maxPnt.Dis=0;
//循环线段起点和终点之间的所有其他节点,若距离大于maxPnt则代替它。
for(int j=P0.ID+1;j<=P1.ID-1;j++)
{Pnt tempPnt=new Pnt();
tempPnt=oriPnt[j];
tempPnt.Dis=Distanct(P0,P1,tempPnt);//调用一个自定义函数Distanct,返回值为点到线段的距离。
if(tempPnt.Dis>maxPnt.Dis)
{maxPnt=tempPnt;}
}
//找出距離线段距离最远的节点以后,比较其距离和阈值的大小。
//若大于阈值,则将节点压入到待检查的节点堆栈,并将该节点设置为线段的终点。
If(maxPnt.Dis>intYuZhi)
{P1=maxPnt;proPnt.Push(maxPnt);
}//若小于阈值,则将终点设置为线段起点,并压入到结果堆栈中,并将待检查堆栈顶部的节点设置为线段终点。
Else //判断起点和终点之间是否还有其他节点,如果没有则执行:
{P0=P1;rePnt.Push(P0);
proPnt.Pop();
if(proPnt.count !=0){P1=proPnt.Peek();}
}}
While(rePnt.count !=0)//置换堆栈中节点的顺序。
{proPnt.Push(rePnt.Pop());}
}
3 结果分析
3.1 GIS软件下化简结果
将矢量化后的长江水系简图数据文件导入软件,再将已投影的矢量化线状图层拖到窗体中。并对矢量化的线状要素图层进行要素折点转点,通过开方根算法将原始比例尺为1:1 000 000的长江水系简图化简为比例尺为1:4 000 000的水系图,将利用开方根算法化简后的河流按照河流长度的大小排序。并将小于阈值205 215.772 6 km的河流删除,此时通过人机交互的方式对河流的数量进行化简,化简后的新编地形图上的河流数量为52条。其次使用ArcGIS的制图工具中的制图综合,利用Douglas-peucker算法进行河流节点的化简与压缩,对河流线状要素进行综合化简的效果从总体上来说还是非常实用和美观的。结果图如图3所示。
3.2 算法化简结果
打开线性要素综合化简程序所在的文件夹。打开文件夹以后,找到该程序并点击运行按钮即可。此时就会生成线性要素综合化简的界面,点击打开按钮,同时把河流ID和河流长度文档以及河流坐标文档导入界面之中。然后点击开方根算法按钮,对河流要素的数量进行化简,然而,采用的阈值是河流的长度小于205 215.772 6 km的长度,大于这个阈值的河流予以保留。
将开方根算法化简后的河流数量保存,并使用道格拉斯算法按钮对化简后的河流数量进行河流节点化简和节点压缩,将结果保存。化简后的河流线状要素图形如图4所示。
3.3 化简结果对比
在ArcGIS10.2软件支持下并不能很好地按一定的阈值对河流的数量化简,只能通过操作人员的手动操作来删除不需要的河流线性要素。这一点是比较麻烦的,不但给实际操作人员带来非常大的工作量,而且还会产生很大的误差。这就要求工作人员时刻仔细认真,以避免不必要的麻烦和相应的后续工作。
在使用线性地物要素综合化简程序的过程中主要用到两个线性要素化简算法,分别是开方根算法和道格拉斯算法。首先将相关的河流数据导入化简界面中,利用开方根算法对河流数量进行化简,再利用道格拉斯算法对化简的结果进行河流节点化简和压缩。此过程中可以利用开方根算法对大量的河流线状要素进行数量化简,并利用道格拉斯算法对化简的结果进行节点化简和压缩。此过程可以节省大量的时间,提高工作人员的工作效率,对线状要素的综合化简效果更好。可以为满足实际需求而做出相应的改变。同时还减少了经费的支出,节省了大量的人力财力。
将化简前的长江水系简图数据、ArcGIS10.2软件支持下的线性要素化简可视化结果和线性地物要素综合化简程序的化简结果进行整理,并将其河流的节点数和河流条数统计在同一张表中进行比较分析,如表3所示。
通过对化简后的图形和表格数据进行对比分析,得出以下结论:
(1)由上表可知,利用算法程序化简与利用GIS软件化簡的河流数量相同,都为52条,其中算法程序化简河流的节点数量要比GIS软件化简数量少,且图形更平滑。
(2)在图形上,算法程序化简的结果比GIS化简的结果更优化、平滑、美观。
(3)在自动化方面,算法程序化简比GIS化简更优化,其人工编辑的部分少,自动化程度更高。
4 结 论
由于计算机技术发展迅速,信息化的程度越来越高,在线性要素制图方面可以实现综合的化简算法向自动化方向发展。将相关的算法与人工智能相结合,优化算法结构,使其更好地为工作人员服务。
然而,传统的道格拉斯算法在计算过程中通常没有考虑到记录的中间距离最大的节点,导致循环时间和递归嵌套层次过深,影响了程序的运行效率。本文提出一种基于堆栈数据结构的分段道格拉斯算法。从曲线的一端开始,取起始点和终止点作为改进道格拉斯算法的工作范围。然后,确定最远点的距离是否大于规定限差,从而完成线性要素的化简。本文的Douglas-peucker算法,通常使用堆栈记录中间结果,得到最终结果。为了保证曲线的极值点不被删除,将曲线在弯曲极值点处分成两段,弯曲极值点由中间点与相邻两个顶点的夹角来测量。
根据结果对比可以看出,虽然结果相差不大,但在相同的阈值下,线性地物要素综合化简算法程序的自动程度更高,结果更优化。
参考文献:
[1] 齐清文,姜莉莉.面向地理特征的制图综合指标体系和知识法则的建立与应用研究 [J].地理科学进展,2001(S1):1-13.
[2] 王留召,梁洪有,米振通.地图自动综合的现状及发展方向 [J].中州煤炭,2001(6):15-16.
[3] 应申,李霖.制图综合的知识表示 [J].测绘信息工程,2003(6):26-28.
[4] 裵廷睿.主成分分析与系统聚类法在评估经济效益中的应用 [J].湘潭大学自然科学学报,1995(2):30-33.
[5] 陈波.道路网自动制图综合的研究和实践 [D].郑州:解放军信息工程大学,2006.
[6]毛赞猷,朱良,周占鳌,等.新编地图学教程:第2版 [M].北京:高等教育出版社,2008.
[7] 初宏晟,刘颖,宋国大.保持图形特征的线状要素的化简方法 [C]//2008年(第十届)中国科协年会.郑州:中国科学技术协会,2008:562-565.
[8] 汪琦,陈飞翔,彭俊杰.适用于移动平台的快速生成地形剖面线方法 [J].地球信息科学学报,2015,17(7):830-836.
[9] 张利君.土地利用总体规划制图综合方法研究 [D].上海:华东师范大学,2011.
[10] 李巧,董箭.道格拉斯-普克改进算法及其在海图岸线制图综合中的应用 [C]//第十届东北三省测绘学术与信息交流会.漠河:中国测绘学会,2009:378-380.
作者简介:陈锋(1994—),男,汉族,安徽六安人,硕士研究生在读,研究方向:矿山开采沉陷监测。
