基于ARIMA模型的福建碳排放权市场价格分析

李若山

（南京林业大学经济管理学院，南京 210037）

1 文献综述

《京都议定书》的出台与生效，赋予碳排放权（以二氧化碳排放权为主）以商品属性，因此国际范围的碳排放权交易机制正逐渐形成。作为最大的发展中国家以及最大的碳排放国，中国正在碳排放交易这一领域做出不懈努力：目前中国在北京、上海、天津、重庆、广东、湖北、深圳以及福建共8处设立了碳排放权交易试点，其中，首个碳排放交易所——深圳碳排放权交易所于2013 年正式启动，这表明中国开始了碳交易方面的探索。由于中国在这方面仍处于起步阶段，故对各试点的碳排放权交易价格进行预测和分析，能够为进一步评估中国碳金融市场波动风险以及风险预警提供重要参考。这不仅能帮助政府做出有效的针对性决策，也能更好地服务投资者，并且降低甚至规避其遇到的风险的可能性。而目前针对于碳交易市场的研究主要集中于市场波动评估与风险研究，具体可以分为碳资产收益波动性研究、风险价值度量以及碳排放权交易价格研究等部分。

金融资产的波动性，即其价格的波动程度[1]（或指金融资产价格与市场预期相偏离的程度[2]），与金融资产收益率的确定性呈现反方向变动关系。由于金融市场的波动性伴随时间的推移而变化（时变性），而且现在的波动与未来波动具有相关性，故时间序列模型方法是分析与评估波动率序列的核心方法。波动率能有效反映金融市场的风险程度，是刻画风险的重要指标之一，目前已经有较多相关类型的研究[3-5]。

风险价值（Value at Risk）度量是测定金融市场风险的最普遍且有效的方法，用于衡量在给定持有期和置信水平下，单一资产或资产组合的最大损失[6]，是分位数在金融领域的重要应用。在VaR的众多计算方法中（分析法、历史模拟法与蒙特卡洛法）中，使用分析法计算VaR，能够有效刻画金融资产收益率的数学特征，如基于t 分布和GED 分布的GARCH-VaR 模型、GARCH-EVTVaR 模型[7-8],以及基于SGT 分布族的GAS-VaR 模型[8]等。

碳交易价格研究又可以细分为碳价格的影响因素研究以及碳排放权价格预测等部分：马忠芸（2019）通过Lasso 回归筛选出了影响中国碳排放价格的主要因素，得出空气质量指数等因素对碳价格的影响显著，而化石燃料价格对碳交易价格存在负向影响等结论[9]；吕靖烨等（2019）采用了多元回归分析与主成分分析的方法，对广东省碳交易价格的影响因素进行了研究[10]；还有学者采用了ARIMA 模型对欧洲碳金融期货价格进行了预测，并且根据预测结果提供了相应的策略建议[11]。综上，借鉴之前学者的研究，本文拟构建ARIMA模型，对福建碳排放权市场的日收盘价进行分析，为中国碳交易与碳金融市场的进一步发展及其后续研究提供参考。

2 计量模型——基于经典时间序列分析的模型构建

碳排放权的日交易收盘价数据可以看作是一组时间序列数据。时序数据即某一随机变量按照时间前后产生的一组数据，因此时间序列{ }Xt无法体现多个随机变量的情况，而是体现出单一随机变量在不同时刻的变化。研究时序数据最有效的工具就是时间序列模型。时间序列模型源于1979年Box &Jenkins 总结并延伸前人研究而提出的经典时间序列分析方法[12]，本部分以经典时间序列分析为基础，阐述研究使用的计量模型。

2.1 时序数据的平稳性

平稳性是时序数据的一个重要统计性质，有严平稳和宽平稳两种类型的定义。严平稳所规定的时序数据的平稳性，体现在随机变量的任意有限维分布不随时间而变化的性质，即存在时间序列{Xt}，其观测值序列为{xt}，若对于时间t的任意m个值t1,t2,···,tm∈T，都有任意整数τ，使得[13]：则称时间序列{Xt}具有严平稳性。

宽平稳是弱化的平稳性，若时间序列{Xt} 满足：①μ2=，即时序数据的二阶矩有限；②EXt=μ，即时间序列的均值是一与t无关的常数；③γ(t,s)=γ(0,t-s)=γ(m,m+s-t)，即任意随机变量间的自协方差函数只与时间长度有关；则称时间序列{Xt} 是宽平稳（或弱平稳）时间序列。

2.2 ARMA(p,q)模型与ARIMA( p,d,q)模型

自回归移动平均——ARMA模型是时间序列分析中较为常用的用于处理平稳时间序列的模型，由时序数据经过自回归（AR）和移动平均（MA）两个过程实现。现有一组具有平稳性的时间序列{Xt}，其观测值序列为{xt}，且满足以下结构的模型被称为自回归移动平均模型ARMA(p,q)[13]：

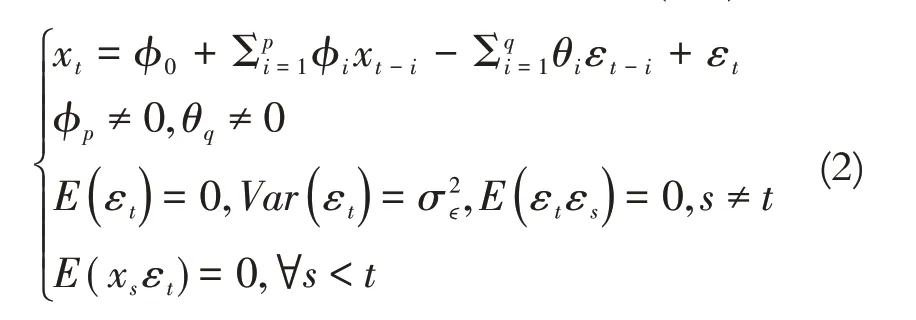
ARMA模型仅仅适用于平稳时序数据，针对不平稳数据需要先进行d阶差分运算。若经过差分处理后的时间序列适用于ARMA 模型，此时称原时序数据适用于ARIMA（p，d，q）模型。

3 实证分析

3.1 数据的选取

研究选取福建碳交易市场的碳排放权（福建省碳排放配额，FJEA）价格的日收盘价作为研究对象，并进行实证研究（数据来源：海峡股权交易中心——环境能源交易平台）。数据选取范围与样本容量如表1。

表1 样本选取范围以及样本容量

3.2 平稳性检验

只有平稳时间序列才能适用于ARMA(p,q)模型，而检验时序数据平稳性的最常用方法是单位根检验，研究则选取了单位根中的ADF(Augmented Dichey-Fuller)检验来判断序列{xt} 是否平稳[14]。研究采用Eviews10对原始时序数据进行ADF检验，检验结果如表2所示。

表2 ADF检验结果（未差分）

检验结果表明，ADF检验的P值大于显著性水平0.05，可以认定存在单位根，时序数据不平稳。因此，需要进行进一步的数据处理，即差分处理。对FJEA日收盘价序列进行一阶差分处理后的时序图如图1所示（软件：SPSS）。

图1 一阶差分处理后的时序图

从差分运算后的时序图可以直观看出，一阶差分后的时序数列具有平稳性。再次对一阶差分后的序列进行ADF检验（检验结果如表3），t检验的p值小于0.05，表明一阶差分后的序列数据具有平稳性。平稳性检验反映了此数据在一阶差分处理后初步适用于ARIMA(p,d,q)模型。

表3 ADF检验结果（一阶差分处理）

3.4 自相关、偏相关分析与模型定阶

3.4.1 自相关（ACF）与偏相关（PACF）分析

平稳性检验结果表明，福建试点的碳排放权交易价格数据在经过一阶差分处理后初步适用于ARIMA(p,d,q)模型。为了更好地确定是否适用于此模型，需要进行自相关与偏相关分析。研究采用SPSS26 软件，对一阶差分后的时序数据进行自相关与偏相关分析（结果如表4），加以观察其函数图像，就可初步定阶p和q。

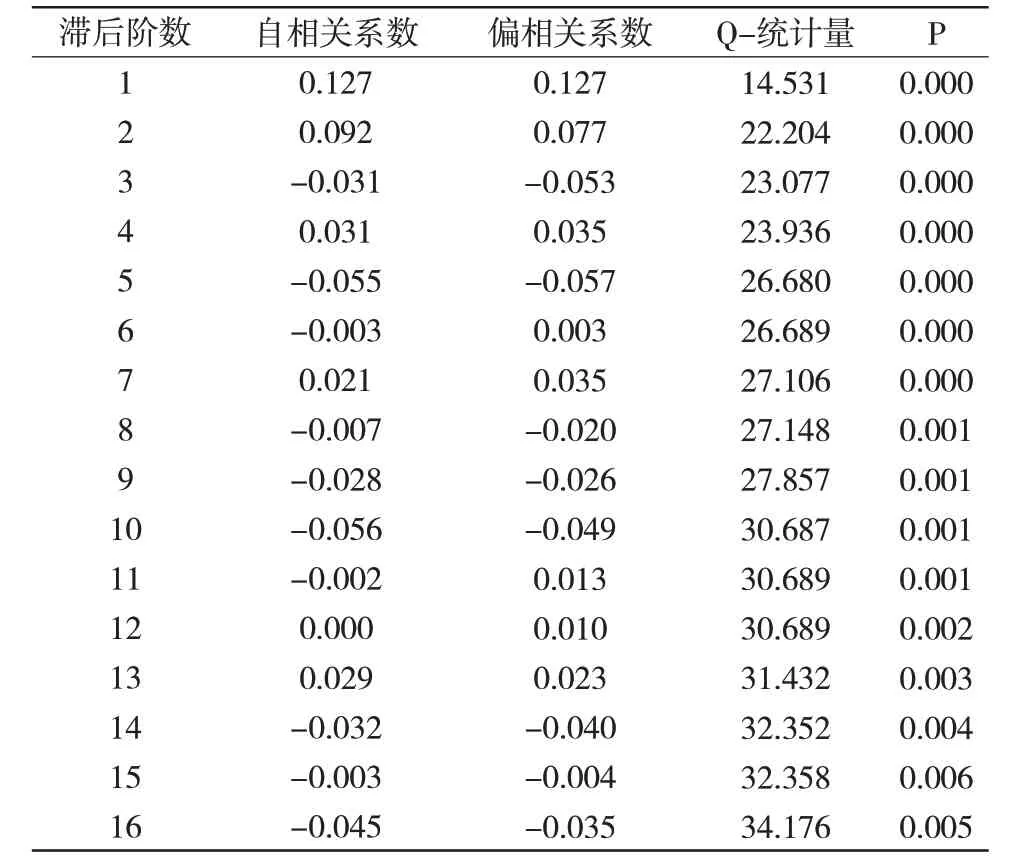
表4 自相关与偏相关分析结果（一阶差分处理）

3.4.2 p和q的定阶

自相关和偏相关系数表显示，自相关系数与偏相关系数均在滞后阶数k=1或2时明显越过显著性边界（5%），而在k=2以后的大部分均落在显著性边界内部，因此判断p和q取到1或2，得到四种模型，分别为ARIMA(1,1,1)、ARIMA(1,1,2)、ARIMA(2,1,1)、ARIMA(2,1,2)。为了选取最适用模型，研究引入贝叶斯信息准则(Bayesian Information Criterion)作为选取依据，BIC值的计算具体如下：

其中：k 表示模型参数个数，L 表示模型得出的最大似然函数值，n是模型中的观测值数量。随着观测值数目的增加，误差也可能随之上升，当BIC值越小，表明模型误差越小，或者说模型对于数据的解释能力越强[14]。模型的检验结果如表5所示：

表5 模型可决系数与BIC值

综上，研究选择ARIMA(2,1,1)作为模型对福建碳交易市场价格进行分析。

3.5 模型检验

3.5.1 拟合优度与模型系数检验

模型结果显示，可决系数R2（即拟合优度）等于0.983，表明模型拟合效果较好。模型的参数估计结果出来后，需要对模型参数进行t检验，模型参数估计值及其t检验结果如表6所示：

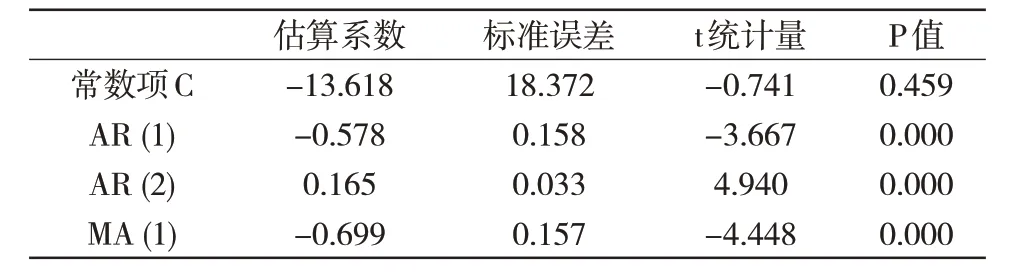
表6 模型参数估计值及其检验结果

模型参数估计表的结果表明，除了常数项C之外，模型各项估算参数的t统计量的概率均小于显著性水平0.05，代表模型ARIMA(2,1,1)通过模型系数检验。

3.5.2 残差白噪声检验

模型有效的另一个标准就是模型残差序列呈现白噪声的性质。研究引入了Box&Pierce 等提出的Q 检验统计量［15-16］对模型ARIMA(2,1,1)的残差序列进行检验（具体原理：Q检验统计量近似服从自由度为m 的卡方分布，当时拒绝原假设，此时该序列不为白噪声序列），检验结果如表7所示：

表7 残差白噪声检验结果

检验结果表明，ARIMA(2,1,1)的残差序列的Q检验统计量（或者Q 检验统计量的概率小于显著性水平0.05），即接受原假设，模型的残差序列为白噪声序列，Q检验通过。

3.4 模型拟合效果

根据上述研究可得，针对福建碳交易市场价格，研究选取了ARIMA(2,1,1)模型，并对观测值样本进行拟合以及进行预测，拟合和预测的部分结果如表8所示。拟合结果表明：①拟合值和实际值间的变化趋势近似；②残差角度，模型噪声残值时序图（图2）显示，模型残差围绕零均值上下波动，表明ARIMA(2,2,1)模型的拟合精度尚可。

表8 模型拟合效果

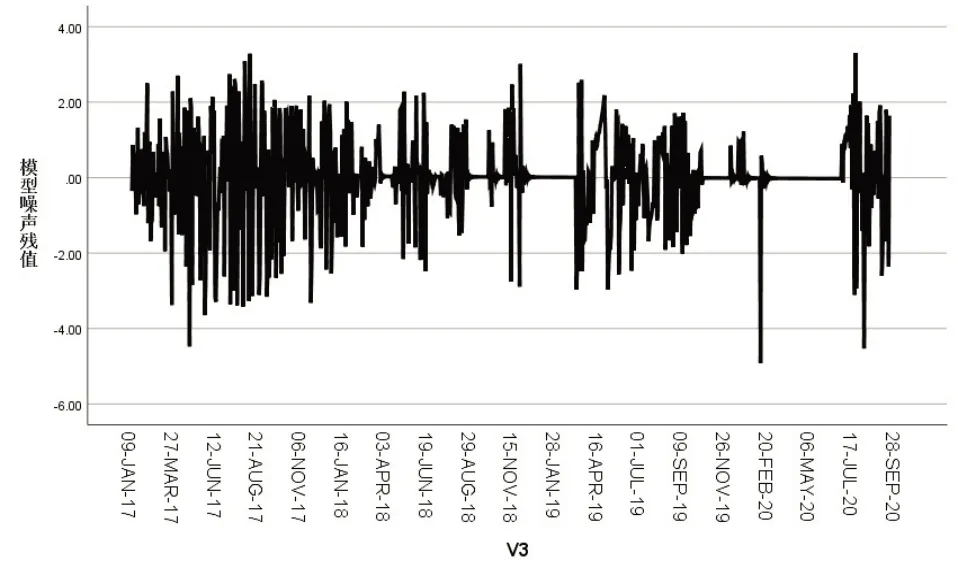
图2 模型噪声残值序列图

4 结论

研究选取了ARIMA(2,1,1)模型对福建的碳排放交易市场价格进行了分析，模型的拟合效果较好，并且能够较为准确地反映碳排放权价格的变动趋势（结果表明，碳排放权日收盘价在短暂上升后会有一段时间的持平期），因此时间序列分析模型在碳排放权价格方面的拟合和预测存在有效性，能够为后续碳金融市场的波动性研究和预警机制构建提供一定的参考。

但是，研究仍然存在着一定的不足：一方面，研究选取的ARIMA 模型残差虽然符合在零均值附近上下波动的特征，但是残差值略大；另一方面，ARIMA 为线性时间序列模型，此研究只是在纯统计角度下进行的，并未考虑到更加复杂的情况。碳金融市场价格是一个非常庞大的非线性系统，碳排放权交易价格会受到多种风险因子的影响。因此，若研究选取的模型要作出更准确的拟合与预测，还需在后续研究中加以改进。