基于机载激光雷达数据的森林蓄积量模型研建

2021-04-02曾伟生孙乡楠王六如

林业科学 2021年2期

曾伟生孙乡楠王六如王威蒲莹

(国家林业和草原局调查规划设计院北京 100714)

激光雷达(light detection and ranging，LiDAR)即光探测与测量，是一种通过发射激光来测定传感器与目标物之间距离的主动遥感技术(赵峰等，2008；李增元等，2016；庞勇等，2019)。按探测目标不同，激光雷达可分为对空和对地两大类，而对地激光雷达按传感器搭载平台不同，又分为星载、机载、车载和定位4类，其中机载激光雷达最为常用(刘鲁霞，2014；李增元等，2016)。机载激光雷达能够获取较大范围森林的三维扫描数据，可用于蓄积量等主要森林参数的估计(赵峰等，2008；刘鲁霞，2014；李增元等，2016)。

在国外，激光雷达用于估计森林蓄积量始于20世纪80年代中期(MacLeanetal.，1986)，经过30多年的研究和实践，激光雷达技术取得了长足发展，尤其是基于机载激光雷达数据估计森林蓄积量的研究已经获得了很多成果(Næsset，1997； Holmgrenetal.，2003； Holmgren, 2004； Hollausetal.，2009； Gonzlez-Ferreiroetal.，2012； Bouvieretal.，2015； Bottalicoaetal.，2017)，为遥感技术在森林资源调查领域的应用开辟了新的途径(Hyyppäetal.，2012； Penneretal.，2013； Whiteetal.，2016； Zörneretal.，2018)。而在我国，激光雷达在林业方面的应用相对较晚(刘鲁霞，2014；李增元等，2016；庞勇等，2019)，目前基于机载激光雷达估计森林蓄积量基本还处于研究阶段，尚未见到具有良好实用性的研究成果(付甜，2010；范凤云，2010；杨明星等，2019)。

森林蓄积量是纳入《绿色发展指标体系》和《生态文明建设考核目标体系》的森林资源约束性指标之一，也是《自然资源调查监测体系构建总体方案》中特别强调的重要森林资源指标。如何充分发挥激光雷达技术优势，服务于新时期森林资源调查监测工作，是当前面临的一项重要课题。具体到基于机载激光雷达数据估计森林蓄积量，尽管国内外已经取得了一些成果，但研建的蓄积量模型仅适用于特定区域，不具有普适性。从森林资源调查的实用性角度出发，研究建立变量相同、结构稳定、在较大地域范围内具有普适性或通用性的模型，是当前需要重点解决的问题(Bouvieretal.，2015)。鉴于此，本研究利用东北林区落叶松(Larixspp.)林、红松(Pinuskoraiensis)林、桦树(Betulaspp.)林、杨树(Populusspp.)林 4种森林类型790个样地的激光雷达数据和地面实测蓄积量数据，首先采用多元线性回归和非线性回归方法，分别建立基于机载激光雷达数据的森林蓄积量回归模型，通过对比分析，确定具有相同变量和统一结构形式的普适性模型；然后采用哑变量建模方法(Zengetal.，2011；郑冬梅等，2013； Zeng，2015)，建立基于相同激光雷达变量的不同森林类型蓄积量模型，以期为规范森林蓄积量建模与评价提供科学参考，为森林资源调查提供计量依据。

1 研究区概况、数据与方法

1.1 研究区概况

东北林区地处黑龙江、吉林和内蒙古 3 省(区)，包括大兴安岭、小兴安岭、完达山、张广才岭、长白山等山系，地理位置119°36′—134°05′E、41°37′—53°33′N，年降水量400～1 000 mm。东北林区是我国森林资源主要集中分布区之一，针叶林主要有落叶松林、樟子松(Pinussylvestrisvar.mongolica)林、红松林和云(Piceaasperata)冷(Abiesfabri)杉林，阔叶林主要有桦树林、栎树(Quercusspp.)林、杨树林、榆树(Ulmusspp.)林、椴树(Tiliaspp.)林和水胡黄林[包括水曲柳(Fraxinusmandshurica)、胡桃楸(Juglansmandshurica)、黄菠萝(Phellodendronamurense)]，另外还有一些混交林类型。本研究从针叶林和阔叶林中各选取2种主要森林类型作为研究对象，其中针叶林选取落叶松林和红松林，阔叶林选取桦树林和杨树林，未考虑结构较复杂的混交林。

1.2 数据资料

1.2.1 地面样地调查数据地面样地调查数据来自821块样地，其中落叶松林202块、红松林200块、桦树林205块、杨树林214块。调查范围覆盖大兴安岭、小兴安岭、完达山、张广才岭、长白山等林区，并选择具有典型代表性的12个片区，调查时间为2019年9—11月。样地为600 m2圆形样地，中心点用RTK技术定位，定位精度在1 m以内。除每株样木测量胸径外，还测量15株不同径阶的样木树高，以此为基础建立树高-胸径回归模型，推算每株样木树高，并依据部颁二元立木材积表计算样木材积，从而得到样地的蓄积量，作为建模的目标变量(Y，m3·hm-2)。

1.2.2 机载激光雷达数据机载激光雷达数据的获取范围与地面样地调查相同，获取时间为2019年9—10月。采用RIEGL-VUX-1UAV型激光扫描系统，其基本参数为：精度10 mm，最大测距范围920 m，最大发射频率550 kHz，最大有效测量速率每秒500 000 次；数据点云密度每平方米大于4个点，现地定位精度0.11 m。在对原始数据进行预处理的基础上，利用商业化专用软件LiDAR360进行激光雷达点云数据的分类、平差以及数字高程模型(DEM)、数字表面模型(DSM)和冠层高度模型(CHM)的处理，最后提取反映林分高度、密度和结构信息的98个变量作为建模的解释变量，其中高度变量56个(X01～X56)、强度变量42个(X57～X98)(为省篇幅，具体含义不详列，后面会对用到的变量给出解释)。

1.2.3 异常数据处理在建模前，对821块样地中的异常数据进行剔除处理。由于涉及的解释变量个数达98个之多，很难逐一绘制目标变量与解释变量之间的散点图来判定和剔除异常数据，因此本研究首先采用全部数据建模，然后根据主要解释变量的残差图来判定和剔除异常数据，并确保剔除异常数据比例不超过5%。最后参与建模的样地数为790块，其中落叶松林197块、红松林197块、桦树林202块、杨树林194块。表1为4种森林类型参与建模样地的林分年龄、平均树高和蓄积量的变动范围。

表1 建模样地主要林分因子的变动范围Tab.1 The ranges of main stand variables for modeling plots

1.3 建模方法

利用4种森林类型790块样地的机载激光雷达数据和地面实测蓄积量数据，基于从特殊到普遍、再从普遍到特殊的建模思路，首先采用多元线性回归和非线性回归方法，分别建立线性和非线性回归模型，通过对比分析，确定具有相同变量和统一结构形式的普适性模型；然后采用哑变量建模方法，建立基于相同激光雷达变量的不同森林类型蓄积量模型。

1.3.1 线性回归模型采用逐步回归方法确定有显著相关的解释变量(付甜，2010； Bottalicoaetal.，2017)，拟合如下多元线性回归模型：

Y=a0+a1X1+a2X2+ … +akXk+ε。

(1)

式中：Y为蓄积量(m3·hm-2)；X1、X2、…、Xk为从98个机载激光雷达信息变量中挑选出来的解释变量；a0、a1、…、ak为模型参数，参数估计值的t值原则上应大于2，否则视为无统计学意义，应从模型中剔除；ε为误差项，假定其服从均值为0的正态分布。

1.3.2 非线性回归模型在线性模型(1)基础上，建立如下非线性回归模型(Bouvieretal.，2015)：

(2)

式中：b0、b1、…、bk为非线性模型参数。

模型(2)参数求解采用非线性加权回归估计方法，以消除异方差的影响。

通过对非线性回归模型和线性回归模型的拟合结果及其评价指标进行对比分析，确定影响森林蓄积量估计的主要激光雷达信息变量，并提出反映普遍规律的模型作为基础模型。

1.3.3 哑变量模型确定普适性基础模型后，由于模型具有相同变量和统一结构形式，不同森林类型的蓄积量模型只是参数估计值存在差异，因此采用哑变量建模方法(Zengetal.，2011；郑冬梅等，2013； Zeng，2015)，同时建立多种森林类型的蓄积量模型。以二元非线性模型为例，其表达式如下：

Y=(∑b0i·Si)·X1(∑b1i·Si)·X2(∑b2i·Si)+ε。

(3)

式中：Si为反映不同森林类型的哑变量(i=1、2、3、4)；b0i、b1i、b2i为不同森林类型参数。

哑变量的赋值方法为：对于落叶松林样地，S1=1，S2=S3=S4=0；对于红松林样地，S2=1，S1=S3=S4=0；对于桦树林样地，S3=1，S1=S2=S4=0；对于杨树林样地，S4=1，S1=S2=S3=0。模型(3)参数求解方法同模型(2)。

1.3.4 模型评价采用确定系数(R2)、估计值的标准误差(standard error of the estimate,SEE)、总体相对误差(total relative error,TRE)、平均系统误差(mean system error,MSE)、平均预估误差(mean predictive error,MPE)和平均百分标准误差(mean percentage standard error,MPSE)对模型进行评价(曾伟生等，2011； Zeng，2015)，其中MPE和MPSE的计算公式如下：

(4)

(5)

对于建立的蓄积量回归模型，计算以上6项指标，根据指标大小进行模型评价。另外，残差图也是评价模型的重要参考依据，一般要求残差呈随机分布。

2 结果与分析

多元线性模型(1)和非线性模型(2)的解释变量个数(k)及6项评价指标见表2。

表2 线性和非线性蓄积量模型的评价指标Tab.2 Evaluation indices of linear and nonlinear stand volume models

由表2可知，2种针叶林类型的非线性模型相比线性模型要简单一些，非线性模型的解释变量只有3或4个，线性模型的解释变量达4或6个； 2种阔叶林类型的线性和非线性模型，都只包含2个解释变量。从评价指标对比来看，2种阔叶林类型均为非线性模型好于线性模型，2种针叶林类型由于线性模型的解释变量个数较多，其R2、SEE和MPE略好于非线性模型，TRE几乎无差异，但MSE和MPSE则为非线性模型明显好于线性模型，且这2项指标几乎所有线性模型均出现异常情况，究其原因是估计值出现极小值甚至负值导致的。综合来看，非线性模型(2)的拟合效果要好于线性模型(1)，因此优先考虑采用非线性模型，其具体拟合结果见表3。

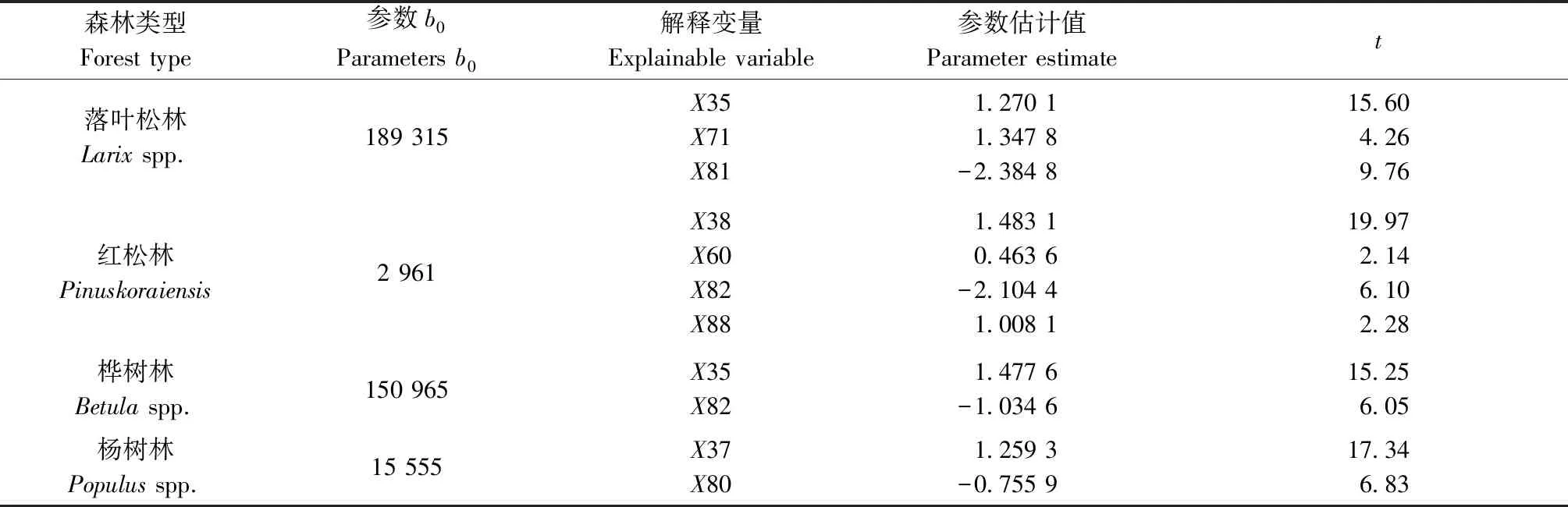
表3 非线性蓄积量模型(2)的拟合结果①Tab.3 Fitting results of nonlinear stand volume model(2)

关于非线性模型(2)，4种森林类型中有2种仅包含2个解释变量，一是点云高度变量(X35或X37)，二是点云强度变量(X80或X82)。如果将落叶松林和红松林的非线性模型从三元和四元模型简化为二元模型，其R2分别从0.727、0.818减至0.676、0.805，MPE分别从3.95%、2.89%增至4.29%、2.97%。从模型简约性和实用性考虑，这样的变化幅度是可以接受的，因此选定二元非线性模型作为统一形式的蓄积量模型。

进一步分析二元模型中包含的点云高度变量和强度变量，一个为显著正相关变量(X35、X37或X38)，一个为显著负相关变量(X80、X81或X82)。将4种森林类型790块样地数据合在一起进行相关分析发现，正相关最大的变量为X35(点云平均高度)，负相关最大的变量为X90(点云平均强度)，表4为正负相关最大的各10个变量。

表4 与蓄积量正负相关最大的20个激光雷达变量Tab.4 20 LiDAR variables having the greatest positive and negative relation with stand volume

从表4可以看出，正相关最大的10个变量集中分布在3个区段：X35～X37(点云高度平均值、二次幂平均值、三次幂平均值)、X23～X26(点云高度50%、60%、70%、75%分位数)、X06～X08(点云累积高度30%、40%、50%分位数)；负相关最大的10个变量也集中分布在3个区段：X90～X91(点云强度平均值、中位数)、X77～X83(点云强度30%、40%、50%、60%、70%、75%、80%分位数)、X46(点云高度偏斜度)。尤其需要重点关注的激光雷达变量，是位于正负相关2个顶端的变量X35和X90。利用790块样地数据拟合基于X35和X90的二元模型，其R2达0.790，高于落叶松林、桦树林和杨树林3类蓄积量模型的R2，仅低于红松林模型的R2。由于X35和X90是最符合预期的激光雷达点云信息变量，故本研究将基于这2个变量的二元蓄积量模型定义为标准模型，其相应的哑变量模型为：

Y=(∑b0i·Si)·X35(∑b1i·Si)·X90(∑b2i·Si)+ε。

(6)

取1/X35为权函数，采用加权回归方法拟合哑变量模型(6)，其R2达0.866，4种森林类型的参数估计值和模型评价指标见表5。

表5 哑变量模型(6)的参数估计值和模型评价指标Tab.5 Parameter estimates and evaluation indices of dummy model(6)

由表5可知，采用变量相同、结构统一的标准二元模型估计4种森林类型蓄积量，其效果与表2中模型(2)差异不大，模型参数值大小也较一致，说明该模型稳定可靠，具有普适性；而表3中不同森林类型的非线性模型(2)不仅变量个数有差异，而且参数值也相差悬殊。另外，表5中4种森林类型蓄积量模型残差随解释变量分布基本是随机的，图1、2所示为落叶松林和红松林蓄积量模型相对残差随解释变量X35的分布情况，图3、4所示为落叶松林和红松林加权回归模型残差随解释变量X35的分布情况，反映了消除异方差后的效果(桦树林和杨树林模型残差也相似，此处略)。

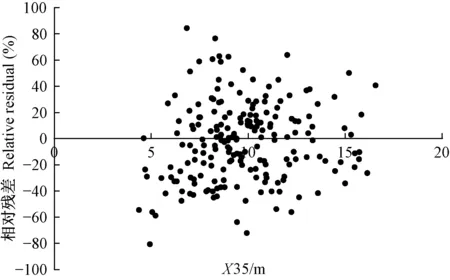
图1 落叶松林蓄积量模型的相对残差分布Fig. 1 Relative residual distribution of stand volume model for Larix spp.

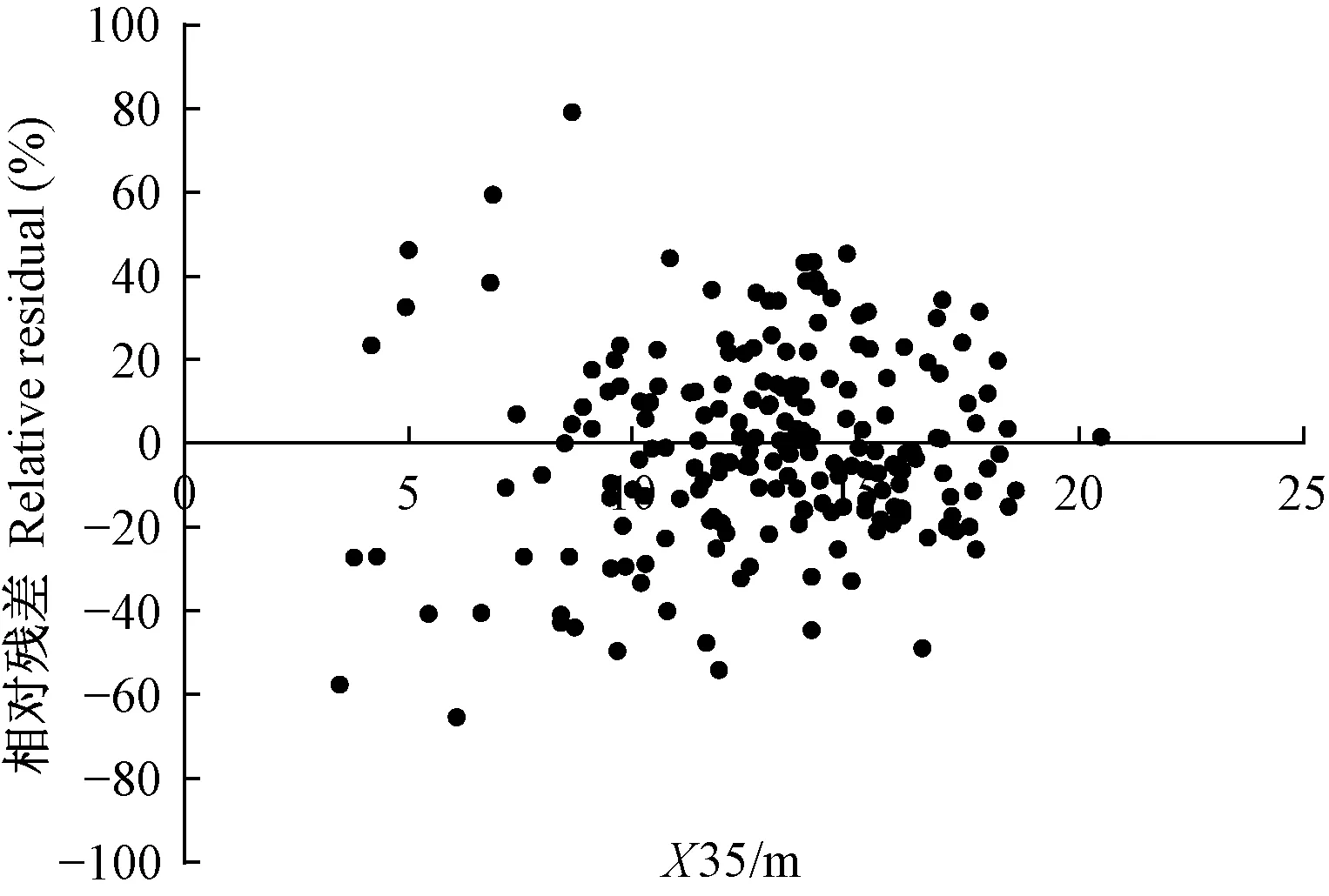
图2 红松林蓄积量模型的相对残差分布Fig. 2 Relative residual distribution of stand volume model for Pinus koraiensis

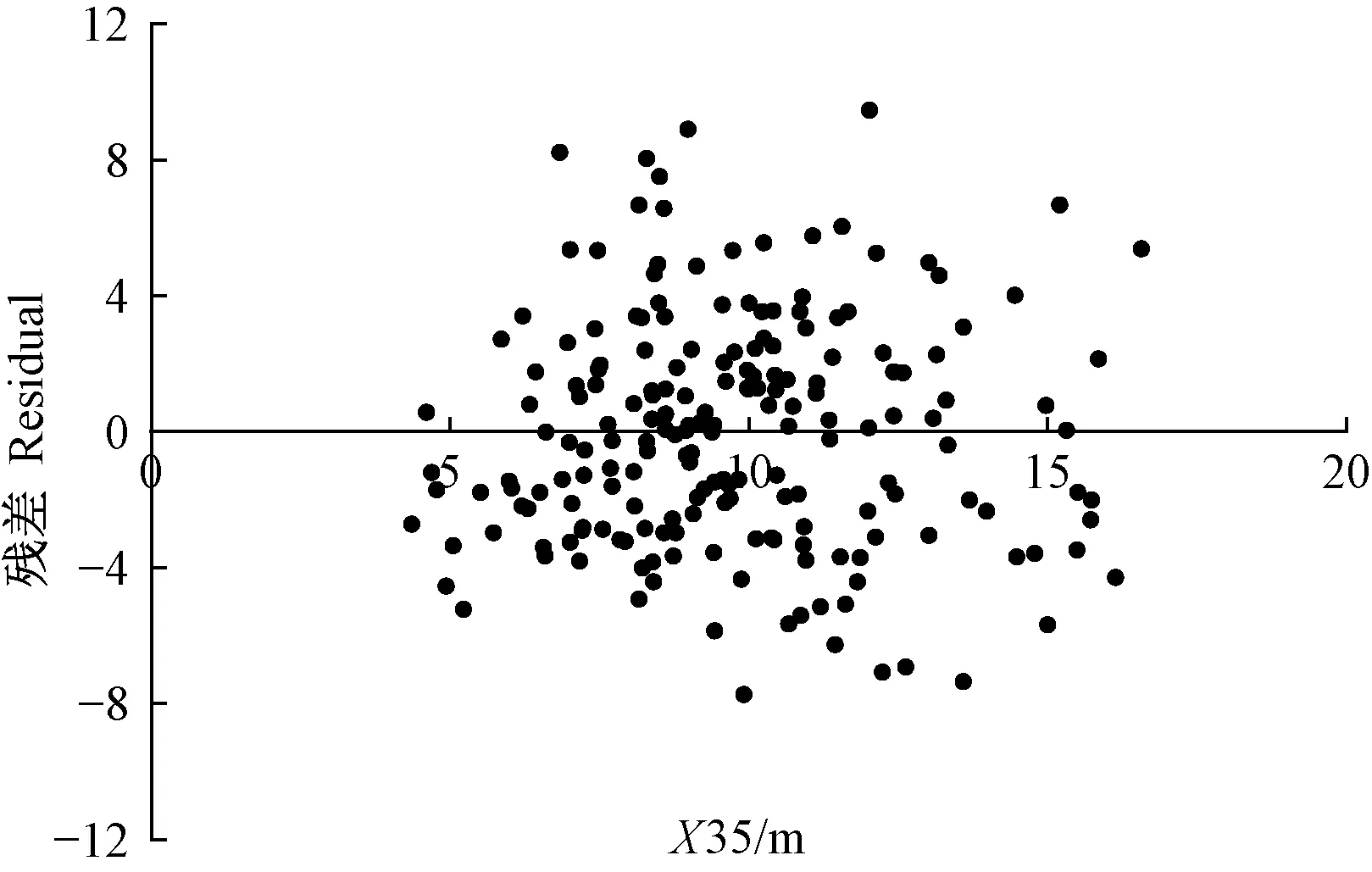
图3 落叶松林加权回归模型的残差分布Fig. 3 Residual distribution of weighted regression model for Larix spp.

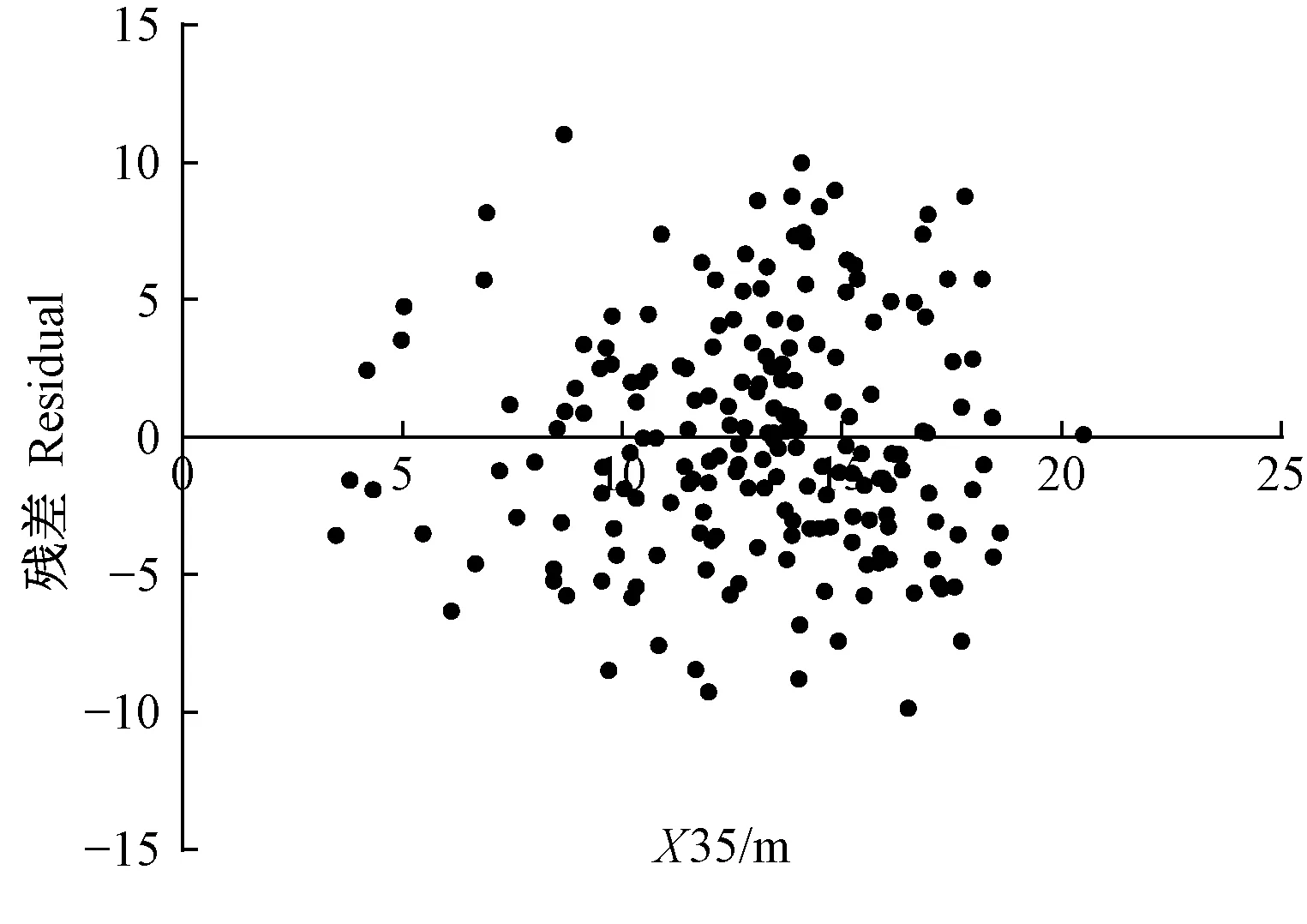
图4 红松林加权回归模型的残差分布Fig. 4 Residual distribution of weighted regression model for Pinus koraiensis

3 讨论

激光雷达作为一种主动遥感技术，为高效估计森林蓄积量、提高森林资源调查监测工作效率提供了可能(赵峰等，2008； Hyyppäetal.，2012； Penneretal.，2013； Whiteetal.，2016)。利用激光雷达技术估计森林蓄积量的研究最早可追溯到20世纪80年代(MacLeanetal.，1986)，我国将激光雷达技术应用于森林蓄积量、生物量方面的估计相对较晚，尽管近10年来已取得了一些研究成果(付甜，2010；范凤云，2010；庞勇等，2012；刘清旺等，2016；杨明星等，2019)，但具有良好实用性的成果不多，也尚未形成基于激光雷达技术估计森林蓄积量的应用技术规范。本研究结合我国现阶段的信息需求，从森林资源调查监测最关注的蓄积量因子入手，提出了变量相同、结构形式统一的普适性模型，并基于哑变量建模方法，建立了东北林区4种主要森林类型的蓄积量估计模型，模型的确定系数(R2)在0.68～0.81之间，略低于Holmgren(2004)研建的2个蓄积量模型(R2分别为0.82和0.90)，与Hollaus等(2009)建立的2个蓄积量模型(R2分别为0.79和0.81)基本一致，与Bottalicoa等(2017)建立的针叶林和栎树林蓄积量模型(R2在0.69～0.83之间)也较接近。当然，模型的拟合精度与森林结构、研究区大小也是密切相关的。

森林蓄积量模型R2高低，在很大程度上还取决于从激光雷达数据中提取的信息变量。激光雷达信息变量包括不同分位数高度、不同分位数密度和最大回波高度等，但不同研究选择的变量不尽相同(刘鲁霞等，2014)。本研究提取反映点云高度和强度的98个变量建立蓄积量回归模型，进入多元线性模型的变量2～6个，进入多元非线性模型的变量2～4个。从分析可知，反映林分高度的变量是最重要的，而在众多高度变量中，体现点云平均高度的变量与蓄积量相关性最高；点云强度变量在一定程度上反映了林分的疏密状况和水平结构特征，与蓄积量大小呈负相关，即林分高度相同时，株数越多林分越密，蓄积量就越大，点云强度就越小；株数越少林分越疏，点云强度就越大。从实用性角度出发，非线性二元模型与多元模型没有实质性差异，而二元模型采用的解释变量为X35(点云高度平均值)和X90(点云强度平均值)，这既是全部98个变量中正负相关最大的2个变量，也是最符合预期的2个变量，所以本研究将基于这2个变量的二元蓄积量模型定义为标准模型。范凤云(2010)基于激光点云数据提取了林分高度平均值、最大值、最小值、标准差4个变量，建立油松(Pinustabulaeformis)和刺槐(Robiniapseudoacacia)的林分蓄积量回归模型，其唯一的解释变量就是林分高度平均值； Bouvier等(2015)建立了基于4个变量的通用性模型，其中影响最大的变量是平均冠层高度，与点云平均高度类似； Bottalicoa等(2017)提取了49个变量作为森林蓄积量等主要参数的解释变量，所建森林主要参数回归模型的变量在1～4个之间，其中与蓄积量相关性最大的变量是点云高度平均值和三次幂平均值，与本研究结果基本一致。

森林蓄积量模型的实用性主要取决于平均预估误差(MPE)和平均百分标准误差(MPSE)的大小，前者衡量对总体蓄积量的估计误差，后者衡量对样地或林分水平蓄积量的估计误差。本研究建立的4种森林类型蓄积量模型，MPE在2.89%～4.25%之间，均未超过5%； MPSE在18.13%～24.43%之间，其中红松林小于20%，其他3种森林类型小于25%。《森林资源规划设计调查技术规程》(国家质量监督检验检疫总局等，2011)对小班调查公顷蓄积量的精度分A、B、C三级，要求误差分别不超过15%、20%和25%。可见，红松林蓄积量模型可以满足B级精度要求，其他3种森林类型蓄积量模型可以满足C级精度要求。采用传统调查方法要达到上述技术规程的精度要求是非常费工费力的，而利用激光雷达技术构建的蓄积量回归模型，只需提取相关信息变量就能得到有一定精度保证的蓄积量估计值，因此利用激光雷达技术开展森林资源规划设计调查在技术上是可行的。