矮化密植果园多臂采摘机器人任务规划

李 涛，邱 权※，赵春江，谢 丰,3

（1. 北京市农林科学院北京农业智能装备技术研究中心，北京 100097；2. 北京市农林科学院北京农业信息技术研究中心，北京 100097；3. 江苏大学农业工程学院，镇江 212000）

0 引言

中国是世界最大水果生产国和消费国，预计2025年水果行业市场规模将达到27460.1亿元左右[1]。然而国内水果生产综合机械化率与发达国家相比仍较低，仅为28.6%，特别是采摘阶段，采摘机械化率不足3%[2]。随着劳动力成本的上升和人口老龄化问题的加剧，鲜果产业发展面临瓶颈[3]。

近年来，矮化密植栽培标准果园规模不断扩大，为果园智能化、机械化作业提供了有利条件，采摘机器人与新型农艺相结合成为水果产业发展新趋势[4]。目前，果园采摘机器人研究在果实识别定位[5]、路径规划[6]、位姿调节[7]、柔性抓取[8]等方面取得了积极进展。但总体而言，仍普遍存在效率低的问题，难以满足鲜果采摘的实际需求[9]。特别是在矮化密植标准果园规模采摘的需求背景下，提升采摘机器人作业效率迫在眉睫。

针对作业效率问题，Williams等[10]研究了具有4个3自由度（Degree of Freedom，DoF）串联关节型机械臂的猕猴桃采摘机器人，协同开展采摘作业，并能有效避免各机械臂间碰撞；Fu等[11]研制了具有4个3DoF直角坐标机械臂的猕猴桃协同采摘机器人；西班牙AGROBOT公司的草莓采摘机器人[12]配备了24个机械臂，同时开展作业；以色列苹果收获机器人FFRobotics[13]具有4个采摘机械臂，可实现1 s/个的采摘速度。使用多机械臂来提高作业效率，已成为领域内研究者的共识[14]。

不同于单臂采摘机器人，多臂协同采摘的突出挑战是如何根据果实分布情况对各臂任务进行合理规划和调度以有效提升工作效率[15]。为此，一些研究者根据目标分布划分相互独立的作业区域，并分配不同机械臂进行作业[16-18]。例如：针对簇状生长特征明显的作物，研究者通过果实分布聚类情况来划分不同臂的作业范围。Williams等[16]提出的奇异果多臂协同采摘机器人，以二维水平欧式距离为判断标准，对果实进行聚类，并据此为各个机械臂的任务分区；Fu等[11]采用改进K-means的方法对奇异果果簇分布进行聚类。上述研究均假定多臂机器人可到达视野范围的各个区域，对于其他簇状生长特征并不明显的果实，上述方法存在初始聚类中心难以选取的问题[17]。另一类多臂协作方式为直接对多臂作业空间进行分离，使各臂能够各司其职，工作区域互不交叉[12-13,18]，这种方式有效避免了不同机械臂的冲突问题，可实现多臂并行工作。然而，这类机器人各臂的实际工作范围受几何结构或运动学的限制，存在各臂均不可达的作业区域，导致漏采。

随着采摘规模、机械臂数量和作业范围的增加，死区、漏采和各臂冲突等问题愈加突出[19]，多臂作业空间解耦与采摘死区间存在着矛盾关系。为解决死区问题，需将各臂的作业区域进行适度重叠，即每个机械臂既有专属的采摘作业范围，也有共同的采摘区域，从而实现作业范围完全覆盖。

多机械臂采摘不同区域的果实可视为一类旅行商调度问题，但由于重叠区域的存在以及避免多机械臂冲突的需求，传统旅行商问题[20-21]（Travelling Salesman Problem，TSP）和多旅行商问题[22-23]（Multiple TSP，MTSP）难以适用。为此，本文提出异步重叠访问域的旅行商问题（Asynchronous Overlapped MTSP，AOMTSP），解决重叠访问域和多个旅行商同时进入重叠域的冲突。遗传算法（Genetic Algorithm，GA）是求解TSP及MTSP问题的重要方法，已得到诸多成功应用。

鉴于此，本文基于AOMTSP研究矮化密植果园多臂采摘机器人的协同作业任务规划问题，参考MTSP建立0-1规划数学模型，基于GA提出AOMTSP的求解方法。通过面向矮化密植果园的多臂直角坐标机器人系统，研究基于AOMTSP-GA的多臂协作机器人作业任务规划策略，以避免重叠域内多臂冲突，确保机器人以最短时间遍历作业范围内的所有目标果实，提高作业效率。

1 多臂协同采摘机器人作业任务规划

本文研究对象为基于直角坐标系的多臂采摘机器人，如图1所示，主要应用于矮化密植果园。该机器人在机械结构上由4个直角坐标机械臂构成，各单元包含X、Y、Z方向共3个直线模组和旋转关节。末端装配果梗果实分离机构和果实传输波纹管。机器人总体结构参数如图1所示。

当直角坐标机械臂单元的各直线模组XYZ主轴夹角为90°时，各采摘单元的作业范围在空间上互相分离，可开展并行作业。但在各机械臂相邻作业区域的衔接处，受几何结构的限制存在不可达作业区，如图2所示，形成采摘死区，导致漏采。

为解决采摘死区问题，需扩展各执行器可达范围，使各臂作业区域均能覆盖采摘死区。针对本文的多臂协同采摘机器人，对机器人结构进行如下改进：1）将X轴改为上下贯通的共享导轨，使上下2个机构可共享中间区域，形成重叠采摘区；2）将Z轴和Y轴导轨增加旋转机构，使其可左右调节，形成一定的夹角，当左右两侧对准中间区域时，可形成重叠采摘。采摘作业时，为减少总行程、提高作业效率，避免各机械臂在同时访问重叠域时发生冲突，须合理规划各机械臂采摘任务，并遵从如下规则：

1）果实仅能被1个机械臂采摘，摘取后其他机械臂不必访问该果实位置；

2）不限制机械臂对专属采摘区和重叠采摘区内果实的摘取顺序，允许各臂竞争重叠区域内的所有可达目标；

3）限制2个及以上机械臂同时进入重叠采摘区；

4）不限制各臂的初始采摘果实目标，各机械臂在果实间行进速度相同，总遍历时间不包含机械臂摘取果实（即停留在果实目标处）的时间；

5）所有果实目标摘取结束后，遍历总时长最短。

为保证本文任务规划方案的合理性，提出如下前提和假设：

1）假设视觉感知系统能够准确检测并定位果实的三维空间位置；

2）不考虑被叶片完全遮挡的果实；

3）多机械臂协同作业任务规划阶段不考虑机械臂在不同果实间切换时的路径差异，认为果实间的切换时长与其欧式空间距离为线性关系，且速度因子不变。

由于深度卷积神经网络具有出色的表征提取能力和学习能力，结合深度传感器、多线激光雷达等先进传感器，目标果实的检测定位并不困难，但完全或近似被完全遮挡的果实感知问题仍未有有效的解决方案。而矮化密植标准果园的冠层充分窄化，果实分布近似于“果墙”，果实拓扑结构简单，避障动作易实现。

2 异步重叠访问域多旅行商问题描述与求解

2.1 问题描述

根据本文任务规划规则可知：专属作业区访问规则约束与传统旅行商问题（Travelling Salesman Problem，TSP）类似（规则5））；多个机械臂的重叠采摘域分配问题与多旅行商问题（Multiple TSP，MTSP）类似（规则1）、2）和5）），但简单混合TSP和MTSP难以满足规则3）、4）约束。鉴于此，本文提出异步重叠访问域多旅行商问题（Asynchronously Overlapped Multiple Traveling Salesman Problem，AOMTSP），具体描述如下：

设存在N个分布于不同位置的城市，C={1,...,N}表示所有城市的集合，并包含M+S个互不相交的子集，即有其中{Cm,m=1,...,M}表示M个专属城市集的集合，{CS,s=M+1,...,M+S}表示S个共享城市集的集合。考虑M个旅行商依次访问所有城市，要求第m个专属城市集仅能被第m个旅行商访问，第s个城市集可被某2个及以上旅行商访问，并假设各旅行商由某一城市到下一城市时以恒定速度沿直线行走，各旅行商在城市停留时长为Thold，确定M个旅行商完全遍历N个城市的访问序列，使所有旅行商遍历所有城市的总时长最短，且共享城市仅可被游历1次；相邻2个旅行商同时访问其对应的共享城市集合中城市时，排队等候时间为Tw。

为统一术语，将果实记作城市，机械臂记作旅行商。假设作业区域内有36颗果实，按图3分布，4个采摘臂协同作业，则各集合元素示例如表1所示。

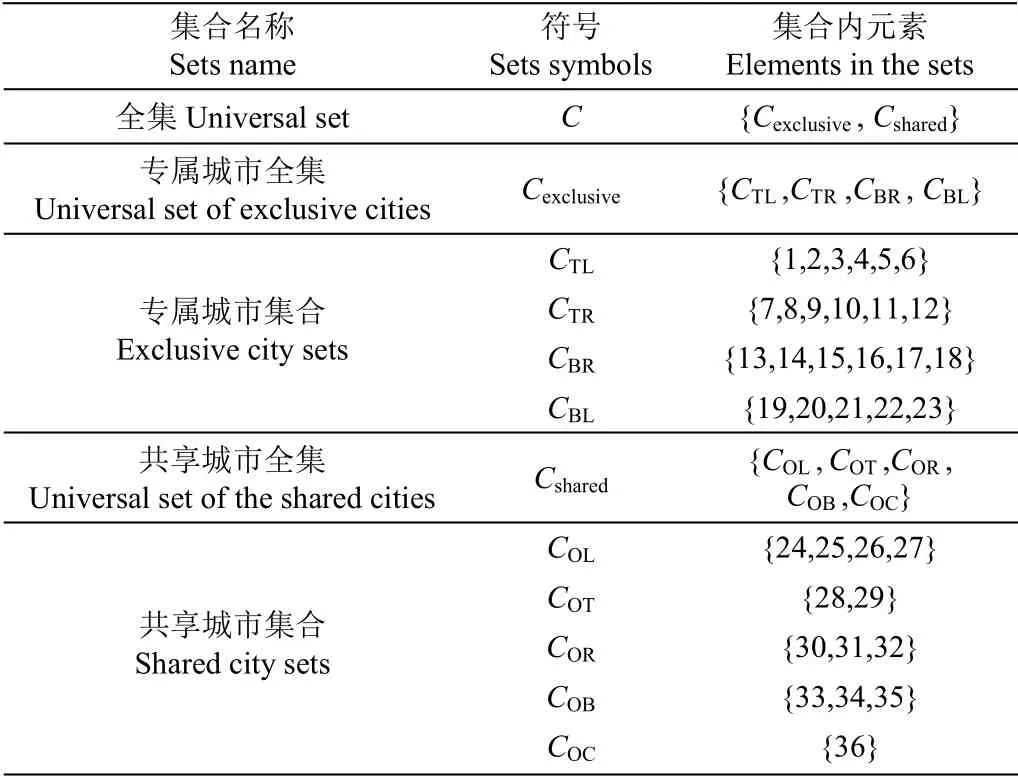
表1 异步重叠访问域多旅行商问题示例 Table 1 Examples of Asynchronously Overlapped Multiple Traveling Salesman Problem (AOMTSP)

2.2 求解方法

本文提出基于遗传算法的AOMTSP求解方法，以下记作AOMTSP-GA。首先确立符合约束条件的编解码方案；然后遵循经典GA的选择、交叉和编译算子对编解码方案进行种群迭代，最终形成符合预期的访问序列。

2.2.1 AOMTSP-GA染色体编码

AOMTSP-GA的染色体是AOMTSP解的表达形式，不同的染色体唯一确定各臂对多目标的采摘访问序列[24]。选取恰当的染色体编码方案是AOMTSP-GA的关键。

传统MTSP方案常选用间隔点方法区分不同旅行商的序列段，但由于AOMTSP存在重叠访问域，传统MTSP方案无法正确描述。为此，本文提出双染色体编码方案：先将一组城市编号的有序数组构造为城市染色体，再将一组旅行商编号的有序数组构造为与城市染色体等长的旅行商染色体，旅行商序号指示城市染色体中对应位置的城市所属关系集合。在不颠倒各旅行商访问序列顺序的前提下，4个旅行商所访问城市编号任意穿插，形成城市染色体；根据城市与旅行商的对应关系，依次列出旅行商染色体数组；根据旅行商染色体中的序号，依次读取城市染色体相应位置上的城市编号，顺序存入该旅行商访问序列数组中，解码各旅行商访问次序。

2.2.2 选择算子

选择算子将优化的个体直接传到下一代或将配对交叉产生的新个体遗传到下一代。常用的选择策略包括基于适应度比例（轮赌盘策略）、基于排名、基于局部竞争机制（锦标赛策略）、最佳个体保存等策略[25]。其中最佳个体保存策略收敛性较好，轮赌盘策略可避免局部最优[26]。

为提高算法收敛速度，同时提高全局搜索能力，本文采用最佳个体保存与轮盘赌选择相结合的策略。首先对每代种群所有个体计算适应度并按照适应度排序，保留适应度最佳的个体，直接传入下一代；剩余个体采用轮盘赌选择策略产生，并传入下一代。

2.2.3 交叉算子

交叉算子将2个父代个体的部分结构重组生成新个体[27]，以提高GA 的搜索能力。首先采用部分匹配交叉（Partially Matched Crossover，PMX），交叉2个父代城市染色体，然后利用旅行商染色体检测交叉后的专属城市分配，查看是否符合专属访问区约束。首先随机生成2个位串交叉点，定义这2个点之间的区域为1个匹配区域，随后交换2个父代城市染色体的匹配区域，最后检测交换后的2个父代染色体匹配区域外元素是否与匹配区域内重复，若重复则逐一替换为匹配区域内对应的元素。

2.2.4 变异算子

变异算子负责对城市染色体和旅行商染色体内的编码进行变异[28]。变异算子包含若干种不同的变异操作以维持种群的多样性，防止过早收敛。首先随机生成2个基因位置分别作为变异段的起止位置，随后分别采用翻转、交换、滑动来重排城市基因段；旅行商染色体变异的实质是对共享城市集内城市的旅行商映射进行再分配。

2.2.5 异步规则

为满足任务规划规则3），避免不同旅行商同时访问1个共享城市集，需加入异步规则，增加排队时长，以还原多机械臂任务规划过程中2个或2个以上旅行商访问1个共享区域的等候过程。

异步规则的关键在于建立旅行商时间表。首先定义专属城市集合内各城市间距离如下：

式中dTL，dTR，dBR和dBL为旅行商TL、TR、BR和BL的专属城市区域距离向量；2,1d为城市1至城市2的距离，共享城市区域距离向量dOC,… ,dOR也可得到。

然后根据城市间距离计算旅行商访问时间。假设旅行商TL已依次访问专属城市1～6，正在访问共享城市26，从起点开始计时，则当前时刻为

接下来检查各旅行商访问相同共享城市集内城市的时刻，查看是否有交叉，若存在交叉则需为旅行商增加排队等候时间Tw。按照时间先后，规定后访问共享城市集的旅行商需等待Tw，并更新该旅行商的时间表。重复上述步骤，反复检查并更新各旅行商时间表，直至各旅行商时间表中均不存在共享城市集内的交叉访问。

由于排队时间的增加将直接导致总耗时的增加，因此异步规则中所设定的排队约束条件是一个惩罚性约束，以引导算法向排队时间和总耗时更短的方向进化。

2.2.6 适应度计算

AOMTSP优化目标为各旅行商遍历各城市的时间总和最小。在考虑规则4）、规则3）和优化目标的前提下，设计适应度函数F(x)为

式中c为旅行商行进速度，m/s；f(x)为当前访问序列下的总路径长度，m；n为旅行商同时访问相同共享城市集合的次数。由式（3）可知，适应度越大表明个体的性能越好，AOMTSP的优化目标为适应度函数F(x)的函数值最大[29]。

3 基于AOMTSP-GA的多臂采摘协同任务规划试验

3.1 双臂协同采摘机器人软硬件系统集成

本试验基于图4所示的多臂采摘机器人硬件平台进行，包括：1）2组直角坐标机械臂。每组机械臂具有3个平移自由度和1个旋转自由度，重复定位精度为±0.02～0.05 mm，有效行程为X轴650 mm、Y轴650 mm、Z轴450 mm，R轴±30°，有效载荷10 kg，运行速度50 mm/s，其中各关节电机采用直流伺服电机驱动，基于CANOpen总线协议控制，X轴、Y轴电机功率为750 W，Z轴电机功率为400 W，R轴电机功率为100 W；2）支撑框架为80 mm×80 mm铝制型材，长×宽×高为2 m× 0.6 m×0.46 m；3）深度相机为英特尔Realsense D455，采用红外双目立体感知技术，最高分辨率为1280像素×720像素，深度测量范围为0.4～6 m，全局快门，数据接口为USB3.0 Type-C；4）嵌入式计算机为NVIDIA Jetson TX2，NVIDIA PascalTM架构，图形处理器单元为NVIDIA MaxwellTM，有256个CUDA内核，中央处理器单元为Quad ARM®Cortex-A系列A57。

嵌入式计算机TX2操作系统为Ubuntu 18.04。本试验中机器人采用ROS-Melodic进行控制系统开发，机械臂运动规划使用ROS-Moveit!功能包。图5为ROS-Moveit!的双臂协同采摘机器人控制系统示意图。

为验证本文AOMTSP-GA任务规划算法在实际机器人系统中的有效性，基于上述机器人软硬件平台，开展协同任务规划试验。具体试验内容包括：1）果实检测与定位试验，以验证视觉检测与定位系统的有效性；2）根据前期矮化密植果园调研结果，本文机器人平台作业范围内果实数量为20～90 颗，平均约为43颗，因此试验分别选取43（平均数）和90颗果实2种情况，开展任务规划仿真试验，检验本文AOMTSP-GA的收敛情况及任务规划性能；3）基于多臂机器人平台开展实际试验，验证本文所提方法在3种不同果实分布情况下的AOMTSP-GA任务规划效果。

3.2 果实目标检测与定位试验

试验在实验室和实际果园2种环境中开展，实验室环境中采摘面长1.8 m、高2.2 m、冠层深0.1 m，如图6a所示。实际果园位于北京市昌平区天汇园，果树品种为SH6矮化中间砧型富士苹果，采摘面高约2.8 m、冠层深0.4 m，如图7a所示。

多臂协同采摘感知系统硬件平台采用Realsense D455深度相机进行图像采集，NVIDIA Jetson TX2作为图像边缘计算单元。首先基于YOLOV5深度卷积神经网络模型开展，通过深度相机RGB图像对果实进行多目标在线检测；得到RGB图像检测结果后，在对齐的深度图中提取果实区域的深度信息，并结合相机内参矩阵求取果实目标的三维空间位置，进而得到所有目标果实的三维空间分布情况，识别结果如图6b和图7b所示。

为便于采摘的任务规划，对目标果实识别与定位结果根据本文任务分区方法（图3）作进一步划分，得到如图6c和图7c所示的作业区域。

3.3 多臂协同采摘机器人任务规划仿真试验

采用AOMTSP-GA和随机遍历2种算法分别进行2组仿真试验，具体参数设置如表2所示，目标果实的分布方案如图8a、图9a、图10a所示，试验结果如表 3所示。

43颗目标果实的规划试验结果表明，相较于随机遍历算法，AOMTSP-GA算法的采摘任务规划作业遍历时长缩短40.97%，遍历路径如图8b所示；算法迭代500次收敛，如图8c所示。90颗目标果实的试验中，相较于随机遍历算法，2种参数条件下的AOMTSP-GA算法作业遍历时长分别减少44.53%和54.98%，遍历路径分别如图9b和图10b所示。如图9c和图10c所示，适当增大种群数量和交叉变异比参数，可使优化解更接近于全局最优解，但算法收敛的迭代次数和求解时间也相应增加。

为说明多臂协同采摘相比于单臂的优越性，采用顺序遍历的采摘方案，以单机械臂采摘90颗目标果实作为对比。试验中设单臂单果采摘单次耗时3 s，末端执行器行进速度1 m/s。结果表明：单臂作业的采摘总耗时约为270 s，遍历路径规划总耗时约为140 s，合计总时长约为410 s；单臂采摘方案总耗时约为多臂AOMTSP-GA算法的4.28倍。

表2 多臂协同规划算法参数取值设置 Table 2 Configuration of parameters in the multiple manipulator cooperatively planning algorithm

表3 不同果实分布方案下4臂协同采摘机器人任务规划仿真试验结果 Tabel 3 Simulation results of task planning of 4-arm cooperative picking robot under different fruit distribution schemes

3.4 双臂协同采摘机器人多目标采摘试验

为验证本文AOMTSP-GA任务规划算法在实际机器人系统中的有效性，基于图4所示双臂协同采摘机器人硬件平台开展实际采摘任务规划试验。

首先按照统一机器人描述格式（Unified Robot Description Format，URDF）编写机器人模型描述文件，并基于ROS-Moveit!系统[30]配置运动学规划器，并建立双臂协同采摘机器人控制系统；然后将AOMTSP-GA算法部署于ROS分布式通讯系统内，初始化规划器节点，该节点以话题形式订阅果实多目标三维位置信息，并通过回调函数实时计算左右2个臂的果实采摘遍历顺序，然后以话题形式将目标果实的序列信息发布；配置左右2个机械臂控制节点分别订阅规划器节点发布的采摘序列话题，调用Moveit!运动规划组求解运动学逆解，生成各关节位置、速度、加速度轨迹点，形成左右臂2个运动学组的动态轨迹，驱动双臂各自抵达当前笛卡尔目标位置；当左右2个机械臂抵达当前果实目标位置后，反馈执行结果至规划节点，规划节点更新采摘序列话题，以话题形式发布下一目标果实位置信息，并重复上述步骤，直至完成所有果实的遍历。

基于ROS-Moveit!开发双机械臂运动规划器，使用开源OMPL（Open Motion Planning Library）机器人运动规划库。OMPL涵盖当前最新的机器人运动规划算法，适用于高维空间和复杂约束下的机器人路径求解，可避免高维度机械臂规划中的维度爆炸问题。几何约束及运动学约束配置如下：1）根据规划分区和X滑轨尺寸，设置2个机械臂的沿X轴最大活动范围为0～1 m；2）由于结构限制，将第三连杆所装配的旋转滑台活动范围限制为60°。完成OMPL规划器配置后，添加规划请求适配器组，为轨迹路点配置速度和加速度参数，形成动态运动轨迹。运动学逆解器采用IKFast，该求解器得到的运动学逆解为封闭解，求解速度更快并支持零空间解，是目前求运动学逆解的先进算法。此外，考虑到矮化密植果园园艺特征[31]，试验中不在工作空间添加障碍物，将柔性枝叶视为可碰撞物体。

按照2个机械臂左右分布，划分左侧专属采摘区域L、右侧专属采摘区域R和重叠采摘区O，按照由均匀到集中的3种果实分布分3组进行试验：试验1果实分布相对稀疏、均匀，L区分布11颗果实，R区分布5颗果实，重叠区域O分布12颗果实；试验2果实分布较为集中，L、R、O各区果实数量分别为6、6和16；试验3果实分布最为集中，L、R、O各区数量分别为5、3和20。以顺序规划和随机遍历2种方法作为对比。

试验结果如表4所示，对于试验1，本文方法相比于顺序规划法和随机遍历法，路径总长度分别减少47.5%和51.16%，遍历总时长分别减少10.69%和27.18%。当果实为布局2时，果实分布相对集中于重叠采摘区，3种方案的路径总长度均有所下降，本文方法未发生访问冲突，而另外的2种方法和均出现不同程度的访问冲突，增加了遍历时长，本算法较顺序规划法和随机遍历法时长减少了20.45%和23.33%。随着果实进一步集中，当果实为布局3时，3者遍历总长度均显著减少，但访问冲突情况增加，排队等候时间对遍历总时长的影响最为显著，本文方法的异步访问优化机制效果明显，有效降低了冲突次数，缩短了遍历总时长，相较于顺序规划法和随机遍历法，遍历时长分别减少12.94%和21.69%。

表4 不同果实分布下双臂协同采摘机器人采摘试验结果 Table 4 The experimental results of dual-manipulator robotic harvester under different distribution of fruits

综上，果实分布均匀稀疏情况下，遍历路径总长度对总作业时间影响较为明显，优化多机械臂的采摘遍历路径长度可有效提升效率；果实分布较为密集情况下，仅优化遍历路径长度对效率的提升不大，访问冲突引起的排队等候占主导地位，异步访问协调机制作用明显。本文任务规划方案以遍历总时间为优化目标，考虑访问冲突和遍历路径长度对总时长的影响，不同的果实分布条件下，均可提升采摘效率。

4 结论

1）本文将矮化密植果园多机械臂机器人采摘任务规划归纳为异步重叠访问域多旅行商问题，基于遗传算法给出了问题的求解方法。仿真试验结果表明：所提方法求解不同重叠访问域多旅行商问题时，可分别在500、2000和2500次迭代后收敛至满意解，具有良好的收敛性。

2）针对多个机械臂访问重叠区内果实发生冲突的问题，本文方法引入异步规则，对不满足异步规则的任务规划方案施加惩罚，以总遍历时长为优化目标，确保重叠访问域内多臂异步协同；仿真算例表明，本文方法相比于随机遍历方法，在43颗果实条件下遍历时长可缩短40.97%，在90颗果实条件下分别最多可缩短54.98%；单臂采摘90颗果实的遍历时长约为本文算法4.28倍。

3）在实验室环境下，设置了3种不同情况的果实分布，开展2个机械臂的协同采摘试验，结果表明，本文在3种果实分布情况下，相较于顺序规划法和随机遍历法，本文方法的作业遍历时长分别缩短10.69%和27.18%、20.45%和23.33%以及12.94%和21.69%。