基于超声波测量油膜厚度方法的研究
2021-04-01姚志伟魏永庚
姚志伟,魏永庚,石 勇
(黑龙江大学 机电工程学院,哈尔滨 150080)
0 引 言
机械部件运动一般采用润滑油减少摩擦发热和损耗,油膜厚度过大或过小都可能引起机器的故障。测量零部件间隙中油膜厚度对减少机械运动摩擦发热、保证机器正常运转有着非常大的经济价值。目前测量油膜厚度的方法很多,超声波测量技术采用非侵入测量方法,更加方便快捷,有着更好的技术优势和发展前景。
在国外, 2010年 Dwyer-Joyce R S在测量内燃机衬套中往复运动的活塞的润滑油膜厚度时,使用了反射超声波对油膜厚度进行无创测量的方法[1]。2011年Gasni D等基于超声反射技术在等粘度弹性润滑条件下测量了润滑膜的厚度[2]。2012年,Ibrahim M K W等使用超声波反射方法,通过实验测量了滚动轴承中外圈与滚珠之间的膜厚分布[3]。2019年, Al-Aufi Y A等用超声技术对垂直管道中的波浪状液体薄膜厚度进行了测量[4]。2020年Beamish S等采用了超声波振幅、相变和共振倾角技术获得了定制轴颈轴承测试平台中的周向膜厚度分布[5]。与此同时,Kanja J等使用反射的超声波脉冲来测量固体背面的涂层厚度[6]。
在国内,2005年卞伟等对超声波水浸聚焦检测焦距的特性进行了探讨[7]。2010年唐伟坤等提出利用反射系数测量油膜厚度的方法,并建立反射系数法的连续模型和弹簧模型[8]。2014年申洪苗等根据垂直入射超声波在3层介质中传播的相关理论,对给定油膜厚度的试件进行了超声测量[9]。同年,杨晓对超声波油膜厚度测量方法及测量系统进行了研究[10]。2015年皮光玉通过建立水-钢-水的三层介质模型,探讨了共振频率处超声波的透射和反射特性[11]。2016年Zhang K等使用压电元件替代传统的超声波换能器,并测试了使用压电元件的油膜厚度测量的准确性[12]。2017年章何菁等对超声油膜厚度测量的研究现状做了全面的综述[13]。2020年Dou P等基于超声技术提出了一种用于全范围测量的统一时域模型来测量封闭轴承的摩擦副中油膜厚度[14]。与此同时,Yu M等提出 同时利用复数超声反射系数的幅度和相位,并通过数学方法得出油膜厚度[15]。
国内外很多研究学者对超声波测量油膜厚度做了一定的研究,但对于基于超声波脉冲反射信号来具体分析测量油膜厚度方法的研究还比较少。对于超声波脉冲反射信号测量油膜厚度开展了进一步的试验与研究,并为测量其他零部件间的油膜厚度奠定了基础。
1 建立模型理论
声波在传播到不同介质分界面时会发生反射和透射,机械部件间形成的润滑油膜相当于两固体介质之间的液体夹层。超声波入射到固体表面时会发生部分能量的反射,另一部分被透射;超声波在固体与液体界面时也发生反射与透射。若忽略能量的损耗,能量的反射可以用反射率R来表示:
(1)
式中:Z1、Z2分别为边界两侧介质的特性阻抗,Z=ρc;ρ为介质的密度;c为声波在介质中传播的速度。
1.1 谐振模型理论
超声波入射到第一层介质表面时,部分超声波发生反射,另一部分超声波透射过去,在第一层介质与液体界面处,超声波发生第二次反射,如果液体厚度很小且与超声波波长一致时,采用谐振模型计算液体的厚度。根据超声波在结构中测量液膜厚度的情况,建立超声波在3层介质中传播的理论模型,见图1,At和Ar分别是入射波和反射波。
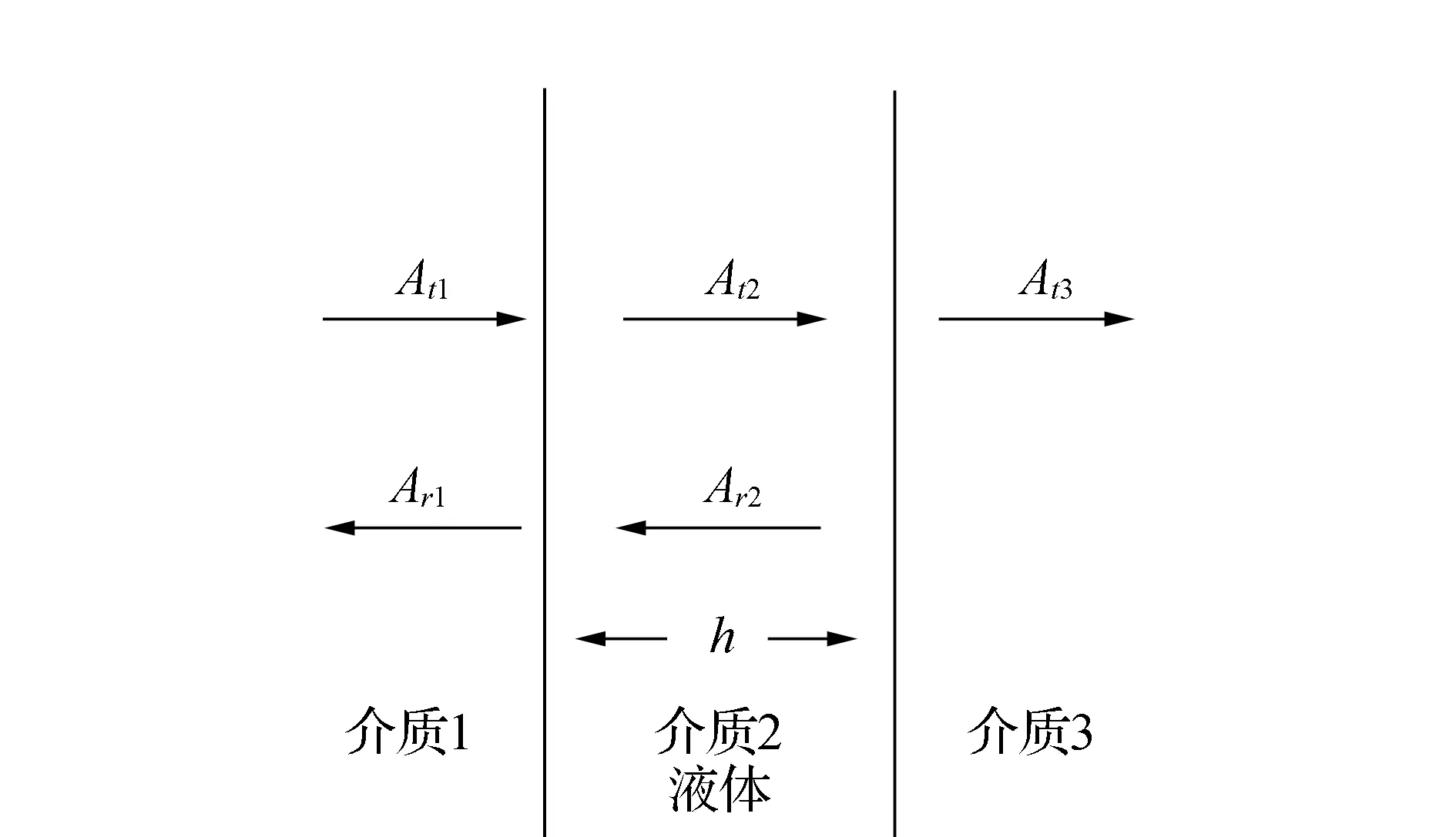
图1 超声波在3层介质中传播的理论模型Fig.1 Theoretical model of ultrasonic propagation in three-layer medium
根据谐振频率定义可知液体油膜厚度h表达式为
(2)
式中:c为超声波在液体夹层中的传播速度;m为谐振的阶数;f为m阶谐振频率。
对于金属-液体-金属3层介质结构,根据界面1-2和2-3上连续应力和位移的边界条件,反射系数R表达式如下
(3)

若w为谐振频率,则s2=0,式(3)表示为
(4)
若介质一与介质三为同一种介质时,即Z1=Z3,此时反射系数R=0。
通过式(3)并采用不锈钢-油-不锈钢结构,使用MATLAB软件得到超声波反射系数与入射频率之间的关系曲线。通过给定不同油膜厚度:60、80、100和120 μm,可以得到不同入射频率与反射系数的关系,见图2。当反射系数在极小值点0时,所对应的频率即为谐振频率。
1.2 弹簧模型理论
当中间液体介质的厚度相对于超声波脉冲的波长非常小时,可以将中间液体介质看作一个反射层,超声波在边界的反射率可以用液体层等效弹簧的刚度来计算:
(5)
式中:R为反射率;w为超声波的角频率;k为液体层刚度系数。
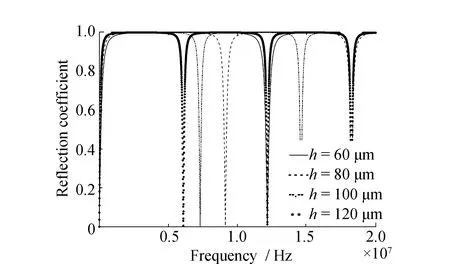
图2 不锈钢-油-不锈钢3层介质的超声波反射系数和入射频率关系曲线Fig.2 Relationship between ultrasonic reflection coefficient and incident frequency of stainless steel-oil-stainless steel three-layer medium
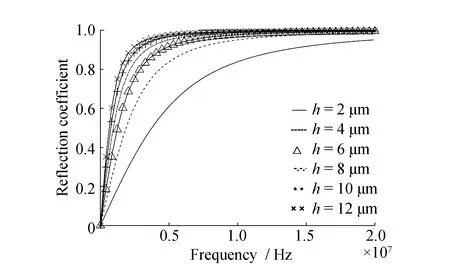
图3 不锈钢-油-不锈钢3层介质的超声波反射系数和入射频率关系曲线Fig.3 Relationship between ultrasonic reflection coefficient and incident frequency of stainless steel-oil-stainless steel three-layer medium
液体层的刚度系数为
(6)
由式(5)和式(6)得到液体层的厚度与反射系数之间的关系:
(7)
由式(7)可得,液体层介质不同厚度理论反射系数与频率的关系曲线,取h分别为2、4、6、8、10和12 μm时,超声波反射系数与入射频率的关系曲线见图3。
当油膜厚度与反射系数呈线性关系时,可求出油膜厚度:
(8)
式中:ρ为液体层介质的密度;c为液体层介质的声速。
若第一层介质与第三层介质相同时,即Z1=Z3=Z,式(8)可简化为
(9)
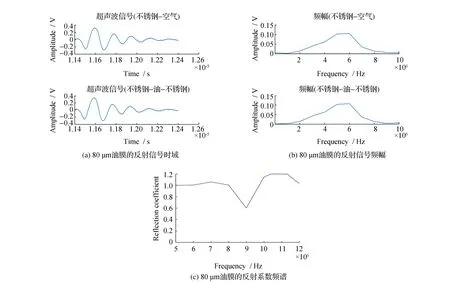
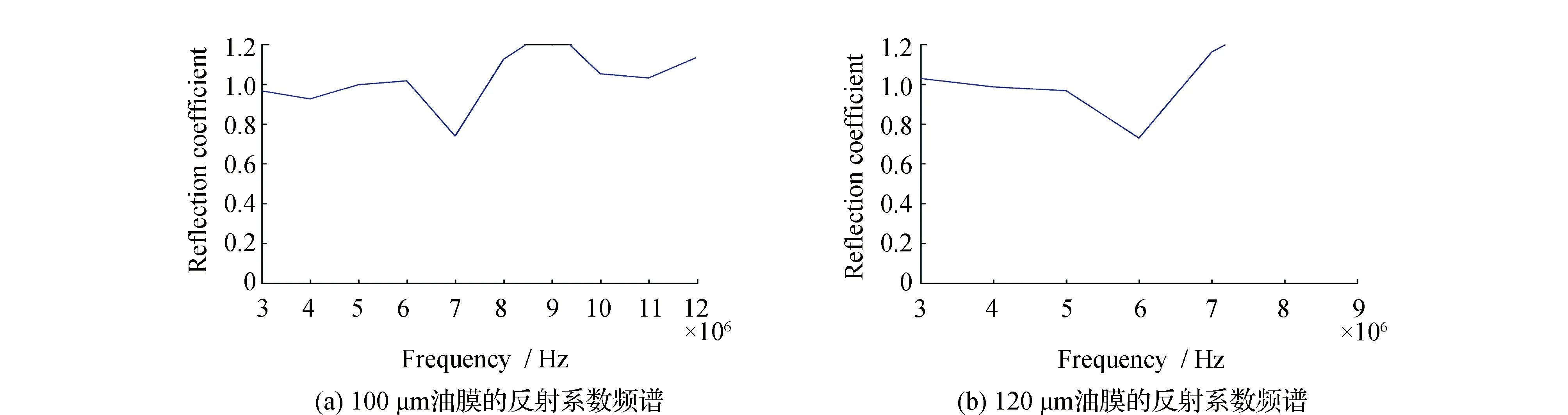
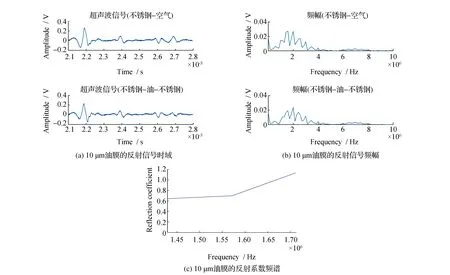
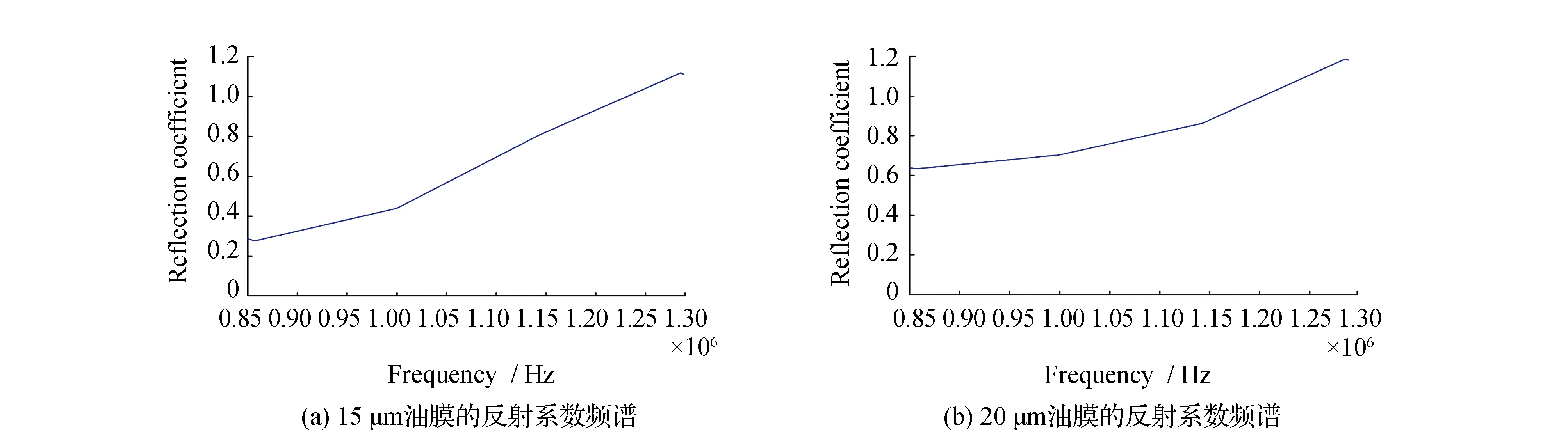
随着超声波脉冲入射频率增加,反射系数趋于1,不再有明显的变化,此时无法通过入射频率来计算油膜的厚度,见图3。为更准确测量油膜厚度,反射系数通常最佳测量范围为1.05×(Z1-Z2)/(Z1+Z2) 通常对于金属-液体假界面反射系数的测量一般采用间接计算的方式,通过已知的参考介质的反射系数Rr来间接求出反射系数R (10) 式中:Rr为金属-空气界面的反射系数为1;A(f)为超声波脉冲入射到金属-液体界面时反射波的幅值;Ar(f)为超声波脉冲入射到金属-空气界面时反射波的幅值。 试验装置包括数据处理的计算机、示波器、超声波脉冲收发器(UPR)、超声波换能器和油膜测量平台,在常温和标准大气压下进行实验,工作原理为:由UPR发出一定频率脉冲激励信号,经过超声波换能器将激励信号转换为一定带宽频率的超声波信号入射到油膜测量平台,由换能器接收超声波反射信号,并由UPR将反射信号发送至示波器和计算机。油膜测量平台分别采用柱形油膜测厚机构和楔形油膜测厚机构,并与之相对应的采用谐振模型与弹簧模型计算油膜厚度,试验装置见图4。 图4 试验装置Fig.4 Test device 2.1.1 柱形油膜测厚机构 柱形油膜测厚装置采用千分尺结构,测量原理是通过调节千分尺来测量油膜的厚度,可实现测量多个不同厚度油膜的目的,见图5。该装置最大分辨率为10 μm,不能测量小于10 μm的油膜厚度,只能采用谐振模型来测量油膜的厚度。 2.1.2 楔形油膜测厚机构 楔形油膜测厚装置采用楔形机构,楔形结构具有较宽的厚度调节范围,且分辨率比立式结构高得多,可以测得几微米的油膜厚度,测量原理是通过移动超声波换能器的位置,从而实现测量不同油膜厚度的目的,还可以通过更换不同厚度的塞尺来调节可测油膜的厚度范围,见图5、图6。 图5 立式油膜测厚装置Fig.5 Vertical oil film thickness measuring device 图6 卧式油膜测厚装置Fig.6 Horizontal oil film thickness measuring device 2.2.1 谐振模型测量油膜厚度 在立式油膜测厚机构测量试验中,采用不锈钢-油-不锈钢3层介质结构,进行测量了油膜厚度为80 、100和120 μm的试验,见图7。 图7 3层介质结构的超声波反射信号Fig.7 Ultrasonic reflection signal of three-layer structure medium 80 μm油膜超声波脉冲信号入射到不锈钢-空气表面和不锈钢-油-不锈钢3层介质表面时,换能器所接收的反射信号见图7(a);80 μm油膜的超声波反射信号进行快速傅里叶变换后的图像,即不锈钢-空气界面和不锈钢-油界面反射信号的超声波入射频率与对应幅值的关系图,见图7(b)。80 μm油膜的反射系数频谱见图7(c)。由图7(c)可见,反射系数是图7(b)中不锈钢-油-不锈钢3层介质反射信号的幅值与对应不锈钢-空气界面反射信号的幅值的比值。按同样的方法可以测得100 μm和120 μm油膜的反射系数频谱图,见图8。 图8 不锈钢-油-不锈钢结构的超声波反射信号Fig.8 Ultrasonic reflection signal of stainless steel-oil-stainless steel structure 由式(3)可知,图像中的极值点对应的频率即为测量液体油膜的谐振频率,将谐振频率fm带入式(2)即可求得油膜厚度h。多次测量取平均值分别测得80、100和120 μm油膜的厚度,测量值接近真实值,相对误差均小于5%,在允许范围内,测量结果见表1。 表1 立式结构油膜厚度测量结果Table 1 Oil film thickness measurement results of vertical structure 2.2.2 弹簧模型测量油膜厚度 在楔形油膜测厚机构测量试验中,采用不锈钢-油-不锈钢3层介质结构,进行测量了油膜厚度为10 、15和20 μm的实验,见图9。 10 μm油膜超声波脉冲信号入射到不锈钢-空气表面和不锈钢-油-不锈钢3层介质表面时,换能器所接收到的反射信号见图9(a)。10 μm油膜的超声波反射信号进行快速傅里叶变换后的图像,即不锈钢-空气界面和不锈钢-油界面反射信号的超声波入射频率与对应幅值的关系见图9(b);10 μm油膜的反射系数频谱见图9(c)。由图9(c)可见,反射系数是图9(b)中不锈钢-油-不锈钢3层介质反射信号的幅值与对应不锈钢-空气界面反射信号的幅值的比值。测得15 μm和20 μm油膜的反射系数频谱,见图10(a)和(b)。 由式(9)可知,取上图合适的反射系数和对应的频率值代入式(9)可计算得出测量油膜的厚度h。多次测量取平均值分别测得10、15和20 μm油膜的厚度,测量值接近真实值,相对误差均小于5%,在允许范围内,测量结果见表2。 表2 卧式结构油膜厚度测量结果Table 2 Oil film thickness measurement results of horizontal structure 图9 三层介质结构的超声波反射信号Fig.9 Ultrasonic reflection signal of three-layer medium structure 图10 不锈钢-油-不锈钢结构的超声波脉冲反射系数Fig.10 Ultrasonic pulse reflection coefficient of stainless steel-oil-stainless steel structure 通过对柱形测厚机构和楔形测厚机构的试验以及使用谐振模型和弹簧模型计算油膜厚度可知,在试验的过程中存在着诸多影响试验结果的因素,如温度、压强、实验器材本身的精度及误差等,通过这两种模型试验可得到以下结论: 1)两种模型试验中,在一定范围内随着测量油膜厚度的减小,计算油膜厚度所需入射频率随之增大。谐振模型试验中,测量油膜的厚度越小,对应谐振频率越高。在弹簧模型试验中,测量的油膜厚度一定时,在一定范围内超声波入射频率与油膜反射系数成一定比例关系,当入射频率超出一定范围时,油膜反射系数逐渐趋于1并不再与入射频率存在比例关系。 2)两种试验模型都有一定的测量范围,在20 μm以下的油膜厚度适用于弹簧模型,大于20 μm的油膜厚度通常适用于谐振模型。但两种试验模型之间并没有绝对的界限,两者之间还存在着测量盲区。 3)此次油膜厚度测量试验相比其他测量油膜的试验,同时采用了两种理论模型并对试验结果进行验证,并详细的分析了两种理论模型的特性。 4)两种模型试验对其他零部件油膜厚度的测量提供了一种新的途径,即非侵入式测量油膜厚度,对无损检测油膜厚度具有重要的意义。 5)试验中还存在其他的因素对实验结果产生很大的影响,如温度、压强、实验器材本身的精度等,在后续的试验中将会对温度这一影响因素进行更细致的研究。1.3 中间介质的反射系数
2 超声波测量油膜厚度

2.1 试验装置的组成

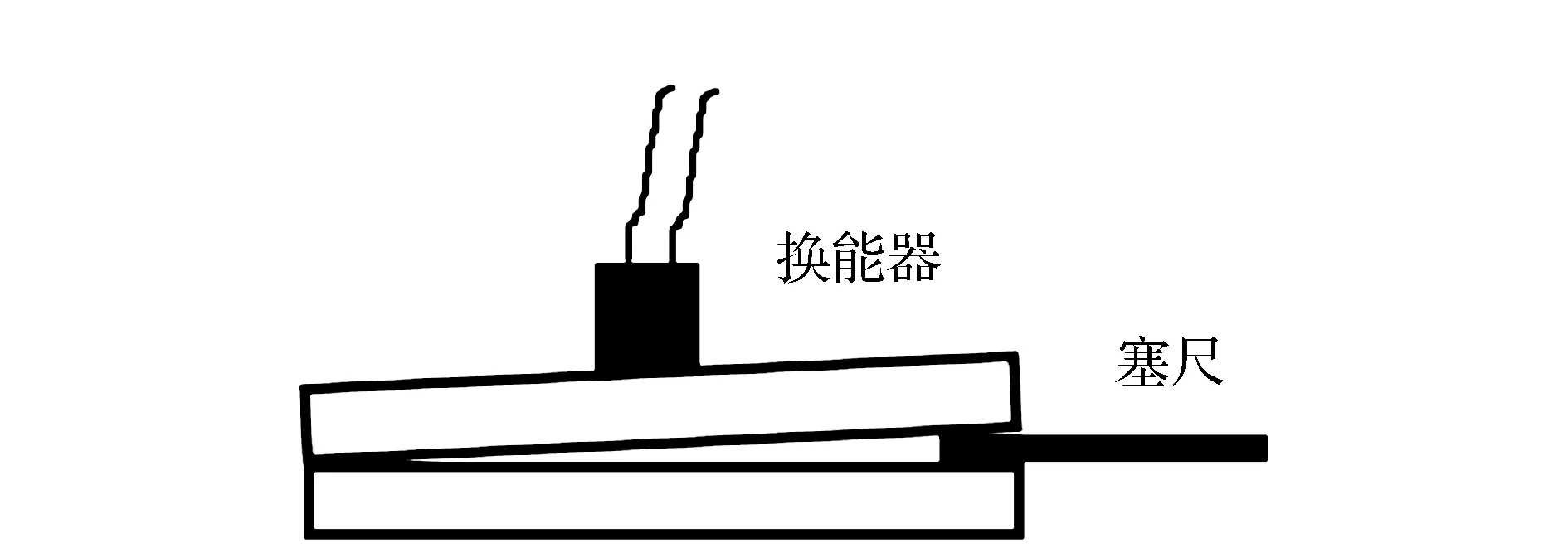
2.2 测量油膜厚度


3 结 论
