重金属在土壤-地下水中的迁移模型研究——以山西、陕西黄土高原塬区为例

张天玑，王海芳

(中北大学 环境与安全工程学院，山西 太原 030051)

0 引 言

根据《2019中国生态环境状况公报》显示，全国2 830处浅层地下水水质监测井中，Ⅰ～Ⅲ类水质监测井占23.7%，Ⅳ类占30.0%，Ⅴ类占46.2%，可见我国地下水质状况较差，地下水污染问题已成为人们关注的焦点问题[1].

重金属在降雨等因素作用下会迁移至地下水，地下水作为人类的主要水源之一，在饮用含有重金属的地下水后会直接影响人体健康，严重时会造成人体患病[2].地下水环境一旦受到污染，很难使其恢复至原来的状态[3].所以，研究重金属在土壤非饱和带的迁移转化，预测污染物进入地下水的浓度具有重要的理论与现实意义[4].现阶段研究人员解决环境污染问题的一个重要技术方法是将所研究的环境系统行为抽象为一个数学模型，这是进行定量研究工作的基础[5].

黄土高原塬区土壤表面重金属向地下水的迁移中，降雨的入渗水分对土壤重金属淋失具有显著影响[6].国内外已经研究出很多降雨入渗模型，如Green-Ampt、Smith-Parlange、Horton、Kostiakov模型等[7].Kostiakov模型计算简单，能够有效描述短期范围的降雨入渗过程.方正三[8]对Kostiakov公式和Horton公式进行了修正，用于研究在暴雨条件下黄土高原地区土壤渗透与时间的关系.研究土壤包气带污染问题的主要模型包括经验模型[9-10]、对流-弥散模型[11-14]和随机模型[15-16].其中，对流弥散方程是最常用、最基本的描述溶质运移的数学模型[17].Sun等[18]对 4种土壤进行了小土柱渗透试验和溶析仪实验，以对流-扩散方程为基础建立了锑在土壤中的迁移模型，对流-弥散模型可以解释锑在土壤中的迁移过程.对污染物迁移至地下水的研究方面，钟茂生等[19]采用三相平衡模型和SESOIL模型耦合地下水稀释模型对北京市不同水文地质条件下的 69种有机污染物和农药推导了基于保护地下水的土壤通用筛选值.基于此，本文将入渗模型、对流-弥散模型和地下水稀释模型进行耦合，描述污染物基于降雨入渗条件向地下水的迁移过程.最后利用MATLAB编程对该模型进行了验证.

1 重金属污染物在土壤中运移的影响因素

重金属污染物易溶于水，土壤中的微生物很难将其降解，重金属污染物一旦进入土壤就会发生持久性的污染.重金属在土壤中的迁移会受到自身理化性质，土壤对流、扩散和弥散作用，土壤质地，土壤水分等因素的影响.土壤质地的粘土含量越高，土壤中存在的自由水分含量和土壤空隙都会相应降低，重金属在土壤中运移就会受到限制[20]；而土壤含水量越高，对流和扩散作用就越大.对于黄土高原地区，降雨量少，土壤表面蒸发量大，重金属进入土壤后的迁移主要受降雨入渗水分的影响[21].

2 塬区水文地质条件

黄土高原塬区含水层岩性为离石组粉土质黄土中夹带有多层古土壤及钙质结核层，结构疏松且空隙、裂隙发育，其下部三门组粉质粘土，结构相对较密实，空隙、裂隙不甚发育，构成黄土塬区的隔水底板[22].

黄土高原塬区潜水主要分布在较大的黄土塬体中，在塬面宽度大于400 m时均存在潜水，深度一般在50 m～80 m.

黄土高原塬区潜水补给的最主要来源为大气降水.黄土塬区宽阔有利于降雨下渗，黄土颗粒细密.野外渗水试验显示黄土的垂直渗透系数为2.1 m/d～7.8 m/d，透水性较好[22].

3 降雨入渗条件下污染物运移模型的构建

3.1 概念模型

黄土高原地区降雨稀少，降雨多集中在每年的夏季，蒸发强烈，研究区土壤表面到潜水面的厚度为H，土壤中污染物向下迁移主要依靠降雨入渗的垂向迁移，存在的微弱侧向流动可忽略，故可将非饱和带概化为垂向一维流.假设土壤包气带是均质各向同性的，污染物运移模型为对流-弥散方程，模型上边界设定为定浓度边界，下边界设定为零浓度边界.

污染物迁移模型见图1.

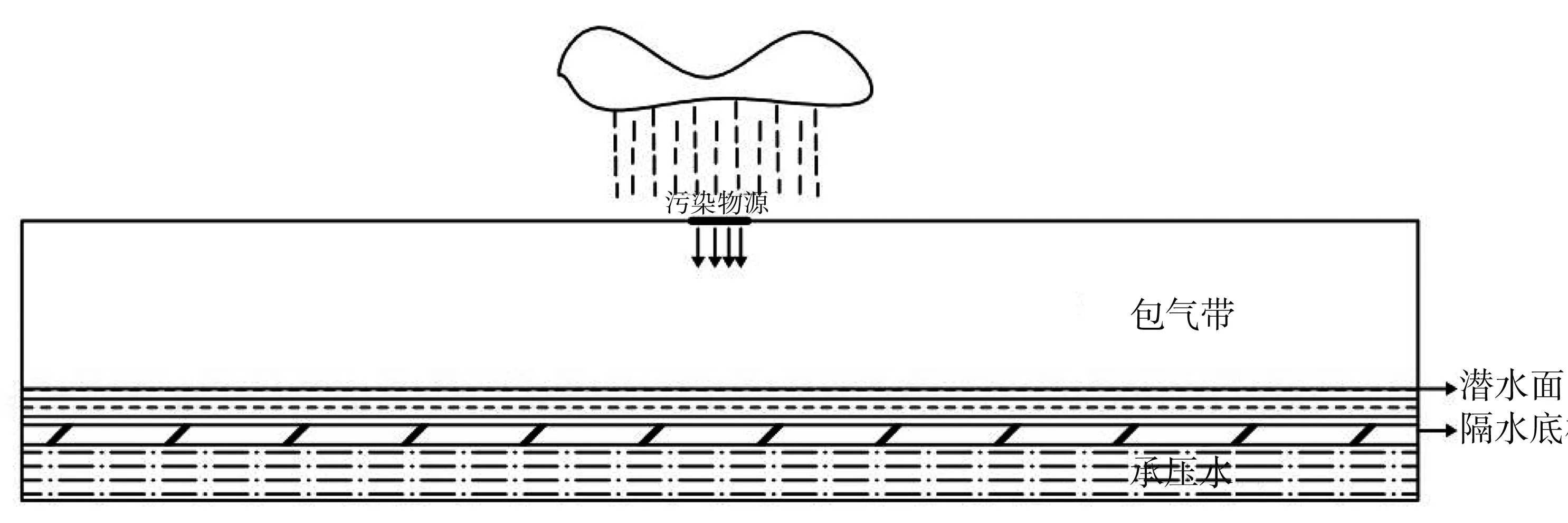
图1 研究区污染物迁移概念模型图

3.2 降雨入渗模型

在降雨条件下的降雨入渗量采取Kostiakov 三参数入渗经验模型，该模型是很多国家地区使用的入渗模型，研究比较成熟且入渗参数的物理意义明确[23]，模型如下

I(t)=ξtα+Kst，

(1)

式中：I(t)为t时刻的累积入渗量，cm；ξ为入渗系数，表示入渗开始后第一个单位时间末扣除Ks后的累积入渗量，cm；α为入渗指数，表示土壤入渗速度的衰减速度；Ks为土壤相对稳定入渗率，也称为饱和导水率[24-25]，是在单位土壤势梯度下饱和土壤的入渗速度或非饱和土壤入渗达到相对稳定阶段的入渗速度，cm/min.

降雨入渗条件下，由降雨强度及根系吸附作用得到的土壤包气带空隙水实际平均流速v为[26]

(2)

式中：ξ为降雨入渗系数；Jw为降雨入渗速度；CET为植物蒸腾系数；θ为包气带平均体积含水率；q为包气带渗流速度.

由于黄土高原地区干旱少雨，植被稀少，忽略植被蒸腾作用，省去由于植物蒸腾作用消耗的水量项，将式(1)代入式(2)得

(3)

由于黄土高原塬区土壤地下水补给主要为大气降雨，污染物进入表土层后，随着降雨入渗的土壤水分向地下迁移.由于各地区土壤质地不同，降雨入渗量也不相同，从美国EPA获取到各种土壤质地的饱和导水率值，见表1，根据研究区土壤质地条件即可知研究区土壤饱和导水率，利用式(2)可求得土壤孔隙水流速.

表1 土壤质地对应的饱和导水率值

3.3 污染物在土壤非饱和带迁移模型

3.3.1 模型推导过程

污染物在土壤中的运移主要考虑对流、分子扩散和机械弥散3个物理过程以及土壤对污染物的吸附作用.

对流引起的溶质通量与土壤水流通量和水中溶质浓度有关，溶质对流通量可表示为

Jc=qC,

(4)

式中：Jc为溶质的对流通量，mol·m-2·s-1；q为水通量，m/s；C为单位体积土壤水中溶质的量，mol/m3、kg/m3或g/L，即溶质浓度.

由于土壤水流通量可表示为

q=vθ，

(5)

所以，式(4)可写

Jc=vθC,

(6)

式中：v为平均空隙流速，m/s；θ为土壤体积含水量，m3/m3.

由于机械弥散和扩散在土壤中会引起溶质浓度的混合和分散，且微观流速不易测定，弥散和扩散结果不易区分，所以，将两者联合作为水动力弥散.用菲克第一定律表示的扩散作用为

(7)

式中：Js为溶质的扩散通量，mol·m-2·s-1或kg·m-2·s-1；Ds为溶质的有效扩散系数，m2/s；dC/dx为浓度梯度.土壤溶质扩散可表示为

(8)

式中：Ds为扩散系数.

机械弥散为

(9)

式中：Dh为机械弥散系数，m2/s.

将式(8)与式(9)联立可得到水动力弥散通量为

(10)

式中：D为水动力弥散系数.

污染物等溶质在进入水土环境后，土壤固液相快速发生吸附、解吸作用，在很短时间或瞬间就能达到平衡状态.假设土壤中所吸附的溶质量和土壤溶质浓度是线性关系，采用Henry吸附模型(线性吸附)表示土壤与污染物之间的吸附

S=KdC,

(11)

式中：S为单位土壤吸附污染物的量；Kd为污染物分配系数.

土壤溶质运移主要是对流和水动力弥散(机械弥散和扩散)作用的结果，联立式(4)和式(10)可得出溶质通量为

(12)

假设土壤三维空间内一单元六面体ABCD-EFGH(见图2)为一单位容积土壤体，其边长为Δx、Δy、Δz.在Δt时间内，污染物进出单元体的变化符合质量守恒原理，无源汇项存在，即进出该单元体的污染物的量的差等于Δt时段内该单元体内污染物质量的变化.

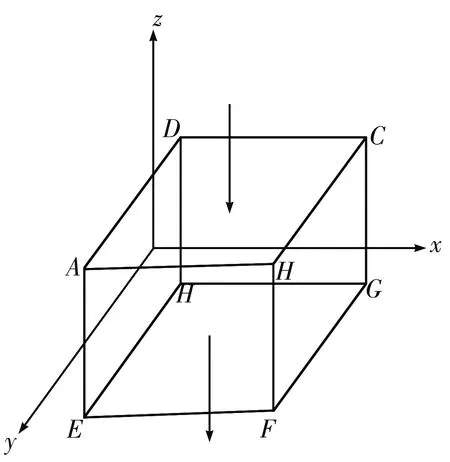
图2 污染物进入六面体单元示意图

设进入六面体上界面ABCD面溶质通量为Jx，则Δt时间内由上界面进入的污染物的量为

mx=JxΔyΔzΔt，

(13)

流出六面体下界面EFGH面的溶质通量为

(14)

Δt时间内流出下界面EFGH的溶质量为

(15)

在Δt时间内沿x轴方向的污染物流入与流出单元体的污染物质量差值为

(16)

同理，在Δt时间内，沿y轴和z轴方向的污染物流入与流出质量之差为

(17)

(18)

所以，在x，y，z3个方向上溶质流入量与流出量的总差量为

(19)

根据质量守恒定律，Δt时间内该单元体中溶质量的变化为流入与流出单元体中的溶质质量的差值，即为

(20)

将式(20)两边除以ΔxΔyΔzΔt得

(21)

利用爱因斯坦求和约定表示为

(22)

在一维条件下

(23)

将式(12)代入式(23)得一维条件下的对流弥散方程为

(24)

一维条件下考虑污染物在土壤的吸附交换项，则式(24)变为

(25)

将式(5)和式(11)代入式(25)，考虑对流、水动力弥散和吸附作用，污染物在黄土高原塬区土壤非饱和带中迁移的一维水动力-弥散方程为

(26)

式中：ρ为土壤质量密度；θ为土壤的体积含水率；C为土壤中污染物浓度；Dx为垂直方向上水动力弥散系数.

将阻滞因子引入方程，降雨因素以源汇项考虑，则式(26)变为

(27)

式中：Rd为阻滞因子；Q为降雨导致的源汇项.

3.3.2 模型边界条件及解析解

研究区污染源主要为连续或短期释放源，并且考虑降雨和污染物在土壤中的吸附，且输入浓度为一个常量，根据水文地质概念模型可将边界条件定为如下表示：

初始条件

C(x,t)|t=0=Ci,-∞≤x≤+∞；

(28)

边界条件

(29)

(30)

根据初始条件和边界条件，式(27)的解析解为

C(x,t)=

(31)

(32)

B(x,t)=

(33)

3.4 污染物进入饱和地下潜水模型

污染物随土壤水分进入潜水时，与地下潜水混合后被稀释，污染物浓度会随之降低.污染物进入地下水与地下水混合稀释后的浓度预测模型主要采用箱式模型来完成.

Cgw=Cp/DAF,

(34)

式中：Cgw为混合稀释后污染物的质量浓度，mg/L；Cp为污染物接触潜水面时的浓度，mg/L，通过对流-弥散方程进行确定；DAF为地下水稀释因子.

地下水稀释因子DAF也可以根据当地的地下水水文地质条件计算求得[27]，公式如下

(35)

D=(0.011 2×L2)1/2+

(36)

式中：K为含水层导水率，m/a；i为水力梯度，m/m；D为混合区深度(污染物与地下水混合的深度)，m；I为地下水渗透速率；L为污染源到监测点的水平距离；Hgw为含水层厚度.

4 模型的优势与对比分析

目前，对于重金属在非饱和-饱和土壤中迁移的整体性模型研究还不多.姜利国等[28]考虑了重金属在地下水中的对流、弥散、吸附以及微生物降解作用，在非饱和-动理论及溶质运移理论基础上建立了非饱和-饱和区域内水流方程与重金属污染物运移方程耦合的数学模型.李锡夔[29]提出了一个考虑了污染物运移的对流、机械逸散、分子弥散、吸附、蜕变、不动水效应的模拟饱和-非饱和土壤中污染物运移过程的数值模型.利用算例验证了在一二维条件下污染物的运移状况.刘培斌等[30]建立并验证了在排水条件下田间一维饱和-非饱和土壤中氮素运移与转化的耦合模型，模型中考虑了有机质的矿化、氮素的吸附、硝化、反硝化、氨气挥发及作物根系吸氮等氮素转化作用过程，同时也考虑了土壤温度和湿度对氮素转化的影响.Grift B V D等[31]研究出一种模型方法来评估污染物对地下水和地表水负荷的影响，耦合非饱和带淋溶模型和三维地下水运移模型，采用质量平衡方法对3个冶炼厂附近的3个不同集水区进行了污染物预测模拟.

依据以上论述，目前国内外在该方面的研究主要是实验室结合土柱实验或对厂区小范围内重金属在土壤-地下水中的迁移模型研究，无法推广使用.本文所建立的模型针对不同的暴露情景，选取黄土高原塬区为研究对象，将降雨入渗模型、对流弥散方程与地下水稀释模型进行耦合，该耦合模型充分考虑降雨、水文、地质及污染物特征等因素.在污染物进入土壤后用一维对流-弥散方程进行描述，给定具体的边界条件即可计算得到污染物迁移至潜水面的污染物浓度.污染物进入地下水后用地下水稀释模型描述，充分考虑研究区的水文地质条件，进而计算污染物与地下水混合稀释后的浓度.将土壤饱和导水率与土壤质地结合在一起确定饱和导水率.前人研究的模型的计算方法都比较复杂，考虑的因素太多不易操作，很少考虑水文地质及降雨等因素.

5 数学模型验证

假设土壤中污染物的环境背景值为零，地表除污染源以外无任何流体进入模拟区域.参考文献[32-34]，设置相应参数为：土壤质量密度ρ=1.6 g/cm3，土壤的体积含水率θ=0.4 cm3/cm3；垂直方向上水动力弥散系数Dx=400 cm2/d；土壤水平均孔隙流速v=20 cm/d；液相和吸附相间溶质分配系数为1.17 cm3/g；模拟深度为潜水埋深x=50 m；模拟时间为365 d.

初始条件与边界条件：

C(x,0)=0，x>0；

C(0,t)=8.96 mg/L, 0

C(0,t)=C(x,10),t≥10；

C(∞,t)=0,t>0.

利用MATLAB编程模拟污染源存在10 d时的重金属污染物运移过程，分别获得10 d，20 d，40 d时土壤中重金属污染物质量浓度分布及50 m深度处运移时间与重金属浓度之间的关系图，如图3～图6 所示.

图3 10 d时重金属与包气带深度的关系曲线

图4 20 d时重金属与包气带深度的关系曲线

图5 40 d时重金属与包气带深度的关系曲线

图6 50 m深度处重金属与运移时间的的关系曲线

从模拟结果看出，当污染源是瞬时污染源时，在释放重金属污染物阶段，重金属浓度分布随着距离的增加而减小，直至在空间分布上趋于稳定.这是因在靠近污染源处，污染源浓度较大，经过一段时间的弥散，浓度会逐渐减小，因弥散速度较小，在短时间内，重金属只能弥散很短距离，较深土壤中污染物浓度较少.当重金属污染源不存在后，重金属在土壤各深度处的分布先迅速增加然后减小，这是因为在没有新的污染源进入时，重金属浓度逐渐减小，重金属迁移过程中浓度梯度会越来越小，使某一点的重金属浓度有一个积累的过程，然后又进行释放，这与宋新山等[4]的研究基本吻合.

6 结 论

研究重金属在饱和-非饱和土壤中迁移的整体性模型不多，本研究将降雨入渗与重金属所在饱和非饱和土壤作为一个整体考虑，通过将入渗模型、对流-弥散模型和地下水稀释模型进行耦合，达到计算基于保护地下水的土壤风险值的目的.与前人研究的饱和-非饱和带迁移模型进行对比分析，本模型考虑了降雨以及当地水文地质条件，模型操作简单，普适性强.利用MATLAB软件编程对模型在给定初始条件及边界条件下进行了验证，与前人研究结果基本吻合，能够预测污染物在包气带的迁移规律以及重金属到达潜水面的浓度.本次分析只以我国黄土高原塬区为研究对象，后期研究应该对我国各个地区地下水进行污染调查，选择典型样地，并结合当地水文地质条件、气候条件、地下水类型和埋深条件建立场地暴露概念模型，为后期重金属的地下水质量评估提供理论支撑.