转台误差对MEMS陀螺标定的影响分析

李 登，张 鹏,2，李孟委,2

(1.中北大学 仪器与电子学院，山西 太原 030051；2.中北大学 南通智能光机电研究院，江苏 南通 226000)

0 引 言

惯性导航系统广泛应用于航空航天、制导武器等军用领域及汽车安全、消费电子等民用领域.MEMS陀螺是惯性导航系统进行测量的关键元件，提高其精度不仅可以提升导航系统性能，更对提高国防实力及人民生活水平具有重要意义[1].一般来说，提高MEMS陀螺精度的方法有两种：一是从仪表的研发角度提高其精度，研究新机理、新效应、新工艺，但往往投入很大，而产出较小；二是建立MEMS陀螺误差参数模型，编排合理的测试路径，利用高精度的测试设备如三轴转台，标定出误差模型中的参数，从而对MEMS陀螺进行补偿[2-3].MEMS陀螺标定就是通过转台的输入给MEMS陀螺一个稳定的角速率输入，然后采集MEMS陀螺的输出，经过数据处理估计出MEMS陀螺各项误差参数[4].事实上，由于测试设备三轴转台的不精确性和环境因素的影响，会使标定结果存在误差，如转台的轴线垂直度误差、倾角回转误差以及运动控制精度误差等都会影响标定时MEMS陀螺的输出，从而影响标定精度[5].

文献[6]为了提升陀螺的标定精度，采用正反转试验减小了地球自转对陀螺角速率的影响，但是没有定量和定性分析这种影响的程度和大小.文献[7]分析了速度误差与惯性测量单元误差间的关系，建立了IMU系统级标定模型，主要抑制陀螺和加速度计的噪声影响.文献[8]提出了一种自适应零速修正方法，采用基于普条件数可观测理论对系统各状态进行可观测性分析，实现了对位置、姿态、速度等误差的估计，从而提高精度.但对于转台的几何指标，如倾角回转误差和垂直度误差等并没有做相关的定量及定性分析.

本文采用多体系统误差建模理论，考虑实际转台运动中带来的倾角回转误差、垂直度误差等影响，建立三轴转台误差模型，阐述陀螺标定原理，通过理论分析得到有转台误差项时的陀螺全参数误差模型和没有转台误差项的陀螺误差模型，通过速率标定实验，分别得到两种情况下标定的陀螺误差参数项，经过做差验证了转台误差对陀螺误差参数的影响.

1 转台误差建模

1.1 多体系统误差建模理论

在实际工程中，常常有多个刚体连接成的复杂机械系统，可以把他们归结为多体系统，因此，可将三轴转台看成多体系统.在多体系统理论建模过程中，常常考虑与系统运动精度有影响的各类因素和各种耦合情况，解决复杂机械系统的运动问题，建立的约束条件较少，建模过程比较规范[9].

1.2 基于多体系统理论的转台误差模型

图1 所示为本次采用的三轴转台模型，理想情况下，外框轴线始终与地面垂直，3个轴轴线相互垂直，而实际上，由于受加工装配、制造精度、运动控制以及环境等因素影响，三轴转台往往存在各类误差.转台旋转时，3个轴产生的运动误差可以用轴系回转误差来表示，轴线垂直度由于转台框架运动特点常被转变为轴间的垂直度以及轴线之间的轴线相交度.

图1 实验所用转台结构

设地理坐标系为0体，定义低序列算子如图2 所示，将基座标为1体，外框轴系标为2体，中框轴系标为3体，内框轴系标为4体，在内框轴坐标系下直接安装MEMS陀螺.对得到的三轴转台低序体阵列进行坐标变换，可以得到任意两个个体间的运动和位置关系.

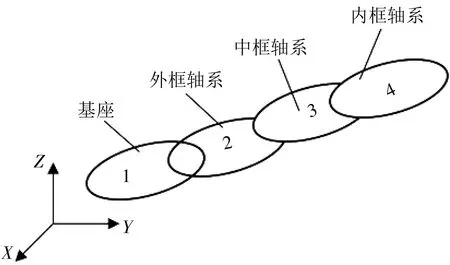
图2 三轴转台低序体阵列

根据图3 中两体间运动误差分析示意图，某点的位置矩阵可以用以下公式在地理坐标系中表示

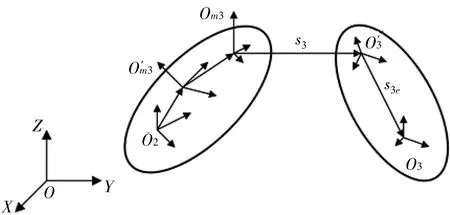
图3 两体间运动误差分析

(1)

2 三轴转台误差分析

2.1 转台几何误差分析

2.1.1 倾角回转误差

在转台运动中，对标定设备影响较大的是各个轴系的晃动与偏差，因此，对倾角回转误差进行规定.三轴转台运行时，任意时刻的轴系主轴包含两个运动，一是绕自身回转轴线旋转；二是自身回转轴线和主轴对于转轴平均轴线有轴向、径向和倾角的运动[10-13].

2.1.2 垂直度误差

将两轴线间角度与90°的差值定义为垂直度误差.转台的指向精度主要受轴线垂直度的影响，所以，验收转台时会对轴线垂直度提出很高的要求.转台在实际运行时，各个轴间运动会产生轴间耦合，轴线间的瞬时回转轴线垂直度与平均回转轴线垂直度以及两轴的角位置都有关系，但在本文中忽略其相互影响.

2.1.3 角位置误差

角位置误差是指理论上转过角度与实际转过角度的差值，由于本文采用单轴速率双轴位置法进行试验，选取外框轴做速率，其角位置误差对标定没有影响，主要受其他两轴的谐波分量的影响.

2.1.4 MEMS陀螺对准误差

MEMS陀螺对准误差是指陀螺的各旋转轴与系统定义的参考系之间的角度差，陀螺对准误差主要与加工工艺和安装不正交度有关.

2.2 各坐标系设置

在三轴转台建立地理坐标系o0x0y0z0，外框轴坐标系o1x1y1z1，中框轴坐标系o2x2y2z2，内框轴坐标系o3x3y3z3和MEMS陀螺坐标系OXYI，其中X表示MEMS陀螺的x轴方向，Y表示MEMS陀螺的y轴方向，I表示MEMS陀螺的输入轴方向[14].在理想状态下，三轴坐标系是重合的，转动角度为零，在内框轴坐标系上安装MEMS陀螺.初始时刻，MEMS陀螺的x轴与中框轴平行，y轴与内框轴平行，输入轴I与外框轴平行，如图4 所示.

图4 坐标系示意图

2.3 各坐标系间姿态矩阵推导

2.3.1 低序体1基座相对于地理坐标系的姿态矩阵

外框轴线与地面垂直，因此，低序体阵列1基座主要考虑外框轴线的各项误差，基座外框轴的零位误差为Δφz1；轴线垂直度误差为Δφx0和Δφy0；外框轴倾角回转误差为Δθx1(α)和Δθy1(α)，是与外框轴转动角度α相关的函数，将倾角回转误差展开成傅里叶级数，取二次谐波为主要部分，用公式表示

(2)

式中：Δθx1c, Δθx1s, Δθy1c, Δθy1s为倾角回转误差二次谐波的正弦项和余弦项的幅值.因此，低序体1基座相对于地理坐标系的姿态变换矩阵可表示为

Rot(x0,Δφx0)Rot(y0,Δφy0)Rot(x0,Δθx1(α))×

Rot(y0,Δθy1(α))Rot(z0,α)Rot(z1,Δφz1),

(3)

式中：Rot(i,θ)为绕i轴旋转θ角所形成的姿态变换矩阵，其中

(4)

2.3.2 低序体2外框相对于低序体1基座的姿态矩阵

中框轴的零位误差为Δφx2，外框轴线与中框轴线间垂直度误差为Δφy1，中框轴线的倾角回转误差Δθz2(β)和Δθy2(β)为中框轴线角位置β的函数，表示为

(5)

低序体2外框相对于低序体1基座的姿态矩阵为

Rot(z1,Δθz2(β))Rot(x1,β+Δβ)×

Rot(x2,Δφx2).

(6)

2.3.3 低序体3内框相对于低序体2中框的姿态矩阵

Δφz2为中框轴轴线与内框轴轴线的垂直度误差，内框轴的倾角回转误差Δθz3(γ)和Δθx3(γ)是内框轴线角位置γ的函数，可以表示为

(7)

低序体3内框相对于低序体2中框的姿态矩阵可表示为

Rot(z2,Δθz3(γ))Rot(y2,γ+Δγ).

(8)

2.3.4 MEMS陀螺相对于低序体3内框的姿态矩阵

MEMS陀螺的初始对准零位误差为Δφz3，相对于内框轴系的安装误差为Δφzx3和Δφzy3.考虑MEMS陀螺直接安装在内框基面上，因此，MEMS陀螺相对于低序体3内框坐标系的姿态矩阵为

(9)

2.3.5 角位置误差

3个轴系存在角位置误差Δα、Δβ、Δγ，其中Δα对标定没有影响，Δβ和Δγ有一次谐波、二次谐波部分，故有

(10)

3 陀螺标定原理及误差模型建立

3.1 陀螺标定原理

在陀螺标定时，当转台角速率很大时，转动时间较短，而地球自转角速率远远大于MEMS陀螺的漂移量，所以，陀螺的漂移和标度因数矩阵可以分开标定.常用的方法是将陀螺安装在转台内框上，控制转台的3个轴进行正反转动各n圈，设定单位时间，采集陀螺角速率输出，用陀螺正转的输出脉冲与陀螺反转的输出脉冲做差，削弱地球自转角速率以及陀螺自身漂移的影响.标定使用的转台为三轴转台，台体形状为U-O-O型，三轴可连续360°旋转.MEMS陀螺安装在内框，按照图4 所示进行安装，标定时外框连续转动，通过控制中框和内框使标定轴依次和外框轴重合[15].

具体标定流程如下：首先对转台进行通电预热，与之连接的陀螺在运行一定时间后，待陀螺输出数据平稳后，设定单位采样时间，本次标定的编排路径为单轴速率双轴位置法进行参数标定，转台的外框作为输入轴，输入恒定的角速率，内框轴和中框轴处于角位置状态，记录外框角速率以及内框角位置和中框角位置，并进行正反旋转两次实验，以抵消地球自转和陀螺自身漂移带来的影响.

3.2 MEMS陀螺误差模型建立

为了更好地辨识出MEMS陀螺误差参数，不只需要获得零偏及标度因数等常规参数，因此采用以下模型

y=K0+Kxωx+Kyωy+KIωI+Kxyωxωy+

(11)

式中：K0为零偏；Kx、Ky、KI为x轴、y轴、输入轴的比例系数；ωx、ωy、ωI为x轴、y轴、输入轴的角速率；Kxy、KIx、KIy为耦合系数；Kxx、Kyy、KII为二次项比例系数；ε为残差.

MEMS陀螺角速率沿外框轴输入的分量为

(12)

将式(6)、式(8)、式(9)代入式(12)后，得到

(13)

针对x轴和y轴的角速度分量，由于与其相乘的误差系数是极小量，因此只写出标称值.外框轴上的角速度代入全部误差参数，将式(13)代入式(11)后，得

(14)

由此得到MEMS陀螺输出在忽略地磁影响下的全误差方程，可以看出三轴转台由于存在各项误差，对MEMS陀螺的输出也带来偏差，由此标定出来的系数也会产生偏差，因此，想要精确标定MEMS陀螺的误差系数，需要对转台各项误差进行测量，得到相应误差系数值，代入陀螺全误差参数模型中，提高标定精度.

在不考虑转台误差时，MEMS陀螺输出公式为

(15)

4 实验验证

对MEMS陀螺进行速率位置标定实验，按照MEMS陀螺标定十二位置法编排，在不考虑转台各项误差因数的情况下，计算得到各项误差结果，如表1 所示.

表1 不考虑转台误差的参数辨识结果

对三轴转台进行测量后，得到各项误差为Δφy1=3.1″，Δφy2c=2.2″，Δθy2s=3.6″，Δφx2=1.6″，Δφz2=1.9″，Δθz3c=2.7″，Δθz3s=-1.1″，Δθx3c=4.0″，Δθx3s=2.2″，Δβ1c=4.0″，Δβ1s=5.5″，Δβ2c=2.0″，Δβ2x=-2.1″，Δγ1c=-2.5″，Δγ1s=-2.2″, Δγ2c=1.1″，Δγ2s=1.2″，把各项误差项代入计算后得到的各项误差因数如表2 和表3 所示.

表2 考虑转台误差的参数辨识结果

表3 前后对比修正量

5 结 论

1)本文基于多体系统理论建立三轴转台误差模型，列出转台系统的低序体阵列，详细分析三轴转台各类误差，包括几何误差和运动误差等.

2)阐述陀螺标定原理，计算MEMS陀螺输入量，进而推导出MEMS陀螺标定全参数误差模型.

3)编排标定路径进行实验，采集MEMS陀螺单位时间的角速率输出，经过计算得到考虑转台误差参数和忽略转台误差参数时的MEMS陀螺的标度因数、安装误差及零偏等，对比得到两者偏差，可以通过该误差对MEMS陀螺误差模型参数进行补偿，提高MEMS陀螺标定精度.