基于正则化Logistic回归模型的幸福感指数影响因素分析
2021-04-01项超孙珂祎吕鹏飞王延新
项超,孙珂祎,吕鹏飞,王延新
(宁波工程学院 理学院,浙江 宁波315211)
0 引言
随着大数据时代的到来,在自然科学、人类学和工程学等领域的数据集越来越丰富,数据结构日趋复杂。这些数据的主要特点是数据的维数很高,往往大于样本量;并且随着维数的增加,噪声积累,存在虚假相关。范剑青指出高维回归模型中系数存在稀疏性,即绝大部分解释变量的系数为0,因此需要通过变量选择的方法建立稀疏模型,以提高模型的解释能力和参数估计的精确度。
变量选择是从众多变量中选择重要的相关变量来达到稳健建模的方法,传统的变量选择方法如最优子集选择、逐步回归等方法在维数较高的情况下存在计算量大,变量选择不稳定等缺点[1-3]。近些年,统计学家们提出基于惩罚函数的正则化变量选择方法。Tibshirani[4]提出的LASSO是一种最常用的稀疏化手段,主要在于它的可解释性和预测的有效性,并且本身是凸优化问题可以快速求得最优解。但LASSO对较大系数的估计是有偏差的,并且不一定满足oracle性质[5],故Zou提出自适应LASSO,自适应LASSO是无偏估计[6]。高维数据经常遇到变量之间的共线性问题,使得LASSO表现不够理想,2009年,Zou和Hastie提出了弹性网(Elastic net)。此外各种非凸罚函数如SCAD[5]、MCP[8]、SICA[9]和EXP[10]等相继被提出。
幸福是人类千百年来生生不息的追求,幸福生活与每个人的生存与发展息息相关。每个人对幸福感都有自己的衡量标准,过上美好幸福的生活是广大人民群众的希望。何为“幸福”,幸福是人们对于生活各个方面的满足感,从马斯洛需求层次理论来说,人的需求被分为生理需求、安全需求、社交需求、尊重需求和自我实现需求,只有这五大需求得以满足,才能说的上真正意义上的幸福。目前,我国居民幸福感处于什么状态,哪些因素对人们的幸福感有影响,不同人之间幸福感是否有差异,都是围绕幸福这一问题展开。如果能发现影响幸福感的共性,生活中将多一些乐趣;如果能找到影响幸福感的影响因素,便能优化资源配置来提升国民的幸福感。
本文基于CGSS项目的公开数据的问卷调查结果,结合LASSO、SCAD和MCP罚构建正则化Logistic回归模型,研究幸福感的主要影响因素。
1 模型建立
1.1 Logistic回归模型
Logistic回归模型是一种广义的线性回归模型,用来分类0-1问题,也就是预测结果是0还是1的分类问题。设yi和xi=(xi1,…,xip)分别是响应变量和解释变量,i=1,2,3,…,n,yi∈{1,0},同时假设yi和xij相互独立,Logistic回归可表示为:
其中
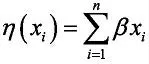
则Logistic回归的对数似然函数为:
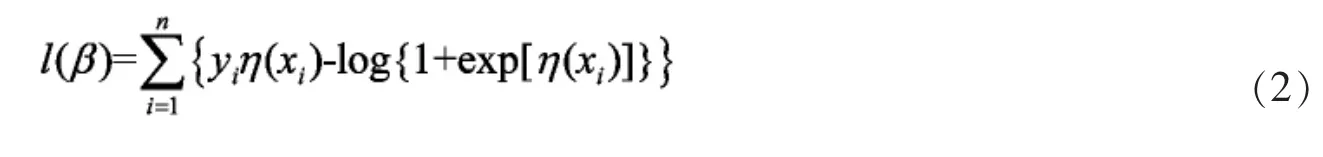
1.2 正则化Logistic模型
对于Logistic回归模型,响应变量yi∈{1,0},y的期望依赖于函数假设
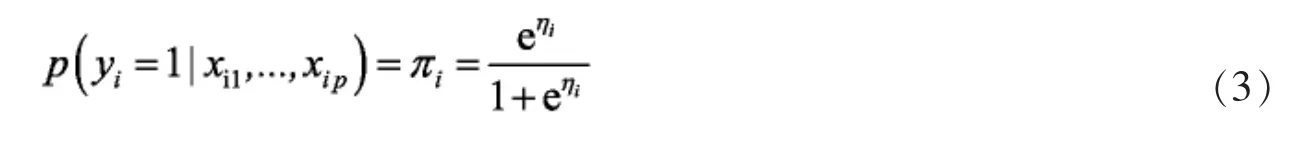
基于惩罚函数的Logistic模型的一般框架为
文中对椭圆拟合法进行了深入研究,针对其容易受到噪声干扰和鲁棒性差的问题,提出一种改进的适合于红外图像的瞳孔定位算法,通过形态学运算、斑点干扰去除等提高算法的抗干扰性。
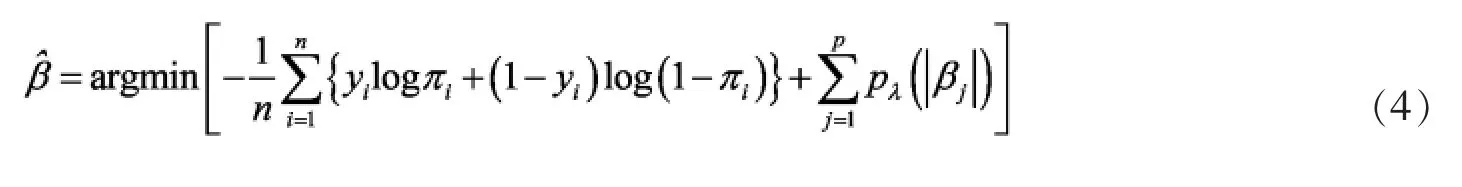
Tibshirani[4]提出的Lasso是一种最常用的稀疏化手段,主要在于它的可解释性和预测的有效性,并且本身是凸优化问题可以快速求得最优解。LASSO罚函数定义为

Fan和Li[5]指出一个好的罚函数应该同时具备三种性质,即连续性、无偏性和稀疏性。但Lasso对较大系数的估计是有偏的,并且不一定满足Oracle性质,故Fan和Li提出了SCAD罚函数,SCAD罚函数如下:
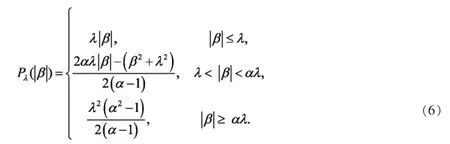
其中,对于给定的λ>0,α>2,SCAD罚函数是分段函数形式,分别对应常数、线性函数和二次函数。SCAD在区间(-∞,0)∪(0,+∞)上是连续可微的罚函数,但在原点处是奇异的,并且在区间[-αλ,αλ]处的导数为0。
MCP估计与SCAD估计类似,MCP估计也具有连续性、无偏性和稀疏性等性质。MCP罚函数如下[8]:
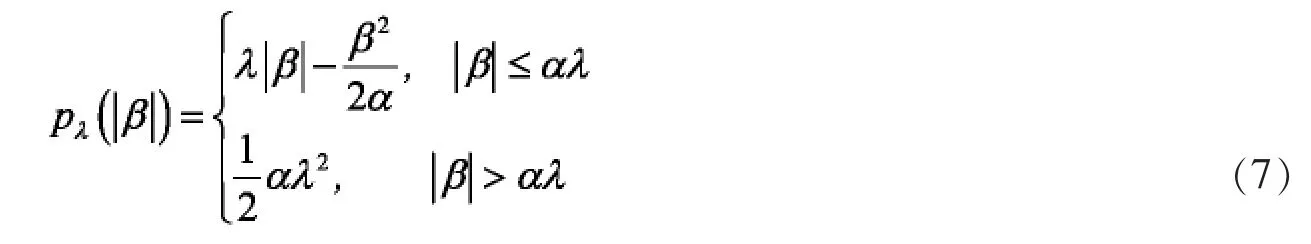
λ≥0决定惩罚的大小,α是影响惩罚范围的调整参数。MCP罚函数满足近似连续性,
2 坐标下降算法
本本文考虑利用坐标下降算法[11]求解SCAD,MCP及LASSO估计问题。坐标下降法是一种非梯度优化算法,其基本思想为:在每步迭代中沿一个坐标方向进行线性搜索,与此同时固定其他坐标方向,再循环使用不同坐标方法从而达到目标函数的局部极小值。
考虑目标函数
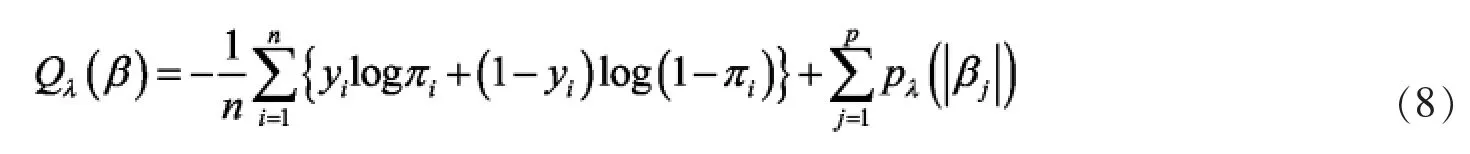

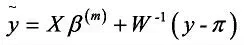
W为关于加权函数的对角矩阵,其对角线上元素为

其中π由β(m)估计。
对于LASSO的坐标下降步为

同理,对于SCAD罚的坐标下降步为
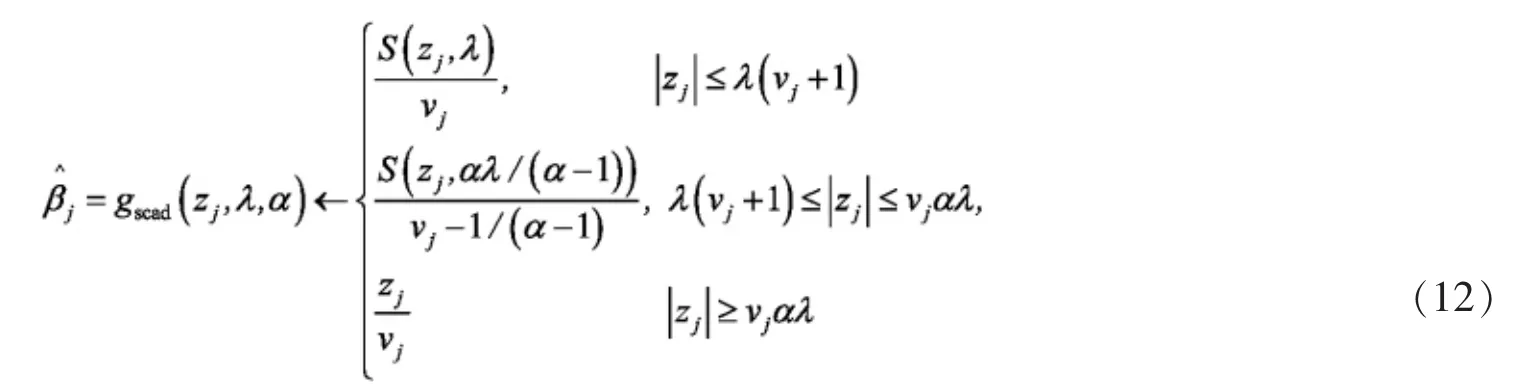
其中α>1+1/vj。对于MCP罚为
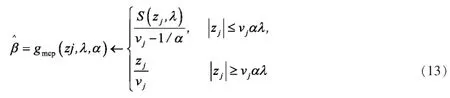
其中α>1/vj。
基于上述,完整的罚Logistic回归的坐标下降算法如下(以SCAD罚为例):
Step 1.按递增方式输入一系列的λ值Λ={λ1,…,λL}和α值Г={α1,…,αk},并定义λL+1,使得

(ii)递减k值
Step 3.递减l
Step 4.对于所有的(λ,α)∈Λ×Г,返回解β^(λ,α)。
在上述算法中,对MCP估计,只需要将其中的gscad(zj,λ,α)换成gmcp(zj,λ,α)即可,而对于LASSO估计,不存在参数α,因此在上述算法中对于LASSO估计,不存在内循环的问题,过程更简洁。此外需要指出的是,在上述算法中设计正则化参数λ和α的选择,本文利用交叉验证的方法选择正则化参数。
3 实证分析
3.1 数据来源及变量解释
本文数据来自中国人民大学中国调查与数据中心主持之“中国综合社会调查(CGSS)”(2015)项目的公开数据的问卷调查结果,中国综合社会调查为多阶分层抽样的截面面访调查。数据具体包括个体的幸福感、性别、年龄、健康状况、受教育程度、就业状态、婚姻状况、户口、家庭社会经济地位等[12]。由于有些问卷数据无意义,所以处理后的有效数据是6 645行数据。数据的获取平台是阿里云天池平台。
选取的预测变量总共有以上29项,分为五项指标。其中性别、所在省市、样本类型、出生日期、民族属于个人基本情况,宗教信仰、教育程度、用在社交上的空闲时间、用在放松休息上的空闲时间、用在学习上的休息时间属于文化生活,个人年收入、住房面积、家庭年总收入、家庭人口、家庭经济状况档次、房产数量、汽车数量属于经济生活,身高、体重、健康状况、心情沮丧的频繁程度属于健康状况,对当今社会是否公平的评价、个人社会地位评价、工作经历及状况、婚姻状况、与同龄人相比的社会经济地位、与三年前经济社会地位相比发生的变化、对一些重要事情所持的观点和看法与社会大众一致次数属于人际关系指标。其中心情沮丧的频繁程度从1到5取值,取值越大感到沮丧次数越少。
为讨论问题的方便,响应变量为幸福感指数(happiness)将此划为两个类别,沮丧程度为4和5时划分为幸福,1-3时为不幸福。“不幸福”和“幸福”,分别赋予对应的数值0、1。数据概况以及部分数据指标如表1和表2所示。

表1 数据集概况

表2 数据集部分指标赋值
3.2 变量选择和参数估计
为了建立模型和比较模型的预测效果,本文将数据集切分为训练集和测试集两部分,训练集数据和测试集数据各占一半。从原始数据集随机抽取50%的数据作为训练集,剩下的50%作为测试集,利用训练集数据建立模型,将测试集的数据代入建立好的模型中进行预测,用于对模型预测准确性的外推检验。
利用全变量Logistic模型、LASSO-Logistic模型、SCAD-Logistic模型、MCP-Logistic模型对上述数据进行实证分析,用训练集数据建立模型,变量选择结果见表3。
根据表3的结果,从稀疏性角度看,Logistic全变量模型没有剔除任何变量,结果显示,对于全变量Logistic回归模型,变量survey_type、gender、nationality、religion、income、floor_area、height_cm、socialize、learn、work_exper、family_income、car、marital的系数不显著,反映出该模型包含了过多的解释变量,使得模型复杂;LASSO-Logistic模型剔除了16个变量,选择出13个变量;SCAD-Logistic模型剔除了15个变量,选择出的变量一共为14个;MCP-Logistic模型剔除了16个变量,选择出13个重要变量,相比全变量Logistic模型,Scad-logistic,LASSO-Logistic和MCP-Logistic模型变量的选择更为简洁,模型稀疏性好。
从解释性角度看,LASSO-Logistic模型、SCAD-Logistic模型、MCP-Logistic模型在剔除的变量中,其中有15个共同的变量,说明本次研究这15个变量对这三个模型来说均为不重要变量;三个模型保留了12个共同的变量,进一步说明了这12个指标的重要性。事实上,宗教信仰、社会的公平性、身体健康状况、社会地位、家庭地位、与同年龄人的社会经济地位都会对人们幸福感造成影响。宗教信仰为人们提供价值体系的支柱,对人们进行心理调节,在很大程度上,影响人们的幸福感。“家”是人内心深处的根,家庭和谐是社会和谐的基础与前提,家庭生活满意度是个人幸福、家庭幸福乃至社会幸福的坚实基石。公平、公正、公开的社会管理制度能够最大限度的促进个体自我价值的实现,也会影响人们的幸福感。
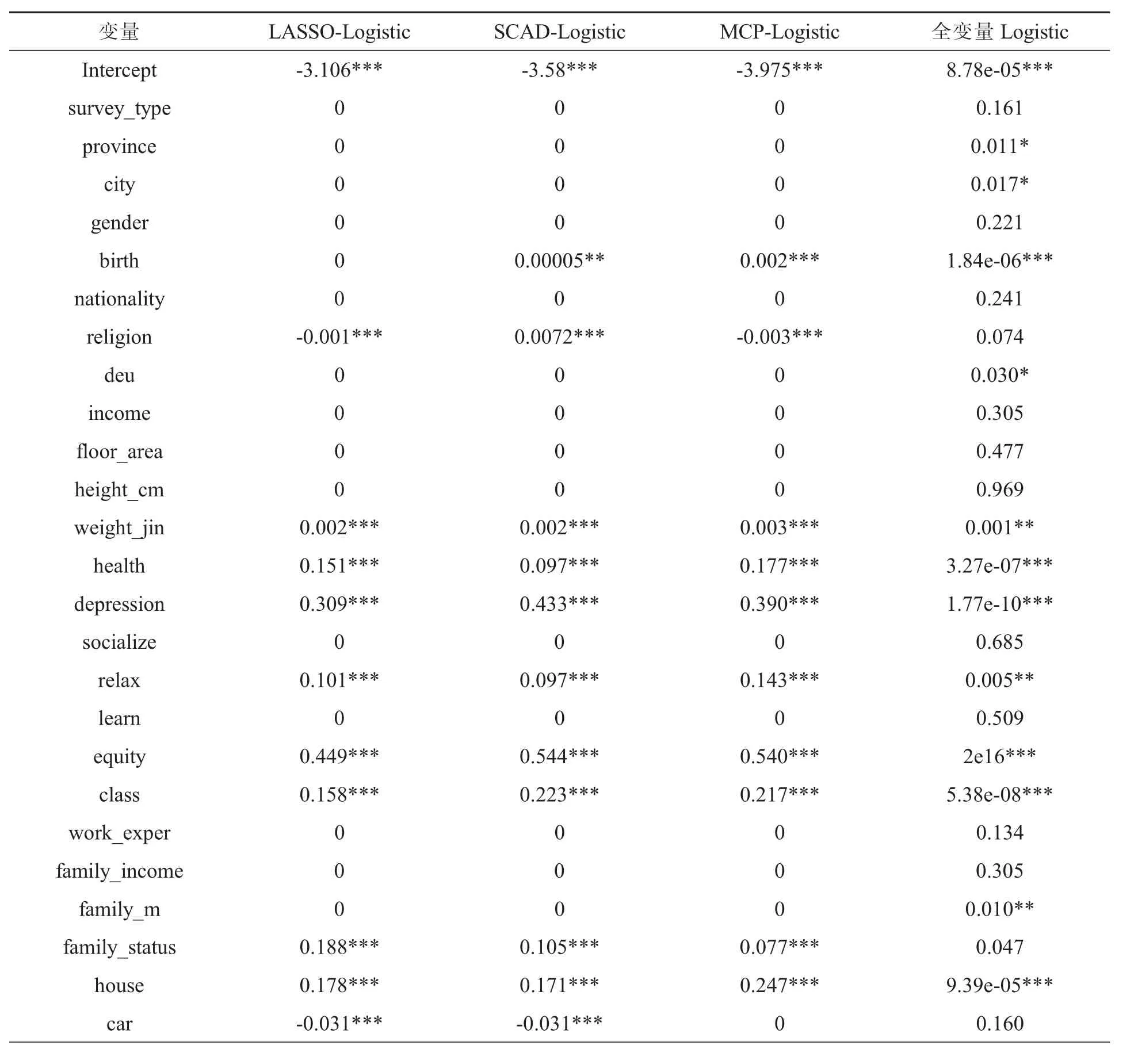
表3 变量选择和参数估计

表3 变量选择和参数估计(续)
3.3 模型准确率比较
根据训练集已经建立好的模型,利用测试集数据分别测试全变量Logistic模型、LASSO-Logistic模型、SCAD-Logistic模型以及MCP-Logistic模型的预测准确率,一般使用混淆矩阵来表示二分类问题预测结果可能出现的四种情况,准确率为预测正确的样本占总样本的比重,表示模型整体的预测效果,准确率越高表示模型的预测效果越好,表4给出了四个模型的准确率,公式如下:
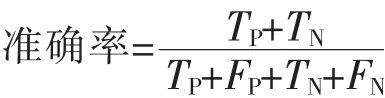
其中TP指的是样本中原本是幸福,模型预测出幸福的个数,TN是样本中原本是不幸福,模型预测数不幸福的个数,FP是样本数据中是不幸福,模型预测出来是幸福的个数,FN是样本数据中原本是幸福的,模型预测出来是不幸福的个数。TP+FP+TN+FN为样本总数。
根据表4可见,从模型预测准确率上来比较LASSO-Logistic模型、SCAD-Logistic模型和MCPLogistic模型的准确率要优于全变量Logistic模型,准确率高出5.56%,由于全变量模型保留

表4 模型预测准确率比较
了所有变量,模型相对复杂,难以剔除一些不重要变量,有一定的过拟合现象,使得模型的准确率低。MCP-Logistic模型的准确率最高为82.15%,优于SCAD-Logistic模型和LASSO-Logistic模型。MCPlogistic模型变量选择更加稀疏,模型的可解释性好、准确率高。因此,从结果的稀疏性、可解释性、准确性三个方面综合分析,本研究认为正则化的Logistic模型更好,特别是MCP-Logistic模型更具优势。
4 结论
本文结合LASSO、SCAD、MCP等罚方法和Logistic回归,构建了正则化Logistic模型,并利用该模型对幸福感指数数据进行实证分析。结果表明,LASSO、SCAD、MCP方法选择了更加稀疏的模型,并且选择出12个共同的重要变量;其次在预测方面,这三种稀疏正则化模型具有更高的准确度,准确率相对于全模型高出近6%。
