基于粒子群算法的滨海盐渍地钉形搅拌桩参数优化分析
2021-04-01邵晗璇马永政梅红蕾霍英龙孙雅琪
邵晗璇,马永政,2,梅红蕾,2,霍英龙,孙雅琪
(1.宁波工程学院 建筑与交通工程学院,浙江 宁波315211;2.浙江省土木工程工业化建造工程技术研究中心,浙江 宁波315211)
0 引言
滨海软土地区受海水浸渍作用地下水矿化度高,在海岸退移以及人工围垦、推填等影响下,可形成滨海盐渍土,相关研究表明不同含盐量会对土体性质参数产生不利弱化影响[1],显然,软土地基处理时需要考虑盐渍土特性的影响。作为软土路基处理的常规方法,水泥土搅拌桩法施工简便、成本低、适用性强,因而应用推广甚多。水泥搅拌桩中的异形桩,是通过正反转搅拌机制,在不同桩段形成大小不等的桩径,形成中字形或钉形的搅拌桩,钉形桩通过扩大头发挥类似承台作用的效果,从而提高搅拌桩承载能力,比常规桩加固效果更好[2-3],具有良好应用价值。
搅拌桩设计要点包括确定桩数、桩径、桩长、桩间距等参数,从而确定置换率参数,以满足单桩和复合地基承载能力、自身强度、沉降变形等要求。对于作为非等直径异形桩的钉形桩,显然不同于等直径桩,需要考虑钉形桩扩大头承台效应,以合理计算表达桩基承载力、复合地基置换率等。通过桩基影响因素作用机理探讨,以便更好地满足设计施工需要,迄今相关研究探索不少,如:苏阳[4]等结合实例探讨平面尺寸和桩长优化问题,建议摩擦型桩在满足下卧层强度验算的要求前提下,采用较短的桩并加大置换率较为有利;裘志坤[5]等基于正交试验研究置换率、桩体刚度、桩长等的关系影响;杨磊等[6]探讨对深层搅拌桩优化分析,确定桩长、基础底面积、置换率的最优数据组合;姚成[3]等通过数值分析对比常规搅拌桩和钉形桩的加固特性,并对后者设计参数进行优化分析。在桩参数优化分析方面,可引入系列非线性优化算法,建立目标函数,基于严谨的优化算法程序分析桩基参数,如王成华等[7]采用粒子群算法,建立桩基础造价目标函数,分析桩基础主要设计参数;简文星等[8]应用该算法类似地研究锚拉桩参数优化问题等,优化分析重点之一是合理处理约束条件。
总的来说,目前尽管在搅拌桩承载机理与设计参数优化分析理论与应用研究方面取得一些成果,但在特殊工况条件如滨海盐渍地、异形桩承载机理特征等方面的研究,仍有待深入。本文借鉴前人关于桩基优化分析思路,主要引入粒子群算法,建立目标函数并引入参数界限值和约束条件,优化分析滨海盐渍地条件下钉形水泥土搅拌桩的设计参数,探讨设计参数的优化组合关系,并结合工程实例进行分析验证。
1 优化算法原理
含约束的最优化极值问题表述如下:

其中:f(x)为目标函数,x=(x1,x2…,xi,…,xm),取值范围xi∈[ximin,ximax],gj(x)为约束函数。
研究引入粒子群优化算法,该算法是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。其遍历算法流程如下:初始化粒子的位置、速度和全局最优信息→根据当前信息计算速度,更新位置等信息→计算目标函数→判断是非满足约束条件→如不满足则调整速度等参数,重新更新;如满足则输出最优位置和目标函数值→直到满足迭代控制条件,结束搜索过程。其中速度和位置进化方程如下:
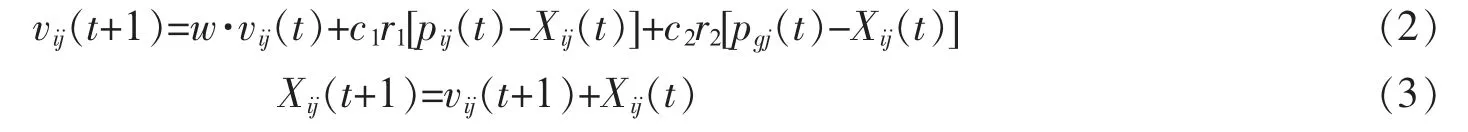
上式中,vij(t)为粒子i的第j维参数第t次飞行速度;Xij(t)粒子i的第j维的位置;w为惯性权重,c1和c2分别为认知系数,r1、r2为0和1之间的随机数;pij(t)为粒子i的第j维参数的个体历史最优位置,pgj(t)为群体i的第j维参数的群体历史最优位置。权值W按线性递减计算如下式(5),其中Wini为初始权值、Wend为最终权值。Gk最大迭代次数,g为当前次数。

对于目标值超越约束边界的飞行粒子,本文拟按下式(5)对该速度乘以线性递减系数μ,以进行折减处理,其中n为当前调整步数,Nk为总调整步数,Δ为调整步长。

2 目标函数设计
本文建立以水泥搅拌桩体积最小化为目标的优化目标函数,约束条件包括单桩和复合地基设计承载力,以及最大地基沉降允许值,待优化桩基参数包括桩大小头直径、桩长、承台(桩大头)高、桩间距等。
2.1 带显式约束条件的目标函数
对单桩来说,设待优化参数为桩大头和下部主桩段的直径D1、D2,以及桩大头设计高度h1;另外以水泥掺量ω作为材料优化参数。表达体积的目标函数A表述如下式所示,其中ξ为下部主桩段与桩大头的代价比,计算时设ξ=1;桩总长为H0。

设桩基承载力Ra、设计承载力为[p0],桩基承载力约束条件即须满足:Ra≤[p0]。对钉形桩来说,桩基承载力可分别按桩材料强度或摩擦端承桩计算如下式(7)-(8)。相关研究表明[8],水泥土强度特别是现场测试强度,对单桩承载力影响最大,一般承载力计算式(7)的结果比(8)的小。

其中系数η范围值0.2~0.33,fcu为桩材料水泥土抗压强度,AP为桩基横截面积,宜取下部桩段对应的横截面积;qc为桩侧土平均摩擦力,qd1、qd2为桩端土极限应力,α1、α2分别为端阻折减系数,Ra可取上两计算式中最小值,且不可小于允许值,即Ra≥[p0]。考虑到海盐含量不同对土体工程性质的影响,本文分析时参照相关文献[9],根据海盐含量的弱化影响,对侧摩阻力qc、端承阻力qd以及材料强度参数进行相应折减以计算桩基承载力。
复合地基设计优化参数包括不同桩群分布形式下的桩间距参数等,设桩群为梅花型布置,桩间距为a,则可取等边三角形区域为单位优化区域,对应桩体积目标函数
2.2 带隐式约束的目标函数
在上节目标函数中,可通过罚法施加隐式约束,从而自动满足约束条件,分别建立单桩和复合地基的优化目标函数如公式(9),其中:单桩目标函数B中包括体积值A和乘以罚参数的桩基承载力约束条件;复合地基目标函数包括桩基体积值以及复合地基承载力与沉降变形约束条件,两式中θ1、θ2为增加的罚系数,宜选择适当值,减少其对优化结果的影响,可作为上一节计算的参照。
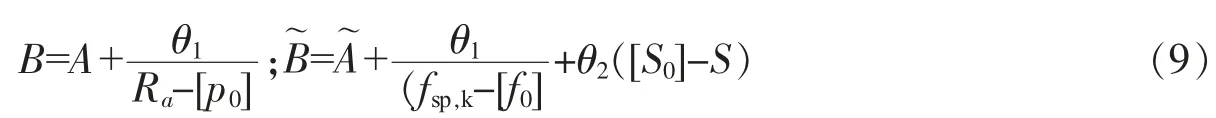
3 案例分析
依托工程为浙东南象山半岛某省道改建工程,设计等级为一级公路;路基宽度24.5~29 m,局部软土路基路段经过滨海滩涂盐渍地区,土层参数如表1所示。采用钉型水泥搅拌桩加固,设计单桩承载力标准值不小于170 kN;复合地基承载力标准值不小于150 kN,最大沉降量为桩长1.0‰~2.0‰(实际取1.5‰),施工搅拌桩长约为12.0~15.0 m左右,则沉降量不超过18~30 mm。①~③2为桩基长度范围的地层,计算加权黏聚力15.38 kPa、摩擦角12.23°、压缩模量3736.5 kPa;③4、④1、④2为软弱下卧层。取水泥土平均抗压强度2.0 MPa,桩基弹性模量为540 MPa,平均侧摩阻力q=Σhiqi/Σhi=23.5 kPa,端阻力q1和q2分别为65.0 kPa和85.0 kPa。相关文献[1]的实验研究表明,以象山滨海软土为例,不同海盐含量对地基土层性质以及搅拌桩强度等性能的影响如表2所示,其中水泥固化海盐土强度随含盐量的变化规律如图1所示(参照相关文献[1]),假设地基承载力、桩侧桩端部受海盐含量的弱化影响规律与土层粘聚力和内摩擦角的类似。
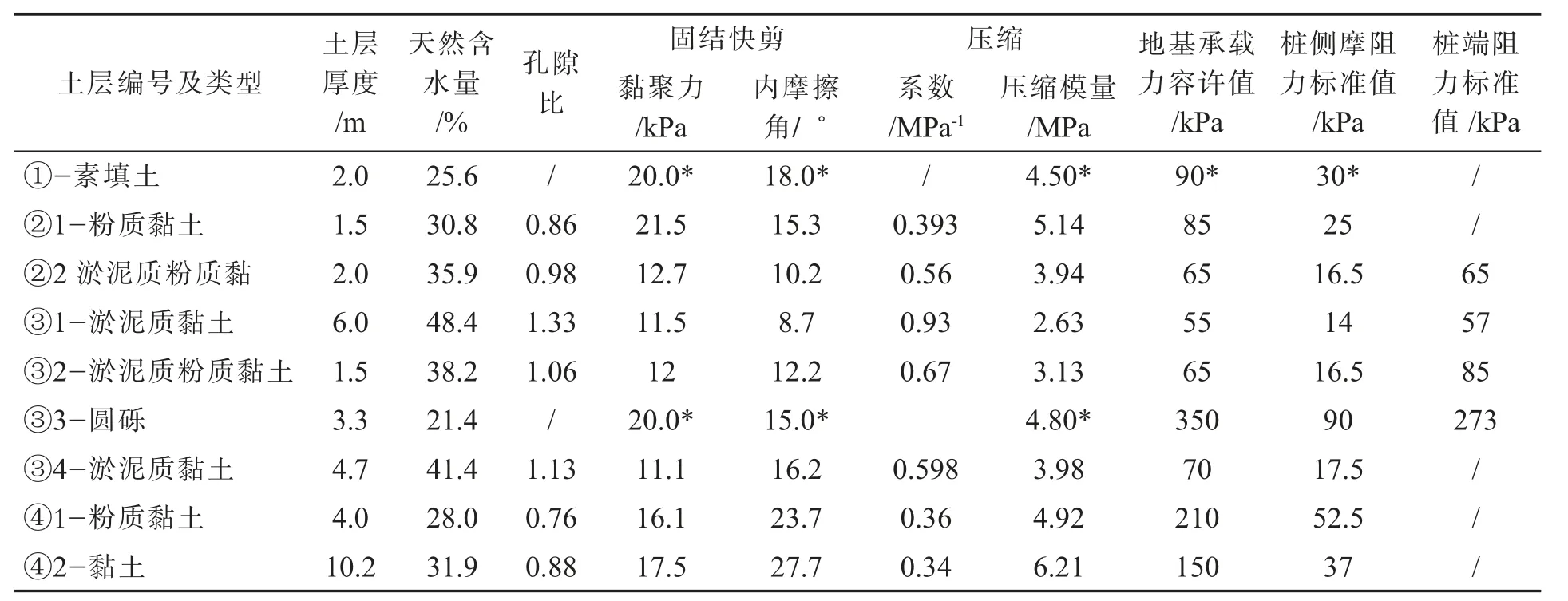
表1 主要土层物理力学属性

表2 含盐水泥土参数弱化系数[1]

图1 水泥固化海盐土的强度随含盐量变化关系[1]
桩基设计优化参数取值范围:桩大头直径D1(0.8~1.5 m);桩小头直径D2(0.5~1.0 m);承台高h1(2.5~4.0 m);桩长H0(12.0~18.0 m);桩位平面间距a(1.5~3.5 m)。桩基模型其他参数取值如下:桩端承载系数α1=α2=0.45;水泥土抗压强度2.2 MPa,单桩承载力计算系数η取0.3;复合地基等效系数ζ取0.6,折减系数β为0.85。粒子群优化计算参数如下:粒子数为50,w值范围0.5~0.9,c1=c2=2.0,超界限的调整步长Δ=±0.005,总调整步数设为200。
3.1 单桩分析结果
定义条件A为无约束情形下的优化分析,可作为有约束计算的对照;定义条件B为含承载力约束条件优化分析,即分别按摩擦端承桩计算承载力(简称为承载力计算A)和材料强度特性计算承载力(称为承载力计算B)两种情况计算,一般按承载力B计算结果相对偏小,因此是承载力计算的主要依据。优化计算结果见表3,可以看出:①在无约束的条件A情况下,桩径、桩长以及大头高度均取最小值时,目标函数值最小,含盐量增加对承载力的弱化影响可不计。②在有约束的条件B情况下,下部桩径参数因含盐量变化对材料强度影响而发生相应改变,其他参数不变。
以含盐3%的条件B优化分析为例,粒子群飞跃过中逐渐收敛,在飞行第1步次,各粒子两组约束值计算结果明显分散,但都不低于约束界限,因此无越界调整次数。飞行第20步次时,如图2所示,各粒子两组约束值计算结果趋于收敛,部分粒子有越界,需往回调整,一般回调1~2次即可。进一步飞行至第200步次时,计算结果明显收敛,且越界调整次数仍很少,说明迭代步内回调搜索算法可行。
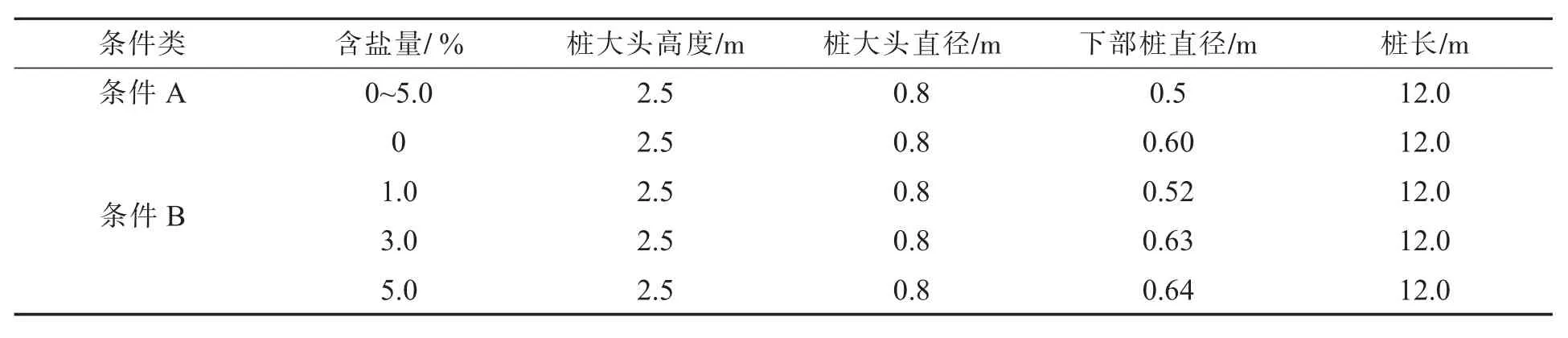
表3 桩参数优化计算结果

图2 单桩第20次飞行内调整情况
3.2 复合地基分析结果
同样地,可定义复合地基分析时无约束条件的情况为条件C,带约束的为条件D,约束条件包括考虑满足单桩和复合地基承载力,及沉降变形等。粒子群飞跃过程,除了两组单桩承载力计算值Ra发生收敛变化,还包括复合地基承载力fsp,k以及沉降值两个受约束量的飞行迭代变化,类似地,从飞行第1次、20次,各个约束值结果逐渐收敛,如图3所示。
统计飞行步中越界调整粒子个数以及平均调整次数如图4所示。可以看出,随着飞行次数增加,开始阶段(指飞行0~20次)的越界粒子急剧增长,但平均调整次数总的来说较小,局部存在明显起伏;中间阶段(飞行20~200次)的越界粒子数稳定在高位,平均调整次数不大(不排除个别粒子自身调整次数大),起伏幅度不高;后期阶段(大于200次)随着优化目标逐渐明确锁定,越界粒子数目逐步下降,粒子逼近约束边界,平均调整次数很小,但个别飞行次起伏幅度颇大。再从各次飞行中全部粒子的越界调整分布情况统计图(图5)可看出,单次飞行中一般粒子调整次数不超过5次,超过10次的较少,只有极个别粒子需要调整超过50次(注:第1次飞行时,无粒子触越边界),表明越界调整算法是可行的。
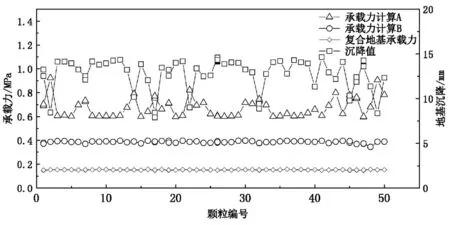
图3 复合地基第20次飞行内调整情况

图4 飞行中越界调整的粒子数及调整次数
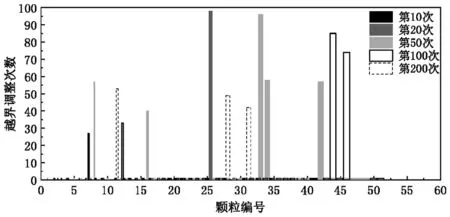
图5 飞行中粒子位置调整次数分布情况
复合地基优化分析结果如表4。结果表明:无约束条件下,优化参数均取到边界值,其中桩间距取最大值,且都对含盐度变化影响不敏感。在约束条件下,优化规律结果表明:桩大头高度趋于取上限值;桩大头直径一直无变化,取下限值;下部桩径取上限值,且对含盐度变化不敏感;桩长对优化影响因素不敏感;桩间距随着含盐度增加的弱化影响,趋于变小。上述优化结果需要结合工程实际进一步验证。实际取值可以对优化结果按整数或指定小数位进行取值[10]。
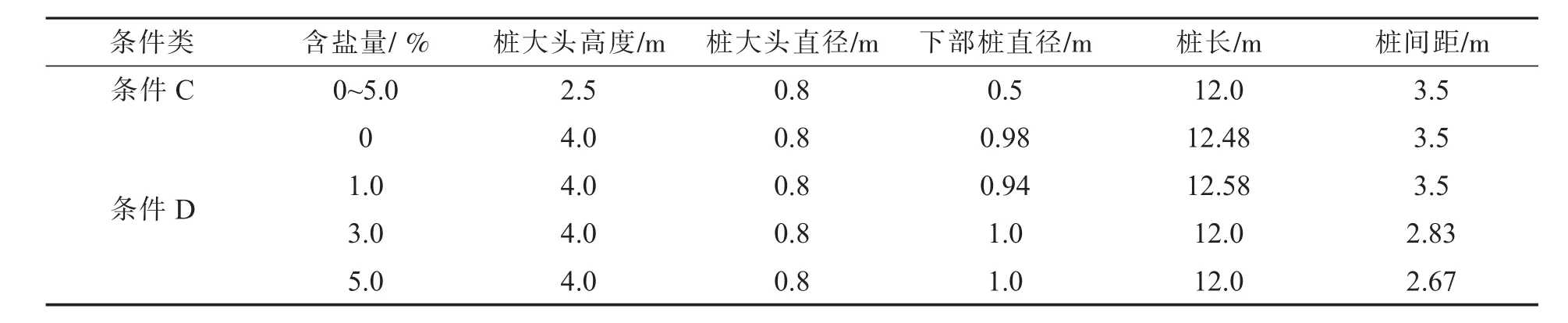
表4 复合地基参数优化计算结果
4 结论
本文针对滨海盐渍地钉形水泥土搅拌桩设计参数优化问题,基于粒子群算法建立优化分析模型,结合具体案例分析探讨了盐渍地环境下搅拌桩优化设计参数,得到如下主要结论:
(1)建立了以搅拌桩体积最小化为目标的单桩和复合地基优化函数,引入显式或隐式约束条件以表达单桩或复合地基承载力以及沉降量的界限值要求,其中引入隐式约束条件时会带来新增的罚参数计算敏感性问题;
(2)针对部分粒子群飞行过程中不满足约束条件的情况,提出了越界粒子飞行速度反向线性折减以调整到界内的搜索算法,算例结果表明调整算法是可行的;
(3)优化结果表明,滨海软土因高含盐量(1%~5%)使得土体参数有10%~30%弱化折减的情况,对单桩或复合地基来说,下部桩径和桩大头高度应取设计尺寸上限值;桩长、桩大头直径无影响,可取常规设计值;复合地基的桩间距宜根据含盐量增大而相应调小0~21%。
