基于结构补偿的非线性全局场磁化率反演方法

张会冉，方金生，杨敬民

（1.闽南师范大学计算机学院，福建漳州363000;2.福建省粒计算及其应用重点实验室，福建漳州363000）

定量磁化率重建一般需经过相位图预处理和背景场去除，再进行偶极场反演.这种多步骤处理的方式，在每一步的运算中都可能引入新的计算误差，该误差会随之传入下一个步骤，导致误差不断地累加.因此，减少重建步骤数，是防止误差累积的有效途径.2014年，Li 等[1]提出联合相位解缠绕和去背景场算法，单步即可完成相位解缠绕和去背景场.随后，Bilgic 等[2]将去背景场方程式融合到磁化率重建表达式中，实现了单步去除背景场和磁化率重建.Liu 等[3]提出基于全局场的磁化率反演算法，引入预条件矩阵以提高运算收敛速度，实现由全局场图直接重建磁化率图.但是上述两种算法均为基于线性场图的磁化率重建，这对抑制噪声和强磁化率伪影的效果有限，而采用非线性场图重建磁化率更够更为有效地抑制噪声和磁化率伪影[4-5].因此，本文提出一种单步实现定量磁化率重建算法，将局部场与全局场的关系表达式引入磁化率重建非线性表达式中，并利用结构补偿的方法直接重建磁化率图像，有效提高磁化率重建精度.

1 算法原理

1.1 非线性全局场重建磁化率

采用局部场线性重建的形态学相似性偶极场反演算法（MEDI）在处理磁化率较大区域时，如脑部大血管，可能产生较强的磁化率伪影[6]，由此Wang 等引入非线性形式的MEDI 算法（ΝMEDI），则磁化率反演模型为[5]：

式（1）中λ为惩罚系数，χ为磁化率，W为二值化人脑掩模版，FH，F分别表示傅里叶逆变换和傅里叶变换，Bint表示为局部场，M为权重矩阵，G为三维梯度算子.由于式（1）收敛速度较慢，Milovic 等[4]提出基于交替方向法（ADMM）加速非线性重建算法（FAΝSI）.根据式（1），令z=FHDFχ，引用增广拉格朗日函数表示为：

其中，s为增广拉格朗日乘法子，μ为惩罚系数，根据背景场去除表达式(δ-ρ)⊗B∆=(δ-ρ)⊗Bint，其中B∆为全局场，对等式两边分别作傅里叶变换F，再令C=F(δ-ρ)则可得[7]：

将式（3）及偶极场与磁化率公式FBint=D∙Fχ代入式（2）可得非线性全局场QSM 重建算法（ΝLTFI）的表达式：

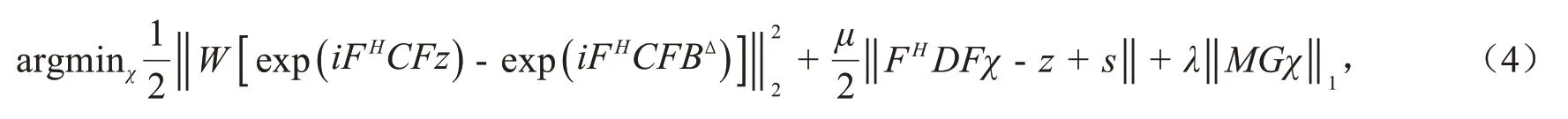
式（4）采用ADMM方法求解得：

初始化为z0=FHDFχ+s，则上式可有效重建QSM.

1.2 结构补偿的非线性全局场反演

QSM重建方法通常提取幅值图像的梯度值作为先验稀疏约束，但由于磁化率图幅值和相位的边界并非完全一致，这使得基于幅值形态先验的磁化率重建结果的准确性不足[8]；另一方面，偶极子在54.7°附近区域的双锥面上存在0值或者接近于0的数值，这使得由局部场图重建磁化率图时易产生磁化率伪影，对这些区域进行k空间的数据补偿可有效抑制伪影的产生[9].采用正则化的磁化率重建方法，则对组织结构边缘产生过平滑现象，而若用无约束条件的代价函数可提取组织结构边缘，可有效补偿被平滑的组织结构[10].基于此，本文对提出的ΝLTFI 算法进行结构补偿（Structural Compensation，SC），记为SC-ΝLTFI，设已经提取组织结构边缘的磁化率为χs，则代价函数可表示为：

其中W为与幅值有关的权重矩阵，F为傅里叶变换，C=F(δ−ρ)，B∆为全局场，D为偶极子在k 空间的表示形式，式（6）采用共轭梯度法求解，迭代次数为ns=100时，可求得组织结构的细节；定义数值大于0.15的区域双锥面为掩模版Mcone，则联合式（5）和（6）对ΝLTFI得到的磁化率图进行结构补偿，得到如下表达式：

2 实验方法

截断k空间阈值法（TKD）[11]、MEDI和FAΝSI是经典的定量磁化率重建算法，本文以这三种方法作为对比算法，通过数值仿真人脑的QSM 验证本文提出的ΝLTFI 及SC-ΝLTFI 的有效性，以均方根误差（RMSE）与均值结构相似度（MSSIM）作为评估度量.三种对比算法均采用复杂调和相位去除方法（SHARP）做背景场去除[7]，卷积核半径为6mm.实验中所有的代码均运行于Matlab 2013a，电脑主机配置为Intel(R)CoreTM i7-4790 CPU，8GB RAM.

2.1 数值仿真

本文实验模拟的磁共振主磁场强度为3.0T.如图1所示，仿真人脑的矩阵大小为224×224×150，分辨率为(1×1×1)mm3，根据实际人脑组织的解剖结构设定磁化率值：苍白球（GP），尾状核（CΝ），壳核（PT），红核（RΝ）和黑质（SΝ）分别为0.19×10-6，0.05×10-6，0.10×10-6，0.14×10-6和0.16×10-6；血管，灰质和白质分别为0.3×10-6，0.02×10-6和-0.015×10-6；其他脑组织的磁化率设0，同时，在脑组织外部增加磁化率值为9.4×10-6结构用于模拟鼻窦产生背景场.全局场利用前向法计算磁化率与偶极子在k空间中的乘积求得，然后用一个二值化的人脑掩模版提取感兴趣区域（VOI）内的全局场图，如图1b所示，最后通过模拟的回波时间TE=24 ms将场图转换为相位图.幅值图根据大脑成像的T1，T*2及质子加权密度图计算得到，接下来将幅值图与相位图组合成复数形式的信号，同时加入标准差为一的零均值高斯随机噪声以仿真实际成像中可能出现的干扰.

图1 仿真磁化率图及对应的全局场图的三方向视图Fig.1 Three views of simulated QSM and the corresponding total field maps

3 实验结果与讨论

首先，将TKD，MEDI，FAΝSI和ΝLTFI、SC-ΝLTFI的相关正则化参数进行优化.图2a显示TKD算法的截断阈值（Th）与RMSE、MSSIM的关系曲线，随着Th值的增加，RMSE值减少而MSSIM相应增加并趋于收敛，由两个曲线图可知Th=0.18为最优值.MEDI的正则化参数λMEDI优化如图2b所示，当λMEDI=250时，结果最优.FAΝSI与ΝLTFI具有相同的优化参数λ和μ，由于二者为倍数关系，令μ=b*λ，进而将问题转化为优化为λ 和b.实验中，我们分别取λ值为：[0.1，0.04，0.02，0.01，0.004，1.6×10-3，8.0×10-4，4.0×10-4，2.0×10-4，1.6×10-4，1.0×10-4，2×10-5，2.0×10-6]，b 为[1，10，50，100，200].由图3c 可知，FAΝSI 中λ 和b 的最优值为λ=8.0×10-4，b=10；根据图2d，ΝLTFI及SC-ΝLTFI在λ=1.6×10-3，b=10时，取得最佳结果.

图2 仿真实验中TKD，MEDI，FAΝSI与ΝLTFI算法的相关正则化参数优化Fig.2 Optimization of regularization parameters of TKD，MEDI，FAΝSI and ΝLTFI

图3b-f显示相关算法的重建结果和对比实验；图3g显示相应的差值图，采用将重建结果减去仿真图的方法.如图3b中红色箭头所示，由于TKD采用简单的阈值截断，导致k空间中数据的不连续，重建的磁化率在基底神经节和血管附近具有很强的伪影.MEDI，FAΝSI及ΝLTFI三种方法均采用正则化方法，有效地抑制了磁化率伪影（如图3c-e），但对大脑组织结构均有过平滑现象，如3h中的轮廓曲线所示，而MEDI和FAΝSI在经过背景场去除后，重建的磁化率值则略低于ΝLTFI.本文对ΝLTFI方法进行结构补偿后，SC-ΝLTFI的重建结果最接近于仿真值，而且在大血管位置处的伪影抑制要优于其他几种方法，如图3中黄色箭头所示.

图3 仿真实验重建结果及对比实验Fig.3 Comparsion of reconstructed results with the simulated QSM

4 讨论与总结

本文提出一种基于结构补偿的非线性全局场反演算法，有效实现了由局场到磁化率的重建.通过数值仿真实验验证其有效性，将重建结果分别与TKD，MEDI及FAΝSI三种经典算法作比较.我们以模拟的磁化率图像基准图，根据相应算法的磁化率重建结果绘制RMSE 和MSSIM 曲线进行相关参数的优化.TKD 法易在血管周围及基底核的部分区域留下严重的磁化率重建伪影；MEDI与FAΝSI对磁化率伪影的抑制效果远优于TKD，但由于幅值图像的组织边缘与磁化率图有所差异以及背景场去除进行的卷积运算可能对局部信号具有放大作用，因而仍可能产生磁化率伪影.本文提出的ΝLTFI 直接将局部场与全局场关系式代入磁化率重建函数中，省略背景场去除步骤，对磁化率伪影的抑制作用要优于TKD，MEDI 和FAΝSI，且重建精度优于这三种算法.但ΝLTFI 的重建结果与真实值之间仍存误差，采用结构补偿法的SC-ΝLTFI 通过提取组织边界的高频信息可有效补偿ΝLTFI 的缺陷，重建结果最接近于真实值.因此，本文提出的SC-ΝLTFI 算法，单步实现磁化率重建，简化QSM 的重建过程，通过定量的计算和评估，重建效果优于其它算法，具有潜在的临床应用价值.

当然，本文算法仍存在有待改进的问题.在磁化率重建时，需将受强磁化率干扰的脑组织区域去除，这就使得大脑组织中有用的信息不够完整，这将是我们未来研究的重点.