PM紧邻极值Brick

邓家宏

（1.闽南师范大学数学与统计学院，福建漳州363000;2.数字福建气象大数据研究所，福建漳州363000）

本文讨论的图均为简单图.若不加特殊说明,均默认采用文献[1]中的记号.具有n个顶点的圈Cn上的每一个顶点与孤立点K1进行连边得到的图Wn称为轮图，并当n为奇数时候称为奇轮.一个图G中的匹配M是指一些不相邻边的集合,当某个匹配M饱和了图G中所有的点,那么我们称这个匹配M为图G的一个完美匹配.图G中全体完美匹配构成的集合我们用ℳ(G)来表示.∀X⊂V(G),用∂(X)表示以X为一侧的边割,即图G中恰好一个端点在X中的所有边组成的集合.用E(X)表示图G中两个端点都在X中的所有边组成的集合.

对一个图G而言,当它是连通的,且至少有两个点,并满足G中任一边,都属于G中某一完美匹配,则称图G为匹配覆盖图.若图G的一条边属于且只属于图G的一个完美匹配,我们称其为图G的solitary边.图G中所有完美匹配的关联向量,通过整数ℳ(G)线性组合形成的空间,称为图G的匹配格.我们把由匹配覆盖图G生成的匹配格的维数记为dim(G).若|ℳ(G)|=dim(G),则称图G为匹配覆盖极值图，本文简称为极值图.关于匹配格，可以详见文献[2].

下面介绍PM紧邻的定义.首先按如下方法定义G的完美匹配图PM(G)：把ℳ(G)中每个完美匹配作为PM(G)的顶点,当图ℳ(G)中的两个完美匹配M1和M2的对称差M1ΔM2恰好为一个(匹配)交错圈时,PM(G)中两个顶点M1,M2相邻.特别地,当PM(G)为完全图时,即对∀M1,M2∈ℳ(G),都满足M1ΔM2恰好为一个交错圈时,则称图G为PM紧邻.文献[3]证明了该PM紧邻的定义与摘要中的定义等价.

在图G中,∀X⊂V(G),令C=∂(X),我们把X收缩为一个点x后,所得到的图记为G{Xˉ;x},当不需要强调点x时候,可以简记为G{Xˉ}.类似地,我们可以把Xˉ收缩为一个点xˉ的图记为G{X;xˉ}或简记G{X}.我们把G{Xˉ;x}和G{X;xˉ}叫做图G的C收缩.若匹配覆盖图G关于边割C=∂(X)进行C收缩后得到的图G{X}和G{Xˉ}都为匹配覆盖的,则称边割C为G的分离割.

在匹配覆盖图G中,当一个边割C=∂(X),满足对任何M∈ℳ(G),都有|C⋂M|= 1,则称C为G的紧割.可以证明紧割都是分离割,而反之不对[4].显然在匹配覆盖图中,当X或Xˉ为单点时,边割C总是紧割,把这样的紧割称为平凡的,而其余的称为非平凡的.依据是否为二部图,把没有非平凡紧割的匹配覆盖非二部图称作brick,没有非平凡紧割的匹配覆盖二部图称作brace.更特别地,当brick中的分离割都是紧割时,我们称这个图为solid brick,否则称之为nonsolid brick.

当一个匹配覆盖图G有非平凡紧割C=∂(X)时候,可以把G进行C收缩分解为G1=G{X}和G2=G{Xˉ}.当G1或G2中仍然有非平凡紧割的时候,该分解过程可以一直进行下去,直至分解得到的任何一个图,都不存在非平凡紧割.依据定义,这样分解得到的最终图,要么是brick,要么是brace.可以证明这样的分解的最终结果,在不考虑重边的时候是唯一的[2].把图G分解到不能再分解时的brick数记为b(G),不产生歧义时简记为b.若图G关于分离割C进行C收缩后得到图G1和G2满足b(G1)=b(G2)= 1,则称分离割C为robust割.

1 预备知识

引理1[4]所有的极值solid brick均为奇轮.

引理2[5]所有的极值solid brick均为PM紧邻的.

证明由引理1,所有的极值solid brick均为奇轮,不妨记这个奇轮为W2k+1.它是由轮圈C=(v0,v1,…,v2k,v0)上的点全部连边到轮心h而成.显然连接到轮心的边都为solitary边,故任取两个完美匹配M1,M2,其中hvi∈M1,hvj∈M2,i)当i=j,此时M1=M2故M1ΔM2=∅,即为一个平凡交错圈；ii)当i≠j时,vi和vj把轮圈划分为一条奇路P1和一条偶路P2,其中P1⋂M1=P1⋂M2,(P2⋂M1)⋃(P2⋂M2)=P2.则M1ΔM2=P2⋃{hvi}⋃{hvj}为一个交错圈.根据PM紧邻定义得证.

注意,在考虑PM紧邻时,由于当取两个相同的完美匹配M1,M2作对称差的时候,总有M1ΔM2=∅,而∅是一个平凡的交错圈.所以在接下来关于PM紧邻的讨论中,我们总是假定作对称差的两个完美匹配是不相同的.

引理3[4]若图G是一个brick,C是一个robust割,G1,G2是图G经过C收缩后得到的两个图,那么图G是极值图当且仅当i)G1,G2都是极值图；ii)C中的每一边至少在G1或G2中为solitary边；iii)G有且仅有一个完美匹配包含C中的一条以上边.

引理4[4]每一个极值nonsolid brick,都有一个robust割C=∂(X),使得G{X}是一个奇轮,G{Xˉ}是一个极值brick.

引理5[1]在一个图中,每一个圈都与任意边割有偶数条公共边.

2 主要结果

定理1任何的极值brick均为PM紧邻.

证明反证法，假如存在极值brick不是PM紧邻的,不妨取当中点数最小的一个图G.由引理2,极值solid brick均为PM紧邻的,故此时只需假设G为极值nonsolid brick进行证明即可.由引理4,图G存在一个robust割C=∂(X),X⊂V使得G1=G{X}为奇轮(它同时也为一个极值brick),G2=G{}为一极值brick.注意这里|X|和均必须为奇数,故任意取完美匹配M都有|C⋂M|≥1,且由引理3,有且仅有一个完美匹配M*满足|M*⋂C|=a≥3,其中a为奇数,其余完美匹配M满足|C⋂M|= 1.接下来我们将分情况证明∀M1,M2∈ℳ(G),都满足M1ΔM2为一个交错圈.

情况1|M1⋂C|= 1,|M2⋂C|= 1.

情况1.1 当M1⋂C=M2⋂C={e} 时,由引理3,边e至少为G1或G2中的一条solitary边,不妨假设是G1的.此时M1⋂E(X)=M2⋂E(X),否则,(M1⋂E(X))⋃{e}和(M2⋂E(X))⋃{e}为G1的包含e的两个完美匹配,与e为G1的solitary边矛盾.故

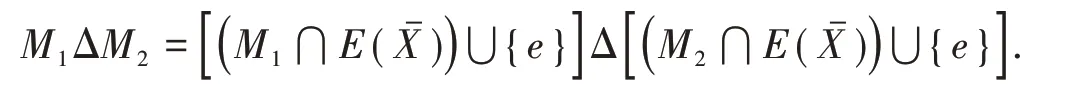
情况1.2 当M1⋂C={e1} ,M2⋂C={e2}(e1≠e2)时,(M1⋂E(X))⋃{e1}和(M2⋂E(X))⋃{e2}分别为G1的两个完美匹配,由图G最小性,它们的对称差为G1的一个交错圈.同理,和的对称差也为G2的一个交错圈.此时,

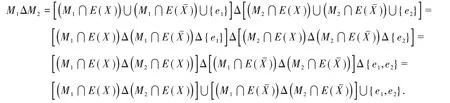
故M1ΔM2此时为图G一交错圈，如图1所示.

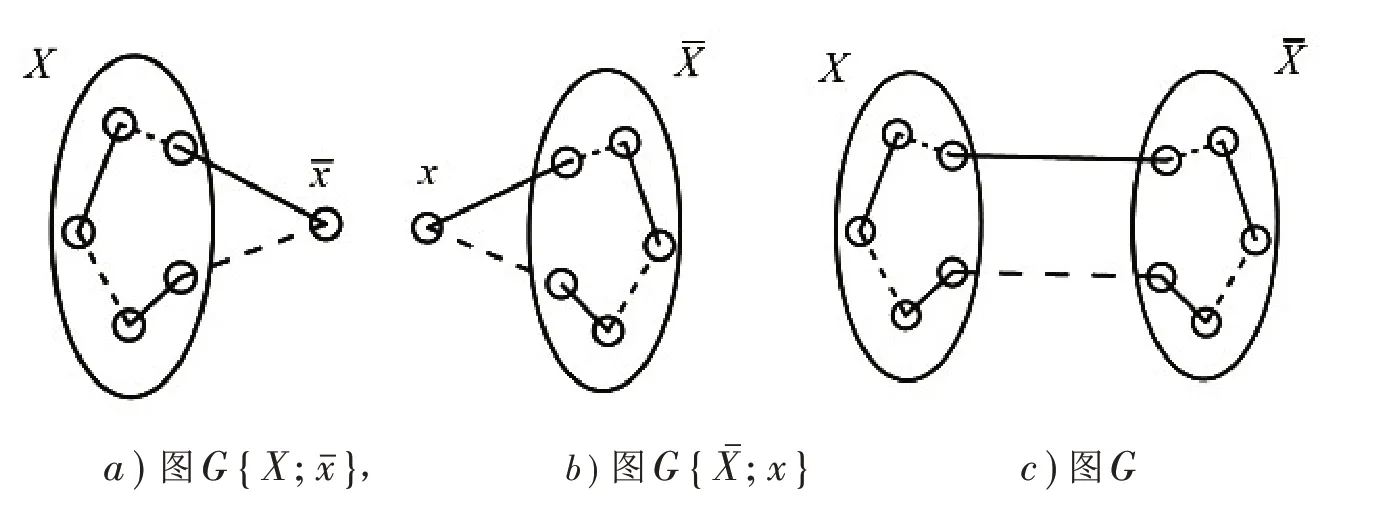
图1 交错图Fig.1 Intercaced graph

情况2|M1⋂C|=a≥3,其中a为奇数,|M2⋂C|= 1.

记{e} =M2⋂C.在这种情况下,我们断言M1ΔM2形成唯一个交错圈C1.否则,M1ΔM2还会还包含另一个圈C2,下面将分情况证明圈C2存在性的矛盾.

情况2.1 若|C2⋂(M1⋂C)|＜a−1,令M3=M1ΔC2,则M3也为图G的一个完美匹配.此时M3至少包含M1⋂C中的两条边，故|C⋂M3|≥2.这时图G存在两个完美匹配M1和M3,它们与robust割C的交的基数都大于1,与引理3矛盾.

故此时只需考虑|C2⋂(M1⋂C)|≥a−1 的情况,即|C2⋂(M1⋂C)|=a−1 和|C2⋂(M1⋂C)|=a的情况.

情况2.2 当|C2⋂(M1⋂C)|=a−1时,此时有两种情况.

1）{e} ∈M1⋂C,即M1⋂M2⋂C={e}.

此时,|(M1ΔM2)⋂C|=a−1,即由M1ΔM2形成的若干圈只与robust割C中的a−1 条边为公共边,而圈C2满足|C2⋂(M1⋂C)|=a−1,故此时圈C1只能满足|C1⋂C|= 0,也即有|C1⋂(M1⋂C)|＜a−1.可完全类似情况2.1进 行处理，进而产生矛盾.

2）{e} ∉M1⋂C,即M1⋂M2⋂C=∅.

在此情况下,由于|C2⋂(M1⋂C)|=a−1,由引理5，必存在另一个交错圈C3,它包含e和M1⋂C的某一边.令M4=M1ΔC3,则M4也是图G一个完美匹配,且|M4⋂C|=a≥3,故此时又找到了两个G中的完美匹配M1和M4,它们与robust割C交的基数都大于1,与引理3产生矛盾.

情况2.3 当|C2⋂(M1⋂C)|=a时,由于a为奇数,根据引理5，必有C2⋂(M2⋂C)={e} ,即C2包含C⋂(M1⋃M2)中的所有边,从而C1⋂C=∅.也即有|C1⋂(M1⋂C)|＜a−1,同样可以归结为情况2.1 进行处理矛盾.

结合情况1 和2 的分析,可得∀M1,M2∈ℳ(G).M1ΔM2形成唯一交错圈,符合PM紧邻定义.故图G是PM紧邻的,定理得证.