分数阶微分方程边值问题解的存在性和唯一性

吴怡敏

（闽南师范大学数学与统计学院，福建漳州363000）

分数阶微分方程在自动控制、航天技术、信号识别、生物数学、物理学、力学等领域应用广泛[1-3].相比于整数阶导数,分数阶导数为描述过程的记忆性和遗传性提供了极好的工具[4].方程中含有函数p(t),会给研究工作带来一定的困难.文献[5]中给出并证明了几类含p(t)项的整数阶微分方程解的存在性和唯一性,但对于含p(t)项的分数阶脉冲微分方程解的研究还未给出.受文献[5]启发,构造如下Riemann−Liouville分数阶脉冲微分方程：

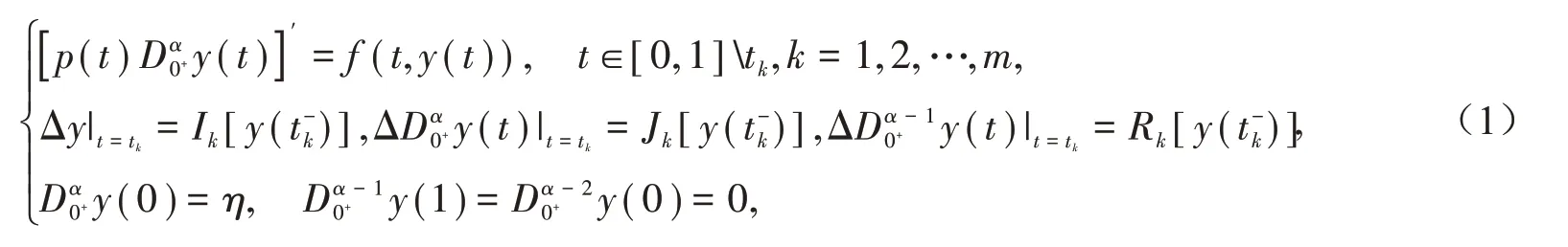
其中,是保持下限为0 不变的Riemann−Liouville分数阶导数；1 ＜α＜2；(t,y(t))∈Ω,Ω =[0，1]×R;f∈C[Ω,R]⋂L1[Ω,R];η∈R;其中是2 −α阶的R−L型分数阶积分；J=[0,1],0 =t0＜t1＜…＜tm+1=1;Ik、Jk、Rk∈C(R,R),k=1,2,…,m;p(t)∈C1(J,R+)；Δy|t=tk=y(t+k)−y(t−k),y(t+k)和y(t−k)分别是y(tk)的右极限和左极限,且y(t−k)=y(tk),此外和也有类似的定义.

1 预备知识

引理1[1]设[a,b](−∞＜a＜b＜+∞)是R上的有限区间,那么α∈R+阶Riemann−Liouville分数阶积分定义为：

其中,Γ(α)为Gamma函数,右端积分在R+(R+={x|x＞0,x∈R})上逐点有定义.当a=0时,一般省略下标,记为Iα.

引理2[1]函数f:[a,+∞)→R的α∈R+阶Riemann−Liouville分数阶导数定义为：

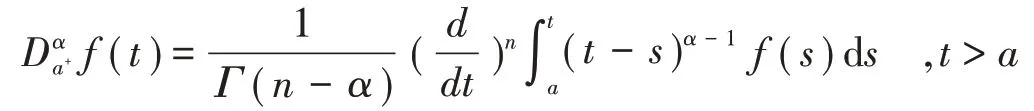
其中,当α≠N+时,n=[α+1],[α]表示α的整数部分；当α=N+时,n=α.右端在R+上逐点有定义.

引理3[2]设α＞0,如果f∈L1([a,b],RN)且In−α f∈ACn([a,b],RN),那么等式

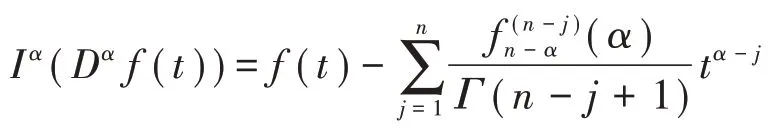
在[a,b]上几乎处处成立,其中n是大于或等于α的最小整数.

2 主要结果

考虑分段连续函数空间PC(J,R)={y:J→R|y(t)在t≠tk处连续,t=tk处左连续};PC(J,R)是Banach空间,范数记PC∂(J,R)={y:D∂0+y(t)∈PC(J,R)}(∂=α,α−1)，赋范数‖y‖PC∂=显然,PC∂(J,R)是Banach空间.

引理4[3]如果α＞0,β＞0,那么

引理5设y∈PC2(J,R)，I2−αy∈AC2(J,R)且1 ＜α＜2,那么是式（1）的解当且仅当

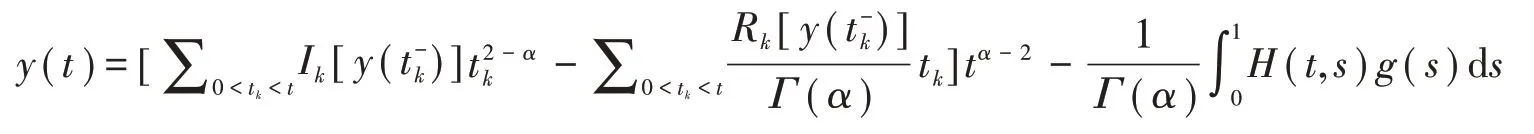
其中

引理6假设：

定义算子T:PC[J,R]→PC[J,R]，且则T是全连续算子.

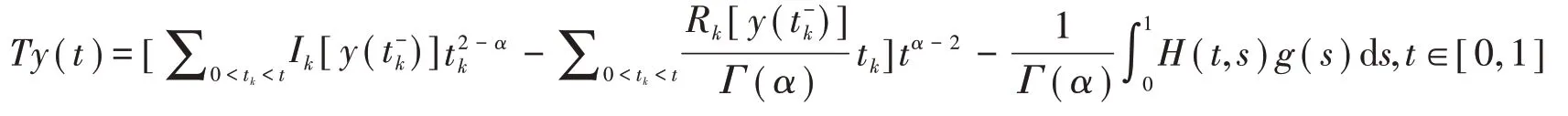
证明i)由f、Jk、p(s)的连续性知g(s)连续,由Ik、Rk、H连续得Ty连续.

ii)对∀λ＞0,令Bλ={y∈PC(J,R):‖y‖≤λ}.那么对∀y∈Bλ,t∈[0,1],有|g(s)|≤d，其中则，故T(Bλ)一致有界.

iii)对∀y∈Bλ,t1,t2∈[0,1]且t1＜t2，则|显然当t1→t2时,不等式右端趋于0,即(Ty)(t1)→(Ty)(t2),故T(Bλ)为等度连续集.由Arzele−ascoli定理知,T全连续.

定理1对引理6中的定义的有界集

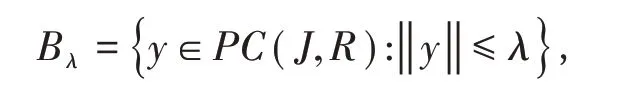
记M(β,θ,γ)=[γa+(βΓ(α+1)+θα)p0b],当时,式（1）在[0,1]上至少有一个解.

证明由于易知‖Ty(t)‖≤λ,故T(Bλ)是PC(J,R)中的一个列紧子集,由Schauder不动点定理知T在[0,1]中至少存在一个不动点y∈Bλ，因此式（1）在[0,1]上至少有一个解y∈Bλ.

定理2假设：

1)Ik、Jk、Rk满足

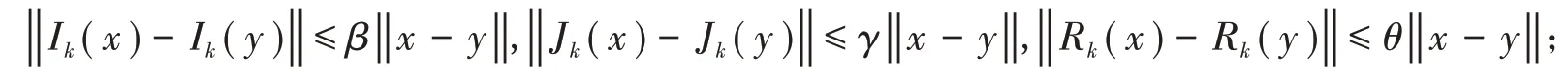
2)‖f(t,x)−f(t,y)‖≤M1‖x−y‖

证明对∀x,y∈PC(J,R),有

由条件知上式满足Banach压缩映像原理,T在PC(J,R)上存在唯一不动点，故式（1）在[0,1]上有唯一解.

3 实例

例1考虑如下分数阶脉冲微分方程边值问题：

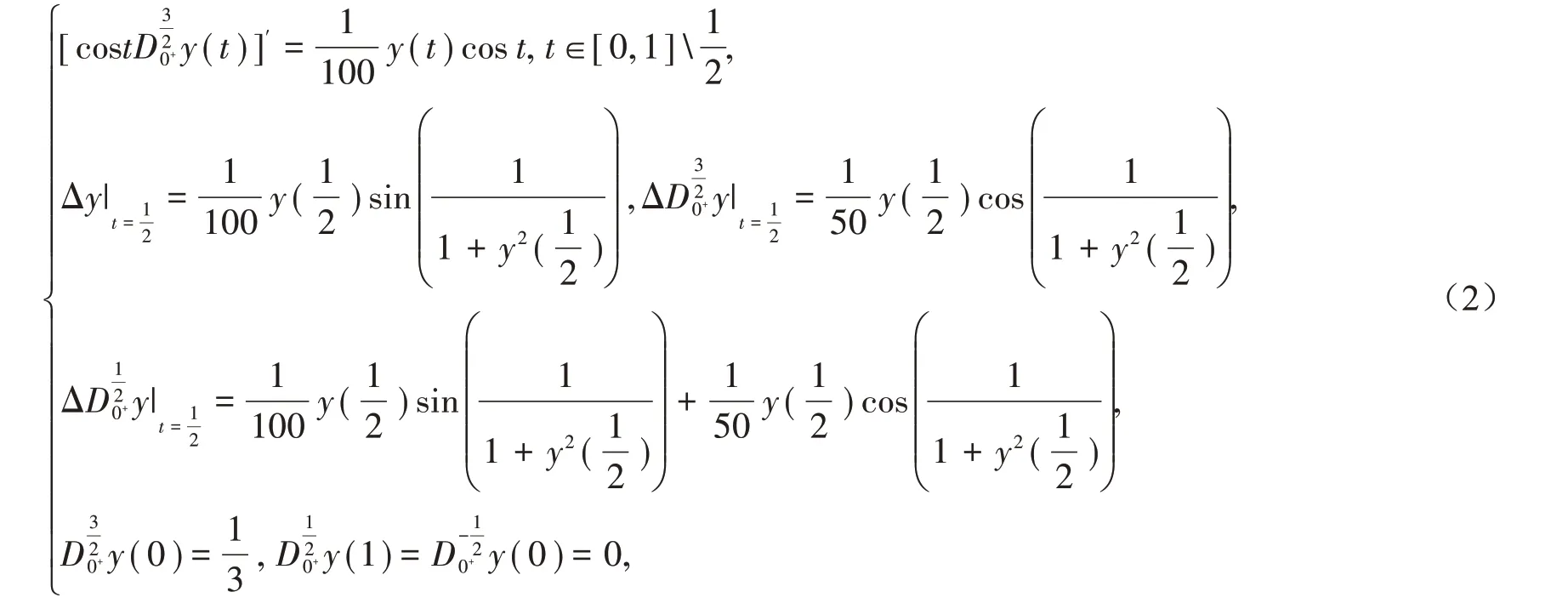
证明由于故且满足引理6的条件,当0.846时满足定理1 的条件,故式（2）在[0,1]中至少存在一个解.显然式（2）满足条件定理2 的条件，且故由定理2知式（2）在[0,1]存在唯一的解.