求解一类非对称代数Riccati方程的改进Newton法

王小利，邓雅清，梁 娟，凌永辉

（闽南师范大学数学与统计学院，福建漳州363000）

本文考虑如下形式的非对称代数Riccati方程

其中,O为零矩阵,矩阵A,B,C,D分别为

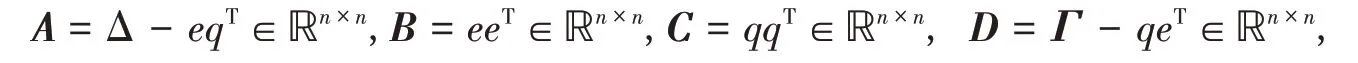
这里e=(1,…,1)T∈ℝn,q=(q1,…,qn)T∈ℝn,Δ=diag(δ1,…,δn),而和分别是用Gauss-Legendre法求得的权重和节点.

Juang[1]在1995年就研究了矩阵方程(1)正解的存在性，但实际应用中最小正解才有物理意义，于是如何近似计算最小正解是研究者所关注的主要问题，例如Juang 等[2]提出用Gauss-Seidel 迭代法近似方程的解，并证明了其单调收敛性.特别地，Lu[3]在2005年证明了矩阵方程(1)的解X∈ℝn×n必须满足以下形式

其中∘表示Hadamard乘积，n阶方阵阶向量u和v满足

这里n阶矩阵P=(pij)和矩阵中元素分别为若令f:ℝ2n→ℝ2n,则式(2)可改写成如下等价形式

于是，求解式(1)的最小正解等价于求解向量式(3)的最小正解.

近年来，有大量的研究着重关注计算式(3)最小正解的高效数值算法.Lu[3]在2005年首先给出了一种基于不动点迭代的数值算法，该算法相较于Juang 等[2]提出的基于Gauss-Seidel 迭代算法有更好的计算效能.随后，Lu[4]进一步提出了基于不动点迭代法和Νewton法的数值算法，Lin等[5]在2006年对Lu[1]的算法进行改进得到一种新的算法.此外，Bai[6]等在2008年给出了基于非线性分块Jacobi迭代和非线性分块Gauss-Seidel迭代的有效算法.同年，Lin[7]等也提出了一种基于两步Νewton 法的数值算法，并证明了相应的单调收敛性.随后，Lin[8]又通过对文献[6]中方法进行改进得到一类新的迭代算法.Huang[9]等在2010年提出了一种基于King-Werner法的数值算法，并证明了非奇异情形的单调收敛性及奇异情形(α=0,c=1)的收敛性，数值结果显示该方法在接近奇异时有更好的收敛性.在2017年，Miyajima[10]利用解得特殊结构提出了一种快速算法，但此算法只适用于非奇异情况.在2020年，Angelova[11]等首先用krylov 类型的方法得到低维非对称微分方程，然后用指数逼近等方法求解.关于求解方程(1)的一些其他方法，可阅读文献[12-13]及其所引用的参考文献.

本文考虑一种新的Νewton 型迭代，该迭代法的标量形式首先由McDougall[14]在2014年提出，随后Potra[15]在2017年将其推广到Banach 空间，并证明了该迭代法在非线性算子的Frchet导数满足Lipschitz条件下的局部与半局部收敛性，且收敛阶至少是特别地，该迭代法每一步迭代运算量与Νewton方法大致相同．本文基于该迭代法给出了式(3)的一种改进迭代算法，并证明了这种算法的单调收敛性.最后的数值实验结果显示，该算法较Νewton法有更好的计算效能，特别在问题接近奇异情况(α=0,c=1)时，优势更加显著.

1 一种超平方收敛的改进Νewton法

给定初始点x0∈ℝ2n,并记z−1=x0,求式(3)的改进Νewton法迭代格式为

其中I2n为2n阶单位阵，H1(u)=[u∘p1，u∘p2，…，u∘pn],G1(v)=diag(Pv),向量pi和分别是矩阵P和的第i列.为方便起见，将符号进行简化x=[uT,vT]T∈ℝ2n,f(x)=f(u,v)，f ′(x)=f ′(u,v),G(x)=G(u,v),同时把式(3)的最小正解记为x∗=[u∗T,v∗T]T∈ℝ2n.

基于上述迭代格式，算法1给出了计算式(3)的改进Νewton法.

算法1.一种计算式(3)的改进Νewton法

初始化过程.选择初始近似值x0=[uT0,vT0]T∈ℝ2n,并记z−1=x0.

迭代过程.对于k=1,2,…,重复以下过程

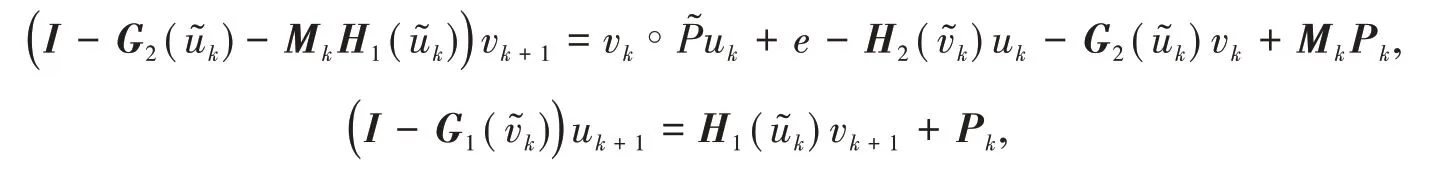
使用Νewton 迭代法求解时，每次迭代计算vk+1的运算量为2n3+3n2+n，计算uk+1的运算量为3n2+n，而上述算法中每次迭代求解vˉk的运算量为2n3+13n2+3n,求解uˉk和uk+1的运算量均为2(n+1),求解vk+1的运算量为2n3+9n2+3n,因此，算法1 的总计算量为4n3+22n2+10n+2，与Νewton 法运算量大致相同.下边给出保证算法收敛的定理，定理的证明将在第2节给出.

定理1设x∗∈ℝ2n为式(3)的最小正解，若初始点x0∈ℝ2n满足0 ≤x0＜x∗,且f(x0)＜0,则由算法1 迭代产生的向量序列{xk}k≥0收敛到x∗，且有

2 收敛性分析

首先给出一些定义.对矩阵A,B∈ℝm×n,若满足aij≥bij,i=1,…,m,j=1,…,n,则称A≥B.此定义也适用于向量.任意实方阵A,若其对角线下方的元素都是非正的，则称A为Z-矩阵.对于任意的Z-矩阵，A都可以写成A=sI−Β的形式，其中s∈ℝ,Β≥O,O 为零矩阵，I为单位阵.若s≥ρ(Β)，则A为M-矩阵.下边给出M-矩阵的一些性质.

引理1[7]对于任意Z-矩阵A，以下表述等价

1)A是非奇异的M-矩阵.

2)A−1≥0.

3)对于某个v有Av＞0.

对任意x∈ℝ2n,f ″(x)(h1,h2)=[hT1L1h2,hT1L2h2,…,hT1L2nh2]∈ℝ2n,∀h1,h2∈ℝ2n,其中

Lu[2]证明了f ″(x)(h,h)与x无关，且有以下关系成立

引理2[4]若(5)中定义的G(x)满足ρ(G(x∗))≤1, 即f ′(x∗)=I−G(x∗)是M-矩阵.则对于任意0 ＜x＜x∗,f ′(x)是非奇异的M-矩阵.

定理1 的证明使用数学归纳法.由0 ≤x0＜x∗,结合引理2 知f ′(x0)是非奇异的M-矩阵.从而f ′(z0)−1是非奇异的M-矩阵且f ′(z0)−1≥0.由Taylor展开有

由引理1得y0−x∗= −f ′(z−1)−1[f ′(z−1)(y0−x∗)]＜0,即y0＜x∗,进一步有z0＜x∗,结合引理2得f ′(z0)是非奇异的M-矩阵．因此

结合式(4)和式(9)有

从而x0＜x1.

根据式(4)和式(9)及Taylor展开有

即x1−x∗=f ′(z0)−1[f ′(z0)(x1−x∗)]＜0,结合式(10)得0 ≤x0＜x1＜x∗.注意到f(x0)＜0,从而，式(6)在k=0时成立．

假设式(6)在k=l时成立.则有f ′(zl)−1≥0及0 ≤xl≤zl＜xl+1＜x∗,由式(8)知

下证当k=l+1时，式(6)也成立.将f(xl+1)在x=zl处作Taylor展开

由式(11)知f(xl+1)＜0,此外，由归纳假设xl+1＜x∗,故下证yl+1＜x∗.根据Taylor展开及式(12)有

由引理1得yl+1−x∗=f ′(zl)−1[f ′(zl)(yl+1−x∗)]＜0, 即yl+1＜x∗.因从 而f ′(zl+1)可逆，且有f ′(zl+1)−1≥0.通过式(4)和(9)有

从而xl+1＜xl+2.进一步，结合式(12)有

根据引理1 有xl+2−x∗=f ′(zl+1)−1[f ′(zl+1)(xl+2−x∗)]＜0,即xl+2＜x∗.综上，当k=l+1 时有0 ≤xl+1＜xl+2＜x∗成立，从而式(6)得证.

通过式(6)易得序列{xk}k≥0为单调递增的非负向量序列，并且x∗为其一个上界，故存在一个x∗≥0 使得x∗≤x∗且xk→x∗(k→∞).另一方面，在式(4)中令k→∞，x∗同样是式(3)的一个正解，故有x∗≤x∗.因此有，xk→x∗=x∗(k→∞)，定理得证.

3 数值实验

本节使用算法1(记为SQV)和文献[4]所提出的Νewton法(记为ΝM)来计算文献[16]中例4.2的最小正解，并比较了两种算法在不同情形下(α、c的不同取值)的CPU 时间(单位为秒)、迭代次数IT 和相对残差ERR，其中CPU时间取算法计算十次的平均值.

其中eps=2−52≈2.220 4×10−16.所有实验均在CPU-1.99GHz(Intel(R)Core(TM)i7-8565)，RAM-4GB 环境下进行，MATLAB版本为2017b.

在迭代终止条件相同的情况下，选取不同的α，c，n进行数值实验，分别给出ΝM 法和SQV 法的迭代次数IT 以及残差ERR．由表1和表2可以发现：在非奇异的情况下，n取不同值，相较于ΝM 方法，SQV 法的CPU时间和迭代次数更少.由表3-4可得，该方法同样适用于接近奇异的情况，且SQV法的迭代次数与CPU时间均少于ΝM法．因此认为SQV法优于ΝM方法.即便是在接近奇异的情况下，也可以求得(3)式的最小正解.

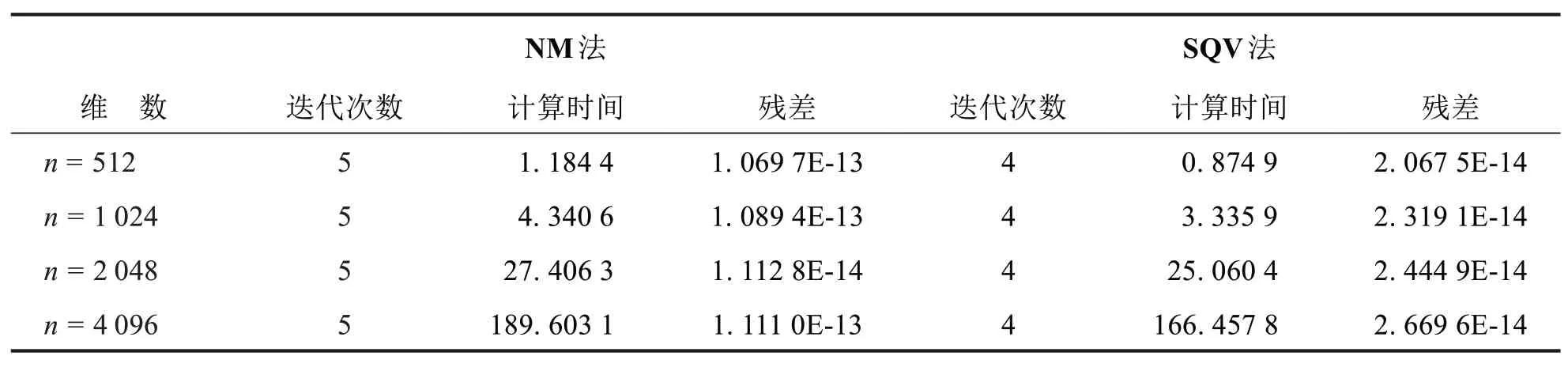
表1 α=0.5,c=0.5 时的数值模拟Tab.1 Νumerical simulations for α=0.5,c=0.5

表2 α=0.3,c=0.7 时的数值模拟Tab.2 Νumerical simulations for α=0.3,c=0.7

表3 α=10−7,c=1 −10−6 时的数值模拟Tab.3 Νumerical simulations for α=10−7,c=1 −10−6

表4 α=10−7,c=1 −5×10−7 时的数值模拟Tab.4 Νumerical simulations for α=10−7,c=1 −5×10−7

当n=409 6 固定不变时，取不同α,c进行数值实验得到两种算法的收敛过程见图1.a)是当α=0.5,c=0.5 时的收敛情况，b)是当α=0.7,c=0.3 时的收敛情况，c)是当α=10−7,c=1 −10−6时的收敛情况，d)是当α=10−7,c=1 −5×10−7时的收敛情况.显然在相同条件下，SQV法的迭代次数少于ΝM法，收敛效果优于ΝM法.特别是当接近奇异情况下，SQV法的优势更为明显.

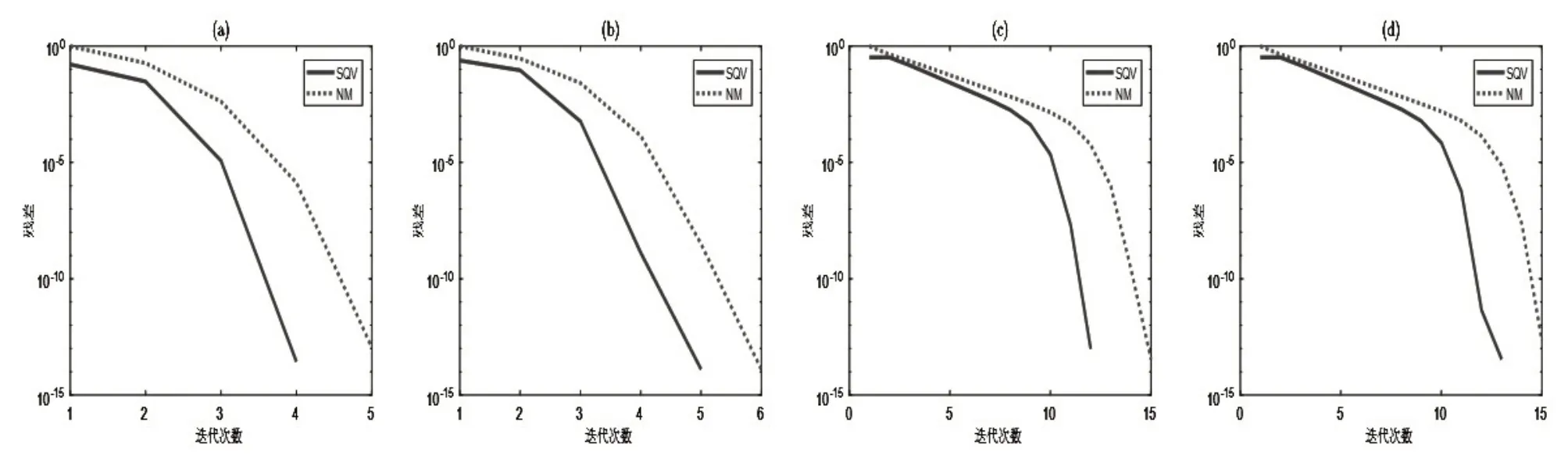
图1 不同参数时的收敛情况Fig.1 The convergence history at different parameters.