组合梁疲劳后的刚度退化规律及计算模型

2021-03-31刘小玲

振动与冲击 2021年6期

汪炳，黄侨，刘小玲

(1.宁波大学土木与环境工程学院，浙江宁波 315211；2.东南大学交通学院，南京 210096；3.宁波大学海运学院，浙江宁波 315211)

钢-混凝土组合梁以其自身的优点和特点在公路桥梁、城市桥梁及铁路桥梁中得到了广泛的应用[1]。然而在车辆等疲劳荷载作用下，组合梁内部容易出现疲劳损伤，严重危害桥梁结构的安全性与耐久性[2]。众所周知，结构的疲劳损伤会随着疲劳加载次数的增加而不断累积，导致结构刚度和承载力的不断退化。一旦这种损伤累积至一定程度后，结构将发生突然失效或破坏，造成重大的人员伤亡或财产损失[3]。因此，掌握组合梁在疲劳荷载作用下损伤累积和性能退化的规律，特别是通过梁体本身的若干力学性能指标对组合梁的疲劳性能退化程度作整体把控尤为重要。

梁的刚度是反映组合梁疲劳性能退化的重要指标之一，且刚度测试往往简单易实现[4]。探索组合梁在疲劳荷载作用下的剩余刚度退化规律对于掌握组合梁服役期间不同阶段的使用性能具有重要意义。迄今为止，各国学者在组合梁疲劳性能方面开展了广泛的试验研究：Hanswille等[5]通过大量推出试验研究发现，栓钉大约在10%～20%的疲劳寿命时就出现了早期裂纹，这是导致其疲劳后静力强度降低的主要原因；汪炳等[6]总结了以往学者27组栓钉剩余强度推出试验数据，建立了栓钉连接件疲劳后剩余承载力退化模型；李小珍等[7]基于3根钢-混凝土组合梁的疲劳试验，提出以栓钉剪切破坏为表征将组合梁在疲劳下的损伤划分为3个阶段。同时也有部分学者试验结果表明了组合梁在疲劳荷载作用下梁体刚度退化的现象，如刘小洁等[8]和杨涛等[9]的试验结果均表明组合梁在疲劳荷载作用下刚度发生了明显的退化。但目前仍没有学者提出在疲劳作用下适用于组合梁刚度退化规律的计算分析模型。

本文选取带栓钉连接件的钢-混凝土组合梁为研究对象，选取6根栓钉试验梁分别进行静力、疲劳和部分疲劳试验，观察不同疲劳加载次数下梁的刚度、变形、滑移等力学性能变化特征，分析刚度退化的主要影响因素，在此基础上通过参数拟合得到组合梁剩余刚度随疲劳加载次数的退化规律计算模型并验证。该研究成果为组合梁疲劳荷载作用后刚度退化模型的建立提供了一种思路和方法。

1 试验设计

1.1 试件尺寸

本次试验共设计了6个栓钉组合梁试件，按完全抗剪连接设计[10]，钢梁材料等级为Q345，混凝土材料强度等级为C50，栓钉型号为Φ13×60 mm，材料为ML-15，组合梁试件的尺寸构造及栓钉布置情况如图1所示。

图1 试验组合梁尺寸及构造(mm)Fig.1 The size and construction of composite beams specimens (mm)

在试验之前，测试了组成组合梁试件的相关材料强度。试验测得钢梁的弹性模量为2.06×105MPa，屈服强度为352 MPa；混凝土的立方体强度为59.7 MPa，弹性模量为3.59×104MPa；栓钉的弹性模量为2.0×105MPa，极限强度为525 MPa。

1.2 试验加载方式

试验梁边界条件为简单支承，采用跨中单点加载，见图2。为了解试验梁在疲劳荷载作用下的刚度退化规律，试验加载内容分为3组：①一个静载破坏试验，试件编号为SCB-1，目的是确定试验梁的静力极限承载力Pu；②一个完全疲劳试验，试件编号为FCB-1，目的是确定试验梁的疲劳寿命N；③4个部分疲劳破坏试验，在完成既定疲劳加载次数后在进行静载破坏。试件编号依次为SFCP-1～SFCP-4，分别在疲劳加载50万次、100万次、150万次、200万次后将其进行静载破坏。疲劳加载具体参数见表1。

表1 试验梁的破坏模式及试验结果Tab.1 Failure modes and test results of test beams

图2 试验梁加载过程及测试设备Fig.2 Loading process of test beam and testing system

需要指出的是，在本次试验梁设计时，主要以组合梁跨中下缘钢梁的疲劳应力幅值作为疲劳加载控制。根据JTG D64—2015《公路钢结构桥梁设计规范》[11]中工字钢梁焊接截面的疲劳细节，200万次疲劳寿命对应的钢梁下缘应力幅值为100 MPa，进而反推出本次试验中疲劳加载幅值的比例为0.25Pu。

2 试验结果

2.1 试件破坏形态

在本次试验中，静载破坏试验梁的整个破坏过程与传统组合梁破坏形式基本一致：在加载初期，整根梁变形协同；随着荷载不断增大，跨中加载区域的混凝土翼板下缘开始出现竖向裂缝，并不断向上延伸；当接近极限荷载时，跨中混凝土翼板压碎剥落，钢筋外露，钢梁也发生较大的屈服变形，最终的破坏模式如图3(a)所示。完全疲劳破坏试验梁在疲劳加载初期，整根梁完好，没有明显的损伤和破坏特征；随着疲劳循环次数的增加，混凝土翼板下缘开始出现细微的竖向裂缝，并缓慢延伸发展；最后达到疲劳寿命时，组合梁中栓钉被剪断，钢梁与混凝土翼板脱开，如图如图3(b)所示。部分疲劳破坏试验梁的破坏形式包含了以上两种形式，表1给出了所有试验梁的破坏模式。

图3 试验梁破坏模式Fig.3 Failure mode of test beams

从表1可以看出，对于部分疲劳破坏试验，试验梁的破坏模式与循环加载次数密切相关，随着加载次数的增加，破坏模式从静载破坏模式逐渐转变成完全疲劳破坏模式。在不断的疲劳荷载作用下，栓钉连接件出现了损伤，这导致组合梁由完全抗剪连接到部分抗剪连接的转变，因此带来了破坏模式的不同。因此组合梁结合面的抗剪连接程度对刚度的性能具有重要影响。

2.2 试验结果分析

2.2.1 荷载-挠度曲线

荷载-挠度曲线可直观反映加载过程中梁式结构刚度、承载力等力学性能的变化状况，在试验中是一项重要测试内容。图4给出了静力破坏和部分疲劳破坏试验梁的荷载-跨中挠度曲线。从图中可以看出，随着疲劳加载次数的增加，组合梁的各项力学性能包括极限承载力、线弹性阶段的刚度以及延性均表现出降低。

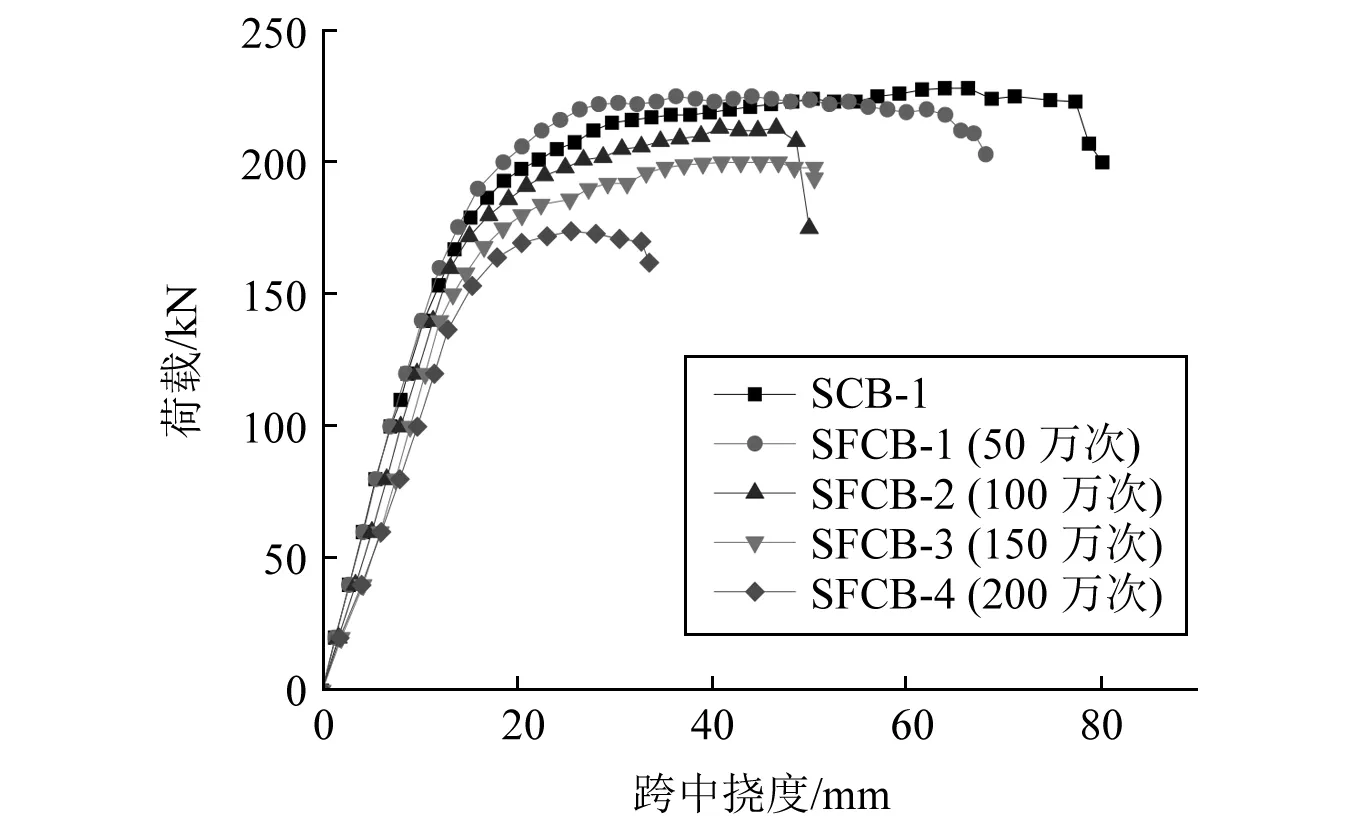
图4 荷载-跨中挠度曲线Fig.4 Load-mid-span deflection curve

为进一步对比不同试验梁之间在不同疲劳加载次数后的剩余刚度退化情况，首先根据材料力学基本原理，利用梁在外荷载条件下的挠曲线方程，可反算得到组合梁的抗弯刚度B表达式

(1)

式中:α为组合梁的挠度系数；M为组合梁跨中截面弯矩；L为组合梁计算跨径；f为组合梁挠度。

由于在本试验中试验梁为跨中集中力加载，边界条件为简单支承，因而可根据式(1)进一步推得在疲劳加载中组合梁随加载次数变化的时变刚度计算公式

(2)

式中:fn为每次加载到疲劳上限时的挠度;P为与挠度fn相对应的荷载，即P=Pmax=0.6Pu=136 kN。

图5给出了不同次数疲劳循环作用后试验梁SCB-1与SFCB-1～SFCB-4剩余静力刚度的对比。

从图5中可知，随疲劳加载次数的增加，试验梁剩余静力刚度大体呈下降趋势，且下降幅度较大，如试验梁SFCB-4在经历了200万次疲劳加载之后，其剩余刚度较SCB-1下降了26.7%。这里需要指出的是，试验梁SFCB-1的刚度在疲劳加载50万次后较SCB-1反而提高了1.8%，这可能是由于该试件疲劳加载次数较少，而导致其他影响因素(设备测量误差、试件加工误差、材料不均匀等)“掩盖”了试验梁SFCB-1本就不显著的刚度退化情况。

图5 疲劳循环后剩余静力刚度Fig.5 Residual static stiffness after fatigue cyclic loading

2.2.2 残余挠度

在试验梁疲劳加载过程中，当经历了一次循环次数后，停机卸载进行一次试验梁的挠度测量，此时将梁体不可恢复的挠度定义为试验梁的残余挠度。试验梁的残余挠度可认为是其刚度退化的直观表达，因其直接反映了试验梁内部的损伤发展情况[12]。图6给出了5个试验梁跨中残余挠度的变化曲线。

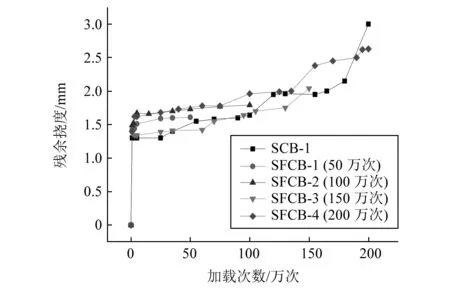
图6 跨中残余挠度增长曲线Fig.6 Residual mid-span deflection growth curve

由图6可知，试验梁的残余挠度变化呈典型的三个阶段变化，分别是极速增长阶段、平稳增长阶段以及快速增长阶段。具体来看，在疲劳加载初期，残余挠度极速增长，各片试验梁的挠度增长值均达到1.2 mm以上，究其原因可能是因加载初期钢梁、混凝土板以及栓钉之间接触不密实，存在塑性压缩所致。第二阶段为平稳增长期，在此阶段试验梁的残余挠度平稳且缓慢增长。第三阶段为在疲劳加载次数接近于梁疲劳寿命时，梁的残余挠度再次快速增长。试验梁SFCB-1～SFCB-3加载次数未达其疲劳寿命，因此仅表现出两阶段。

2.2.3 相对滑移

相对滑移的大小是反映组合梁组合效果的重要指标，同时也影响梁整体刚度变化的一大因素。在疲劳荷载作用下，相对滑移量也如残余挠度一样会不断累积，累积增长情况也和残余挠度较为一致，呈现明显的三阶段特征，如图7所示。

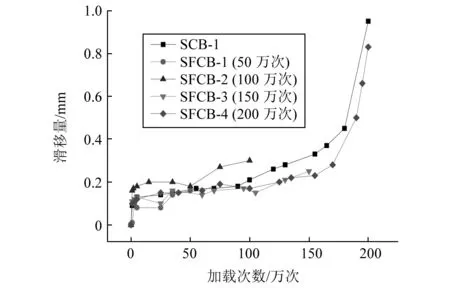
图7 试验梁相对滑移增长曲线Fig.7 Relative slip growth curve of test beam

2.2.4 疲劳过程刚度退化情况

为进一步分析各试验梁在疲劳加载过程中刚度的退化情况，由式(2)计算了试验梁FCB-1及SFCB-1～SFCB-4在不同循环次数下对应的组合梁刚度值，如图8所示。

由图8可知，所有试验梁的刚度均随着疲劳加载次数的增加而退化，且大致退化规律较为一致，呈现为“S”型。当加载至200万次时，试验梁SFCB-4和FCB-1的刚度仅为初始的73.8%和76.2%，退化程度明显。需要指出的是，每根试验梁的初始刚度略有不同，这是试验梁制作过程及试验过程引起的误差造成的，不过基本稳定在8 MN·m2左右。

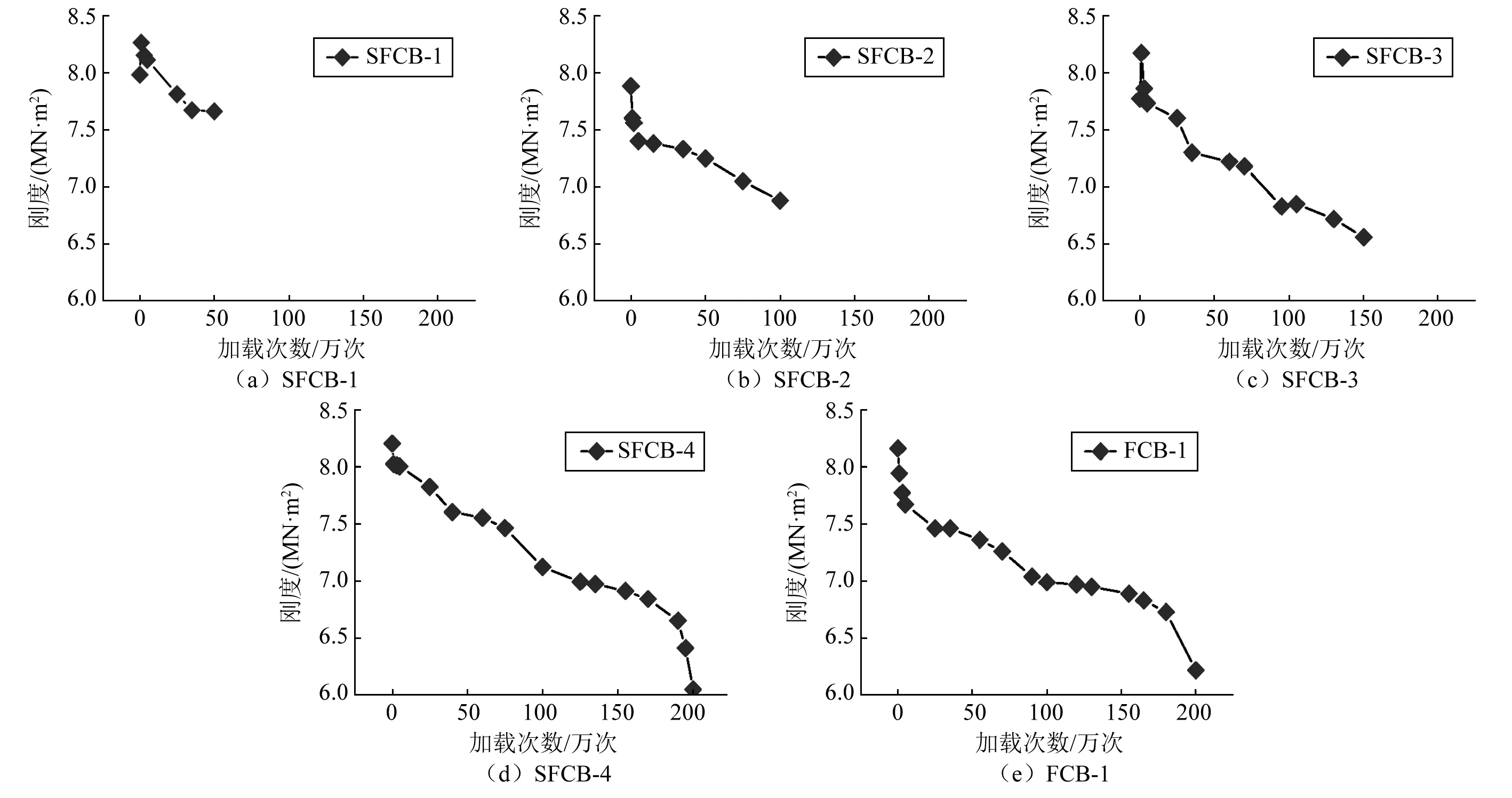
图8 SFCB-1～SFCB-4与FCB-1刚度退化规律Fig.8 Residual stiffness change rules of SFCB-1-SFCB-4 and FCB-1

另外，将每根试验梁的刚度退化情况与上一节中的残余挠度、相对滑移增长之间作了相关性分析，分析结果列于表2。

表2 试验梁刚度与残余挠度、相对滑移相关性分析Tab.2 Correlation analysis of stiffness,residual deflection and relative slip of test beam

由表2可知，试验梁的刚度与残余挠度、相对滑移之间存在的较强的负相关性，尤其是疲劳加载次数较多的试验梁，如FCB-1和SFCB-4，其相关性系数均小于-0.8，甚至达到-0.92，表现出了极强的负相关性。残余挠度的增长体现了组合梁内部的疲劳损伤，这种损伤包括钢梁与混凝土的材料损伤，栓钉连接件的损伤等。而相对滑移的增长则主要体现了组合梁抗剪连接程度的弱化。由此可知，在疲劳荷载作用下，组合梁整体刚度退化的影响因素是多方面的，刚度退化实际上是材料疲劳损伤和抗剪连接程度退化的宏观表现。

3 疲劳荷载作用下组合梁刚度退化规律

由前文分析可知，组合梁疲劳后的刚度退化是组合梁整体发生疲劳损伤的宏观表现，从细观层面来看，这种退化是由混凝土、钢梁材料的损伤退化，栓钉连接件的损伤退化等原因导致的，已有学者通过混凝土[13]、钢材[14]的疲劳后剩余强度试验表明它们在疲劳荷载作用下材料强度呈“先慢后快”的非线性退化。但在组合梁中这些构件的受力状况并不单一，材料之间的损伤联系也十分复杂，因而本文采取的方法是将组合梁看成一个整体，通过梁体的整体刚度的变化来直接表征组合梁的疲劳损伤程度。

3.1 组合梁剩余刚度退化表征

组合梁的剩余刚度退化模型可参考材料剩余强度退化模型的一般公式，即

(3)

式中：B0为组合梁初始刚度；BN为组合梁疲劳破坏时的最终刚度，则整个疲劳过程刚度退化量为(B0-BN)；ζ(n/N)为一个与疲劳寿命比有关的刚度退化函数。

参数B0和BN均可通过试验测量挠度计算得到，因而最关键是要确定刚度退化函数ζ(n/N)。

3.2 刚度退化函数

根据文献研究成果[15-16]，刚度退化函数一般满足三点：在曲线的起点n=0，梁的刚度为初始刚度B0；在曲线的终点n=N，梁的刚度为组合梁疲劳破坏时的最终刚度BN；在曲线的变化过程中，根据试验结果表现，前期应稳定退化，后期加速退化。

为了满足以上三条要求，笔者参考文献[17-18]中的函数，如下所示

(4)

式中，u和v为待定参数。

在确定刚度退化函数后，只需将式(4)代入式(3)中，即可得到组合梁随疲劳加载次数变化的刚度计算公式

(5)

由此可知，式(5)中仅有u和v为不确定参数，只需要通过一系列试验数据对上式进行双参数拟合，即可得到最终的组合梁刚度计算公式。

3.3 组合梁刚度退化模型的建立与验证

根据试验梁FCB-1的疲劳破坏试验进行式(5)拟合，梁的初始刚度B0=8.16 MN·m2。需要说明的是，其疲劳寿命为207.56万次，由于无法测得当时刚度，以200万次测得的刚度作为最终值，BN=6.22 MN·m2。图9给出了拟合结果，可以看出拟合结果较好，拟合优度R2为0.959。而拟合的参数u，v分别为0.439和0.657。

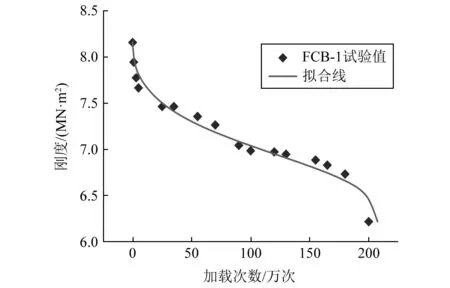
图9 试验梁FCB-1刚度退化拟合曲线Fig.9 Stiffness deterioration fitting curve of FCB-1 test beam

将所有参数代入式(5)，我们得到基于本文所建组合梁的刚度退化计算公式如下

(6)

为验证式(6)的正确性，将其应用到同一批相同疲劳加载方式的试验梁SFCB-1～SFCB-4上，计算值与试验值的对比结果如图10所示。由图可知，4根试验梁的试验值与本文所建立模型的计算值均吻合良好，两者之间的相对误差基本都在±5%以内，个别点误差超过了5%，但也在8%之内。由此验证了本文提出的刚度退化公式的正确性和合理性。然而事实上，本文所提的刚度退化模型仅适用于荷载状态相同的同一批组合梁，当梁的整体尺寸、材料强度、疲劳参数发生变化时，该模型或不再适用。但仍然可以根据本文所提刚度模型建立的方法和思路，通过少量疲劳试验对刚度退化模型进行参数拟合，得到同一批组合梁的刚度退化计算公式。